Расстояние от прямой до параллельной плоскости

В этой статье дано определение расстояния между параллельными прямой и плоскостью, приведена теория, необходимая для нахождения расстояния между прямой и параллельной ей плоскостью методом координат, а также подробно разобраны решения характерных примеров и задач.

Навигация по странице.

Расстояние между параллельными прямой и плоскостью – определение.

Расстояние между прямой и параллельной ей плоскостью определяется через расстояние от точки до плоскости.

Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

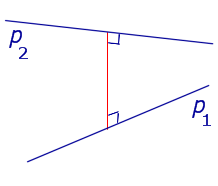
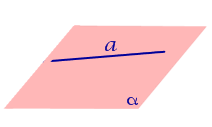
Рассмотрим прямую a и параллельную ей плоскость . Отметим на прямой a точку M₁ и опустим перпендикуляр M₁H₁ из этой точки на плоскость . Длина перпендикуляра M₁H₁ есть расстояние между заданными параллельными прямой и плоскостью.

Озвученное определение расстояния между параллельными прямой и плоскостью тесно связано со следующей теоремой.

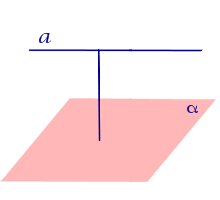
Если прямая a параллельна плоскости , то все точки прямой a равноудалены от плоскости .

Проведем через произвольную точку прямой a плоскость параллельно плоскости . Прямая a при таком построении плоскости лежит в этой плоскости (если бы это было не так, то прямая a пересекала бы плоскость , а, значит, пересекала бы и плоскость в силу параллельности плоскостей и ). В статье расстояние между параллельными плоскостями мы доказали теорему о том, что все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости. Следовательно, все точки прямой a , которая лежит в плоскости , параллельной плоскости , равноудалены от плоскости , что и требовалось доказать.

Нахождение расстояния между прямой и параллельной ей плоскостью – теория, примеры, решения.

Расстояние между параллельными прямой и плоскостью обычно находится с помощью методов, изученных на уроках геометрии в 10-11 классах, — с использованием теоремы Пифагора, признаков равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п.

Когда в трехмерном пространстве введена прямоугольная система координат и требуется вычислить расстояние между заданными параллельными прямой и плоскостью, то применяется метод координат. Сейчас мы его подробно разберем, после чего рассмотрим решения нескольких примеров.

Поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы параллельные прямая a и плоскость , и требуется найти расстояние между прямой a и плоскостью .

Решение этой задачи будем строить на основе определения расстояния между прямой и параллельной ей плоскостью.

Искомое расстояние между заданными параллельными прямой и плоскостью по определению равно расстоянию от точки М₁ , лежащей на прямой a , до плоскости . Если мы определим координаты некоторой точки М₁ , лежащей на прямой a , и получим нормальное уравнение плоскости в виде , то мы сможем вычислить искомое расстояние , применив формулу (эта формула была получена в разделе нахождение расстояния от точки до плоскости).

Итак, алгоритм, позволяющий найти расстояние между параллельными прямой a и плоскостью , таков:

• находим координаты некоторой точки М₁ , лежащей на заданной прямой a (это легко сделать, если знать основные виды уравнений прямой в пространстве);
• получаем нормальное уравнение заданной плоскости вида (для этого нужно знать основные виды уравнения плоскости и при необходимости уметь приводить уравнение плоскости к нормальному виду);
• вычисляем требуемое расстояние между прямой a и параллельной ей плоскостью по формуле .

Воспользуемся полученным алгоритмом при решении задач, в которых требуется вычислить расстояние между параллельными прямой и плоскостью.

Найдите расстояние между параллельными прямой и плоскостью .

Очевидно, точка лежит на прямой, которую определяют канонические уравнения прямой в пространстве .

Получим нормальное уравнение плоскости . Для этого приведем заданное общее уравнение плоскости к нормальному виду: вычисляем нормирующий множитель , умножаем на него обе части заданного общего уравнения плоскости .

Осталось вычислить требуемое расстояние между заданными параллельными прямой и плоскостью как расстояние от точки до плоскости :

Найдите расстояние между прямой и параллельной ей плоскостью .

В рассматриваемой задаче прямая задана уравнениями двух пересекающихся плоскостей. Найдем координаты некоторой точки М₁ , лежащей на этой прямой. Координаты точки М₁ должны удовлетворять уравнениям прямой, то есть, — частное решение системы линейных уравнений . Найдем частное решение этой системы (при необходимости смотрите статью решение систем линейных уравнений). Приняв , приходим к системе уравнений , откуда находим . То есть, имеем .

Теперь получим нормальное уравнение плоскости, которую задает уравнение плоскости в отрезках вида . Для этого переходим к общему уравнению плоскости . Полученное общее уравнение плоскости уже является нормальным уравнением плоскости и его не нужно приводить к нормальному виду.

Осталось вычислить расстояние от точки до плоскости , которое равно искомому расстоянию между параллельными прямой и плоскостью: .

Расстояние между двумя фигурами

Общее определение расстояния между двумя произвольными фигурами выходит за рамки школьной программы, и мы его не приводим. Ряд частных случаев, когда расстояние между двумя фигурами можно ввести на базе школьного материала, перечислен в следующей таблице.

Фигуры	Рисунок	Определение расстояния
Две точки		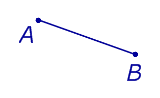Расстоянием между двумя точками называют длину отрезка AB.
Точка, лежащая на прямой		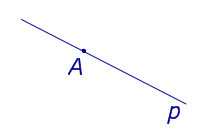Расстояние равно 0.
Точка, не лежащая на прямой		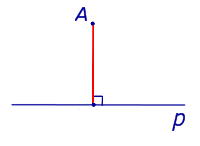Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.
Две параллельные прямые		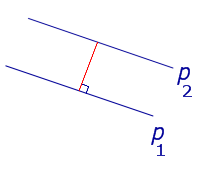Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.
Две пересекающиеся прямые		Расстояние равно 0.
Две скрещивающиеся прямые		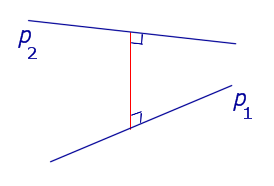Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.
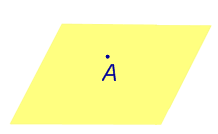
Точка, лежащая на плоскости		Расстояние равно 0.
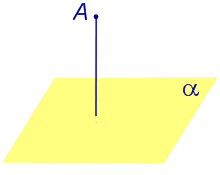
Точка, не лежащая на плоскости		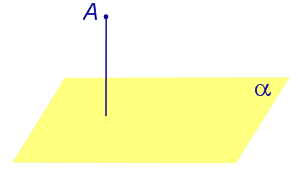Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.
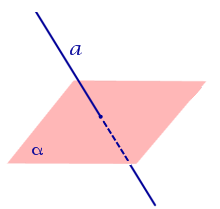
Прямая, пересекающая плоскость		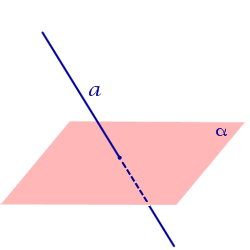Расстояние равно 0.
Прямая, лежащая на плоскости		Расстояние равно 0.
Прямая, параллельная плоскости		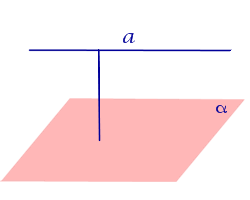Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.
Две пересекающиеся плоскости		Расстояние равно 0.
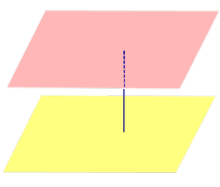
Две параллельные плоскости		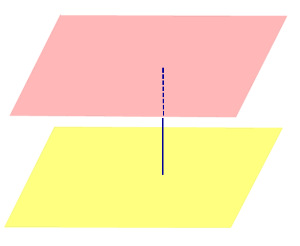Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).
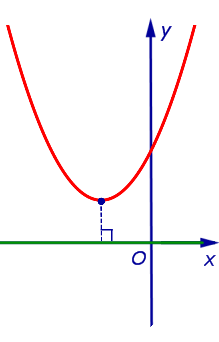
Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс		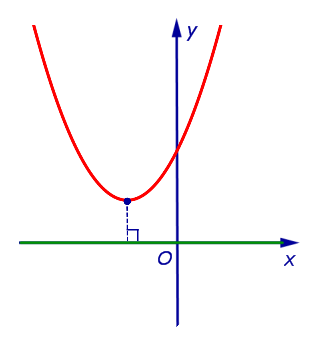Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс. Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.
Окружность и не пересекающая ее прямая		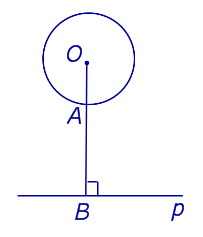Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности, а другой конец – на прямой. Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A, то расстояние от окружности до прямой равно длине отрезка AB.
Две непересекающиеся окружности, каждая из которых лежит вне другой		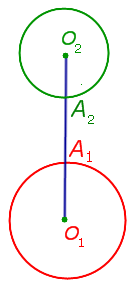Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности , а другой конец – на другой окружности. Если линия центров O1O2 пересекает окружность с центром O1 в точке A1, а окружность с центром O2 – в точке A2, то расстояние между окружностями будет равно длине отрезка A1A2.
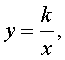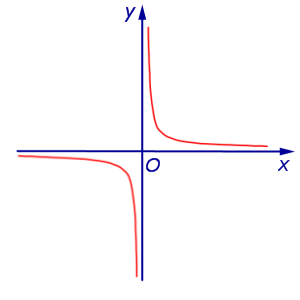Гипербола где k – любое, отличное от нуля, число, и ось абсцисс.		Расстояние между гиперболой и осью абсцисс считается равным 0, поскольку гипербола неограниченно приближается к оси абсцисс (длина отрезка, один из концов которого лежит на гиперболе, а другой конец – на оси абсцисс, может быть сколь угодно малой).

Две точки

Определение расстояния:
Расстоянием между двумя точками называют длину отрезка AB.

Точка, лежащая на прямой

Расстояние равно 0.

Точка, не лежащая на прямой

Определение расстояния:
Расстоянием от точки до прямой называют длину перпендикуляра, опущенного из точки на прямую.

Две параллельные прямые параллельные прямые

Определение расстояния:
Расстоянием между параллельными прямыми называют длину перпендикуляра, опущенного из любой точки одной прямой на другую прямую.

Две пересекающиеся прямые пересекающиеся прямые

Расстояние равно 0.

Определение расстояния:
Расстоянием между скрещивающимися прямыми называют длину общего перпендикуляра к этим прямым.

Точка, лежащая на плоскости

Расстояние равно 0.

Точка, не лежащая на плоскости

Определение расстояния:
Расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из этой точки на плоскость.

Расстояние равно 0.

Расстояние равно 0.

Определение расстояния:
Расстоянием от прямой, параллельной плоскости, до плоскости называют длину перпендикуляра, опущенного из любой точки данной прямой на плоскость.

Две пересекающиеся плоскости

Расстояние равно 0.

Две параллельные плоскости

Определение расстояния:
Расстоянием между параллельными плоскостями называют длину перпендикуляра, опущенного из любой точки одной плоскости на другую плоскость (все такие перпендикуляры имеют одну и ту же длину).

Парабола y = a x 2 + b x + c , не пересекающая ось абсцисс, и ось абсцисс

Определение расстояния:
Расстоянием от параболы, не пересекающей ось абсцисс, до оси абсцисс называют длину кратчайшего отрезка, один из концов которого лежит на параболе, а другой на оси абсцисс.
Этим кратчайшим отрезком является перпендикуляр, опущенный из вершины параболы на ось абсцисс.

Окружность и не пересекающая ее прямая

Определение расстояния:
Расстоянием между окружностью и непереcекающей ее прямой называют длину кратчайшего отрезка, один из концов которого лежит на окружности , а другой конец – на прямой.
Если перпендикуляр OB , опущенный из центра O окружности на прямую, пересекает окружность в точке A , то расстояние от окружности до прямой равно длине отрезка AB.

Две непересекающиеся окружности, каждая из которых лежит вне другой Две непересекающиеся окружности, каждая из которых лежит вне другой

Определение расстояния:
Расстоянием между непересекающимися окружностями называют длину кратчайшего отрезка, один из концов которого лежит на одной окружности, а другой конец – на другой окружности.
Если линия центров O₁O₂ пересекает окружность с центром O₁ в точке A₁, а окружность с центром O₂ – в точке A₂, то расстояние между окружностями будет равно длине отрезка A₁A₂.

Угол между скрещивающимися прямыми и расстояние между ними. Расстояние от точки до плоскости и от прямой до параллельной ей плоскости

Угол между скрещивающимися прямыми и расстояние между ними.
Расстояние от точки до плоскости и от прямой до параллельной ей плоскости

Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.

Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?

Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.

Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях ? и ?. Проведем в плоскости ? прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.

Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.

Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.

Дадим еще два полезных определения.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.

Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.

Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.

📽️ Видео