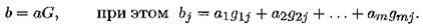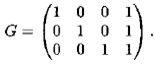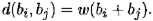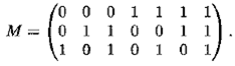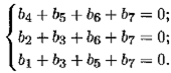Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Раздел создан при поддержке компании
Видео:Хэмминг (15,11) Часть 1Скачать

Код Хэмминга
Будем рассматривать двоичные коды, т.е. упорядоченные наборы (строки) $ (x_1,dots,x_) $ из $ n_ $ чисел $ subset $. Множество таких наборов, рассматриваемое вместе с операцией умножения на константы $ 0_ $ или $ 1_ $ и операцией поразрядного сложения по модулю $ 2_ $: $$ (x_1,dots,x_n)oplus (y_1,dots,y_n)=(x_1oplus y_1 ,dots,x_noplus y_n ) = $$ $$ = (x_1+y_1 pmod,dots,x_n+y_n pmod) $$ образует линейное пространство, которое мы будем обозначать $ mathbb V^n $, а собственно составляющие его наборы будем называть векторами; причем, для определенности, именно векторами-строками. Это пространство состоит из конечного числа векторов: $ operatorname (mathbb V^n)=2^n $.
Видео:Код ХэммингаСкачать

Расстояние Хэмминга
Расстоянием Хэмминга между двумя векторами $ B=(b_1,dots,b_n) $ и $ C=(c_1,dots,c_n) $ из $ mathbb V^n $ называется число разрядов, в которых эти слова отличаются друг от друга; будем обозначать его $ rho(B,C) $.
Доказать, что $ rho(B,C)= displaystyle sum_^n left[ (1-b_j)c_j+ (1-c_j)b_j right] $ .
Весом Хэмминга вектора $ B=(b_1,dots,b_n) $ называется число его отличных от нуля координат, будем обозначать его $ w(B) $. Таким образом 1) $$ w(B)= b_1+dots+b_n, qquad rho(B,C)=|b_1-c_1|+dots+ |b_n-c_n|=w(B-C) . $$
Расстояние Хэмминга является метрикой в пространстве $ mathbb V^n $, т.е. для любых векторов $ subset mathbb V^n $ выполняются свойства
1. $ rho(X_1,X_2) ge 0 $, и $ rho(X_1,X_2) = 0 $ тогда и только тогда, когда $ X_1=X_2 $;
2. $ rho(X_1,X_2) = rho(X_2,X_1) $;
3. $ rho(X_1,X_3)le rho(X_1,X_2)+ rho(X_2,X_3) $ («неравенство треугольника»).
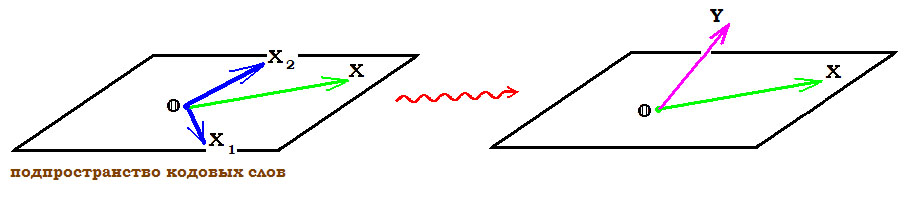
Пусть теперь во множестве $ mathbb V^n $ выбирается произвольное подмножество $ mathbb U $, содержащее $ s_ $ векторов: $ mathbb U= $. Будем считать эти векторы кодовыми словами, т.е. на вход канала связи будем подавать исключительно только эти векторы; само множество $ mathbb U $ будем называть кодом. По прохождении канала связи эти векторы могут зашумляться ошибками. Каждый полученный на выходе вектор будем декодировать в ближайшее (в смысле расстояния Хэмминга) кодовое слово множества $ mathbb U $. Таким образом, «хорошим» кодом — в смысле исправления максимального числа ошибок — может считаться код $ mathbb U $, для которого кодовые слова далеко отстоят друг от друга. С другой стороны, количество кодовых слов $ s_ $ должно быть достаточно велико, чтобы делать использование кода осмысленным; во всяком случае, будем всегда считать $ s>1 $.
Минимальное расстояние между различными кодовыми словами кода $ mathbb U $, т.е. $$ d=min_<subset atop jne k> rho (U_j,U_k) $$ называется кодовым расстоянием кода $ mathbb U $; будем иногда также писать $ d(mathbb U) $.
Теорема. Код $ mathbb U $ с кодовым расстоянием $ d_ $
a) способен обнаружить от $ 1_ $ до $ d-1 $ (но не более) ошибок;
б) способен исправить от $ 1_ $ до $ leftlfloor displaystyle frac rightrfloor $ (но не более) ошибок. Здесь $ lfloor rfloor $ — целая часть числа.
Доказательство. Если $ U_1 $ — переданное кодовое слово, а $ V_ $ — полученный на выходе с канала вектор с $ tau_ $ ошибками, то $ rho(U_1,V)=tau $. Мы не сможем обнаружить ошибку если $ V_ $ совпадет с каким-то другим кодовым словом $ U_2 $, т.е. при условии $ rho(U_2,V)=0 $. Оценим $ rho(U_2,V) $ при условии, что $ tau le d-1 $. По неравенству треугольника 3 получаем $$ rho(U_2,V) ge rho(U_1,U_2)-rho(U_1,V) ge d-tau ge 1>0 . $$ Для доказательства части б) предположим, что $ 2,tau le d-1 $. Тогда те же рассуждения приведут к заключению $$ rho(U_2,V) ge d-tau ge (2,tau+1)-t > tau = rho(U_1,V) , $$ т.е. вектор $ V_ $ ближе к $ U_1 $, чем к любому другому кодовому слову. ♦
Пример. Код Адамара строится на основании матрицы Адамара — квадратной матрицы, элементами которой являются только числа $ $; при этом ее строки (как, впрочем, и столбцы) попарно ортогональны. Так, матрица Адамара порядка $ 8_ $ —
$$ H=left( begin 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 \ -1 & 1 &-1 & 1 & -1 & 1 &-1 & 1\ 1 & 1 & -1 & -1 & 1 & 1 & -1 & -1 \ -1 & 1 & 1 & -1 & -1 & 1 & 1 & -1 \ 1 & 1 & 1 & 1 & -1 & -1 & -1 & -1 \ -1 & 1 &-1 & 1 & 1 & -1 &1 & -1\ 1 & 1 & -1 & -1 & -1 & -1 & 1 & 1 \ -1 & 1 & 1 & -1 & 1 & -1 & -1 & 1 end right) . $$ Код строится следующим образом. Берутся строки матрицы $ H_ $ и умножаются на $ +1 $ и на $ -1 $; в каждой строке множества $$ H^,H^,dots,H^,-H^,-H^,dots,-H^ $$ производится замена $ +1 to 0, -1 to 1 $. Получаются $ 16 $ векторов $$ (00000000), (10101010), (00110011), (10011001), (00001111), (10100101), (00111100), (10010110), $$ $$ (11111111), (01010101), (11001100), (01100110), (11110000), (01011010), (11000011), (01101001), $$ которые обозначим $ U_1,dots,U_8,U_,dots,U_ $. Поскольку строки $ pm H^ $ и $ pm H^ $ ортогональны при $ jne k_ $ и состоят только из чисел $ pm 1 $, то ровно в половине своих элементов они должны совпадать, а в половине — быть противоположными. Соответствующие им векторы $ U_ $ будут совпадать в половине своих компонент и различаться в оставшихся. Таким образом $$ rho( U_, U_) = 4 quad npu quad jne k, rho( U_, U_) = 8 , $$ и кодовое расстояние равно $ 4_ $. В соответствии с теоремой, этот код способен обнаружить до трех ошибок, но исправить только одну. Так, к примеру, если при передаче по каналу связи слова $ U_8=(00111100) $ возникает только одна ошибка и на выходе получаем $ V_8= (00111101) $, то $ rho(U_8,V_8)=1 $, в то время как $ rho(U_j,V_8)ge 3 $ для других кодовых слов. Если же количество ошибок возрастет до двух — $ tilde V_8= (00111111) $, — то $ rho(U_8,tilde V_8)=2 $, но при этом также $ rho(U_9,tilde V_8)=2 $. Ошибка обнаружена, но однозначное декодирование невозможно. ♦
Теорема. Если существует матрица Адамара порядка $ n_>2 $, то
а) $ n_ $ кратно $ 4_ $, и
б) существует код $ mathbb U subset mathbb V^n $, состоящий из $ 2,n $ кодовых слов, для которого кодовое расстояние $ d=n/2 $.
Проблема построения кодов Адамара заключается в том, что существование матриц Адамара произвольного порядка $ n_ $ кратного $ 4_ $ составляет содержание не доказанной 2) гипотезы Адамара. Хотя для многих частных случаев $ n_ $ (например, для $ n=2^m, m in mathbb N $, см. ☞ ЗДЕСЬ ) матрицы Адамара построены.
Теорема. Если код $ mathbb U subset mathbb V^n $ может исправлять самое большее $ m_ $ ошибок, то количество $ s_ $ его слов должно удовлетворять следующему неравенству
Число в правой части неравенства называется верхней границей Хэмминга для числа кодовых слов.
Доказательство. Для простоты предположим, что одно из кодовых слов кода $ mathbb U $ совпадает с нулевым вектором: $ U_1=mathbb O_ $. Все векторы пространства $ mathbb V_n $, отстоящие от $ U_1 $ на расстояние $ 1_ $ заключаются во множестве $$ (100dots 0), (010 dots 0), dots, (000 dots 1) ; $$ их как раз $ n=C_n^1 $ штук. Векторы из $ mathbb V^n $, отстоящие от $ mathbb O_ $ на расстояние $ 2_ $ получаются в ходе расстановки двух цифр $ 1_ $ в произвольных местах нулевого вектора. Нахождение количества способов такой расстановки относится к задачам комбинаторики, и решение этой задачи можно найти ☞ ЗДЕСЬ. Оно равно как раз $ C_n^=n(n-1)/2 $. Аналогичная задача расстановки $ j_ $ единиц в $ n_ $-векторе имеет решением число $ C_n^j $. Таким образом общее количество векторов, отстоящих от $ mathbb O_ $ на расстояние $ le m_ $ равно $ C_n^1+dots+C_n^m $. Вместе в самим $ mathbb O_ $-вектором получаем как раз число из знаменателя границы Хэмминга.
Предыдущие рассуждения будут справедливы и для любого другого кодового слова из $ mathbb U $ — каждое из них можно «окружить $ m_ $-окрестностью» и каждая из этих окрестностей будет содержать $$ 1+C_n^1+dots+C_n^m $$ векторов из $ mathbb V^n $. По предположению теоремы, эти окрестности не должны пересекаться. Но тогда общее количество векторов $ mathbb V^n $, попавших в эти окрестности (для всех $ s_ $ кодовых слов) не должно превышать количества векторов в $ mathbb V^n $, т.е. $ 2^ $. ♦
Доказать, что если $ n_ $ — нечетно, а $ m=lfloor n/2 rfloor=(n-1)/2 $ то верхняя граница Хэмминга равна в точности $ 2_ $.
Пример. Для $ n=10 $ имеем
| $ m_ $ | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| $ sle $ | 93 | 18 | 5 | 2 | 1 |
Коды, для которых верхняя граница Хэмминга достигается, называются совершенными.
Видео:2 Расстояния Хэмминга и ЛевенштейнаСкачать

Линейные коды
Идея, лежащая в основе этих кодов достаточно проста: это — обобщение понятия контрольной суммы. Если вектор $ (x_1,dots,x_k) in mathbb V^k $ содержит информационные биты, которые требуется передать, то для контроля целостности при передаче их по каналу присоединим к этому вектору еще один «служебный» бит с вычисленным значением $$ x_=x_1+dots+x_k pmod . $$ Очевидно, $ x_=1 $ если среди информационных битов содержится нечетное число единиц, и $ x_=0 $ в противном случае. Поэтому этот бит называют битом четности. Кодовым словом становится вектор $$ X=(x_1,dots,x_k,x_) in mathbb V^ . $$ По прохождении его по каналу, для полученного вектора $ Y=(y_1,dots,y_k,y_) $ производится проверка условия $$ y_ = y_1+dots+y_k pmod . $$ Если оно не выполнено, то при передаче произошла ошибка. Если же сравнение оказывается справедливым, то это еще не значит, что ошибки при передаче нет — поскольку комбинация из двух (или любого четного числа) ошибок не изменит бита четности.
Для более вероятного обнаружения ошибки вычислим несколько контрольных сумм — выбирая различные разряды информационного вектора $ (x_1,dots,x_k) $: $$ begin x_&=&x_+&dots&+x_ pmod, \ x_&=&x_+&dots&+x_ pmod, \ vdots & & vdots \ x_n &=&x_+& dots & +x_ pmod. end $$ Полученные биты присоединим к информационному блоку. Кодовым словом будет вектор $$ X=(x_1,dots,x_k,x_,dots,x_n) in mathbb V^n , $$ который и поступает в канал связи. По прохождении его по каналу, для соответствующих разрядов полученного вектора $ Y_ $ проверяется выполнимость контрольных сравнений. Если все они выполняются, то ошибка передачи считается невыявленной.
На первый взгляд кажется, что при увеличении количества контрольных сумм увеличивается и вероятность обнаружения ошибки передачи. Однако с увеличением количества разрядов кодового слова увеличивается и вероятность появления этой ошибки.
Пример. Если вероятность ошибочной передачи одного бита по каналу равна $ P_1=0.1 $, то вероятность появления хотя бы одной ошибки при передаче $ k_ $ битов равна $ P_k= 1-(0.9)^k $, т.е.
| $ k $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| $ P_k $ | 0.1 | 0.19 | 0.271 | 0.344 | 0.410 | 0.469 | 0.522 | 0.570 | 0.613 | 0.651 |
Обычно, количество проверочных соотношений берется меньшим (и даже много меньшим) количества информационных битов 3) . Осталось только понять как составлять эти проверочные соотношения так, чтобы они смогли реагировать на ошибки передачи по каналу связи.
Сначала формализуем предложенную выше идею. В пространстве $ mathbb V^n $ выделим некоторое подпространство $ mathbb V^n_ $, состоящее из векторов $$ (x_1,dots,x_k,x_,dots,x_n) , $$ первые $ k_ $ компонентов которых считаются произвольными, а оставшиеся $ n-k_ $ полностью определяются первыми посредством заданных линейных соотношений: $$ begin x_&=&h_x_1+&dots&+h_x_k pmod \ vdots & & vdots \ x_n &=&h_x_1+& dots & +h_x_k pmod end qquad npu qquad <h_> subset . $$ Кодовые слова выбираются именно из подпространства $ mathbb V^n_ $, их количество равно $ operatorname (mathbb V^n_ )=2^k $. При этом начальная часть каждого кодового слова, т.е. вектор $ (x_1,dots,x_k) $, заключает информацию, которую нужно передать — эти разряды называются информационными. Остальные разряды кодового слова, т.е. биты вектора $ (x_,dots,x_n) $, которые вычисляются с помощью выписанных линейных соотношений, являются служебными — они называются проверочными и предназначены для контроля целостности передачи информационных разрядов по каналу связи (и/или коррекции ошибок). Код такого типа называется линейным (n,k)-кодом.
Пример. Пусть $ n=5, k=3 $. Пусть проверочные биты связаны с информационными соотношениями
$$ x_4=x_1 + x_2, x_5=x_1 + x_3 . $$ Тогда $ mathbb V^5_ $ состоит из векторов $$ (00000), (10011), (01010), (00101), (11001), (10110), (01111), (11100) . $$ ♦
Для описания пространства $ mathbb V^n_ $ привлечем аппарат теории матриц. С одной стороны, в этом подпространстве можно выбрать базис — систему из $ k_ $ линейно независимых векторов: обозначим их $ $. Матрица, составленная из этих векторов-строк, $$ mathbf G=left( begin X_1 \ vdots \ X_k end right)_ $$ называется порождающей матрицей кода. Так, в только что приведенном примере в качестве порождающей матрицы может быть выбрана $$ mathbf G= left( begin 1 & 0 & 0 & 1 & 1 \ 0 & 1 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 &1 end right) qquad mbox qquad mathbf G= left( begin 1 & 0 & 0 & 1 & 1 \ 1 & 1 & 0 & 0 & 1 \ 1 & 1 & 1 & 0 & 0 end right) . $$ Любая строка $ X_ $ кода может быть получена как линейная комбинация строк порождающей матрицы: $$ X=alpha_1 X_1+alpha_2X_2+dots+alpha_k X_k quad npu quad subset . $$ Можно переписать это равенство с использованием операции матричного умножения: $$ X=(alpha_1,dots,alpha_k) mathbf G . $$ Так, продолжая рассмотрение предыдущего примера: $$ (x_1,x_2,x_3,x_4,x_5)=(x_1,x_2,x_3) left( begin 1 & 0 & 0 & 1 & 1 \ 0 & 1 & 0 & 1 & 0 \ 0 & 0 & 1 & 0 &1 end right)= $$ $$ =(x_1+x_2,x_2+x_3,x_3) left( begin 1 & 0 & 0 & 1 & 1 \ 1 & 1 & 0 & 0 & 1 \ 1 & 1 & 1 & 0 & 0 end right) pmod . $$ С другой стороны, для описания $ mathbb V^n_ $ имеются проверочные соотношения. Объединяя их в систему линейных уравнений, перепишем их с использованием матричного формализма: $$ (x_1,dots,x_k,x_,dots,x_n) cdot left(begin h_ & h_ & dots &h_ \ h_ & h_ & dots & h_ \ vdots & & & vdots \ h_ & h_ & dots & h_ \ -1 & 0 & dots & 0 \ 0 & -1 & dots & 0 \ vdots & & ddots & vdots \ 0 & 0 & dots & -1 end right)= (0,0,dots,0)_ $$ или, в альтернативном виде, с использованием транспонирования 4) : $$ underbrace<left(begin h_ & h_ & dots &h_ & 1 & 0 & dots & 0 \ h_ & h_ & dots & h_& 0 & 1 & dots & 0 \ vdots & & & vdots & dots & & ddots & vdots \ h_ & h_ & dots & h_ & 0 & 0 & dots & 1 \ end right)>_left( begin x_1 \ x_2 \ vdots \ x_n end right) =left( begin 0 \ 0 \ vdots \ 0 end right)_ $$ Матрица $ mathbf H_ $ порядка $ (n-k)times n $ называется проверочной матрицей кода 5) . Хотя вторая форма записи (когда вектор-столбец неизвестных стоит справа от матрицы) более привычна для линейной алгебры, в теории кодирования чаще используется именно первая — с вектором-строкой $ X_ $ слева от матрицы: $$ Xcdot mathbf H^ = mathbb O_ . $$ Для приведенного выше примера проверочные соотношения переписываются в виде $$ x_1 + x_2 +x_4=0, x_1 + x_3 + x_5=0 $$ и, следовательно, проверочная матрица: $$ mathbf H= left( begin 1 & 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 0 & 1 end right) . $$
Теорема 1. Имеет место матричное равенство
$$ mathbf G cdot mathbf H^ = mathbb O_ .$$
Доказательство. Каждая строка матрицы $ mathbf G $ — это кодовое слово $ X_ $ , которое, по предположению, должно удовлетворять проверочным соотношениям $ X_j cdot mathbf H^ = mathbb O_ $. Равенство из теоремы — это объединение всех таких соотношений в матричной форме. Фактически, порождающая матрица $ mathbf G $ состоит из строк, составляющих фундаментальную систему решений системы уравнений $ X mathbf H^= mathbb O $. ♦
Если проверочная матрица имеет вид $ mathbf H=left[ P^ mid E_ right] $, где $ E_ $ — единичная матрица порядка $ n — k_ $, $ P_ $ — некоторая матрица порядка $ k times (n-k) $, а $ mid_ $ означает операцию конкатенации, то порождающая матрица может быть выбрана в виде $ mathbf G = left[ E_k mid P right] $.
Доказательство следует из предыдущей теоремы, правила умножения блочных матриц — $$ mathbf G cdot mathbf H^ = E_k cdot P + P cdot E_ = 2P equiv mathbb O_ pmod , $$ и того факта, что строки матрицы $ mathbf G $ линейно независимы. Последнее обстоятельство обеспечивается структурой этой матрицы: первые $ k_ $ ее столбцов являются столбцами единичной матрицы. Любая комбинация $$ alpha_1 mathbf G^+dots+alpha_k mathbf G^ $$ строк матрицы дает строку $ (alpha_1,dots,alpha_k,dots ) $ и для обращения ее в нулевую необходимо, чтобы $ alpha_1=0,dots,alpha_k=0 $. ♦
Теорема 2. Кодовое расстояние линейного подпространства $ mathbb V^_ $ равно минимальному весу его ненулевых кодовых слов:
Доказательство. Линейное подпространство замкнуто относительно операции сложения (вычитания) векторов. Поэтому если $ subset mathbb V^_ $, то и $ U_1-U_2 in mathbb V^_ $, а также $ mathbb O in V^_ $. Тогда $$ rho(U_1,U_2)=rho(U_1-U_2, mathbb O)= w(U_1-U_2) . $$ ♦
Кодовое расстояние дает третью характеристику линейного кода — теперь он описывается набором чисел $ (n,k,d) $.
Теорема 3. Пусть $ d_ $ означает кодовое расстояние кода $ mathbb V^_ $ с проверочной матрицей $ mathbf H $. Тогда любое подмножество из $ ell_ $ столбцов этой матрицы будет линейно независимо при $ ell ell $.
Доказательство. Если $ d_ $ — кодовое расстояние, то, в соответствии с теоремой 2, ни одно ненулевое кодовое слово $ Xin mathbb V^_ $ не должно иметь вес, меньший $ d_ $. Если предположить, что столбцы $ <mathbf H_,dots,mathbf H_<[i_]>> $ линейно зависимы при $ ell ♦
Видео:Алгоритмы и структуры данных JavaScript. Вычисление расстояния Хэмминга. Урок #5Скачать

Испровление ашибок
До сих пор мы не накладывали ни каких дополнительных ограничений ни на порождающую ни на проверочную матрицы кода: любая из них могла быть выбрана почти произвольной.
Теперь обратимся собственно к задаче обнаружения (а также возможной коррекции) ошибок при передаче кодового слова по зашумленному каналу связи.
Если $ Xin mathbb V^_ $ — кодовое слово, а $ Yin mathbb V^n $ — вектор, получившийся по прохождении этого слова по каналу, то $ Y-X $ называется вектором ошибок. Понятно, что при $ w(Y-X)=0 $ ошибки при передаче нет.
Предположим, что $ w(Y-X)=1 $, т.е. что при передаче произошла ошибка ровно в одном разряде кодового слова $ X_ $. Попробуем ее обнаружить исходя из предположения, что кодовое слово выбиралось во множестве $ mathbb V^_ $ линейного $ (n,k) $-кода, определенного в предыдущем пункте при какой-то проверочной матрице $ mathbf H $. Если для полученного вектора $ Y_ $ выполняются все проверочные условия: $$ Y cdot mathbf H^ = mathbb O_ , $$ (или, что то же $ Y in mathbb V^_ $), то ошибка передачи считается не выявленной.
Для произвольного вектора $ Y in mathbb V^ $ вектор-строка $$ S=Y cdot mathbf H^ in mathbb V^ $$ называется синдромом вектора Y. C точки зрения линейной алгебры его можно интерпретировать как показатель отхода вектора $ Y_ $ от гиперплоскости, заданной системой однородных уравнений $ Xcdot mathbf H^=mathbb O $.
Если синдром $ S_ $ ненулевой: $ Y cdot mathbf H^ ne mathbb O_ $, то полученный вектор $ Y_ $ не принадлежит множеству $ mathbb V^_ $ допустимых кодовых слов. Факт ошибки подтвержден. Изначально мы предположили, что произошла только одна ошибка, т.е. $$ Y-X= _j = big(underbrace_,0,dots,0big) $$ при некотором $ jin $. Тогда $$ S= Y cdot mathbf H^ = (X+_j) cdot mathbf H^=Xcdot mathbf H^+ _j cdot mathbf H^= $$ $$ =mathbb O_ + mathbf H_^ = mathbf H_^ $$ при $ mathbf H_ $ означающем $ j_ $-й столбец проверочной матрицы $ mathbf H $. Таким образом получили соответствие $$ _ mathbf mbox mathbf mbox $$ И, следовательно, мы получили возможность обнаружить место повреждения — по факту совпадения синдрома со столбцом проверочной матрицы. К сожалению, реальность оказывается более сложной…
Пример. В примере предыдущего пункта проверочная матрица была выбрана в виде
$$ mathbf H= left( begin 1 & 1 & 0 & 1 & 0 \ 1 & 0 & 1 & 0 & 1 end right) . $$ Если при передаче кодового слова $ (10011) $ произошла ошибка в первом бите, т.е. $ Y=(00011) $, то синдром $$ S=Y cdot mathbf H^ = (11) $$ однозначно укажет на номер столбца матрицы $ mathbf H $. Если же ошибка произошла в четвертом бите, т.е. $ Y=(10001) $, то $$ S=(10) , $$ но таких 6) столбцов в матрице $ mathbf H $ два! ♦
Вывод. Для однозначного обнаружения места ошибки 7) достаточно, чтобы все столбцы матрицы $ mathbf H $ были различными.
Столбцами этой матрицы являются транспонированные строки пространства $ mathbb V^ $.
Видео:Алгоритм Хемминга (Код Хэмминга)Скачать

Построение кода
Итак, исходя из соображений, завершающих предыдущий пункт, будем строить код, исправляющий одну ошибку, беря за стартовую точку именно матрицу $ mathbf H $. Выбираем ее произвольного порядка $ Mtimes N $ при $ in mathbb N, M ☞ ПУНКТА — строим порождающую матрицу: $$ mathbf G_ = left[ E_ mid tilde P^ right] . $$ Строки матрицы $ mathbf G $ могут быть взяты в качестве базисных векторов подпространства кодовых слов.
Пример. Пусть $ M=2 $. Здесь имеем единственный вариант:
$$ mathbf H_ = left( begin 1 & 1 & 0 \ 1 & 0 & 1 end right) , $$ поскольку в $ mathbb V^2 $ имеется лишь одна ненулевая строка, отличная от $ (10) $ и $ (01) $. Таким образом $ N=3 $ и $$ mathbf G_=( 1, 1, 1 ) . $$ Следовательно, подпространство кодовых слов в $ mathbb V^3 $ является одномерным, и имеем всего два возможных кодовых слова: $ (000) $ и $ (111) $.
Пусть $ M=3 $. В $ mathbb V^3 $ имеется уже большой выбор строк, отличных от $ (100), (010), (001) $. Так, можно взять $$ mathbf H_ = left( begin 1 & 1 & 0 & 0 \ 1 & 0 & 1 & 0 \ 1 & 0 & 0 & 1 end right) quad mbox quad mathbf H_ = left( begin 1 & 0 & 1 & 0 & 0 \ 1 & 1 & 0 & 1 & 0 \ 0 & 1 & 0 & 0 & 1 end right) $$ $$ mbox quad mathbf H_ = left( begin 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 0 & 0 & 1 & 0 \ 0 & 1 & 1 & 0 & 0 & 1 end right) quad mbox quad mathbf H_ = left( begin 1 & 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 0 & 1 end right) . $$ Соответственно, $$ mathbf G= (1, 1, 1, 1) quad quad mbox quad mathbf G= left( begin 1 & 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 1 & 1 end right) quad $$ $$ mbox quad mathbf G= left( begin 1 & 0 & 0 & 1 & 1 & 0 \ 0 & 1 & 0 & 0 & 1 & 1 \ 0 & 0 & 1 & 1 & 0 & 1 end right) quad quad mbox quad mathbf G= left( begin 1 & 0 & 0 & 0 & 1 & 1 & 1 \ 0 & 1 & 0 & 0 & 1 & 1 & 0 \ 0 & 0 & 1 & 0 & 0 & 1 & 1 \ 0 & 0 & 0 & 1 & 1 & 0 & 1 end right) . $$ Кодовых векторов в соответствующих кодах будет $ 2^1,2^2,2^3,2^4 $. Любой из них способен исправить одну ошибку, полученную в ходе передачи. ♦
Если поставить задачу максимизации числа кодовых слов, то матрицу $ mathbf H $ следует выбирать самой широкой, т.е. делать $ N_ $ максимально возможным. При фиксированном $ M_ $ это достигается при выборе $ N=2^M-1 $. Тогда соответствующий линейный $ (n,k) $-код имеет значения параметров $ n=2^M-1,k=2^M-M-1 $, и именно он обычно и выбирается в качестве кода Хэмминга.
Найдем величину его кодового расстояния $ d_ $. В соответствии с теоремой $ 3 $ из ☞ ПУНКТА, $ d>ell $, если любое подмножество из $ ell_ $ столбцов матрицы $ mathbf H $ линейно независимо. Поскольку столбцы проверочной матрицы кода Хэмминга все различны, то любая пара из них линейно независима (свойство 3 ☞ ЗДЕСЬ ). Следовательно, $ d>2 $. По теореме из ☞ ПУНКТА, получаем —
Пример. Для проверочной матрицы $ (7,4) $-кода Хэмминга
$$ mathbf H_ = left( begin 1 & 1 & 0 & 1 & 1 & 0 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 & 0 \ 1 & 0 & 1 & 1 & 0 & 0 & 1 end right) $$ вектор $ X=(0011110) $ является кодовым. Если при передаче произошла лишь одна ошибка и на выходе канала получили вектор $ Y=(1011110) $, то синдром этого вектора $ S=Y mathbf H^=(111) $. Поскольку $ S^ $ совпадает с первым столбцом матрицы $ mathbf H $, то заключаем, что ошибка произошла в первом разряде. Тут же исправляем его на противоположный: $ X=Y+mathfrak e_1 $.
Если при передаче произошло две ошибки и на выходе канала получили вектор $ tilde Y=(1011010) $, то синдром этого вектора $ S=tilde Y mathbf H^=(011) $. Поскольку синдром ненулевой, то факт наличия ошибки подтвержден. Однако корректно исправить ее — по аналогии с предыдущим — не удается. $ S^ $ совпадает с третьим столбцом матрицы $ mathbf H $, но в третьем разряде полученного вектора ошибки нет.
Наконец, если при передаче произошли три ошибки и на выходе канала получили вектор $ widehat Y=(1011011) $, то синдром этого вектора $ S=widehat Y mathbf H^=(010) $. Наличие ошибки подтверждено, исправление невозможно. Если же — при передаче того же вектора $ X=(0011110) $ — получаем вектор $ widehat Y_1=(1111111) $ (также с тремя ошибками), то его синдром оказывается нулевым: $ widehat Y_1 mathbf H^=(000) $ и ошибка не обнаруживается. ♦
Проблема сравнения синдрома полученного вектора $ Y_ $ со столбцами проверочной матрицы $ mathbf H $ с целью определения места ошибки — не такая тривиальная, особенно для больших $ n_ $. Для упрощения этой процедуры воспользуемся следующим простым соображением. Размещение проверочных разрядов в конце кодового слова обусловлено лишь соображениями удобства изложения учебного материала. С точки зрения практической реализации, $ n-k $ проверочных разрядов можно разместить в любых местах кодового слова $ X_ $ и даже «вразбивку», т.е. не подряд. Перестановке разрядов в кодовом слове будет соответствовать перестановка столбцов в матрице $ mathbf H $, при этом само множество столбцов остается неизменным — это транспонированные строки пространства $ mathbb V^ $ (ненулевые и различные). Рассмотрим $ (n,k) $-код Хэмминга при $ n=2^M-1,k=2^M-M-1, M ge 2 $. Тогда каждую ненулевую строку пространства $ mathbb V^= mathbb V^M $ можно интерпретировать как двоичное представление числа из множества $ $. Пусть $$ j=underline<_1_2 dots _ _>= _1 times 2^+_2 times 2^+dots+_ times 2+ _ quad npu quad < _j>_^Msubset quad — $$ — двоичное представление числа $ j_ $. Переупорядочим столбцы проверочной матрицы $ mathbf H $ так, чтобы $$ mathbf H_=left[ _1_2 dots _ _right]^ , $$ т.е. чтобы $ j_ $-й столбец содержал двоичное представление числа $ j_ $. При таком упорядочении, синдром произвольного вектора $ Y_ $, отличающегося от кодового слова $ X_ $ в единственном разряде, является двоичным представлением номера этого разряда: $$ <bf mbox> (Y)=mathbf (mbox) . $$
Осталось теперь выяснить какие разряды кодового слова содержат проверочные биты.
Пример. Для $ (7,4) $-кода Хэмминга матрицу $ mathbf H $, построенную в предыдущем примере, переупорядочим по столбцам; будем рассматривать ее в виде
$$ begin left( begin 0 & 0 & 0 & 1 & 1 & 1 & 1 \ 0 & 1 & 1 & 0 & 0 & 1 & 1 \ 1 & 0 & 1 & 0 & 1 & 0 & 1 end right) \ begin uparrow & uparrow & uparrow & uparrow & uparrow & uparrow & uparrow \ scriptstyle 1 & scriptstyle 2 & scriptstyle 3 & scriptstyle 4 & scriptstyle 5 & scriptstyle 6 & scriptstyle 7 end end $$ Распишем проверочные соотношения $ Xmathbf H^=mathbb O $ покомпонентно: $$ left< begin & & & x_4&+x_5&+x_6&+x_7=0 \ &x_2&+x_3& & & +x_6&+x_7=0 \ x_1& & +x_3& & +x_5 & & +x_7=0 end right. quad iff $$ $$ iff quad left< begin x_1& & +x_3& & +x_5 & & +x_7=0 \ &x_2&+x_3& & & +x_6&+x_7=0 \ & & & x_4&+x_5&+x_6&+x_7=0 end right. $$ Переписанные в последнем виде, эти уравнения представляют конечный пункт прямого хода метода Гаусса решения системы линейных уравнений, а именно — трапециевидную форму этой системы. Если бы мы поставили задачу поиска общего решения этой (однородной) системы и нахождения фундаментальной системы решений, то в качестве зависимых переменных однозначно бы выбрали $ x_1, x_2, x_4 $. Выпишем это общее решение 8) : $$ x_1=x_3+x_5+x_7, x_2=x_3+x_6+x_7, x_4=x_5+x_6+x_7 . $$ Это и есть проверочные соотношения, а проверочными разрядами кодового вектора являются $ 1_ $-й, $ 2_ $-й и $ 4_ $-й.
Проверим правильность этих рассуждений. Придадим оставшимся разрядам произвольные значения, например: $ x_3=1,x_5=1,x_6=0,x_7=1 $. Тогда $ x_1=1, x_2=0,x_4=0 $ и кодовый вектор $ X=(1010101) $. Пусть на выходе из канала он превратился в $ Y=(1000101) $. Синдром этого вектора $ Ymathbf H^=(011) $ — это двоичное представление числа $ 3_ $. И ведь действительно: ошибка — в третьем разряде! ♦
Алгоритм построения (n,k)-кода Хэмминга
для $ n=2^M-1,k=2^M-M-1, M ge 2 $.
1. Строится матрица $ mathbf H $ порядка $ M times (2^M-1) $ из столбцов, представляющих двоичные представления чисел $ $ (младшие разряды — внизу).
2. Проверочные разряды имеют номера, равные степеням двойки: $ 1,2,2^2,dots,2^ $.
3. Проверочные соотношения получаются из матричного представления $ Xmathbf H^=mathbb O $ выражением проверочных разрядов через информационные.
Является ли $ 8_ $-мибитный код Адамара из примера ☞ ПУНКТА линейным кодом?
Видео:Код Хэмминга. Самоконтролирующийся и самокорректирующийся код.Скачать

Источники
[1]. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. М.Мир. 1976.
[2]. Марков А.А. Введение в теорию кодирования. М.Наука. 1982
Видео:2020.10.13.Лекция 3.Метрика и вес Хэмминга Задача о подсчёте веса вектора (Сахалин)Скачать

Подсчет расстояния Хэмминга на большом наборе данных
Введение
Расстояние Хэмминга — это количество различающихся позиций для строк с одинаковой длинной. Например, HD( 100, 001 ) = 2.
Впервые проблема подсчета расстояния Хэмминга была поставлена Minsky и Papert в 1969 году [1], где задача сводилась к поиску всех строк из базы данных, которые находятся в пределах заданного расстояния Хэмминга к запрашиваемой.
Подобная задача является необычайно простой, но поиск ее эффективного решения до сих пор остается на повестке дня.
Расстояние Хэмминга уже довольно широко используется для различных задач, таких как поиск близких дубликатов, распознавание образов, классификация документов, исправление ошибок, обнаружения вирусов и т.д.
Например, Manku и сотоварищи предложили решение проблемы кластеризации дубликатов при индексации веб документов на основе подсчета расстояния Хэмминга [2].
Также Miller и друзья предложили концепцию поиска песен по заданному аудио фрагменту [3], [4].
Подобные решения были использованы и для задачи поиска изображений и распознавание сетчатки [5], [6] и т.д.
Описание проблемы
Имеется база данных бинарных строк T, размером n, где длина каждой строки m. Запрашиваемая строка a и требуемое расстояние Хэмминга k.
Задача сводится к поиску всех строк, которые находятся в пределах расстояния k.
В оригинальной концепции алгоритма рассматривается два варианта задачи: статическая и динамическая.
— В статической задачи расстояние k предопределено заранее.
— В динамической, наоборот, требуемое расстояние заранее неизвестно.
В статье описывается решение только статической задачи.
Описание алгоритма HEngine для статической задачи
Данная реализация фокусируется на поиске строк в пределах k = ⌊k/2⌋ + 1
обязательно найдется, по крайней мере, q= r − ⌊k/2⌋ подстрок, когда их расстояние не будет превышать единицу, HD( ai, bi ) = ⌊k/2⌋ + 1
Длина первых r − (m mod r) подстрок будет иметь длину ⌊m / r⌋, а последние m mod r подстроки ⌈m/r⌉. Где m — это длина строки, ⌊ — округление до ближайшего снизу, а ⌉ округление до ближайшего сверху.
Теперь тоже самое, только на примере:
Даны две бинарные строки длиной m = 8 бит: A = 11110000 и B = 11010001, расстояние между ними k = 2.
Выбираем фактор сегментации r = 2 / 2 + 1 = 2, т. е. всего будет 2 подстроки длиной m/r = 4 бита.
a1 = 1111, a2 = 0000
b1 = 1101, b2 = 0001
Если мы сейчас подсчитаем расстояние между соответствующими подстроками, то, по крайней мере, (q = 2 — 2/2 = 1) одна подстрока совпадет или их расстояние не будет превышать единицу.
Что и видим:
HD( a1, b1 ) = HD( 1111, 1101 ) = 1
и
HD( a2, b2 ) = HD( 0000, 0001 ) = 1
Подстроки базовой строки были названы сигнатурами.
Сигнатуры или подстроки a1 и b1 (a2 и b2, a3 и b3 …, ar и br) называются совместимыми с друг другом, а если их количество отличающихся битов не больше единицы, то эти сигнатуры называются совпадающими.
И главная идея алгоритма HEngine — это подготовить базу данных таким образом, чтобы найти совпадающие сигнатуры и затем выбрать те строки, которые находятся в пределах требуемого расстояния Хэмминга.
Предварительная обработка базы данных
Нам уже известно, что если правильно поделить строку на подстроки, то, по крайней мере, одна подстрока совпадет с соответствующей подстрокой либо количество отличающихся битов не будет превышать единицу (сигнатуры совпадут).
Это означает, что нам не надо проводить полный перебор по всем строкам из базы данных, а требуется сначала найти те сигнатуры, которые совпадут, т.е. подстроки будут отличаться максимум на единицу.
Но как производить поиск по подстрокам?
Метод двоичного поиска должен неплохо с этим справляться. Но он требует, чтобы список строк был отсортирован. Но у нас получается несколько подстрок из одной строки. Что бы произвести двоичный поиск по списку подстрок, надо чтобы каждый такой список был отсортирован заранее.
Поэтому здесь напрашивается метод расширения базы данных, т. е. созданию нескольких таблиц, каждая для своей подстроки или сигнатуры. (Такая таблица называется таблицей сигнатур. А совокупность таких таблиц — набор сигнатур).
В оригинальной версии алгоритма еще описывается перестановка подстрок таким образом, чтобы выбранные подстроки были на первом месте. Это делается больше для удобства реализации и для дальнейших оптимизаций алгоритма:
Имеется строка A, которая делится на 3 подстроки, a1, a2, a3, полный список перестановок будет соответственно:
a1, a2, a3
a2, a1, a3
a3, a1, a2
Затем эти таблицы сигнатур сортируются.
Реализация поиска
На этом этапе, после предварительной обработки базы данных мы имеем несколько копий отсортированных таблиц, каждая для своей подстроки.
Очевидно, что если мы хотим сперва найти подстроки, необходимо из запрашиваемой строки получить сигнатуры тем же способом, который был использован при создании таблиц сигнатур.
Так же нам известно, что необходимые подстроки отличаются максимум на один элемент. И чтобы найти их потребуется воспользоваться методом расширения запроса (query expansion).
Другими словами требуется для выбранной подстроки сгенерировать все комбинации включая саму эту подстроку, при которых различие будет максимум на один элемент. Количество таких комбинаций будет равна длине подстроки + 1.
А дальше производить двоичный поиск в соответствующей таблице сигнатур на полное совпадение.
Такие действия надо произвести для всех подстрок и для всех таблиц.
И в самом конце потребуется отфильтровать те строки, которые не вмещаются в заданный предел расстояния Хэмминга. Т.е. произвести линейный поиск по найденным строкам и оставить только те строки, которые отвечают условию HD( a, b ) 11111111
1000 0001 => 10000001
0011 1110 => 00111110
4. Сортируем таблицы. Каждую в отдельности.
Т1
0011 => 00111110
1000 => 10000001
1111 => 11111111
Т2
0001 => 10000001
1110 => 00111110
1111=> 11111111
На этом предварительная обработка закончена. И приступаем к поиску.
1. Получаем сигнатуры запрашиваемой строки.
Искомая строка 10111110 разбивается на сигнатуры. Получается 1011 и 1100, соответственно первая для первой таблицы, а вторая для второй.
2. Генерируем все комбинации отличающихся на единицу.
Количество вариантов будет 5.
2.1 Для первой подстроки 1011:
1011
0011
1111
1001
1010
2.2 Для второй подстроки 1100:
1100
0100
1000
1110
1101
3. Двоичный поиск.
3.1 Для всех сгенерированных вариантов первой подстроки 1011 производим двоичный поиск в первой таблице на полное совпадение.
1011
0011 == 0011 => 00111110
1111 == 1111 => 11111111
1001
1010
Найдено две подстроки.
3.2 Теперь для всех вариантов второй подстроки 1100 производим двоичный поиск во второй таблице.
1100
0100
1000
1110 == 1110 => 00111110
1101
Найдена одна подстрока.
4. Объедением результаты в один список:
00111110
11111111
5. Линейно проверяем на соответствие и отфильтровываем неподходящие по условию
Видео:Кодирование кодом ХэммингаСкачать

Расстояние Хемминга
Американский математик Хемминг исследовал, от чего зависит данный код, будет ли он обнаруживать ошибки и когда может их исправлять. Интуитивно ясно, что это зависит от того, как разнесены между собой кодовые слова и сколько ошибок может появиться в передаваемом слове. M ы сейчас формализуем следующую идею. При кодировании надо согласовывать число возможных ошибок в передаваемом слове так, чтобы при изменении передаваемого кодового слова оно оставалось более близким к исходному кодовому слову, чем к любому другому кодовому слову.
Определение 13.1.Рассмотрим на множестве всех двоичных слов в алфавите В = длины т расстояние d ( x , у ), которое равно числу несовпадающих позиций этих слов. Например, Для слов х = 011101, у = 101010 расстояние равно d ( x , y ) = 5. Это расстояние носит название расстояние Хемминга .
Можно показать, что расстояние Хемминга удовлетворяет аксиомам метрического пространства:
1) d ( x , у ) ≥ 0, d ( x , у ) = 0 тогда и только тогда, когда х = у;
Теорема 13.1(об обнаруживающем коде ). Код является обнаруживающим в случае, когда в передаваемом слове имеется не более чем k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами
Теорема 13.2(об исправляющем коде .). Код является исправляющим все ошибки в случае, когда в передаваемом слове имеется не более k ошибок, тогда и только тогда, когда наименьшее расстояние между кодовыми словами
Доказательство . Доказательства этих теорем аналогичны. Поэтому докажем только последнюю теорему.
Достаточность . Пусть для любых кодовых слов имеем d ( b 1, b 2) ≥ 2k + 1. Если при передаче кодового слова b 1произошло не более k ошибок, то для принятого слова с имеем d ( b 1, c ) ≤ k . Но из неравенства треугольника для любого другого кодового слова b 2имеем d ( b 1, с ) + d ( c , b 2) ≥ d ( b 1, b 2) ≥ 2 k + 1. Следовательно, от принятого слова до любого другого кодового слова расстояние d ( c , b 2) ≥ k + 1, т. е. больше, чем до b 1. Поэтому по принятому слову с можно однозначно найти ближайшее кодовое слово b 1и далее декодировать его.
Необходимость . От противного. Предположим, что минимальное расстояние между кодовыми словами меньше, чем 2 k + 1. Тогда найдутся два кодовых слова, расстояние между которыми будет d ( b 1, b 2) ≤ 2 k . Пусть при передаче слова b 1принятое слово с находится на отрезке между словами b 1, b 2и имеет ровно k ошибок. Тогда d ( c , b 1) = k , d ( c , b 2) = d ( b 1, b 2) – d ( c , b 1) ≤ k . Тем самым по слову с нельзя однозначно восстановить кодовое слово, которое было передано, b 1или b 2. Пришли к противоречию.
Пример 13.3. Рассмотрим следующие пятиразрядные коды слов длиной 2 в алфавите В = :
Минимальное расстояние между различными кодовыми словами равно d ( bi, bj) = 3. В силу первой теоремы об обнаруживающем коде, этот код способен обнаруживать не более двух ошибок в слове. В силу второй теоремы, код способен исправлять не более одной ошибки в слове.
Групповые коды
Рассмотрим подробнее коды слов в алфавите В = . Если для слов длиной т используются кодовые слова длиной n , то такие коды будем называть (т , п )-коды. Всего слов длиной m равно 2 m. Чтобы задать (т , п )-код, можно перечислить кодовые слова для всех возможных слов длиной m , как в предыдущем примере. Более экономным способом задания кодовых слов является матричное задание.
В этом случае задается порождающая матрица G = ∣∣ gij∣∣ порядка т × п из 0 и 1. Кодовые слова определяются каждый раз по слову а = а 1a 2. атпутем умножения этого слова слева, как вектора, на порождающую матрицу
Здесь сложение определяется по модулю 2. Для того чтобы разным словам соответствовали разные кодовые слова, достаточно иметь в матрице G единичный базисный минор порядка т , например крайний левый.
Пример 13.4. Рассмотрим порождающую матрицу
Эта матрица задает (3, 4)-код. При этом три первые символа в кодовом слове информационные, а четвертый — контрольный. Он равен 0, если четное число единиц в исходном слове, и 1, если нечетное число единиц. Например, для слова а = 101 кодом будет b = aG = 1010. Минимальное расстояние Хемминга между кодовыми словами равно d ( bi, bj) = 2. Поэтому это — код, обнаруживающий однократную ошибку.
Определение 13.2.Код называется групповым, если множество всех кодовых слов образует группу. Число единиц в слове а называется весамслова и обозначается 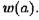
Теорема 13.3.Пусть имеется групповой (т , п )-код. Тогда коммутативная группа К всех кодовых слов является подгруппой коммутативной группы С всех слов длины п , которые могут быть приняты в канале связи. Наименьшее расстояние между кодовыми словами равно наименьшему весу ненулевого кодового слова и
Рассмотрим фактор-группу С / K . Смежные классы здесь будут определяться сдвигом е + b , b ∈ K .
В качестве представителя смежного класса выберем элемент с наименьшим весом. Будем такие элементы называть лидерами смежного класса .
Если лидеры трактовать как векторы ошибок, то каждый смежный класс — множество искаженных слов в канале связи с фиксированным вектором ошибок, в частности при е = 0 имеем смежный класс слов без искажений, т. е. множество всех кодовых слов. Процесс коррекции и декодирования слова с заключается в поиске того смежного класса, к которому относится слово с = е + b . Вектор ошибок е определяет число и локализацию ошибок, кодовое слово b определяет коррекцию принятого слова.
Чтобы облегчить поиск смежного класса и тем самым вектора ошибок, Хемминг предложил использовать групповые коды со специальными порождающими матрицами.
Хемминговы коды
Рассмотрим построение хеммингова (т , п )-кода с наименьшим весом кодового слова равным 3, т. е. кода, исправляющего одну ошибку.
Положим п = 2 r– 1 и пусть в каждом кодовом слове будут r символов контрольными, а т символов (т = п – r = 2 r– 1– r ) — информационными, r ≥ 2, например (1, 3)-код, (4, 7)-код и т. д. При этом в каждом кодовом слове b = b 1b 2. b псимволы с индексами, равными степени 2, будут контрольными, а остальные информационными. Например, для (4, 7)-кода в кодовом слове b = b 1b 2b 3b 4b 5b 6b 7 символы b 1b 2b 4будут контрольными, а символы b 3b 5b 6b 7— информационными. Чтобы задать порождающую матрицу G хеммингова (т , п )-кода, рассмотрим вспомогательную матрицу М порядка r × п , где п = 2 r– 1, такую, что в каждом j столбце матрицы М будут стоять символы двоичного разложения числа j , например для (4, 7)-кода матрица М будет 3 × 7:
Множество всех кодовых слов зададим как множество решений однородной системы линейных алгебраических уравнений вида
Например, для (4, 7)-кода такая система будет:
Выберем естественный базисный минор системы b МТ= 0, стоящий в столбцах с номерами, равными степени 2. Тем самым переменные разделим на базисные (кодовые) и свободные (информационные). Теперь, задав свободные переменные, легко получить базисные. Найдем фундаментальную систему m = п – r решений этой однородной системы. Тогда любое решение системы есть линейная комбинация этих m решений. Поэтому, выписав построчно m решений фундаментальной системы в виде матрицы G размером m × п , получим порождающую матрицу хеммингова группового (т , п )-кода, например для (4, 7)-кода фундаментальной системой решений будут 4 = 7 – 3 следующих решения однородной системы:
g 1= 1110000, g 2= 1001100, g 3= 0101010, g 4= 1101001.
Любая линейная комбинация этих решений будет решением, т. е. кодовым словом. Составим из этих фундаментальных решений порождающую матрицу
Теперь по любому слову а длиной т = 4 легко вычислить кодовое слово b длиной п = 7 при помощи порождающей матрицы b = aG . При этом символы b 3, b 5, b 6, b 7будут информационными. Они совпадают с а 1, а 1, а 3, а 4.Символы b 1, b 2, b 4 будут контрольными.
Вывод . Хемминговы коды удобны тем, что при декодировании легко определяются классы смежности. Пусть принятое по каналу связи слово будет с = е + b , где е — ошибка, b — кодовое слово. Тогда умножим его на вспомогательную матрицу сМТ= (е + b )МТ= еМ T. Если еМ T= 0, то слово с — кодовое и считаем: ошибки нет. Если еМ T≠ 0, то слово е определяет ошибку.
Напомним, что построенный хеммингов (т , п )-код определяет одну ошибку. Поэтому вектор ошибки е содержит одну единицу в i позиции. Причем номер i позиции получается в двоичном представлении как результат еМ T, совпадающий с i столбцом матрицы М . Осталось изменить символ i в принятом по каналу слове с, вычеркнуть контрольные символы и выписать декодированное слово.
Например, пусть принятое слово будет с = 1100011 для (4, 7)-кода Хемминга. Умножим это слово на матрицу М T. Получим
Следовательно, есть ошибка во втором символе. Поэтому кодовое слово будет b = 1000011. Вычеркнем контрольные символы b 1, b 2, b 4.Декодированное слово будет а = 0011.
Конечно, если ошибка была допущена более чем в одном символе, то этот код ее не исправит.
💥 Видео
Коды, исправляющие ошибкиСкачать

ДМ 1 курс - 9 лекция - коды, исправляющие ошибки, границы Хэмминга и Гильберта, код ХэммингаСкачать

Занятие 34. Код Хэмминга (7,4) и его применениеСкачать

Код Хэмминга. Коррекция ошибокСкачать

Лекция 218. Код ХеммингаСкачать

Помехоустойчивое кодированиеСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Алексеев В. Б. - Дискретная математика - Коды ХэммингаСкачать

Код ХэммингаСкачать

Видеоурок "Расстояние между прямыми в пространстве"Скачать

Гашков С. Б. - Дискретная математика. Семинары - Код ХеммингаСкачать

Разбор алгоритма 461. Hamming DistanceСкачать