Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
рассмотрели три основные операции векторного анализа: вычисление gradtx для скалярного поля а и rot а для векторного поля а = а(ж, у, г). Эти операции могут быть записаны в более простом виде с помощью символического оператора V («набла»): Оператор V (оператор Гамильтона) обладает как дифференциальными, так и вектор- ными свойствами.
Формальное умножение, например, умножение ^ на функцию и(х, у), будем понимать как частное дифференцирование: В рамках векторной алгебры формальные операции над оператором V будем проводить так, как если бы он был вектором. Используя этот формализм, получим следующие основные формулы: 1.
Если — скалярная дифференцируемая функция, то по правилу умножения вектора на скаляр получим где P, Q, R — дифференцируемые функции, то по формуле для нахождения скалярного произведения получим Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 3.
Вычисляя векторное произведение [V, а], получим Для постоянной функции и = с получим а для постоянного вектора с будем иметь Из распределительного свойства для скалярного и векторного произведений получаем Замечание 1. Формулы (5) и (6) можно трактовать тамке как проявление дифференциальных свойств оператора «набла» (V — линейный дифференциальный оператор). Условились считал., что оператор V действует на все величины, написанные за ним.
В этом смысле, например, — скалярный дифференциальный оператор.
Применяя оператор V к произведению каких-либо величин, надо иметь в виду обычное правило дифференцирования произведения. Пример 1. Доказать, что По формуле (2) с учетом замечания 1 получаем или Чтобы отметить тот факт, что «набл а» не действует на какую-либо величину, входящую в состав сложной формулы, эту величину отмечают индексом с («const»), который в окончательном результате опускается. Пример 2.
Пусть u(xty,z) — скалярная дифференцируемая функция, а(х,у,г) — векторная дифференцируемая функция. Доказать, что 4 Перепишем левую часть (8) в символическом виде Учитывая дифференциальный характер оператора V, получаем . Так как ие — постоянный скаляр, то его можно вынести за знак скалярного произведения, так что а (на последнем шаге мы опустили индекс е). В выражении (V, иас) оператор V действует только на скалярную функцию и, поэтому В итоге получаем Замечай ие 2.
Используя формализм действа с оператором V как с вектором, надо помнить, что V не является обычным вектором — он не им«ет ни длины, ни направления, так что. например, вектор [V,aJ не будет, вообще говоря, перпендикулярным вектору а (впрочем, для плоского поля вектор перпендикулярен плоскости ,а значит, и вектору а).
Возможно вам будут полезны данные страницы:
Не имеет смысла и понятие коллинеарности по отношению к символическому вектору V. Например, выражение , где V и ^ — скалярные функции, формально напоминает векторное произведение двух коллинеарных векторов, которое всегда равно нулю. Однако вобшем случае это не имеет места. В самом деле, вектор = grad направлен по нормали к поверхности уровня , а вектор Vy = grad t> определяет нормаль к поверхности уровня i> = const.
| Вобшем случае эти нормали не обязаны |
быть коллннеарнымн (рис. 40). С другой стороны, в любом дифференцируемом скалярном поле ) имеем Эта примеры показывают, что с оператором «набла» нужно обращаться с большой осторожностью и при отсутствии уверенности в полученном результате его следует проверить аналитическими методами. §12. Дифференциальные операции второго порядка. Оператор Лапласа Дифференциальные операции второго порядка получаются в результате двукратного применения оператора V. 1.
- Скалярное поле
- Цилиндрические координаты
- Сказ царя Салтана о потенциале лапласиана
- 1. Уравнение баланса
- Баланс потенциалов
- Рейтинги и самооценки
- 2. Лапласианы
- Потенциалы лапласианов
- Как считать потенциалы больших графов
- Ранжирование объектов на основе потенциалов и потоков
- Результаты турниров
- Потенциалы пьяницы
- Заключение
- Использование оператора набла для записи операции взятия дивергенции.
- Выражение div E в цилиндрической и сферической системах координат.
- Уравнение Пуассона и уравнение Лапласа.
- 💥 Видео
Скалярное поле
В этом поле оператор V порождает векторное поле В векторном поле grad и можно определить две операции: что приводит к скалярному полю, и что приводит к векторному полю. 2. Пусть задано векторное поле . Тогда оператор V порождает в нем скалярное поле В скалярном поле div а оператор V порождает векторное поле 3.
В векторном поле оператор V порождает также векторное поле Применяя к этому полю снова оператор V, получим: а) скалярное поле Выберем в пространстве прямоугольнуюдекартову систему координат Oxyz и рассмотрим каждую из формул (1)-(5) более подробно. 1. Предполагая, что функция имеет непрерывные вторые частные производные , получим Символ называется оператором Лапласа, или лапласианом. Его можно представить как скалярное произведение оператора Гамильтона V на самого себя,т. е. Оператор Д (дельта) играет важную роль в математической физике.
Уравнение называется уравнением Лапласа. С его помощью описывается, например, стационарное распределение тепла. Скалярное поле и, удовлетворяющее условию , называется лапла-совым или гармоническим полем. Например, скалярное поле является гармоническим во воем трехмерном пространстве: из того, что получаем Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты 2.
Пусть функция и имеет непрерывные частные производные второго порядка включительно. Тогда В самом деле, действуя формально, получим ибо как векторное произведение двух одинаковых «векторов». Tor же результат можно получить, используя выражения градиента и ротора в декартовых координатах Пусть задано векторное поле координаты которого P, Q, R имеют непрерывные частные производные второго порядка. Тогда получим 4. При тех же условиях, что и в пункте 3, имеем Это соотношение уже было доказано ранее путем непосредственных вычислений.
Здесь мы приведем его формальное доказательство, используя известную формулу из векторной алгебры Имеем как векторное произведение двух одинаковых «векторов». 5. Покажем, наконец, что при тех же условиях, что и ранее, Так как то, полагая в формуле для двойного векторного произведения получим Поэтому окончательно будем иметь где grad diva выражается по формуле (8), а Да для вектора надо понимать так:. В заключение приведем таблицу дифференциальных операций второго порядка. Скалярное поле Векторное поле Заштрихованные прямоугольники означают, что соответствующая операция не имеет смысла (например, градиент от. § 13.
Понятие о криволинейных координатах Во многих задачах бывает удобно определять положение точки пространства не декартовыми координатами ), а тремя другими числами (qh 42,4з), более естественно связанными с рассматриваемой части ой задачей. Если задано правило, согласно которому каждой точке М пространства отвечает определенная тройка чисел и, обратно, каждой такой тройке чисел отвечает единственная точка М, то говорят, что в пространстве задана криволинейная координатная система.
В этом случае величины ф, называют криволинейными координатами точки М. Координатными поверхностями в системе криволинейных координат qtqi, Яз называются поверхности На координатных поверхностях одна из координат сохраняет постоянное значение. Линии пересечения двух координатных поверхностей называются координатными линиями. В качестве примеров криволинейных координат рассмотрим цилиндрические и сферические координаты. 13.1.
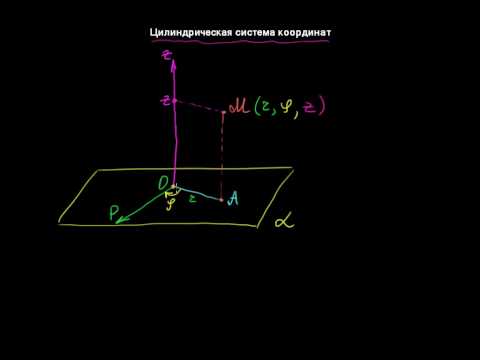
Цилиндрические координаты
В цилиндрических координатах положение точки М в пространстве определяется тремя координатами: (р = const — полуплоскости, примыкающие к оси Oz z = const — плоскости, перпендикулярные оси Oz (рис. 41). Координатные линии: 1) линии (р) — лучи, перпендикулярные оси Oz и имеющие начало на этой оси, т.е. линии пересечения координатных поверхностей у? = const, z = const; 2) линии (ip) — окружности с центрами на оси Oz, лежащие в плоскостях, перпендикулярных оси Oz 3) линии (z) — прямые, параллельные оси Связь декартовых координат точки с цилиндрическими координатами ( задается формулами 13.2.
Сферические координаты В сферических координатах положение точки Af в пространстве определяется следующими координатами: Координатные поверхности (рис.42): г = const — сферы с центром в точке О; • в = const — круговые полуконусы с осью полуплоскости, примыкающие к оси Oz. Координатные линии: 1) линии (г) — лучи, выходящие източки О; 2) линии (в) — меридианы на сфере; 3) линии — параллели на сфере. Связь декартовых координат (х, у, z) точки М с ее сферическими координатами задается формулами.
Введем единичные векторы (орты), направленные по касательным к коор-динатнымлиниям вточке М всторонувозрастанияпеременных qx, q2, соответствен но. Определение. Система криволинейных координат называется ортогональной, если в каждой точке М орты попарно ортогональны. В такой системе ортогональны и координатные линии, и координатные поверхности. Примерами ортогональных криволинейных координат служатсистемы цилиндрических и сферических координат.
Мы ограничимся рассмотрением только ортогональных систем координат. Пусть — радиус-вектор точки М — Тогда можно показать, что Оператор Гамильтона Дифференциальные операции второго порядка Оператор Лапласа Понятие о криволинейных координатах Сферические координаты Аналогично для сферических координат имеем Величины являются дифференциалами длин дуг соответс твующих координатных линий.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Оператор Лапласа в криволинейных координатахСкачать

Сказ царя Салтана о потенциале лапласиана
«Три девицы под окном пряли поздно вечерком.»
Ну как пряли. Не пряли, конечно, а лайкали друг на друга. По условиям конкурса «мисс Салтан» девицы должны были выбрать меж собой лучшую.
«Какой-то странный конкурс», — беспокоились девицы. И это было правдой. По правилам конкурса вес лайка участника зависел от того, сколько лайков он получает от других. Что это значит, — никто из девиц до конца не понимал.
«Как все сложно», — тосковали девушки и подбадривали себя песней «Кабы я была царицей».
Вскоре «в светлицу вошел царь — стороны той государь» (показан на рисунке). «Во все время разговора. », — ну понятно в общем.
«Собираем лайки нежности — формируем матрицу смежности», — бодро срифмовал он.
Девицы-красавицы с именами Алена, Варвара и Софья засмущались, но лайки (из балалайки) передали.
Вот что там было:
- Алена получила 1 лайк от Софьи и 2 лайка от Варвары.
- Варвара получила по лайку от Алены и Софьи.
- А Софья получила 2 лайка от Алены и 1 от Варвары.
Царь взял лайки, покрутил гайки, постучал по колесам, пошмыгал носом, причмокнул губами, поскрипел зубами, сгонял в палаты и объявил результаты.
Наибольший вес лайков (7 баллов) получила Софья, но титул «мисс Салтан» достался Алене (15 баллов).
Для матрицы
вектор потенциалов равен (5, 4, 7), а вектор потоков — (15, 12, 14).
После объявления результатов девицы бросились обратились к царю с просьбой рассказать,- откуда взялись эти странные цифры?
Видео:Оператор набла (оператор Гамильтона) и оператор ЛапласаСкачать

1. Уравнение баланса
В основе нашего мира лежит баланс. Это означает, что если в одном месте что-то прибыло, то в другом месте столько же убыло.
Физики демонстрируют данный баланс уравнением непрерывности для сплошных и непрерывных сред. Но в современном мире рулят танковые клинья дискретные системы — графы.
У графа есть узлы, через которые течет поток (ну как течет — толчками и нерегулярно). Принцип баланса прост — в узле графа остается разница между тем, сколько из него вытекло и сколько в него втекло. А куда течет поток из узла? Правильно — в другие узлы, соответственно втекает поток в узел тоже из других узлов.
Запишем это множество слов формулой:
Здесь обозначает количество входящего потока в i-й узел,
— количество исходящего из узла потока,
— изменение остатка в узле.
Да, остатки в наших кошельках подчиняются данному уравнению баланса. И весь бухгалтерский учет на нем основан, — даже названия специальные придумали: исходящий поток — кредит, входящий — дебет.
Неизвестно, кто и почему ввел принцип баланса в естественные (физические) системы, но в основу искусственных систем (учет, рейтинги, кармы и пр.) лучше закладывать принцип баланса. Если мир выжил на балансе, то и у такой системы есть шанс.
В многих ситуациях (в частности с нашим конкурсом оценок) учет остатка в узле не нужен. То есть он всегда нулевой — сколько втекло — столько и вытекло. Игра с нулевой стоимостью нулевым остатком. Для таких систем уравнение упрощается:
Круто. Но пока малополезно.
Баланс потенциалов
Когда мы говорили о том, что поток может течь из узла i в узел j, мы подразумевали, что есть некая связь между данными узлами. Иначе потоку просто не по чему течь. Связность узлов графа обычно называют матрицей смежности (связности), ее элементы обозначают через . Применительно к потокам матрицу смежности также называют матрицей проводимости. Ее элементы отражают пропускную способность ребер графа.
Есть связь — есть поток, нет связи — нет потока. Логично предположить, что чем сильнее связь — тем больше поток.
Итак, поток между узлами пропорционален величине связи узлов. Но чему равен коэффициент пропорциональности?
Ответ будет немного туманный — поток из узла пропорционален некоему потенциалу узла.
Суть данного ответа в том, что узлы обладают неким потенциалом и данный потенциал непосредственно определяет величину исходящего потока. Если, например, у нас есть два узла, проводимость между которыми одинакова в обоих направлениях (
), то суммарный поток между узлами будет определяться разностью потенциалов данных узлов. Существование электрических сетей доказывает, что это реально работает.
Связь потока с потенциалами и проводимостью выражается простой формулой:
Подставляя (1.3) в уравнение баланса (1.2) получаем систему уравнений для расчета потенциалов узлов:
В данном уравнении известными являются проводимости, а неизвестными — потенциалы.
Количество уравнений в системе равно количеству узлов графа. Решение системы балансовых уравнений является прямой задачей расчета потенциалов (и потоков) графа.
В уравнении (1.4) мы использовали понятие общей проводимости исходящих из узла связей — степень узла:
Рейтинги и самооценки
«Все это здорово,» — сказали девушки, зевая. — «Но причем тут лайки?»
В системах голосования, при которых участники оценивают друг друга, оценки берутся с учетом веса голоса каждого участника. А вес голоса опять же зависит от того, как данного участника оценили другие.
Связываем с потоками. Когда i-й участник с весом голоса оценивает j-го участника с оценкой (количеством лайков)
то он делится с ним своим потоком
. Копить остатки тут ни к чему, поэтому каждый участник делится с остальными всем, что получил.
Вес голоса участника — это потенциал , матрица лайков — это матрица смежности (связности), а итоговая оценка — суммарный полученный (он же отданный) поток
.
Для ранжирования участников (определения лучших) нам надо решить уравнение баланса (1.4), то есть определить веса участников, которые сбалансируют систему.
Видео:Оператор Лапласа в полярных координатахСкачать

2. Лапласианы
Когда я был молодым и глупым впервые столкнулся с уравнением баланса (1.4), я уже умел программировать и знал про циклы. Поэтому решал его как программист — методом последовательных итераций. Задаем начальный вектор потенциалов, умножаем его на матрицу смежности, делим на степени узлов, получаем новый вектор потенциалов и т. д. Как правило, процесс сходится. А вспомнил я про молодость, прочитав статью о ценностях пьяницы, которая в общем и побудила меня «расчехлить формулы».
Помню «вау-эффект», когда я узнал о том, что есть и другой способ расчета потенциалов, о котором, видимо, знали еще наши деды Лаплас и Кирхгоф. Способ основывается на свойствах матриц-лапласианов. Тут уже недавно вспоминали лапласианы в непрерывных средах. Дискретные лапласианы не менее интересны и важны.
Для того, чтобы определить матрицу лапласиана по заданной матрице смежности, используем веденное выше понятие степени узлов. Степени узлов расположим по диагонали лапласиана, а остальные элементы возьмем из матрицы смежности с обратным знаком. Получившуюся матрицу называют также матрицей Кирхгофа:
Примем, что проводимость исходящих из узла i дуг задается в i-м столбце матрицы. Соответственно в i-й строке матрицы – проводимость входящих в узел дуг. Тогда сумма элементов каждого столбца лапласиана равна нулю.
Вообще говоря, матрицы данного вида образуют отдельный класс, — лапласианы. Определитель лапласианов всегда равен нулю, поэтому, например, для них не существует обычной обратной матрицы. Но зато есть другая (псевдо)обратная, есть и своя единичная матрица. Получить лапласиан можно не только приведенным выше преобразованием. Например, преобразование девиации тоже дает лапласиан на выходе.
Лапласианы могут быть симметричными — в них потенциалы всех узлов равны между собой — для нашей задачи они пока неинтересны.
Матрица Кирхгофа относится к классу лапласианов.
Потенциалы лапласианов
В линейной алгебре есть понятие дополнительного минора (кофактора) матрицы — это определитель матрицы, полученной из исходной вычеркиванием строк и столбцов (с учетом знака). Кофакторы играют большую роль в лапласианах.
Потенциалом 1-го порядка лапласиана называется определитель матрицы, полученный вычеркиванием из исходного лапласиана одной строки и одного столбца.
Поскольку мы приняли, что в наших лапласианах сумма каждого столбца нулевая, то значение потенциала определяется только вычеркнутой колонкой, — строка может быть любой. Удобно вычеркивать ту же строку, что и колонка, — тогда не надо думать о знаке определителя.
Итак, если обозначить через дополнительный минор матрицы, то определение потенциала лапласиана можно записать как
Так вот эти потенциалы 1-го порядка от матрицы Кирхгофа и являются искомым решением уравнения (1.4).
Удивительно. Не нужны никакие циклы, начальные присваивания, произведение матриц и пр. Удалил строку/колонку, посчитал определитель — получил ответ.
- Потенциал узла представляет собой сумму произведений (кортежей) проводимостей ребер графа по всем возможным путям в данный узел, исключая контуры (циклы).
- Количество множителей в произведении на 1 меньше размерности (количества узлов) графа.
- Потенциал узла не зависит от проводимостей исходящих из него дуг.
- Каждый кортеж (путь) в выражении для потенциала узла состоит из дуг, которые исходят из всех узлов, кроме данного. В одном кортеже нет двух дуг, исходящих из одного узла, но могут быть дуги, входящие в один узел.
- В каждом кортеже (пути) обязательно присутствует дуга, входящая в узел (замкнутость).
- В выражении для потенциала отсутствуют кортежи, содержащие циклы (контуры).
- Количество кортежей в выражении для потенциала определяется известной формулой Кэли
, и быстро растет с ростом узлов графа. Для 4-х узлов имеем 4^2 = 16 слагаемых, для пяти — 5^3 = 125 и т. д.
- В симметричном графе потенциалы всех узлов равны – следствие того, что структура выражения для потенциалов всех узлов одна и та же (разница лишь в направлении).
Для определения потока через узел достаточно умножить потенциал узла на его степень:
Мы получили, что хотели.
Для расчета веса голоса (потенциала) участника вычеркиваем соответствующую строку и столбец и считаем определитель. Получаем 3 потенциала:
Это вес голоса каждого участника. Теперь считаем потоки и определяем, кто сколько голосов набрал:
Алена набрала больше всех голосов.
Как считать потенциалы больших графов
Если граф большой (много узлов), то считать вектор потенциалоф через вычисление определителей миноров лапласиана неудобно (затратно). В таких ситуациях лучше использовать обращение матрицы. Алгоритм следующий:
- В матрице лапласиана заменяем первую строку на вектор (1, 0, 0, . ).
- Считаем обратную матрицу от полученной и находим ее детерминант.
- Делим значения первой колонки полученной обратной матрицы на ее детерминант. Это и есть искомый вектор потенциалов. В первой строке — потенциал первого узла, во второй — второй и т. д.
- Если абсолютное значение потенциала неважно, то считать и делить на детерминант необязательно.
Видео:Сферические координатыСкачать

Ранжирование объектов на основе потенциалов и потоков
По итогам нашего примера получилось так, что наибольший вес голоса получила Софья, но больше всего баллов набрала Алена.
Это означает, что авторитетные и избранные — это не одно и тоже.
Что именно должно служить основанием для ранжирования, — потенциалы или потоки,- требует отдельного рассмотрения в каждой задаче, поскольку определяется прикладным аспектом.
Результаты турниров
Рассмотрим применение системы ранжирования применительно к определениям итогов шахматного турнира. Справедлива ли нынешняя система определения победителя простой суммой очков? На наш взгляд, она имеет лишь одно достоинство — простота. Но в век смартфонов кого волнует простота?
Несправедливо то, что выигрыш сильного по сути приравнивается в «простой системе» выигрышу у слабого.
Современный и правильный подход — считать взвешенные очки, то есть использовать расчет потенциалов и потоков. Еще один плюс — при данной системе практически исключена дележка мест — не надо думать о том, что делать при равенстве очков.
Как раз недавно в Москве закончился турнир претендентов (поздравляем Сергея Карякина с победой!), по итогам которого большое количество участников поделило места (2-3, 4-7). Используя метод потенциалов, попробуем разобраться, кто же какое место занял на самом деле.
Результаты турнира — это матрица смежности графа. В терминах лайков проигрыш участника — это проставление лайка победителю (хотя и звучит немного непривычно). От проигравшего к победителю идет поток взвешенных очков.
А что такое потенциал применительно к игрокам?
Потенциал — это показанная участником сила игры (в данном турнире). Чем выше потенциал участника — тем большую ценность имеют очки, полученные от него другими.
Возможно ли, чтобы менее сильный игрок набрал большее количество очков, чем более сильный? Да, такое вполне возможно, хоть и бывает не так часто. Например, на упомянутом турнире претендентов сила участника и набранные им очки совпали — ранжирование по потенциалам и потокам оказались эквивалентными.
Мы нормировали потенциалы и потоки так, чтобы их сумма была равна 100.
| Сергей Карякин | Хикару Накамура | Аниш Гири | Виши Ананд | Веселин Топалов | Левон Аронян | Фабиано Каруана | Петр Свидлер | |
| U | 17,8 | 11,4 | 12,5 | 13,7 | 6,4 | 12,0 | 13,8 | 12,4 |
| J | 14,5 | 11,8 | 13,0 | 13,2 | 9,0 | 12,4 | 13,3 | 12,8 |
| М | 1 | 7 | 4 | 3 | 8 | 6 | 2 | 5 |
Каруана все-таки второй, а Гири — 4-й.
Потенциалы пьяницы
Последний пример, который мы рассмотрим в данной статье — это расчет ценности карт в народной игре «Пьяница».
Спасибо за данный пример astgtciv. Без его статьи, возможно, не было бы и этой.
Подробности о постановке задачи есть в упомянутой статье, — карты бьют друг друга по правилам старшинства, но при этом шестерка бьет туза.
Данная задача хороша тем, что значения потенциалов (хм, а потоки тут что означают?) могут быть выражены в явном виде — несложными формулами.
Общий вид матрицы смежности соответствует результатам карточных сравнений — кто кого бьет.
Нумеруя карты от условного туза к условной шестерке, получаем следующий вид матрицы смежности:
Ключевая особенность — в левом нижнем (и/или правом верхнем) углу — «шестерка бьет туза».
Тогда матрица Кирхгофа будет иметь вид:
Теперь наглядно видно, почему потенциал «шестерки» равен (n-2)! Потому что вычеркнув колонку и строку, соответствующие «шестерке» (это крайние ряды справа и снизу), мы получаем треугольную матрицу, определитель которой считается простым умножением элементов главной диагонали.
То же самое справедливо и для туза (1-я строка и колонка) с той лишь разницей, что у него в составе множителей два раза встречается элемент (n-2). Поэтому сразу видно, что потенциал туза всегда в (n-2) раза больше потенциала шестерки.
Выражения для потенциалов от туза до шестерки:
Интересно, что сумма потенциалов всех карт (кроме шестерки и туза) равна потенциалу туза:
Заключение
Сколько могли старались и слушали девицы сказ царя Салтана про возможности лапласиана, да все равно сморил их крепкий сон.
Снились им добры-молодцы с большим потенциалом, управляющие крупными потоками.
Пришла и нам пора закругляться. Используйте потенциалы!
Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Использование оператора набла для записи операции взятия дивергенции.
Ранее было показано, что умножение оператора V на скалярную функцию равносильно взятию градиента от этой скалярной функции. Покажем, что скалярное умножение оператора V на векторную функцию, например, на функцию ?, означает взятие дивергенции от этой векторной функции.
Произведение V ? можно записать так:
Правые части (19.22) и (19.23) равны, следовательно, должны быть равны и левые. Поэтому V? = div?, т. е., действительно, умножение оператора V на вектор ? означает взятие дивергенции от этого вектора.
Видео:Оператор момента в сферических координатахСкачать

Выражение div E в цилиндрической и сферической системах координат.
Без вывода запишем выражение div Ё:
в цилиндрической системе координат
в сферической системе координат:
Видео:§56 Сферическая система координатСкачать

Уравнение Пуассона и уравнение Лапласа.
Эти уравнения являются основными дифференциальными уравнениями электростатики. Они вытекают из теоремы Гаусса в дифференциальной форме. Действительно, известно, что ? = -grad(p. В то же время согласно теореме Гаусса (19.21) div? = рск6/е,.
’> Почленно умножаем слагаемые первой скобки на слагаемые второй скобки. Учитываем, что скалярное _произведение одноименных_ ортов, равно единице, а разноименных — нулю: i 1 = j j = к к -1 1 cosO 0 = 1, / j = 7 к = j к = 1 • 1 — cos90° = 0.
Подставим в (19.21) Е из (19.6), получим 
Вместо grad(p запишем его эквивалент V ср; вместо div напишем V . Тогда
Уравнение (19.26) называют уравнением Пуассона. Частный вид уравнения Пуассона, когда рС50б = 0, называют уравнение Лапласа. Уравнение Лапласа записывают так:
Оператор V 2 = div grad называют оператором Лапласа, или лапласианом, и иногда обозначают еще символом Д. Поэтому можно встретить и такую форму записи уравнения Пуассона:
💥 Видео
Объем через тройной интеграл в сферической системе координатСкачать

Скорость и ускорение точки в полярных координатахСкачать

Техническая механика/ Определение равнодействующей. Плоская система сходящихся сил.Скачать

Урок 5. Решение уравнения Лапласа в сферических координатахСкачать

Как понимать параметры круговой интерполяцииСкачать

Демидович №4415.1б: градиент в сферических координатахСкачать

Оператор ЛапласаСкачать

КОРРЕКЦИЯ БЕЗ ОПИЛА ПОВЕРХНОСТИ/ форма квадратСкачать

Теория поля_семинар-5. Дифференцирование в сферических координатах.Скачать

#2.27 Berkeley / Беркли Лапласиан в сферических координатах / Laplace Operator in Spherical CoordsСкачать

§55 Цилиндрическая система координатСкачать
Сферические координаты и координатные линииСкачать

Полярная система координатСкачать

















