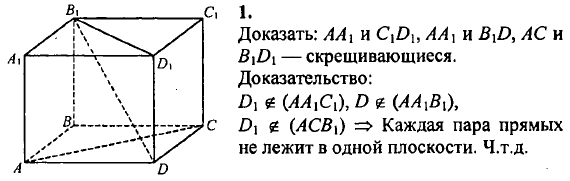Дан куб являются ли параллельными прямые аа1 и dd1 аа1 и сс1 ответ обоснуйте

1) ввести определение скрещивающихся прямых;

2) ввести формулировку и уметь доказать признак и свойство скрещивающихся прямых.

I. Организационный момент

Сообщить тему урока, сформулировать цели урока.

II. Анализ самостоятельной работы

Сообщение итогов работы, анализ распространенных ошибок.

III. Изучение нового материала

Были рассмотрены два случая расположения прямых в пространстве. (a ∩ b; а || b). Общее для них: они лежат в одной плоскости (рис. 1, 2).

(по следствию из аксиомы)

(по определению параллельных прямых)

Дан куб ABCDA1B1C1D1 (рис. 3).

1. Являются ли параллельными прямые А1А и DD1; АА1 и CC1? Ответ обоснуйте. (А1А || DD1 как противоположные стороны квадрата или лежат в одной плоскости и не пересекаются). (А1А || DD1 и DD1 || CC1 ⇒ A1A || CC1 по теореме о трех параллельных прямых).

2. Являются ли АА1 и DC параллельными? Они пересекаются? Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Обратить внимание учеников на то, что условие «не лежат в одной плоскости» означает, что не существует плоскости, содержащей эти прямые. Именно на этом построено доказательство признака скрещивающихся прямых.

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).

Доказать, что АВ скрещивается с CD.

Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.

Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.

Закрепление изученной теоремы (с устным обоснованием) (рис. 5).

1. Определить взаимное расположение прямых АВ1 и DC. (АВ, скрещивается c DC.)

2. Указать взаимное расположение прямой DC и плоскости АА1ВВ1. (DC || плоскости АА1ВВ1.)

3. Является ли прямая АВ1 параллельной плоскостиDD1CC1? (Да.)

При обсуждении 2 и 3 задания обратить внимание на существование плоскости, проходящей через одну из скрещивающихся прямых и параллельной другой прямой.

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.

Дано: АВ скрещивается CD (рис. 6).

Построить α: АВ ⊂ α, CD || α.

Доказать, что α — единственная.

1. Через точку А проведем прямую АЕ, АЕ || CD.

2. Прямые АЕ и АВ пересекаются и образуют плоскость α. АВ ⊂ α (по построению), CD || α (по признаку параллельности прямой и плоскости), α — искомая плоскость.

3. Докажем, что α — единственная плоскость. α — единственная по следствию из аксиом. Любая другая плоскость, которой принадлежит АВ, пересекает АЕ и, следовательно, прямую CD.

Обратить внимание учащихся, что в доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.

Построить плоскость α, проходящей через точку К и параллельной скрещивающимся прямым а и b (рис. 7).

1. Через точку К провести прямую а’ || а. (прямая а и точка К определяют плоскость; построение возможно и а’ — единственная прямая).

2. Через точку К провести прямую b’ || b.

3. Через пересекающиеся прямые проведем плоскость α. α — искомая, единственная плоскость.

IV. Закрепление изученного материала

1. Решение задач № 34 и 39 на доске и в тетрадях.

Дано: D ∈ плоскости ABC. АМ = MD; DN = NB; DP = PC; К ∈ BN (рис. 8).

Определить взаимное расположение прямых:

а) ND и АВ. ND ∩ АВ = В (D, А, N и В лежат в одной плоскости и );

б) РК и ВС. РК ∩ ВС = P1 (К, Р, С, В лежат в одной плоскости и );

в) MN и АВ. MN || АВ (по свойству средней линии треугольника MN || АВ);

г) МР и АС. МР || АС (по свойству средней линии треугольника МР || АС);

д) KN и AC. KN ∩ плоскости ADC = D; D ∉ АС ⇒ KN скрещивается с АС по признаку скрещивающихся прямых;

е) MD и ВС; MD ∩ плоскости ABC = A, A ∉ ВС ⇒ MD скрещивается с ВС по признаку скрещивающихся прямых.

Дано: АВ и CD скрещиваются (рис. 9).

Доказать, что AD и ВС скрещиваются.

1. Точка А, С, D лежат в одной плоскости (по аксиоме A1). Пусть эта плоскость α.

2. В g α, так как АВ и CD скрещиваются (по определению скрещивающихся прямых).

3. ВС ∩ α = С; С ∉ AD ⇒ AD и ВС скрещиваются (по признаку скрещивающихся прямых).

2. Самостоятельно решить задачи с последующей проверкой: № 93, 94.

Дано: а || b. MN ∩ а = М (рис. 10).

Определить взаимное расположение прямых MN и b.

1. a || b ⇒ существует плоскость α, проходящая через а и b.

2. MN и b скрещиваются (по признаку скрещивающихся прямых). (Ответ: MN и b скрещиваются.)

Дано: а скрещиваются Ь. В ∉ а и В ∉ b (рис. 11).

Определить взаимное расположение плоскостей α и β. α проходит через прямую а и точку В. β проходит через прямую b и точку В. α ∩ β, так как плоскости имеют одну общую точку и по аксиоме А3 они пересекаются и точка В принадлежит линии пересечения.

V. Подведение итогов

Плоскости α и β пересекаются по прямой l, которая является скрещивающейся с прямой а.

Докажите, что прямая а пересекает хотя бы одну из плоскостей α и β.

№ 35. Предположим, что а и b не скрещиваются ⇒ а || b или а ∩ b. Через а и b проведем плоскость β. Предположим, что а не скрещиваются с ⇒ а || с или а ∩ с. Через прямые а и с проведем плоскость γ. а — линия пересечения плоскостей β и γ. что противоречит условию.

Следовательно, а и b скрещиваются или а и с скрещиваются.

№ 36. а || b ⇒ существует плоскость α (рис. 13), которой принадлежат эти прямые, b и с скрещиваются по признаку скрещивающихся прямых.

№ 37 (рис. 14, рис. 15).

а) Рис. 14. (по свойству параллельных прямых).

б) Рис. 15, m ∩ АВ = М, АВ ⊂ плоскости ABC ⇒ m ∩ плоскости ABC = М. m и ВС скрещиваются по признаку скрещивающихся прямых.

Пусть (рис. 16). Возьмем любую точку М на прямой l.

Через прямую а и М проведем плоскость γ.

так как (по А3).

так как (по А3).

Итак, чего быть не может, т. к. Следовательно, а ∩ α или а ∩ β.

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Конспект урока по геометрии 10 класс

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Урок геометрии в 10 классе по теме «Параллельные прямые в пространстве»

— рассмотреть взаимное расположение двух прямых в пространстве;

— ввести понятие параллельных и скрещивающихся прямых;

— совершенствовать навыки решения геометрических задач.

— осуществлять пропедевтику формирования интеллектуально-информационных умений;

— формировать умения обобщать, систематизировать;

— развивать самостоятельность в мышлении и учебной деятельности.

— воспитывать интерес к предмету;

— воспитывать ответственность, самостоятельность, уважительное отношение друг к другу.

Тип урока: комбинированный – объяснение нового материала

Формы учебной работы учащихся: фронтальная работа, индивидуальная работа.

Оборудование: компьютер с мультимедийным проектором.

(В ходе урока используется презентация Microsoft PowerPoint «Параллельные прямые в пространстве»)

2. Объяснение нового материала.

1). Каково может быть взаимное расположение двух прямых на плоскости?

( Ответ : совпадают, пересекаются, параллельны .)

2). Дайте определение параллельных прямых на плоскости.

(Ответ: Параллельными называются прямые, лежащие в одной плоскости и не пересекающие друг друга.)

2. Изучение нового материала.

Рассмотрение текста учебника. Беседа. Вывод: Параллельными прямыми в пространстве называются прямые, лежащие в одной плоскости и не пересекающие друг друга.

3). Дан куб. Являются ли параллельными прямые:

(Ответ: АА₁ и DD ₁ — параллельны, т.к. являются противоположными сторонами квадрата. АА₁ и СС₁ – параллельны, т.к. СС₁ параллельна DD ₁.)

2) АА₁ и D С? Они пересекаются?

(Ответ: АА₁ и D С не параллельны и не пересекаются.)

Значит, в пространстве есть прямые, которые не пересекаются, но и не являются параллельными. Такие прямые называются скрещивающимися.

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

4). По рисункам назовите:

1) пары скрещивающихся ребер;

2) пары параллельных ребер.

Итак, алгоритм распознавания взаимного расположения двух прямых в пространстве.

Возьмем две прямые а и в.

Определим: лежат ли они в одной плоскости.

Если нет, то прямые скрещивающиеся.

Если лежат, то определим: имеют ли они хотя бы одну общую точку.

Если нет, то прямые параллельны.

Если имеют, то определим: имеют ли данные прямые более одной общей точки.

Если нет, то прямые пересекаются.

Если прямые имеют более одной общей точки, то они совпадают.

3. Решение задач.

1). Всегда ли две непересекающиеся прямые в пространстве параллельны?

(Ответ: нет, прямые могут быть скрещивающимися)

2). Какие две прямые называются параллельными?

(Ответ: прямые, лежащие в одной плоскости и не пересекающие друг друга.)

3). Дано: а || в . Докажите, что все прямые, пересекающие данные лежат в одной плоскости.

(Ответ: любая прямая, пересекающая данные прямые, имеет две точки, принадлежащие плоскости, в которой лежат прямые а и в. Следовательно, она лежит в этой плоскости.)

4). Сколько можно провести в пространстве прямых, проходящих через данную точку, параллельных данной прямой?

(Ответ: только одну.)

4. Подведение итогов урока.

5. Домашнее задание. п. 4, №16, № 89.

1. Геометрия: Учебник для средней школы. 10–11 классы./ Под ред. Л.С. Атанасяна, В.Ф. Бутузова, С.Б. Кадомцева и др. – М.: Просвещение, 2014.

2. Геометрия. 10 класс. Поурочные планы / Авт.-сост. Г.И. Ковалева – Волгоград: Учитель, 2014

Видео:Найти в кубе угол между двумя прямымиСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 338 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 693 человека из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Иванова Надежда НиколаевнаНаписать 952 04.08.2019

Номер материала: ДБ-658817

31.07.2019 230

29.07.2019 702

27.07.2019 112

23.07.2019 265

19.07.2019 384

12.06.2019 125

03.06.2019 267

25.03.2019 267

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Во всех педвузах страны появятся технопарки

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Россия направит $10,3 млн на развитие школьного питания в нескольких странах

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:№557. Стороны угла А пересечены параллельными прямыми ВС и DE, причем точки В и D лежатСкачать

1. Докажите, что прямые АА1 и C1D1 АА1 и B1D, АС и B1D1 являются. 10 класс Зив Б.Г. Геометрия. Самостоятельная работа 2. Вариант 3

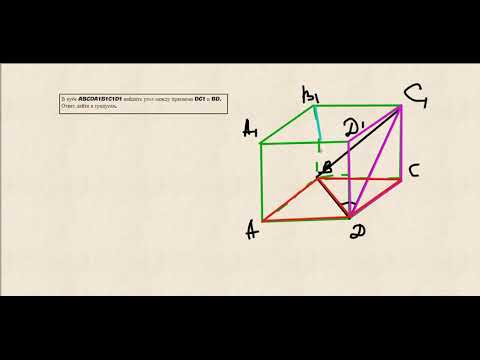
1. Докажите, что прямые АА1 и C1D1 АА1 и B1D, АС и B1D1 являются скрещивающимися (рис. 11).

ответ

Решите уровнения:
а)4x — 12 = 18 — x
б)21x — 5(2x-7)=24 ( Подробнее. )

a) Match the countries to the nationalities. Listen and check. What nationality are you?

b) Choose a flag and describe it ( Подробнее. )

1. ABCD — квадрат со стороной, равной √2, О — точка пересечения его диагоналей, ОЕ — перпендикуляр к плоскости АВС, ОЕ = √3. Найдите ( Подробнее. )

2. Основанием пирамиды PEFM служит равнобедренный треугольник, EF = ЕМ, MF = 20√6. Боковое ребро РЕ равно 10 и перпендикулярно ( Подробнее. )

🎥 Видео

Геометрия 7 класс (Урок№18 - Параллельные прямые.)Скачать

№190. Дан куб ABCDA1B1C1D1. Найдите следующие двугранные углы: а) АВВ1ССкачать

Угол между прямыми в пространстве. Практическая часть. 10 класс.Скачать

Угол между прямыми в пространстве. 10 класс.Скачать

Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

10 класс, 7 урок, Скрещивающиеся прямыеСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

№191. Дан куб ABCDA1B1C1D1. Докажите, что плоскостиСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. §13 геометрия 7 классСкачать

СЕЧЕНИЯ. СТРАШНЫЙ УРОК | Математика | TutorOnlineСкачать

Параллельные прямые (задачи).Скачать

Параллельность прямых. 10 класс.Скачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Стереометрия для ЕГЭ: 2 - параллельные и скрещивающиеся прямыеСкачать