Расположение векторов скоростей точек механизма построенных из одного полюса

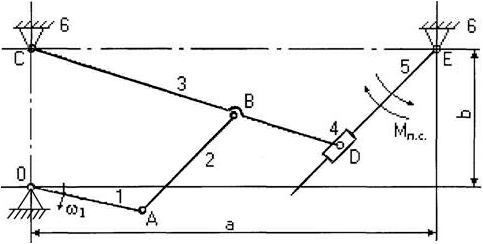
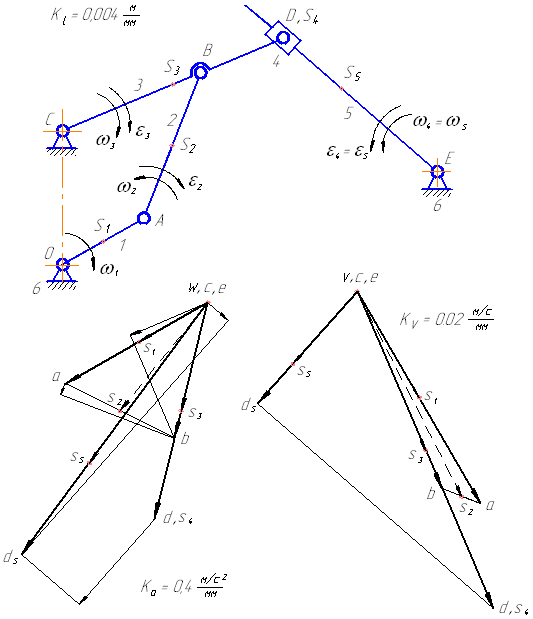
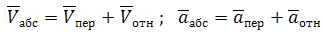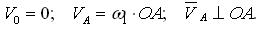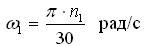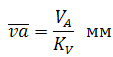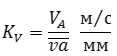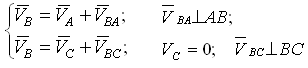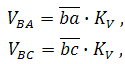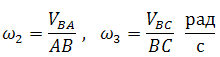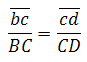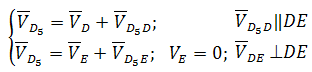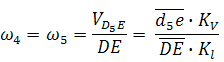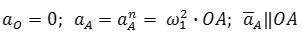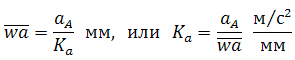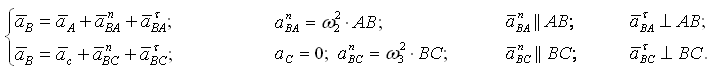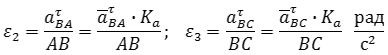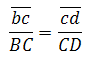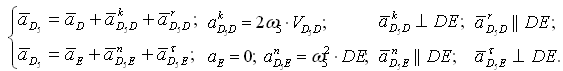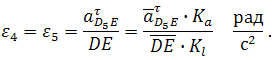Рассмотрим порядок построения планов скоростей и ускорений точек звеньев на примере кинематического исследования плоского рычажного механизма (рисунок 1).

Планом скоростей (ускорений) механизма называют чертеж, на котором скорости (ускорения) различных точек изображены в виде векторов, показывающих направления и величины (в масштабе) этих скоростей (ускорений) в данный момент времени.

Абсолютное движение любой точки звена может быть составлено из переносного и относительного. За переносное принимается известное движение какой-либо точки. Относительное – движение данной точки относительно той, движение которой принято за переносное:

На плане абсолютные скорости (ускорения) изображаются векторами, выходящими из полюса плана.

На конце вектора абсолютной скорости (ускорения) ставится строчная (маленькая) буква, соответствующая той точке механизма, скорость (ускорение) которой данный вектор изображает. Отрезок, соединяющий концы векторов абсолютных скоростей, представляет собой вектор относительной скорости соответствующих точек.

Рисунок 1 – Кинематическая схема плоского рычажного механизма

Рассмотрим построение планов для механизма, представленного на рисунке 1. Вначале рассматривается начальный механизм, а далее решение ведется по группам Ассура в порядке их присоединения.

По вычисленному значению V_A выбираем масштаб плана скоростей K_V и из произвольного полюса откладываем отрезок va изображающий эту скорость:

Можно также назначать отрезок va а масштаб K_V вычислять:

Истинные значения (в м/с) относительных скоростей V_BA и V_BC определяются после построения плана умножением соответствующих отрезков (в мм) на масштаб плана:

а зная их, можно определить и угловые скорости звеньев 2 и 3:

Скорость точки D на плане скоростей можно определить по подобию. (Если известны скорости двух точек одного и того же звена, то скорость любой третьей точки этого же звена можно определить, построив на плане скоростей фигуру, подобную фигуре, образованной этими же буквами на звене механизма). Точки С, В , D на звене 3 лежат на одной прямой. На плане строим отрезок сd, соблюдая условие подобия:

Группа Ассура второго класса 3-го вида (звенья 4,5) :

где D₅ — точка, находящаяся на звене 5 под точкой D. После определения скорости движения точки D₅ относительно точки E можно вычислить угловую скорость звеньев 4 и 5 ( ω₄=ω₅ , т. к. эти звенья соединяются поступательной парой):

Примечание: в данном случае размер DE является величиной переменной (т.е. в задании он отсутствует), поэтому в каждом положении механизма он определяется через отрезок на чертеже и масштаб длин.

План ускорений строится в таком же порядке.

Видео:Построение плана скоростей. ТММСкачать

Начальный механизм

Ускорение точки A состоит только из нормальной составляющей, т.к. задана постоянная угловая скорость первого звена ( ω₁=соnst ):

По вычисленному значению ускорения точки A выбирается масштаб плана ускорений и определяется отрезок на плане, соответствующий этому ускорению (или вычисляется масштаб плана ускорений по выбранному отрезку, изображающему ускорение точки A):

Здесь точка w – полюс плана ускорений.

Группа Ассура (звенья 2,3) второго класса 1-го вида:

После построения определяются a τ _BA и a τ _BC , по которым можно вычислить угловые ускорения звеньев 2 и 3:

Ускорение точки D определяем по подобию так же, как определяли скорость этой точки:

Рисунок 5 – Планы скоростей и ускорений для заданного положения механизма

Группа Ассура (звенья 4,5) второго класса 3-го вида:

Для определения направления a k _D5D надо вектор V_D5D повернуть на 90° в направлении ω₅ . Угловые ускорения:

При силовом расчете необходимо иметь ускорения центров масс ( a_si ), которые на плане ускорений определяются методом подобия.

Планы скоростей и ускорений для первого положения заданного механизма приведены на рисунке 5.

Уравнение планов скоростей и ускорений для каждой группы Ассура приведены в таблице 1.

Таблица 1 – Кинематический анализ групп Ассура II класса методом планов

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

План скоростей

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

План скоростей

• ПЛАН СКОРОСТЕЙ Скорости отдельных точек механизма в разных его положениях можно определять путем построения планов скоростей для соответ­ствующих положений. Этот метод определения скоростей состоит в следующем. Предположим, что известны по величине и направлению абсолют­ные скорости точек В и D твердого тела, совершающего плоско­ Фиг. 43. параллельное движение (фиг. 43, а), и пусть требуется определить величину и направление абсолютной

скорости точки М этого тела. Условимся в дальнейшем: 1) абсолютные скорости обозначать строчной латинской буквой v, отмечая прописной буквой в индексе точку, скорость которой обозначается: например vB — абсолютная скорость точки В; 2) относительные скорости обозначать также строчной латинской буквой v с индексом из двух букв, первой из кото­рых отмечать точку, скорость которой обозначается, а второй —точку, относительно

которой скорость рассматривается: например, vB D — скорость точки В относительно Людмила Фирмаль

точки О, vBD — скорость точки D относительно В; 3) чертой над буквой v отмечать, что скорость рас­сматривается как вектор, т. е. не только по величине, но и по направ­лению. Соединив прямой линией точки В и D; получаем схему тела в виде отрезка прямой BD. Так как при кинематическом исследовании гео­метрическая форма тела не имеет значения, а положение твердого тела, какой бы формы оно ни было, вполне определяется положением отрезка прямой линии на

нем, то в дальнейшем мы будем иметь в виду схему (фиг. 43, б) BD тела с точкой А4, расположенной на таких же расстояниях ВМ и DM от точек В и О, как и на фиг. 43, а. Изоб­ражая на фиг. 43, б тело в виде схемы ВО, будем точку М, лежащую вне линии ВО, считать точкой, принадлежащей телу ВО, т. е. жестко с ним связанной.30 Кинематический анализ плоских механизмов Отложим в выбранном масштабе от произвольной точки р (фиг. 43, в) векторы pb и pd абсолютных скоростей vB и vD. Соединив точки b и d прямой линией, получим план скоростей тела BD в виде треугольника pbd.

• На концах векторов pb и pd стрелки, указываю­щие направления абсолютных скоростей, являются лишними, так как направления векторов абсолютных скоростей, выходящих из точки р, понятны и без стрелок. Точка р называется полюсом плана скоростей. Вектор db (в на­правлении otJ k &) является вектором vBD; вектор bd (в направлении от b к d) является вектором vDB. Так как точка В относительно D (т. е. при условно неподвижной точке D) и точка D относительно В могут двигаться только по окруж­ностям с радиусами BD, то скорости vBD и vDB могут быть направлены только перпендикулярно к BD. Поэтому сторона bd треуголь­ника pbd

перпендикулярна к BD. На схеме тела прописными буквами В и D отмечены положения точек, абсолютные скорости которых заданы; на плане скоростей соответствующими строчными буквами b и d отмечены концы векто­ров абсолютных и относительных скоростей этих точек. Полюс р плана является начальной точкой векторов абсолютных скоростей всех точек тела BD. Точка тела BD, абсолютная скорость которой равна нулю, является мгновенным центром вращения тела BD. На плане скоростей точка,

изображающая абсолютную скорость мгновенного центра вращения, совпадает с Людмила Фирмаль

полюсом р. Скорости vB и vD направлены перпендикулярно к радиусам вра­щения точек В и D вокруг мгновенного центра, поэтому мгновен­ный центр Р вращения получается в точке пересечения перпенди­куляров к векторам скоростей vB и vD, проведенных из точек В и D. Треугольник PBD получается подобным треугольнику pbd и сход­ственно с ним расположен. Подобие треугольников вытекает из взаим­ной перпендикулярности сторон (например, сторона PD перпенди­кулярна к стороне pd). Сходственность расположения состоит в том, что при обходе вершин углов обоих треугольников в одном и том же направлении вершины, обозначенные одинаковыми буквами, обхо­дятся в одинаковой последовательности (например, при обходе поча­совой стрелке последовательно обходятся вершины PDBP

и pdbp). Перейдем теперь к определению скорости vM. Для определения этой скорости необходимо найти на плане скоростей точку m — конец вектора абсолютной скорости точки М. Точка М движется вместе с точкой В и, следовательно, со ско­ростью vB этой точки и, кроме того, движется относительно этой точки со скоростью vMB. Поэтому абсолютная скорость vM является геометрической суммой скоростей vB и vMB, что выражается следую­щим векторным уравнением: _ V M

V B + V MB-План скоростей 31 Правая часть этого уравнения говорит о том, что для получения вектора скорости им , являющейся геометрической суммой vB и vMB, надо провести вектор скорости vBi к концу этого вектора пристроить вектор скорости vMB и затем начало первого вектора соединить с концом второго. _ Вектор

скорости vB нами уже проведен — это вектор pb плана скоростей. Остается лишь к концу этого вектора, т. е. к точке Ь, пристроить вектор скорости vMB. Относительно точки В точка М может только вращаться; следовательно, вектор скорости vMB от точки b должен быть направлен перпендикулярно к линии ВМ. Для получения точки ш на плане надо определить длину вектора bm, а для этого надо знать величину скорости vMB, которая пока неиз­вестна. Поэтому от точки b мы проводим не вектор bm, а лишь линию действия этого вектора. Как видим, одного уравнения недостаточно, чтобы определить скорость точки М. Для определения им мы можем написать также

второе векторное уравнение: . = VD + vMD. Приняв во внимание, что вектор скорости vD — вектор pb — нами уже проведен и что скорость vMD может быть направлена только перпендикулярно к MD, проводим из точки d линию действия vMD перпендикулярно к MD. Точка т, в которой сходятся концы векторов абсолютной и относительных скоростей точки М, должна лежать на обеих линиях действия и потому находится в точке их пересече­ния. Соединив точку m с полюсом р, получаем вектор pm абсолютной скорости vM. Для нахождения точки m на плане скоростей мы соединили на схеме точку М с точками В и D, получив треугольник BMD, и на векторе bd относительных скоростей построили треугольник bmd, подобный

треугольнику BMD и сходственно с ним расположен­ный. Подобным же образом надлежит поступать при определении абсолютной и относительных скоростей любой точки тела BD. Тре­угольник bmd на плане скоростей получается в том случае, когда точка М на схеме лежит вне линии BD. Если точка М находится на отрезке BD или его продолжении, то на плане скоростей точки m расположится на отрезке bd или его продолжении. И в этом случае отрезки bm и dm будут пропорциональны отрезкам BM и DM. Если бы была задана скорость vM и требовалось найти на схеме такую принадлежащую телу точку Л4, которая в изображенном на фиг. 43 положении тела

движется с такой скоростью, то для этого надо было бы провести на плане вектор pm, построить треуголь-32 Кинематический анализ плоских механизмов ник bmd, а затем построить на схеме треугольник BMD, подобный треугольнику bmd и сходственно с ним расположенный. Масштаб плана скоростей выявляется при проведении первого вектора: где — масштаб плана скоростей в м/сек-мм; vB — величина абсолютной скорости точки В в м/сек; pb — длина вектора абсолютной скорости точки В в мм. Для определения величины скорости какой-либо точки по плану скоростей длину вектора этой скорости надлежит умножить на масштаб плана.

Угловая скорость со вращения тела BD может быть получена путем деления абсолютной скорости какой-либо точки тела на ее рас­стояние до мгновенного центра вращения; например где vB — в м/сек и РВ — в м. Если точка Р находится вне чертежа, то на основании подобия треугольников PBD и pbd вместо РВ можно подставить k-pb, где k — отношение длин сходственных сторон, равное k = Поступив таким образом, получаем (выражая pb в мм и умножая vB на 103 мм/м) (О = 103 -uB : k-pb = Выше при построении плана скоростей мы располагали четырьмя данными: величинами и направлениями обеих скоростей vB и vD. План скоростей может быть построен и по

трем любым из этих дан­ных. Например, если бы скорость vD была известна только по направ­лению, то из полюса р вместо вектора pd мы смогли бы провести лишь линию действия этого вектора; положение точки d определилось бы в этом случае в результате проведения линии действия vDB — вто­рого геометрического слагаемого векторного уравнения vD = vB + + VDBПример 1. Для механизма I класса 1-го порядка в изображенном нафиг. 44, а положении построить план скоростей и, пользуясь планом, определить считая точки М и N принадлежащими звену АВ. Скорость точки В задана вектором vB . Из полюса р проводим pb — вектор vB (фиг. 44, б). Так как точка А неподвижна, то точка а — конец вектора ра скорости од совпадает с полюсом р. Линия pb является планом

скоростей. Для определения им строим на линии pb треугольник ptnb, подобный треуголь­нику АМВ и сходственно с этим треугольником расположенный; pm — векторПлан скоростей Подобным же образом получаем на плане рп — вектор v^. Соединив прямой линией точки т и п , получаем run — вектор vmN . Пример 2. Звенья ВС и CD соединены в точкеС во вращательную_пару (фиг. 45, а). Скорости точек В и D заданы векторами св и vp. Определить VQ. Точка С, являясь частью звена ВС, движется сточкой В и, следовательно, со ско­ростью vB кроме этого, она движется и вокруг точки В со скоростью vqb-Являясь частью звена CD, точка С движется с точкой D и,

следовательно, со ско­ростью Up; кроме этого, она движется вокруг точки D со скоростью урр. В обоих случаях скорость vq получается в виде геометрической суммы двух сла­гаемых. Поэтому для определения vq располагаем двумя векторными уравнениями: VC — VB VCB’ VC = vd + VCDРуководствуясь первым из этих уравнений, мы должны провести на плане ско­ростей (фиг. 45± б) сначала вектор pb скорости ив, а затем к точке b пристроить век­тор скорости VQBСкорость vqb может быть направлена только перпендикулярно к ВС, так как точка С относительно точки В может двигаться только по окружности с радиусом ВС. Так как величина vcb неизвестна, то от точки b проводим лишь линию действия vcb перпендикулярно к ВС. В соответствии со вторым уравнением и

руководствуясь только что изложенными соображениями, проводим pd — вектор vD — и от точки d линию действия vcp пер­пендикулярно к CD. Так как точка с плана скоростей должна находиться на обеих линиях действия, то, соединив точку пересечения их с полюсом, получаем рс — вектор vp. Пример 3. На фиг. 46, а приведена схема четырехзвенного механизма с тремя вращательными и одной поступательной парой. Ведущее звено 1 связано с ползуном 2 в поступательную пару; звено 3 связано с ползуном во вращательную пару В. Угловая скорость звена 1 направлена по часовой стрелке,

величина ее известна. Определить ^ Отметим на звене 1 точку Вх , расположенную под точкой В, т. е. находящуюся в расстоянии АВХ от точки А, равном АВ. 3 Зиновьев 61234 Кинематический анализ плоских механизмов Для определения vB можем написать два векторных уравнения: V B = vbx + v bbx V B = VC + VB C . В соответствии с первым уравнением мы должны провести pbx — вектор Б# и к концу этого вектора пристроить вектор bx b скорости °в х 1авх —

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Видео:#Построение плана скоростей кулисного механизма-практика (КП)Скачать

Определение скоростей и ускорений

Планом скоростей (ускорений) механизма называется пучок векторов, выходящих из одной точки (полюса плана), каждый из которых в некотором масштабе изображает вектор абсолютной скорости (абсолютного ускорения) какой-либо точки механизма, а отрезки, соединяющие их концы, изображают векторы относительных скоростей (относительных ускорений).

Построение плана скоростей сводится к реализации известного положения теоретической механики, согласно которому при плоско-параллельном движении твёрдого тела (звена) скорость любой его точки равна векторной сумме скорости в поступательном переносном движении вместе с другой точкой, принятой в качестве полюса, и скорости её в относительном вращательном движении относительно этого полюса.

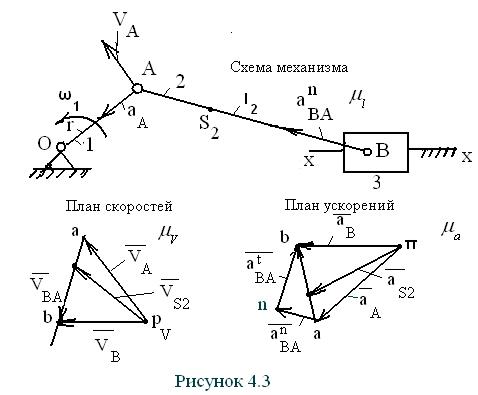
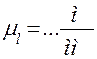
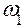
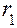
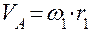
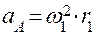
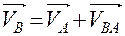
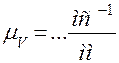
Рассмотрим построение планов скоростей и ускорений на примере кривошипно-ползунного механизма (рис. 4.3). Схема механизма должна быть изображена в масштабе в исследуемом положении. Прежде необходимо определить параметры движения точки А. Её скорость по величине равна произведению угловой скорости кривошипа 1 на его радиус , т. е. и направлена перпендикулярно кривошипу в сторону движения точки А. Ускорение точки А по величине равно произведению квадрата угловой скорости кривошипа также на его радиус, т. е. и направлено от точки А к точке О, так как совпадает с нормальной составляющей полного ускорения точки А из-за равенства нулю тангенциальной составляющей ускорения (угловое ускорение кривошипа принимается равным нулю). Точка А принадлежит не только кривошипу, но и шатуну 2 и принимается в качестве полюса относительного вращения точки В. Скорость точки В определяется векторным равенством , т. е. скорость точки В равна скорости точки А плюс скорость точки В относительно точки А. В этом равенстве первое слагаемое правой части известно по величине и по направлению, второе слагаемое направлено перпендикулярно шатуну 2 в данном положении, т. е. известно по направлению, и, наконец, вектор левой части направлен параллельно направляющим ползуна. При этих условиях треугольник скоростей легко строится в предварительно выбранном масштабе .

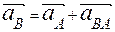
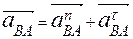
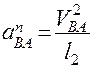
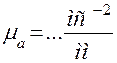
Построение плана ускорений производится в той же последовательности, что и план скоростей. При этом используется векторное равенство , в котором первый вектор правой части известен полностью, второй неизвестен ни по величине, ни по направлению. Вектор левой части известен по направлению – он направлен параллельно направляющим ползуна. В этих условиях треугольник ускорений не строится. Разложим вектор относительного ускорения на две составляющих, согласно равенству . Первое слагаемое представляет собой относительное нормальное ускорение, направленное от точки В к точке А и равное по величине частному от деления квадрата относительной скорости на длину шатуна, т. е. . Второе слагаемое, относительное тангенциальное ускорение направлено перпендикулярно шатуну 2 и неизвестно по величине. Теперь план ускорений строится без затруднений с применением заранее выбранного масштаба . Планы скоростей и ускорений данного механизма представлены на рис. 4.3.

Используя планы, легко найти физические величины скоростей и ускорений, для этого необходимо измерить отрезки в миллиметрах, выражающие скорости и ускорения, и умножить их на соответствующий масштаб.

Абсолютная скорость точки В: , .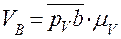

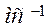
Относительная скорость точки В: , .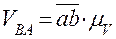

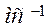
Угловая скорость шатуна 2: , .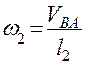

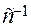
Тангенциальное ускорения точки В относительно точки А:

, .

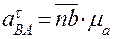
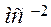
Полное относительное ускорение: , .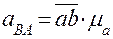

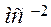
Угловое ускорение шатуна 2: , .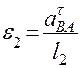

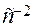
4.4. Метод кинематических диаграмм

(метод графического дифференцирования)

Основой метода служит известное положение математики, согласно которому производная функции, заданной в виде графика, в какой-либо её точке численно равна тангенсу угла наклона касательной, проведённой в этой точке к графику функции, то есть

.

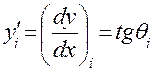
Так как теория механизмов и машин имеет дело с именованными числами, то при определении величины тангенса необходимо учитывать масштабы по осям координат графика функции (рис. 4.4), тогда

.

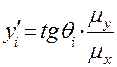
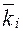
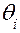
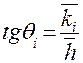
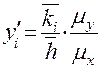
Выберем горизонтальный отрезок произвольной длины и проведём из его левого конца наклонную прямую, параллельную касательной, а из правого конца – вертикальную прямую до пересечения с наклонной. Вычислим длину отрезка, полученного на вертикали и обозначенного на рис. 4.4 буквой . Построенный треугольник является прямоугольным с углом против вертикального катета, равным . Поэтому, записав из треугольника и подставив это отношение в предыдущее выражение, получаем

.

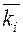
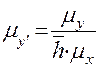
В правой части этого выражения переменной величиной является только , остальные образуют постоянное число, которое можно считать масштабом, то есть

.

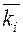
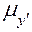
Таким образом мы убедились, что отрезок в масштабе выражает производную в данной точке графика.

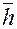
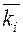
Для применения рассмотренной методики необходимо предварительно построить график или функции положения механизма, или график аналога скорости. Чтобы построить график производной, необходимо на продолжении оси абсцисс этого графика в левую сторону от оси ординат выбрать произвольный отрезок и на нём строить все треугольники, необходимые для определения отрезков . Все эти отрезки получаются на оси ординат, но каждый из них необходимо разместить на ординатной прямой соответствующего номера, а их концы соединить плавной кривой. Эта процедура даст искомый график.

Вопросы для самопроверки

1. Сформулируйте задачи кинематического анализа механизмов с низшими парами.

2. Перечислите методы исследования кинематики механизмов.

3. Что должно быть задано для исследования кинематики механизма?

4. В чём заключается сущность аналитического метода исследования кинематики?

5. Что называется масштабом в ТММ?

6. Что такое разметка механизма?

7. Для чего строится разметка?

8. Как определяются скорость и ускорение конца кривошипа?

9. Запишите векторные уравнения для построения планов скоростей и ускорений и объясните их составляющие. Какое правило механики положено в основу этих уравнений?

10. Как определяются скорости и ускорения центра масс шатуна?

11. Как определить угловые скорость и ускорение стержневого звена?

12. Какое правило математики положено в основу графического дифференцирования функции, заданной в виде графика?

13. Приведите пример построении графика производной при заданном графике функции.

14. Как определяются масштабы по осям координат при построении графика производной?

📸 Видео

Кинематика механизма. Два способа решенияСкачать

Занятие 2 - Построение планов скоростейСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Скорости и ускорения точек механизмаСкачать

Координаты вектора в пространстве. 11 класс.Скачать

Угол между векторами | МатематикаСкачать

№805. Три точки А, В и С расположены так, что ВС = ½ АВ. Докажите, что для любой точки О справедливоСкачать

03 Построение плана скоростей механизмаСкачать

Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать

Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

План скоростей шарнирного трехзвенного механизмаСкачать

План ускорений кривошипно-ползунного механизмаСкачать

Урок 9. Проекции вектора на координатные осиСкачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Координаты вектора. 9 класс.Скачать

Кинематический расчет плоского механизма Задание К3Скачать