Два вектора в круглых скобках через запятую (6 видео)

Какие произведения векторов Вы знаете?

Содержание

Primary tabs
Forums:
1) Скалярное произведение векторов
2) Векторное произведение векторов
Знакомимся с вектором
Линейная алгебра
Что такое вектор
Как записывать
Скаляр
Как изображать
И зачем нам это всё
Что дальше
Вектор. Векторное произведение векторов.
🌟 Видео

Видео:Полный разбор задач с векторами №2 ЕГЭ ПРОФИЛЬ 2024 | Профильная математика ЕГЭ 2024 | УМСКУЛСкачать

Primary tabs

Forums:

В математике определены два базовых типа произведения векторов, это =

Видео:Как искать скалярное произведение векторов? В ЕГЭ ПРОФИЛЬ НОВАЯ ЗАДАЧА!Скачать

1) Скалярное произведение векторов

Скалярное произведение векторов A и B определяется как число, равное произведению модулей этих векторов на косинус угла между ними.

Т.е. скалярное произведение векторов а и b равно числу с, которое определяется по формуле =

где ф — угол между векторами а и b.

Скалярное произведение обозначается=

символом обычного умножения — точки (в txt вместо неё звёздочка)
(A*B)
A*B

или просто — без скобок —

AxB

Видео:Профильный ЕГЭ 2024. Векторы. Координатная плоскость. Задача 2Скачать

2) Векторное произведение векторов

Векторным произведением векторов A и B называется вектор , равный по величине произведению модулей векторов на синус угла между ними и направленный перпендикулярно плоскости вектором сомножителей в ту сторону , откуда поворот от первого сомножителя А ко второму сомножителю В на меньший угол виден против хода часовой стрелки.

Векторным произведением вектора a на вектор b в пространстве трёхмерном называется вектор c, удовлетворяющий следующим требованиям:

где ф — угол между векторами а и b.

Векторное произведение обозначается:

[AxB]
[A,B]
или просто — без скобок —
AxB

то есть вектора в квадратных скобках могут просто разделяться запятой

Видео:Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать

Знакомимся с вектором

Основы линейной алгебры для тех, кого это миновало в универе.

Вы наверняка слышали много историй о программистах, которые учились в технических вузах, изучали высшую математику и теперь пользуются этими знаниями в программировании. И если кого-то это не коснулось, может быть ощущение, что он пропустил в жизни что-то важное.

Будем это исправлять. Попробуем разобрать некоторые базовые понятия из математики за пределами школьной программы. И заодно покажем, как оно связано с программированием и для каких задач полезно.

⚠️ Математики, помогайте. Мы тут многое упростили, поэтому будем рады увидеть ваши уточнения и замечания в комментариях.

Видео:Новое задание профиля №2. Все, что нужно знать о векторах | Аня МатеманяСкачать

Линейная алгебра

Есть математика: она изучает абстрактные объекты и их взаимосвязи. Благодаря математике мы знаем, что если сложить два объекта с ещё двумя такими же объектами, то получится четыре объекта. И неважно, что это были за объекты: яблоки, козы или ракеты. Математика берёт наш вещественный мир и изучает его более абстрактные свойства.

Внутри математики есть алгебра: если совсем примитивно, то в алгебре мы вместо чисел начинаем подставлять буквы и изучать ещё более абстрактные свойства объектов.

Например, мы знаем, что если a + b = c , то a = c − b . Мы не знаем, что стоит на местах a, b или c, но для нас это такой абстрактный закон, который подтверждается практикой.

Внутри алгебры есть линейная алгебра — она изучает векторы, векторные пространства и другие абстрактные понятия, которые в целом относятся к некой упорядоченной информации. Например, координаты ракеты в космосе, биржевые котировки, расположение пикселей в изображении — всё это примеры упорядоченной информации, которую можно описывать векторами. И вот их изучает линейная алгебра.

В программировании линейная алгебра нужна в дата-сайенс, где из упорядоченной информации создаются алгоритмы машинного обучения.

Если представить линейную алгебру в виде дома, то вектор — это кирпич, из которого всё состоит. Сегодня разберёмся, что такое вектор и как его понимать.

Видео:Координаты вектора в пространстве. 11 класс.Скачать

Что такое вектор

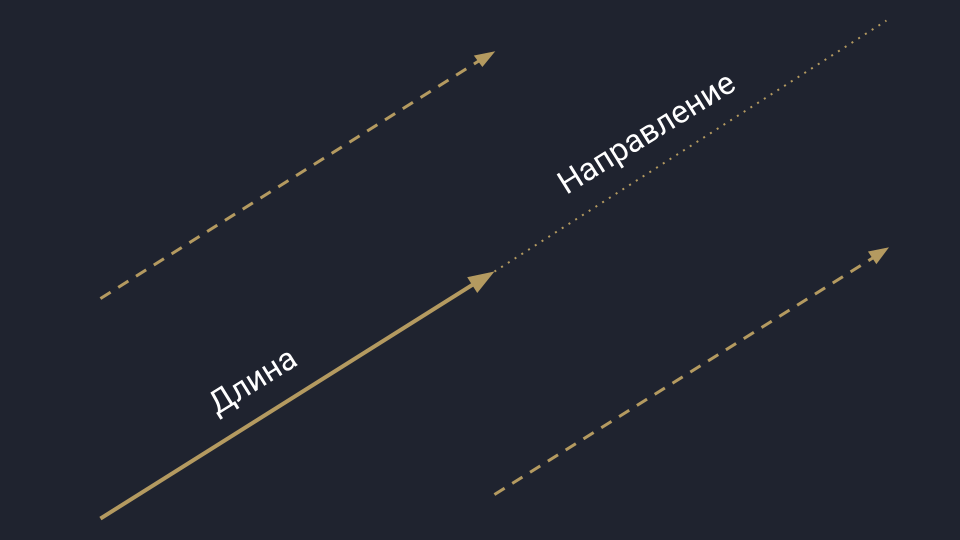
Вы наверняка помните вектор из школьной программы — это такая стрелочка. Она направлена в пространство и измеряется двумя параметрами: длиной и направлением. Пока длина и направление не меняются, вектор может перемещаться в пространстве.

Физическое представление вектора: есть длина, направление и нет начальной точки отсчёта. Такой вектор можно как угодно двигать в пространстве

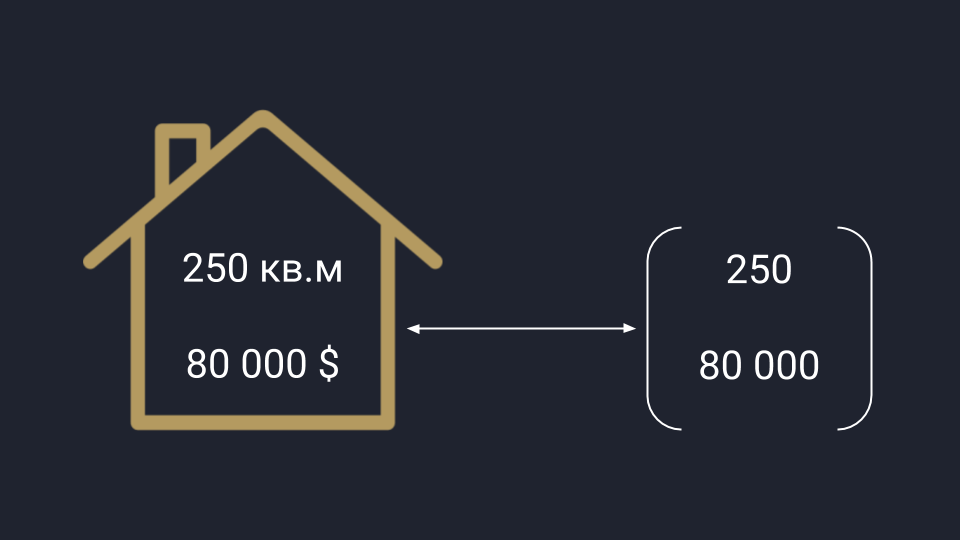
У аналитиков вектор представляется в виде упорядоченного списка чисел: это может быть любая информация, которую можно измерить и последовательно записать. Для примера возьмём рынок недвижимости, который нужно проанализировать по площади и цене домов — получаем вектор, где первая цифра отвечает за площадь, а вторая — за цену. Аналогично можно сортировать любые данные.

Аналитическое представление вектора: данные можно перевести в числа

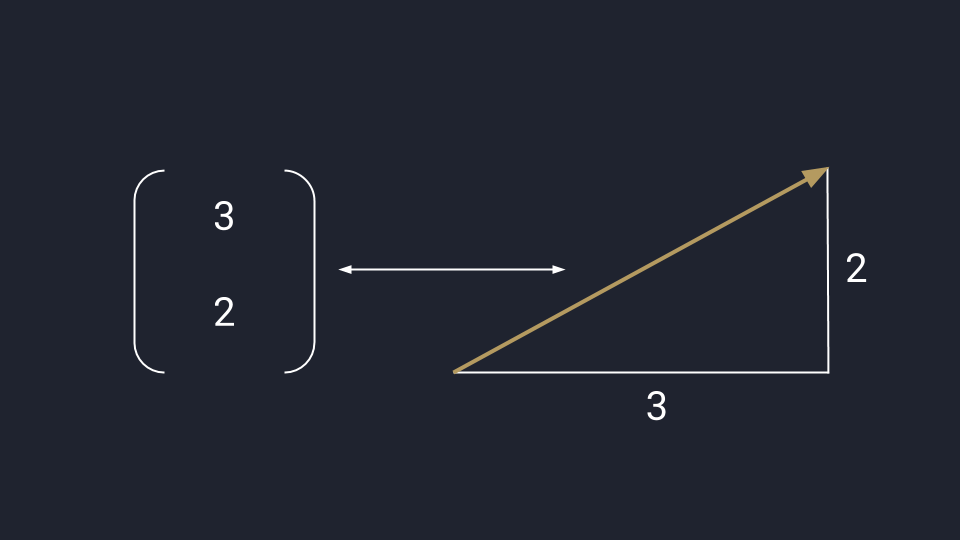
Математики обобщают оба подхода и считают вектор одновременно стрелкой и числом — это связанные понятия, перетекающие друг в друга в зависимости от задачи. В одних случаях удобней считать, а в других — показать всё графически. В обоих случаях перед нами вектор.

Математическое представление вектора: данные можно перевести в числа или график

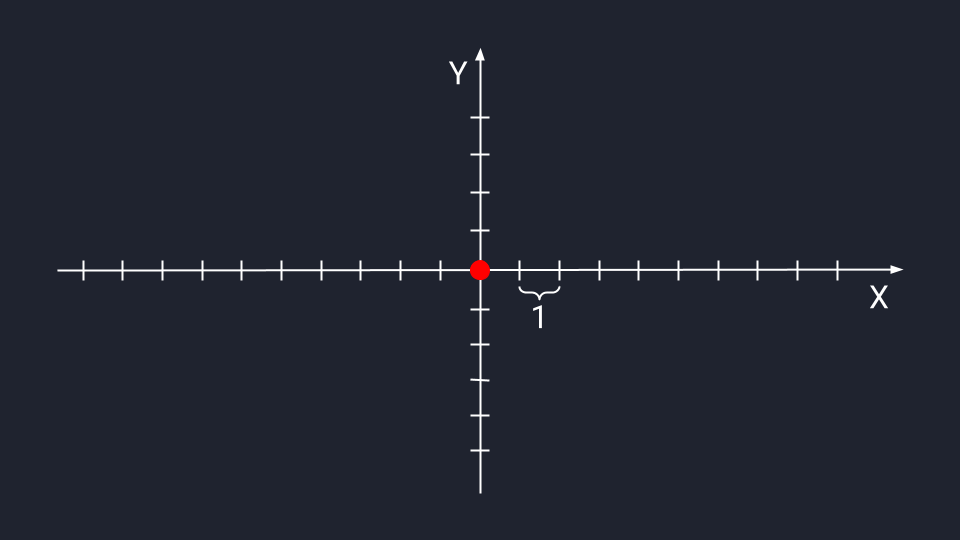
В дата-сайенс используется математическое представление вектора — программист может обработать данные и визуализировать результат. В отличие от физического представления, стрелки векторов в математике привязаны к системе координат Х и У — они не блуждают в пространстве, а исходят из нулевой точки.

Векторная система координат с базовыми осями Х и Y. Место их пересечения — начало координат и корень любого вектора. Засечки на осях — это отрезки одной длины, которые мы будем использовать для определения векторных координат

👉 Получается, вектор – это такой способ записывать, хранить и обрабатывать не одно число, а какое-то организованное множество чисел. Благодаря векторам мы можем представить это множество как единый объект и изучать его взаимодействие с другими объектами.

Например, можно взять много векторов с ценами на недвижимость, как-то их проанализировать, усреднить и обучить на них алгоритм. Без векторов это были бы просто «рассыпанные» данные, а с векторами — порядок.

Видео:2. Векторы в параллелограмме Решение задач №2Скачать

Как записывать

Вектор можно записать в строку или в столбец. Для строчной записи вектор обозначают одной буквой, ставят над ней черту, открывают круглые скобки и через запятую записывают координаты вектора. Для записи в столбец координаты вектора нужно взять в круглые или квадратные скобки — допустим любой вариант.

Строгий порядок записи делает так, что каждый набор чисел создаёт только один вектор, а каждый вектор ассоциируется только с одним набором чисел. Это значит, что если у нас есть координаты вектора, то мы их не сможем перепутать.

Способы записи вектора

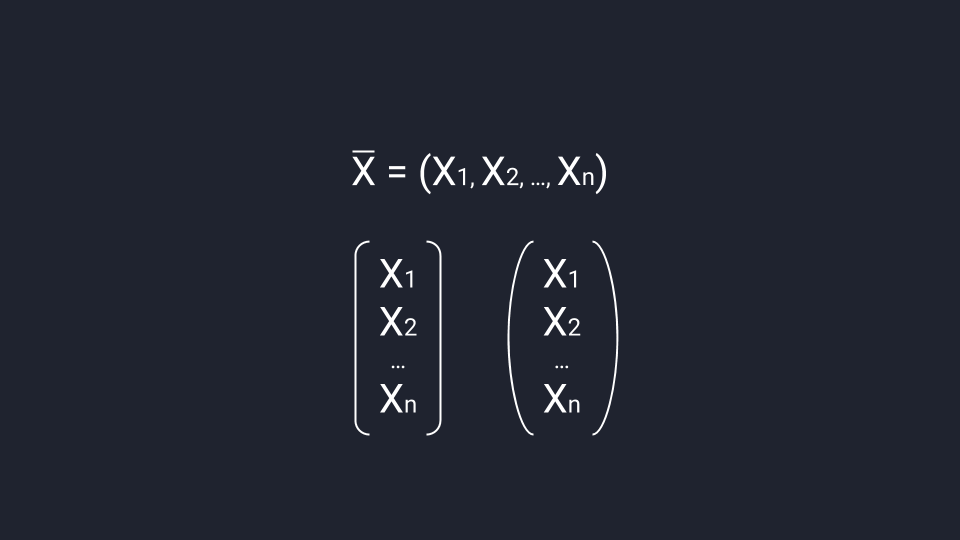
Скаляр

Помимо понятия вектора есть понятие скаляра. Скаляр — это просто одно число. Можно сказать, что скаляр — это вектор, который состоит из одной координаты.

Помните физику? Есть скалярные величины и есть векторные. Скалярные как бы описывают просто состояние, например, температуру. Векторные величины ещё и описывают направление.

Видео:18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Как изображать

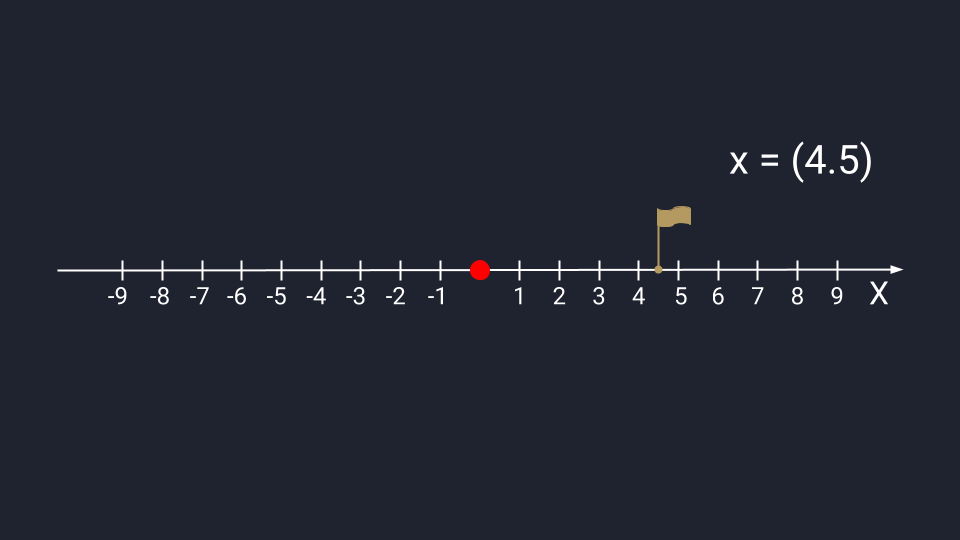
Вектор из одного числа (скаляр) отображается в виде точки на числовой прямой.

Графическое представление скаляра. Записывается в круглых скобках

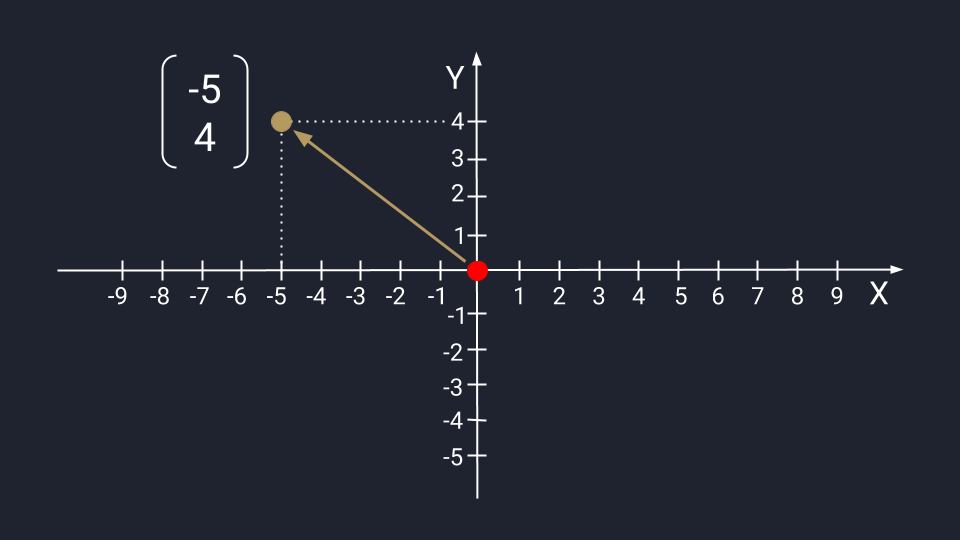
Вектор из двух чисел отображается в виде точки на плоскости осей Х и Y. Числа задают координаты вектора в пространстве — это такая инструкция, по которой нужно перемещаться от хвоста к стрелке вектора. Первое число показывает расстояние, которое нужно пройти вдоль оси Х; второе — расстояние по оси Y. Положительные числа на оси Х обозначают движение вправо; отрицательные — влево. Положительные числа на оси Y — идём вверх; отрицательные — вниз.

Представим вектор с числами −5 и 4. Для поиска нужной точки нам необходимо пройти влево пять шагов по оси Х, а затем подняться на четыре этажа по оси Y.

Графическое представление числового вектора в двух измерениях

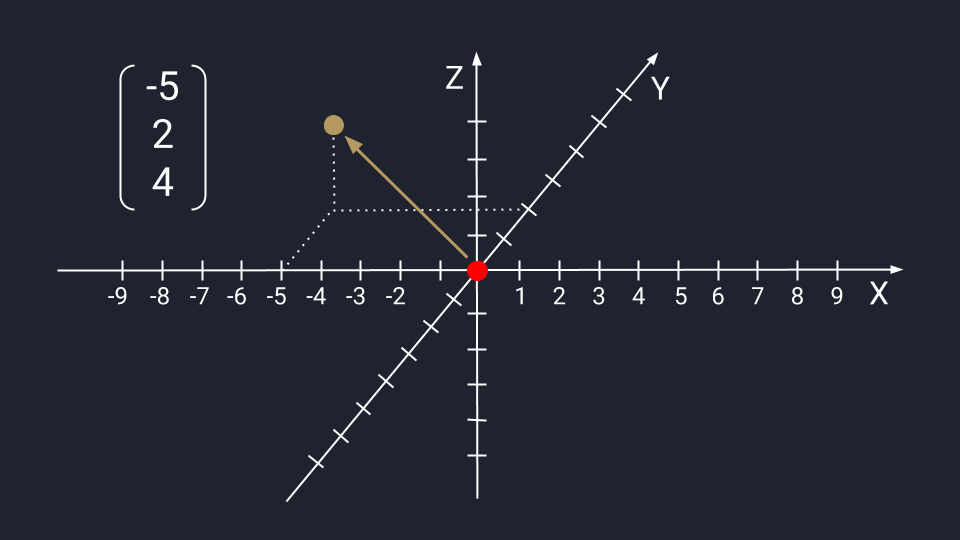
Вектор из трёх чисел отображается в виде точки на плоскости осей Х, Y и Z. Ось Z проводится перпендикулярно осям Х и У — это трёхмерное измерение, где вектор с упорядоченным триплетом чисел: первые два числа указывают на движение по осям Х и У, третье — куда нужно двигаться вдоль оси Z. Каждый триплет создаёт уникальный вектор в пространстве, а у каждого вектора есть только один триплет.

Если вектор состоит из четырёх и более чисел, то в теории он строится по похожему принципу: вы берёте координаты, строите N-мерное пространство и находите нужную точку. Это сложно представить и для обучения не понадобится.

Графическое представление числового вектора в трёх измерениях. Для примера мы взяли координаты −5, 2, 4

Помните, что все эти записи и изображения с точки зрения алгебры не имеют отношения к нашему реальному трёхмерному пространству. Вектор — это просто какое-то количество абстрактных чисел, собранных в строгом порядке. Вектору неважно, сколько там чисел и как их изображают люди. Мы же их изображаем просто для наглядности и удобства.

Например, в векторе спокойно может быть 99 координат. Для его изображения нам понадобилось бы 99 измерений, что очень проблематично на бумаге. Но с точки зрения вектора это не проблема: перемножать и складывать векторы из двух координат можно так же, как и векторы из 9999999 координат, принципы те же.

Видео:Линейная алгебра. Векторы и операции над векторами.Скачать

И зачем нам это всё

Вектор — это «кирпичик», из которого строится дата-сайенс и машинное обучение. Например:

На основании векторов получаются матрицы. Если вектор — это как бы линия, то матрица — это как бы плоскость или таблица.
Машинное обучение в своей основе — это перемножение матриц. У тебя есть матрица с данными, которые машина знает сейчас; и тебе нужно эту матрицу «дообучить». Ты умножаешь существующую матрицу на какую-то другую матрицу и получаешь новую матрицу. Делаешь так много раз по определённым законам, и у тебя обученная модель, которую на бытовом языке называют искусственным интеллектом.

Кроме того, векторы используются в компьютерной графике, работе со звуком, инженерном и просто любом вычислительном софте.

И давайте помнить, что вектор — это не какая-то сложная абстрактная штука, а просто сумка, в которой лежат числа в определённом порядке. То, что мы называем это вектором, — просто нюанс терминологии.

Видео:ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать

Что дальше

В следующий раз разберём операции с векторами. Пока мы готовим материал — рекомендуем почитать интервью с Анастасией Никулиной. Анастасия ведёт ютуб-канал по дата-сайнс и работает сеньором дата-сайентистом в Росбанке.

Видео:Скалярное произведение векторов. 9 класс.Скачать

Вектор. Векторное произведение векторов.

Векторное произведение — это псевдовектор, который перпендикулярен плоскости, построенной по двум

сомножителям, которые являются результатом бинарной операции «векторное умножение» над

векторами в трёхмерном евклидовом пространстве.

Векторное произведение не имеет свойств коммутативности и ассоциативности (антикоммутативное)

Векторное произведение помогает в «измерении» перпендикулярности векторов — модуль

векторного произведения двух векторов равен произведению модулей этих векторов, если они

перпендикулярны, и стремится к нулю, если векторы параллельны или антипараллельны.

В отличие от формулы для вычисления по координатам векторов скалярного произведения в

трёхмерной прямоугольной системе координат, формула для векторного произведения зависит

от ориентации прямоугольной системы координат или, говоря другими словами, её «хиральности».

Векторное произведение двух векторов обозначается квадратными скобками:

Свойства векторного произведения векторов.

1. Геометрический смысл векторного произведения векторов.

Векторным произведением вектора на вектор является

вектор , длина его численно соответствует площади

параллелограмма, который построен на векторах и ,

перпендикулярный к плоскости этих векторов и направлен

так, чтоб самое маленькое вращение от к около

вектора происходило против часовой стрелки, если взгляд вести

с конца вектора .

Модуль векторного произведения двух векторов и = площади параллелограмма, который

построен на них:

Площадь треугольника строящегося на векторах и соответствует одной второй модуля

векторного произведения векторов и :

2. Вектор перпендикулярен векторам и , то есть и ;

3. Вектор направлен таким образом, что поворот от вектора к вектору происходит против часовой стрелки, если смотришь с конца вектора (в таком случае тройка векторов , и – правая).