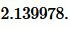С помощю этого онлайн калькулятора можно найти радиус описанной окружности около любого треугольника, в том числе радиус описанной окружности около прямоугольного треугольника. Для нахождения радиуса окружности описанной около треугольника введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
- 1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
- 2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
- 3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
- 4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
- Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 1) 25 см 2) 41 дм 3) 130мм 4) 61 см?
- Найдите радиусе вписанной и описанной окружностей прямоугольного треугольника если его катеты равны 5 и 12 см , гипотенуза равна 13 см?
- Гипотенуза прямоугольного треугольника равна 16, а радиус вписанной окружности этого треугольника равен 3?
- Радиус окружности, описанной около прямоугольного треугольника равна 5, 5 см?
- Найти радиус окружности описанной возле прямоугольного треугольника с гипотенузой 10 см?
- Прямоугольный треугольник вписан в окружность, его катеты равны 15 и 8?
- Гипотенуза прямоугольного треугольника равна а, радиус вписанной окружности равен b?
- Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 25см?
- Радиус окружности , описанной около прямоугольного треугольника , равен 5, а высота, опущенная на гипотенузу равна 3 см?
- В прямоугольном треугольнике гипотенуза равна 10 см?
- Один из катетов прямоугольного треугольника равно 4 см?
- Катеты прямоугольного треугольника 18 и 24?
- Радиус вписанной окружности в прямоугольный треугольник онлайн
- 1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
- 2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
- 3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

1. Радиус окружности описанной около прямоугольного треугольника, если известна гипотенуза треугольника
Пусть известна гипотенуза c прямоугольного треугольника (Рис.1). Найдем радиус описанной окружности около треугольника.
 |
На странице Радиус окружности описанной около треугольника формула радиуса описанной окружности около треугольника по стороне и противолежащему углу имеет вид:
| ( small R=frac ) |
где C − угол противолежащий гипотенузе прямоугольного треугольника. Поскольку угол, противолежащий гипотенузе − прямой, то получим:
| ( small R=frac=frac, ) |
| ( small R=frac. ) | (1) |
Пример 1. Известна гипотенуза ( small с=frac ) прямоугольного треугольника. Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около треугольника воспользуемся формулой (1).
Подставим значение ( small c=frac ) в (1):
 |
Ответ:
Видео:Задание 25 Прямоугольный треугольник Вписанная окружностьСкачать
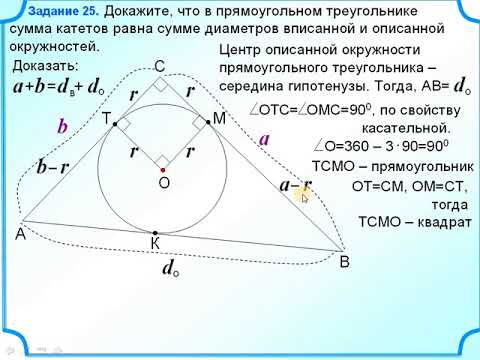
2. Радиус окружности описанной около прямоугольного треугольника, если известны катеты треугольника
Пусть известны катеты a и b прямоугольного треугольника. Найдем радиус описанной окружности около треугольника (Рис.2).
 |
Из теоремы Пифагора запишем формулу гипотенузы, выраженная через катеты:
| ( small c=sqrt. ) | (2) |
Подставляя (2) в (1), получим:
| ( small R=frac=frac<large sqrt>, ) |
| ( small R=frac<large sqrt>. ) | (3) |
Пример 2. Катеты прямоугольного треугольника равны: ( small a=15 , ; b=3.) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (3). Подставим значения ( small a=15 , ; b=3) в (3):
 |
Ответ:
Видео:ОГЭ Задание 25 Окружность вписанная в прямоугольный треугольникСкачать

3. Радиус окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника
 |
Формула для вычисления радиуса окружности описанной около прямоугольного треугольника, если известны катет и противолежащий угол треугольника аналогична формуле вычисления радиуса описанной окружности около произвольного треугольника (см. статью на странице Радиус описанной окружности около треугольника онлайн):
 | (4) |
Видео:Сможешь найти радиус окружности? Окружность, вписанная в прямоугольный треугольникСкачать

4. Радиус окружности описанной около прямоугольного треугольника, если известны катет и прилежащий острый угол треугольника
Пусть известны катет a и прилежащий острый угол B прямоугольного треугольника (Рис.4). Найдем радиус описанной окружности около треугольника.
 |
Так как треугольник прямоугольный, то сумма острых углов треугольника равна 90°:
| ( small angle A+angle B=90°. ) |
| ( small angle A=90°-angle B. ) | (5) |
Подставляя (5) в (4), получим:
| ( small R=frac=frac) ( small =frac ) |
| ( small R=frac. ) | (6) |
Пример 3. Катет прямоугольного треугольника равен: ( small a=15 ,) а прилежащий угол равен ( small angle B=25°. ) Найти радиус окружности описанной около треугольника.
Решение. Для нахождения радиуса окружности описанной около прямоугольного треугольника воспользуемся формулой (6). Подставим значения ( small a=15 , ; angle B=25° ) в (6):
 |
Ответ:
Видео:Радиус описанной окружностиСкачать

Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 1) 25 см 2) 41 дм 3) 130мм 4) 61 см?
Геометрия | 5 — 9 классы
Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 1) 25 см 2) 41 дм 3) 130мм 4) 61 см.
Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.
Видео:Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Найдите радиусе вписанной и описанной окружностей прямоугольного треугольника если его катеты равны 5 и 12 см , гипотенуза равна 13 см?
Найдите радиусе вписанной и описанной окружностей прямоугольного треугольника если его катеты равны 5 и 12 см , гипотенуза равна 13 см.
Видео:Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Гипотенуза прямоугольного треугольника равна 16, а радиус вписанной окружности этого треугольника равен 3?
Гипотенуза прямоугольного треугольника равна 16, а радиус вписанной окружности этого треугольника равен 3.
Найдите периметр треугольника.
Видео:Задание 25 Прямоугольный треугольник Вписанная описанная окружностиСкачать

Радиус окружности, описанной около прямоугольного треугольника равна 5, 5 см?
Радиус окружности, описанной около прямоугольного треугольника равна 5, 5 см.
Чему равна гипотенуза этого треугольника.
Видео:Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Найти радиус окружности описанной возле прямоугольного треугольника с гипотенузой 10 см?
Найти радиус окружности описанной возле прямоугольного треугольника с гипотенузой 10 см.
Видео:ЗАДАНИЕ 1| ЕГЭ ПРОФИЛЬ| Радиус окружности, описанной около прямоугольного треугольника, равен 4. НайСкачать

Прямоугольный треугольник вписан в окружность, его катеты равны 15 и 8?
Прямоугольный треугольник вписан в окружность, его катеты равны 15 и 8.
Гипотенуза проходит через центр окружности.
Найдите радиус окружности.
Видео:Радиус описанной окружностиСкачать

Гипотенуза прямоугольного треугольника равна а, радиус вписанной окружности равен b?
Гипотенуза прямоугольного треугольника равна а, радиус вписанной окружности равен b.
Найдите его периметр.
Видео:Задание 24 Радиус окружности вписанной в прямоугольный треугольникСкачать
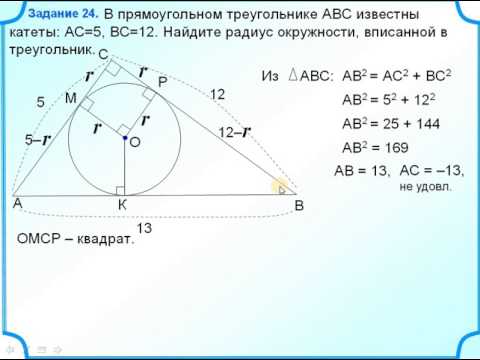
Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 25см?
Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 25см.
Видео:Прямоугольный треугольник Радиус описанной окружностиСкачать
Радиус окружности , описанной около прямоугольного треугольника , равен 5, а высота, опущенная на гипотенузу равна 3 см?
Радиус окружности , описанной около прямоугольного треугольника , равен 5, а высота, опущенная на гипотенузу равна 3 см.
Найдите площадь этого треугольника.
Видео:найти радиус окружности, описанной вокруг треугольникаСкачать

В прямоугольном треугольнике гипотенуза равна 10 см?
В прямоугольном треугольнике гипотенуза равна 10 см.
Найдите радиус окружности, описанной около этого треугольника.
Видео:№705. Около прямоугольного треугольника ABC с прямым углом С описана окружность. Найдите радиусСкачать

Один из катетов прямоугольного треугольника равно 4 см?
Один из катетов прямоугольного треугольника равно 4 см.
А проекция его на гипотенузу 4 / 3 см.
Найти радиус описанной окружности.
Видео:№693. В прямоугольный треугольник вписана окружность радиуса r. Найдите периметр треугольника,Скачать
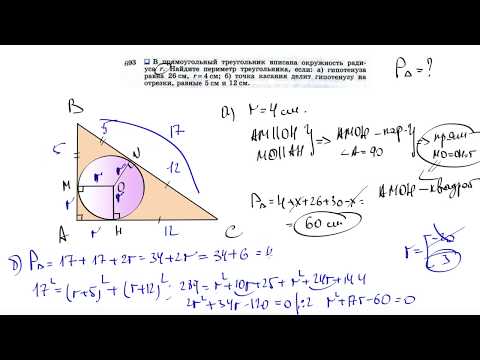
Катеты прямоугольного треугольника 18 и 24?
Катеты прямоугольного треугольника 18 и 24.
Найти гипотенузу и радиус описанной окружности.
На этой странице находится ответ на вопрос Найдите радиус описанной окружности если гипотенуза прямоугольного треугольника равна 1) 25 см 2) 41 дм 3) 130мм 4) 61 см?, из категории Геометрия, соответствующий программе для 5 — 9 классов. Чтобы посмотреть другие ответы воспользуйтесь «умным поиском»: с помощью ключевых слов подберите похожие вопросы и ответы в категории Геометрия. Ответ, полностью соответствующий критериям вашего поиска, можно найти с помощью простого интерфейса: нажмите кнопку вверху страницы и сформулируйте вопрос иначе. Обратите внимание на варианты ответов других пользователей, которые можно не только просмотреть, но и прокомментировать.
Р прямоугольника = 2 * ( 32 + 28) = 2 * 60 = 120 см т. К. у квадрата все стороны равны, то периметр делим на 4 (количество сторон) 120÷ 4 = 30 см длина стороны квадрата.
А) да, параллельны, потому что сумма внутренних углов равна 180° Б) да, по той же причине В) 180° — 130° = 50°.
РЕШЕНИЕ СМОТРИ НА ФОТОГРАФИИ.
Биссектриса KE, проведенная из вершины острого угла прямоугольного треугольника KPT( угол P = 90) к катету PT, Делит катет в отношении 5 : 13. Найдите косинус угла KTP.
2. ∠ABN = 180° — ∠CBK — ∠KBN = 180 — 30 — 50 = 100° ∠ABM = 1 / 2 * ∠ABN = 100 : 2 = 50° — ОТВЕТ С. 6. ∠AOC = ∠BOD — как накрестлежащие в пересекающихся прямых. ТреугольникиΔAOC иΔDOBравны по двум углам и стороне. CA = BD = 10 см — ОТВЕТ.
180 — 80 = 100 180 — 50 = 130 Ответ 130 100.
Решение задания смотри на фотографии.
ΔDNR — прямоугольный, т. К. ND — высота, ∠DRN = 30°⇒по теореме DN = 1 / 2 * NR⇒NR = 2 * DN = 3 * 2 = 6 см NR = MK = 6cм по свойству противолежащих сторон параллелограмма, MN = KR = 5см по свойству противолежащих сторон параллелограмма. P = 2 * MN +..
Угол АВС = углу BDE = 127° уголBEA = углуBDC = 90° четырехугольник MEBD(Сумма углов в четырехугольнике равна 360° угол EMB = 360° — 90° — 90° — 127° = 53° Ответ : 53°.
∠ABC = ∠EBD = 127° — как вертикальные. ∠DME = 360° — ∠MEC — ∠MDA — ∠EBD = 360° — 90° — 90° — 127° = 53°. Ответ : 53°.
Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать
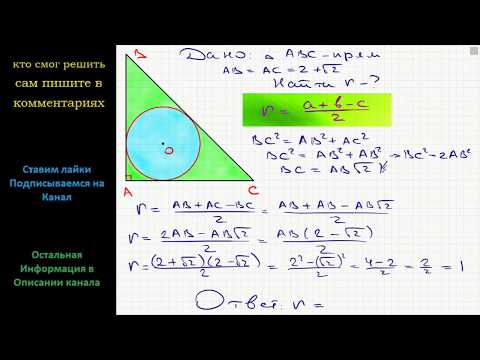
Радиус вписанной окружности в прямоугольный треугольник онлайн
С помощю этого онлайн калькулятора можно найти радиус вписанной в любой треугольник окружности, в том числе радиус вписанной в прямоугольный треугольник окружности. Для нахождения радиуса вписанной в треугольник окружности выберите тип треугольника, введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Видео:ОГЭ Задание 25 Площадь описанного прямоугольного треугольникаСкачать

1. Радиус вписанной в прямоугольный треугольник окружности, если известны катеты треугольника
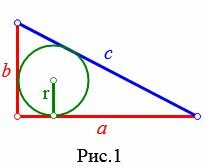
Пусть известны катеты a и b прямоугольного треугольника (Рис.1). Выведем формулу вычисления радиуса вписанной в треугольник окружности.
 |
Радиус вписанной в треугольник окружности, если известна площадь треугольника S и полупериметр p вычисляется из следующей формулы (статья Радиус вписанной в треугольник окружности, формула (5)):
| ( small r= frac, ) | (1) |
| ( small p= frac. ) | (2) |
Площадь прямоугольного треугольника по катетам вычисляется из формулы:
| ( small S= large frac small cdot a cdot b. ) | (3) |
Подставляя (2) и (3) в (1) получим формулу вписанной в прямоугольный треугольник окружности:
| ( small r= large frac<fracab><frac(a+b+c)> ) ( small = large frac, ) | (4) |
| ( small c= sqrt. ) | (5) |
Из формулы (4) выведем другую эквивалентную формулу. Умножим числитель и знаменатель формулы (4) на ( small a+b-c ):
| ( small r= frac ) ( small = frac ) ( small = frac ) | (6) |
Учитывая (5), формулу (6) можно переписать так:
| ( small r= frac ) ( small = frac .) |
Таким образом другая формула вычисления радиуса вписанной в треугольник окружности имеет вид:
| ( small r= frac ,) | (7) |
где c вычисляется из (5).
Пример 1. Известны катеты прямоугольного треугольника a=17 и b=5. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся одним из формул (4) и (7). Вычислим, сначала, гипотенузу прямоугольного треугольника из формулы (5):
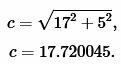 |
Подставим значения ( small a=17, ; b=5; c=17.720045 ) в (7):
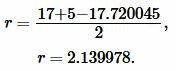 |
Ответ:
Видео:Математика ОГЭ Задание 26 Прямоугольный треугольник Описанная и вписанная окружностиСкачать

2. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и прилегающей к нему острый угол
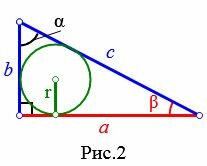
Пусть известны катет a прямоугольного треугольника и прилежащий к нему угол β(Рис.2). Выведем формулу радиуса вписанной в треугольник окружности.
 |
| ( small frac=frac .) |
Учитывая, что ( small alpha=90°-beta ) и ( small sin (90°-beta)=cos beta ), получим:
| ( small frac=frac ) ( small =frac=frac .) | (8) |
Тогда из (8) получим:
| ( small b=frac. ) | (9) |
Далее, из теоремы синусов:
| ( small frac=frac ) ( small =frac=frac .) |
| ( small c=frac .) | (10) |
Чтобы получить формулу радиуса вписанной в прямоугольный треугольник окружности через катет и прилежащий к нему угол, подставим значения ( small b ) и ( small c ) из (9) и (10) в (7):
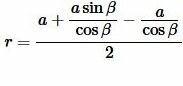 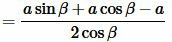 |
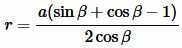 | (11) |
Пример 2. Известны катет ( small a=21 ) и прилежащий к нему угол ( small beta=30° ) прямоугольного треугольника. Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (11). Подставим значения ( small a=21 ) ( small beta=30° ) в (11):
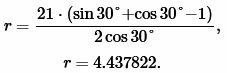 |
Ответ:
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

3. Радиус вписанной в прямоугольный треугольник окружности, если известны катет и противолежащий острый угол
Пусть известны катет a прямоугольного треугольника и противолежащий угол ( small alpha; ) (Рис.3). Найдем формулу радиуса вписанной в треугольник окружности.
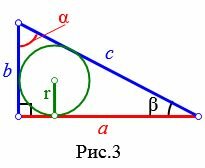 |
В предыдущем параграфе мы вывели формулу вписанной в прямоугольный треугольник окружности по катету и прилежащему углу (формула (11)). Учитывая, что в прямоугольном треугольнике сумма острых углов равна 90°, имеем:
| ( small alpha+beta=90°) ( small beta=90°-alpha ) |
Тогда (11) можно преобразовать так (подробнее на странице Формулы приведения тригонометрических функций:
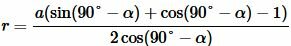 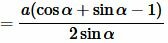 |
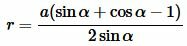 | (12) |
Пример 3. Известны катет ( small a=6 ) прямоугольного треугольника и противолежащий угол ( small alpha=53°. ) Найти радиус окружности вписанной в треугольник.
Решение. Для нахождения радиуса окружности вписанной в треугольник воспользуемся формулой (12). Подставим значение ( small a=6, ; alpha=53° ) в (12):
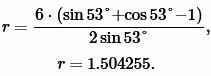 |
Ответ: