Радиус через радиус вектор

Радиус-вектор — вектор, проведенный из начала координат в место расположения данной точки.

Следует заметить важную формулу

$overrightarrow <> $=r₂—r₁

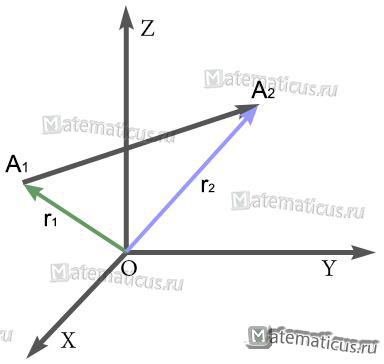
где r₁=$overrightarrow <> $ радиус-вектор начала А₁, вектора $overrightarrow <> $, r₂=$overrightarrow <> $ — радиус-вектор его конца А₂.
X, Y, Z — координаты вектора $overrightarrow <> $,
X₁, Y₁, Z₁ — координаты точки А₁ (они соответственно равны координатам радиуса-вектора r₁=$overrightarrow <> $) и X₂, Y₂, Z₂ — координаты точки А₂, (они соответственно равны координатам радиуса-вектора r₂=$overrightarrow <> $).
Таким образом, чтобы найти абсциссу вектора, надо из абсциссы конца вычесть абсциссу начала вектора.
Аналогичные правила для ординаты и аппликаты.

Пример
Найти координаты вектора $overrightarrow <> $, если А₁(1;-2;5) и А₂(-2;4;0).

Решение
X=-2-1=-3, Y=4-(-2)=6, Z=0-5=-5, так что $overrightarrow <> $=

Видео:2.4. Радиус-вектор и вектор перемещенияСкачать

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Видео:Радиус векторСкачать

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Видео:Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Видео:Лекция 4. ВЕКТОРА │ кинематика с нуляСкачать

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Видео:10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Видео:Радиус-векторыСкачать

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Видео:ЕГЭ по Физике 2022. Кинематика. Радиус-векторСкачать

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Видео:Определение параметров движения по заданному радиус-вектору. Векторный способ задания движения.Скачать

Физика

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Видео:9 класс геометрия 8 урок Радиус вектор точки геометрияСкачать

Механическое движение. Система отсчёта. Закон относительности движения

Механическим движением в физике называется изменение с течением времени положения тела (или его частей) в пространстве относительно других тел.

То есть, чтобы сказать, что тело или система совершает механическое движение, нам необходимо: 1) наблюдать его во времени; 2) сравнивать его положение с положением какого-то другого тела (относительно этого тела).

Например, пассажир в едущем автомобиле неподвижен относительно кресла, на котором он сидит, но он движется относительно людей, стоящих на автобусной остановке и самой остановки. А сама автобусная остановка неподвижна относительно стоящих людей, ждущих автобус (см. рисунок 1). Однако она движется относительно проезжающих мимо машин. В первом случае наблюдаемым объектом был человек в машине, а точкой отсчета кресло и люди на остановке. Во втором случае наблюдаемой была автобусная остановка, а точками отсчета – люди на остановке и проезжающие мимо машины.

Рисунок 1 – Иллюстрация к примеру

Из примеров можно сделать вывод, что важно, какой именно объект находится под наблюдением и относительно какого объекта – тела отсчета – рассматривается его движение. Отсюда можно сформулировать закон относительности движения: характер движения тела зависит от того, относительно какого объекта мы рассматриваем данное движение.

Тело (или точка) отсчета, связанная с ним система координат и часы, вместе образуют систему отсчета. То есть все сказанное выше можно переформулировать в одно предложение: для наблюдения механического движения важно в какой системе отсчета будет происходить наблюдение.

Рисунок 2 – Пример системы отсчета (наблюдаемы объект – летящий мяч, тело отсчета – камень, лежащий в начале координат, система координат и секундомер для отсчета времени)

Однако объекты могут быть очень сложными для наблюдения. Например, автомобиль едет по прямой несколько километров и необходимо описать его движение относительно камня на обочине. Казалось бы, все просто. Но как именно описать движение автомобиля, если корпус его движется по прямой, а колеса совершают вращательные движения.

Для удобства решения подобных задач принято упрощение: если размер и форма тела в данной задаче не играют важной роли для наблюдателя, можно считать это тело за материальную точку.

Материальная точка – это такое тело, размером и формой которого в условиях данной задачи можно пренебречь.

Приведем пример: когда автобус едет из города А в город Б, его можно рассматривать как материальную точку. Когда пассажир идет из одного конца этого автобуса в другой, считать автобус материальной точкой нельзя. В общем случае можно сказать, что тело можно считать материальной точкой, если его размеры значительно меньше расстояния, на которое оно перемещается.

Видео:Радиус-вектор и перемещение. Кинематика.Скачать

Уравнения движения. Радиус-вектор. Проекция вектора

Для описания движения тела необходимо уметь рассчитывать его положение в каждый момент времени. Как это сделать?

Самый очевидный способ – координатный. Если вернуться к примеру на рисунке 2, можно увидеть, что летящий мяч в каждый момент времени имеет три координаты по осям OX, OY и OZ. Эти координаты являются функциями времени (т.е. они зависят от времени), а значит, их можно записать в виде системы:

Вид этих уравнений будет зависеть от многих вещей: от того, с какой силой бросили мяч в начале, от массы мяча, под каким углом его бросили и так далее. В любом случае, если эти уравнения заданы, можно найти координаты (то есть положение) тела в любой момент времени. Поиск этих уравнений – основная задача кинематики.

Эта система является кинематическими уравнениями движения тела или материальной точки, записанными в координатной форме. Повторим: если вид уравнений движения задан, можно узнать координату движущейся точки в любой момент времени.

В общем случае, координат три, но иногда можно обойтись двумя или даже одной координатой. Например, для описания движения бильярдного шара достаточно двух координат (так как шар не может двигаться вверх и вниз), а для описания движения шарика, катящегося по прямому горизонтальному желобку достаточно одной координаты (шарик не может двигаться вверх-вниз и вправо-влево).

Еще один способ описания движения – векторный.

*Перед дальнейшим прочтением данной статьи желательно вспомнить основную теорию по теме «Векторы» и «Метод координат»

Вектор, проведенный из начала координат к материальной точке, называется радиус-вектором (см. рисунок 3).

Рисунок 3 – Радиус-вектор (серой линией изображены траектория движения материальной точки, r₁ и r₂* радиус-векторы, проведенные к этой материальной точке в разные моменты времени)

Радиус-вектор проведенный к материальной точке в разные моменты времени будет разным. Значит, его тоже можно представить, как функцию времени:

r = r(t)

Такая функция и будет уравнением движения в векторной форме. Если ее вид задан, можно описать движение тела с той же полнотой, как и при координатной записи.

Еще раз обозначим отличия: при записи уравнения движения в координатной форме в каждый момент времени наблюдающий будет знать три координаты тела; при записи в векторной форме в каждый момент времени известен радиус-вектор (его модуль и направление). Обе записи равносильны.

*На письме векторы обычно обозначаются стрелкой сверху, над величиной. Однако в печатном тексте не всегда удобно нагромождать формулы дополнительными знаками, поэтому в печати векторные величины пишут просто жирным шрифтом. В данной статье далее жирным шрифтом будут написаны только векторные величины.

Покажем, что векторная и координатная записи равносильны. Для этого необходимо вспомнить, как построить проекцию вектора на ось (см. рисунок 4).

Рисунок 4 – Построение проекции вектора на ось

Чтобы построить проекцию вектора на ось, необходимо опустить перпендикуляра из начала и конца вектора на эту ось. Длина получившегося отрезка между проекциями начала и конца вектора, взятая со знаком «+», если вектор а сонаправлен с осью Х, или со знаком «-», если вектор а противонаправлен оси Х, — это и есть искомая проекция.

Если вектор выходит из начала координат, задача облегчается – необходимо опустить перпендикуляр только из конца вектора.

Напоминания из геометрии:

два вектора равны, если они параллельны или лежат на одной прямой, сонаправлены, а их модули равны;

проекции равных векторов равны.

Рассмотрим пример (см. рисунок 5)

Рисунок 5 – Задача на нахождение проекции векторов

Предлагаем читателю самому подумать, а затем сравнить свои рассуждения с приведенными ниже.

Итак, вектор а: его начала соответствует координате х_н=1, а конец х_к = 4. Значит a_x = х_к – х_н = 4-1 = 3. Вектор b: его начало лежит в точке х_н=2, а конец х_к =0. Значит b_x = х_к – х_н = 0-2 = -2.

В двумерном случае, проецировать нужно на две оси, но принцип остается тем же.

Иногда еще нужно находить составляющие компоненты вектора а_х и а_у. Рассмотрим пример, для простоты возьмем вектор, выходящий из начал координат (см. рисунок 6).

Сумма векторов а_х и а_у равна а. Модули векторов а_х и а_у численно равны координатам точек, куда попали перпендикуляры, опущенные из конца вектора а на оси ОХ и ОУ.

Еще следует отметить, что, если известен угол β между вектором а и осью ОХ, воспользовавшись основами тригонометрии, можно найти величины проекций:

Если бы вектор а совпадал с радиус-вектором какой-нибудь точки, то величины а_х и а_у совпадали бы с координатами тела по осям ОХ и ОY.

Способ с использованием тригонометрических функций удобен, когда координата конца вектора попадает в нецелое число и опустив перпендикуляр на ось его трудно найти точно. В физических задачах такое часто случается.

Рисунок 6 – Нахождение компонент вектора а

Рассмотрим пример (см. рисунок 7). Модуль вектора r равен 2. Сам вектор направлен под углом в 45 градусов к оси ОХ. Необходимо найти величины проекций (они же координаты) этого вектора на оси ОХ и ОУ.

Рисунок 7 – Задача на нахождение проекций вектора в двумерном пространстве

В общем случае радиус-вектор находится в трехмерном пространстве (см. рисунок 8). Построение проекции осуществляется по тому же принципу, что и в рассмотренных выше примерах. Когда строятся проекции на оси ОХ и ОУ, перпендикуляр сначала опускается на плоскость, в которой лежат оси ОХ и ОУ, а затем точка, в которую упал перпендикуляр к плоскости, проецируется на оси ОХ и ОУ.

Точки, в которые попал перпендикуляры к осям – r_x, r_y, r_z – это и есть координаты x, y, z тела в текущий момент времени.

Следует оговориться, что большинство задач 10-го класса будут ограничиваться двумерным пространством.

Рисунок 8 – Построение проекций радиус-вектора

Видео:Модель материальной точки. Радиус вектор | ФизикаСкачать

Траектория. Путь. Перемещение

Траектория – это линия, вдоль которой движется тело.

Траектория движения может быть прямолинейной, если тело движется по прямой линии, и криволинейной, если тело движется по кривой.

Путь (S), пройденный телом, равен длине траектории.

Перемещение (r)* – это вектор, проведенный из начала пути в конец.

В случае прямолинейного движения путь и модуль перемещения тела совпадают (см. рисунок 9а). В случае криволинейного – путь и перемещение различаются (см. рисунок 9б), так как длина линии движения тела больше длины вектора, соединяющего начало и конец траектории.

Рисунок 9 – Путь (S) и перемещение (r) при прямолинейном (а) и криволинейном (б) движении

*Иногда перемещение так же, как и путь, называют буквой S — (на письме с вектором над ней, при печати — жирным шрифтом, так как это векторная величина). В данной статье, чтобы не путаться, перемещение называется только буквой r. В целом, обозначения равноправны, поэтому при решении задач можно использовать то, которое удобнее. Однако не стоит забывать отмечать, что именно обозначено под той или иной буквой.

Видео:Радиус вектор точки геометрияСкачать

Равномерное прямолинейное движение: скорость и уравнение движения

Путь и перемещение при равномерном прямолинейном движении

Прямолинейное равномерное движение уже рассматривалось в курсе физики ранее, однако приведем основные определения.

Прямолинейное движение – это движение по прямой линии. Равномерное движение – такое, в процессе которого тело за равные временные промежутки проходит один и тот же путь. Если объединить эти два определения получится третье:

• равномерное прямолинейное движение – это такое движение, в ходе которого 1) тело совершает движение по прямой линии; 2) за одинаковые временные промежутки проходит одинаковый путь.

Зная определения пути и перемещения, это определение можно упростить: прямолинейное равномерное движение тела – это такое движение, в процессе которого тело за одинаковые временные промежутки совершает равные перемещения.

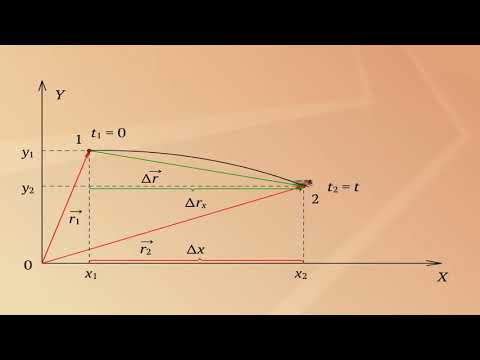
Важной характеристикой является скорость механического движения. Предположим, что при равномерном прямолинейном движении тело за промежуток времени △t перемещается из точки А в точку Б (см. рисунок 8). Радиус-вектор, проведенный в точку A обозначим r₀, а радиус-вектор в точку Б обозначим r₁. Изменение радиус-вектора назовем △r – нетрудно заметить, что это есть перемещение тела за время △t.

Рисунок 8 – Поиск перемещения тела через радиус-векторы при равномерном прямолинейном движении

Тогда скорость движения (v) будет вычисляться по формуле:

Так как △r – вектор, △t – скаляр, скорость v тоже будет вектором, сонаправленным перемещению.

Если тело начинает двигаться в момент начала отсчета, то △t = t*. Из правила сложения векторов следует, что △r = r₁ — r₀. Тогда выражение для скорости можно переписать в виде:

Из этого выражения следует:

Это выражение можно применить к любому произвольно взятому моменту времени, поэтому можно опустить индекс в левой части и переписать:

Данное уравнение является уравнением движения при прямолинейном равномерном движении.

*Напоминание: символом △ (дельта) обозначают изменение какой-нибудь величины. Например △t = t – t₁, где t – конечный момент времени, t₁ – начальный. Если же начальный момент времени совпадает с началом отсчета t₁ = 0, то △t = t – 0 = t_.

Фактически уравнение равномерного прямолинейного движения означает, что радиус-вектор в произвольный момент времени t можно посчитать, сложив начальный радиус-вектор и приращение v*t.

Найдя проекции радиус-вектора и вектора скорости, можно разложить уравнение движения тела на три составляющие вдоль осей ОX, ОY и ОZ.

В этих выражениях r_0x, r_0y, r_0z и v_x, v_y, v_z – это компоненты изначальных векторов r₀ и v вдоль осей ОХ, ОY и ОZ соответственно. И теперь можно перейти к скалярному виду:

Стоит отметить, что при проецировании какие-то компоненты вектора могут стать отрицательными, тогда знаки в выражениях поменяются на противоположные.

В рассмотренном выше примере движение происходит только вдоль оси ОХ (остальные координаты не изменяются). На рисунке 9 приведены проекции начальной (х₀) и конечной (х₁) точки на ось ОХ.

Рисунок 9 – Перемещение тела в координатном представлении

Уравнение координаты (х) движения будет выглядеть:

А это уже похоже на знакомую из прошедшего курса физики формулу для нахождения пути:

Если точка начала двигаться из начала отсчета S₀ = 0, можно переписать эту формулу в виде:

Отсюда следуют известные уже формулы для нахождения скорости и времени при равномерном прямолинейном движении:

Приведем последний в этой статье пример: известно, что тело движется вдоль оси ОХ, начиная из точки x₀ = 3 см. Скорость тела равна v = 5 м/с и направлена вдоль оси ОХ. Необходимо записать уравнение движения по координате х для этого тела.

Итак, для начала приведем все единицы измерения к СИ:

Теперь можно записывать уравнение для координаты х:

Из этого уравнения можно найти координату тела в любой момент времени. Например, через 2 секунды после начала отсчета тело находилось в точке:

x(2) = 0,03 + 5*2 = 10, 03.

А какой путь прошло тело к этому моменту? В начале оно находилось в точке x(2) = 0,03 м, а через 2 секунды оно стало находиться в точке x(2) = 10, 03. Значит за 2 секунды тело прошло:

S = x(2) – x₀ = 10, 03 – 0,03 = 10 м.

А если скорость тела была направлена противоположно оси ОХ, как тогда выглядело бы уравнение движения?

Тогда проекция вектора скорости на ось ОХ была бы отрицательной и в уравнении знак перед скоростью поменялся бы на противоположный:

📽️ Видео

Перемещение как изменение радиус-вектораСкачать

ротор от радиус вектора на модуль радиус вектораСкачать

Демидович №4441б: поток радиус-вектора через замкнутую поверхностьСкачать

10 Класс - Физика - Перемещение. Радиус-вектор.Скачать

ЧТО ТАКОЕ РАДИУС ВЕКТОР В МАТЕМАТИКЕ?Скачать

1.1. Радиус-вектор. ЕГЭ по физике.Скачать

Координаты вектора. 9 класс.Скачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать