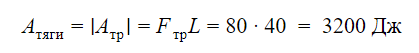Работа вектор или скаляр (5 видео) | Курс школьной геометрии

Механическая работа

О чем эта статья:

Для нас привычно понятие «работа» в бытовом смысле. Работая, мы совершаем какое-либо действие, чаще всего полезное. В физике (если точнее, то в механике) термин «работа» показывает, какую силу в результате действия приложили, и на какое расстояние тело в результате действия этой силы переместилось.

Например, нам нужно поднять велосипед по лестнице в квартиру. Тогда работа будет определяться тем, сколько весит велосипед и на каком этаже (на какой высоте) находится квартира.

Механическая работа — это физическая величина, прямо пропорциональная приложенной к телу силе и пройденному телом пути.

Чтобы рассчитать работу, нам необходимо умножить численное значение приложенной к телу силы F на путь, пройденный телом в направлении действия силы S. Работа обозначается латинской буквой А.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

Если под действием силы в 1 ньютон тело переместилось на 1 метр, то данной силой совершена работа в 1 джоуль.

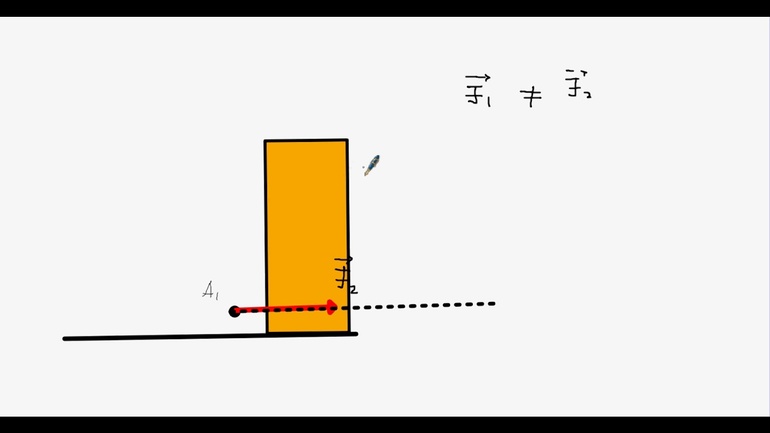
Поскольку сила и путь — векторные величины, в случае наличия между ними угла формула принимает вид.

Механическая работа

А = FScosα

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

α — угол между векторами силы и перемещения []

Числовое значение работы может становиться отрицательным, если вектор силы противоположен вектору скорости. Иными словами, сила может не только придавать телу скорость для совершения движения, но и препятствовать уже совершаемому перемещению. В таком случае сила называется противодействующей.

Для совершения работы необходимы два условия:

чтобы на тело действовала сила,
чтобы происходило перемещение тела.

Сила, действующая на тело, может и не совершать работу. Например, если кто-то безуспешно пытается сдвинуть с места тяжелый шкаф. Сила, с которой человек действует на шкаф, не совершает работу, поскольку перемещение шкафа равно нулю.

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Содержание

Полезная и затраченная работа
И как же достоверно определить, какая работа полезная, а какая затраченная?
Мощность
Примеры решения задач
Задача 1
Задача 2
Задача 3
Задача 4
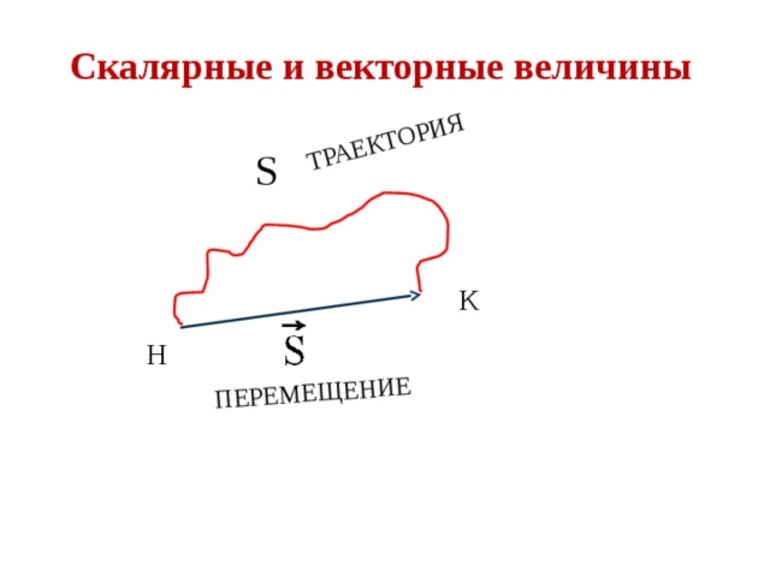
Скалярные и векторные величины в физике и математике
Особенности скалярных величин
Определение положительного скаляра и его измерения
Особенности векторных величин
Свойства векторов
Работа — скалярная величина или векторная?
Ваш ответ
решение вопроса
Похожие вопросы
🌟 Видео

Видео:Физика | Ликбез по векторамСкачать

Полезная и затраченная работа

Был такой мифологический персонаж у древних греков — Сизиф. За то, что он обманул богов, те приговорили его после смерти вечно таскать огромный булыжник вверх по горе, откуда этот булыжник скатывался — и так без конца. В общем, Сизиф делал совершенно бесполезное дело с нулевым КПД. Поэтому бесполезную работу и называют «сизифов труд».

Чтобы разобраться в понятиях полезной и затраченной работы, давайте пофантазируем и представим, что Сизифа помиловали и камень больше не скатывается с горы, а КПД перестал быть нулевым.

Полезная работа в этом случае равна потенциальной энергии, приобретенной булыжником. Потенциальная энергия, в свою очередь, прямо пропорциональна высоте: чем выше расположено тело, тем больше его потенциальная энергия. Выходит, чем выше Сизиф прикатил камень, тем больше полезная работа.

Потенциальная энергия

Е_п = mgh

m — масса тела [кг]

g — ускорение свободного падения [м/с 2 ]

h — высота [м]

На планете Земля g ≈ 9,8 м/с 2

Затраченная работа в нашем примере — это механическая работа Сизифа. Механическая работа зависит от приложенной силы и пути, на протяжении которого эта сила была приложена.

Механическая работа

А = FS

A — механическая работа [Дж]

F — приложенная сила [Н]

S — путь [м]

И как же достоверно определить, какая работа полезная, а какая затраченная?

Все очень просто! Задаем два вопроса:

За счет чего происходит процесс?
Ради какого результата?

В примере выше процесс происходит ради того, чтобы тело поднялось на какую-то высоту, а значит — приобрело потенциальную энергию (для физики это синонимы).

Происходит процесс за счет энергии, затраченной Сизифом — вот и затраченная работа.

Мощность

На заводах по всему миру большинство задач выполняют машины. Например, если нам нужно закрыть крышечками тысячу банок колы, аппарат сделает это в считанные минуты. У человека эта задача заняла бы намного больше времени. Получается, что машина и человек выполняют одинаковую работу за разные промежутки времени. Для того, чтобы описать скорость выполнения работы, нам потребуется понятие мощности.

Мощностью называется физическая величина, равная отношению работы ко времени ее выполнения.

Мощность

N = A/t

N — мощность [Вт]

A — механическая работа [Дж]

t — время [с]

Один ватт — это мощность, при которой работа в один джоуль совершается за одну секунду.

Также для мощности справедлива другая формула:

Мощность

N = Fv

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

Как и для работы, для мощности справедливо правило знаков: если векторы направлены противоположно, значение мощности будет отрицательным.

Поскольку сила и скорость — векторные величины, в случае наличия между ними угла формула принимает следующий вид:

Мощность

N = Fvcosα

N — мощность [Вт]

F — приложенная сила [Н]

v — скорость [м/с]

α — угол между векторами силы и скорости []

Видео:Скалярные и векторные величины, основные определения.Скачать

Примеры решения задач

Задача 1

Ложка медленно тонет в большой банке меда. На нее действуют сила тяжести, сила вязкого трения и выталкивающая сила. Какая из этих сил при движении тела совершает положительную работу? Выберите правильный ответ:

Выталкивающая сила.
Сила вязкого трения.
Сила тяжести.
Ни одна из перечисленных сил.

Решение

Поскольку ложка падает вниз, перемещение направлено вниз. В ту же сторону, что и перемещение, направлена только сила тяжести. Это значит, что она совершает положительную работу.

Ответ: 3.

Задача 2

Ящик тянут по земле за веревку по горизонтальной окружности длиной L = 40 м с постоянной по модулю скоростью. Модуль силы трения, действующей на ящик со стороны земли, равен 80 H. Чему равна работа силы тяги за один оборот?

Решение

Поскольку ящик тянут с постоянной по модулю скоростью, его кинетическая энергия не меняется. Вся энергия, которая расходуется на работу силы трения, должна поступать в систему за счет работы силы тяги. Отсюда находим работу силы тяги за один оборот:

Ответ: 3200 Дж.

Задача 3

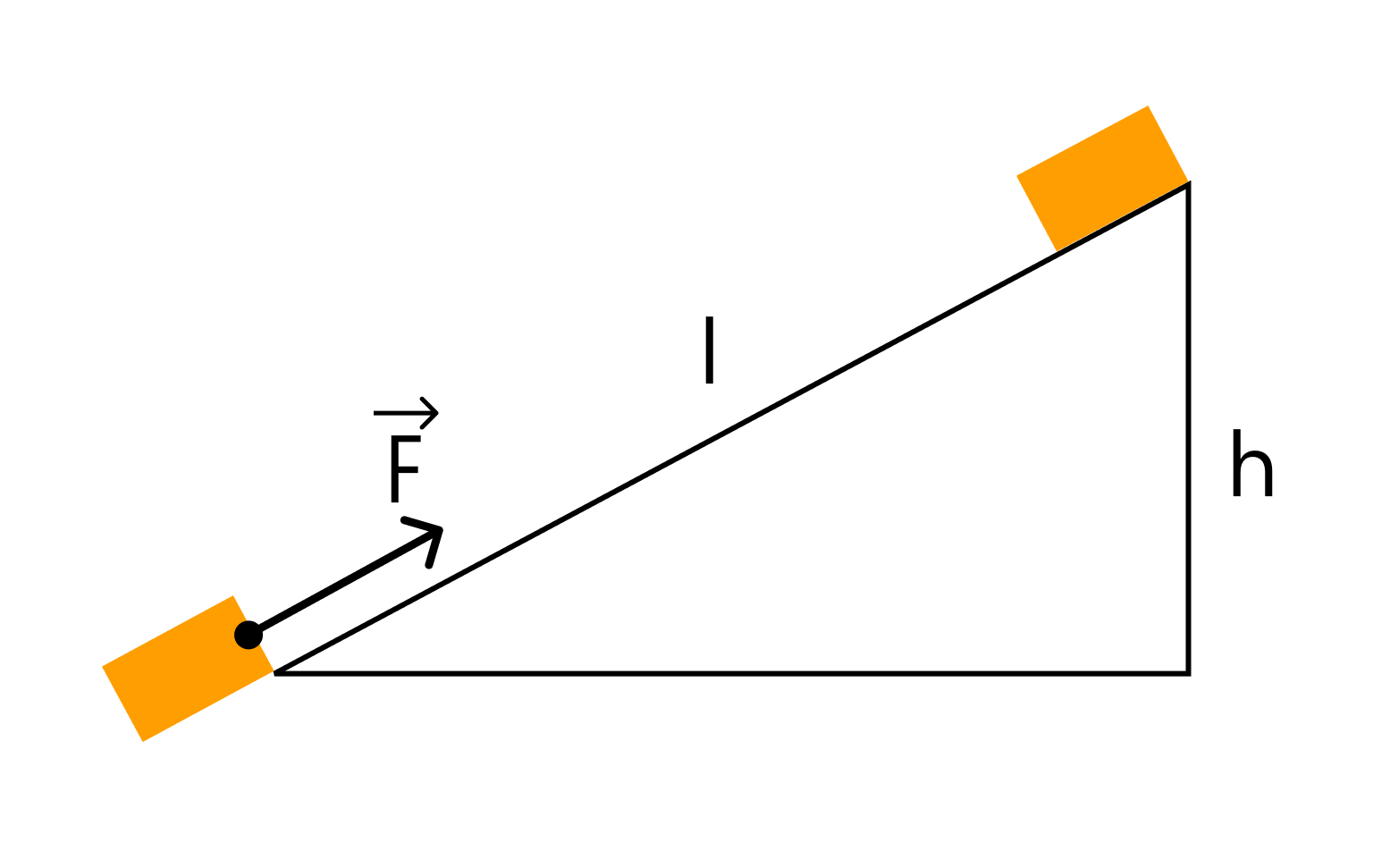
Тело массой 2 кг под действием силы F перемещается вверх по наклонной плоскости на расстояние l = 5 м. Расстояние тела от поверхности Земли при этом увеличивается на 3 метра. Вектор силы F направлен параллельно наклонной плоскости, модуль силы F равен 30 Н. Какую работу при этом перемещении в системе отсчета, связанной с наклонной плоскостью, совершила сила F?

Решение

В данном случае нас просят найти работу силы F, совершенную при перемещении тела по наклонной плоскости. Это значит, что нас интересуют сила F и пройденный путь. Если бы нас спрашивали про работу силы тяжести, мы бы считали через силу тяжести и высоту.

Работа силы определяется как скалярное произведение вектора силы и вектора перемещения тела. Следовательно:

A = Fl = 30 * 5 = 150 Дж

Ответ: 150 Дж.

Задача 4

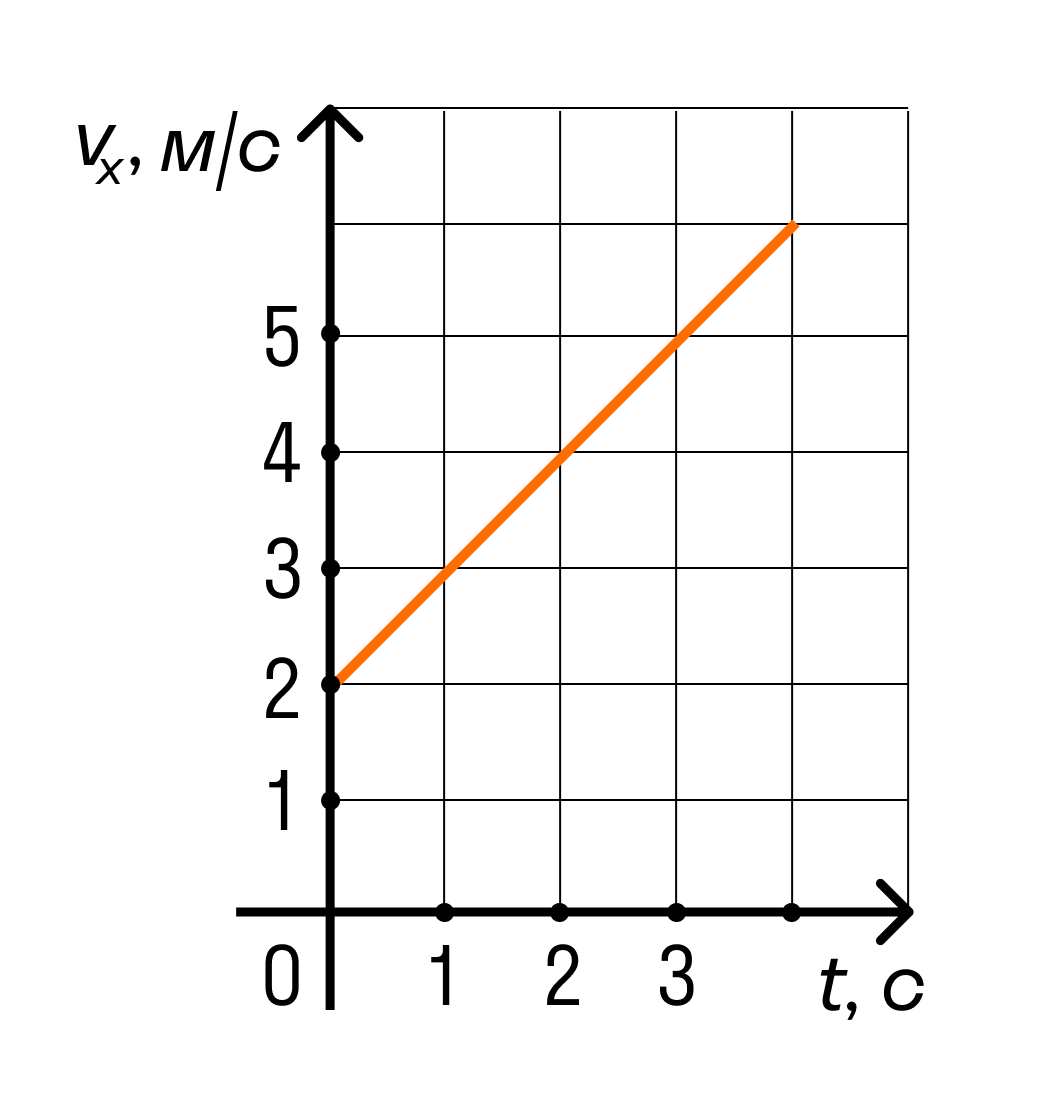
Тело движется вдоль оси ОХ под действием силы F = 2 Н, направленной вдоль этой оси. На рисунке приведен график зависимости проекции скорости v x тела на эту ось от времени t. Какую мощность развивает эта сила в момент времени t = 3 с?

Решение

На графике видно, что проекция скорости тела в момент времени 3 секунды равна 5 м/с.

Мощность можно найти по формуле N = Fv.

N = FV = 2×5 = 10 Вт

Ответ: 10 Вт.

Попробуйте онлайн-курс подготовки к ЕГЭ по физике с опытным преподавателем в Skysmart!

Видео:Скалярное произведение векторов. 9 класс.Скачать

Скалярные и векторные величины в физике и математике

Видео:Урок 8. Векторные величины. Действия над векторами.Скачать

Особенности скалярных величин

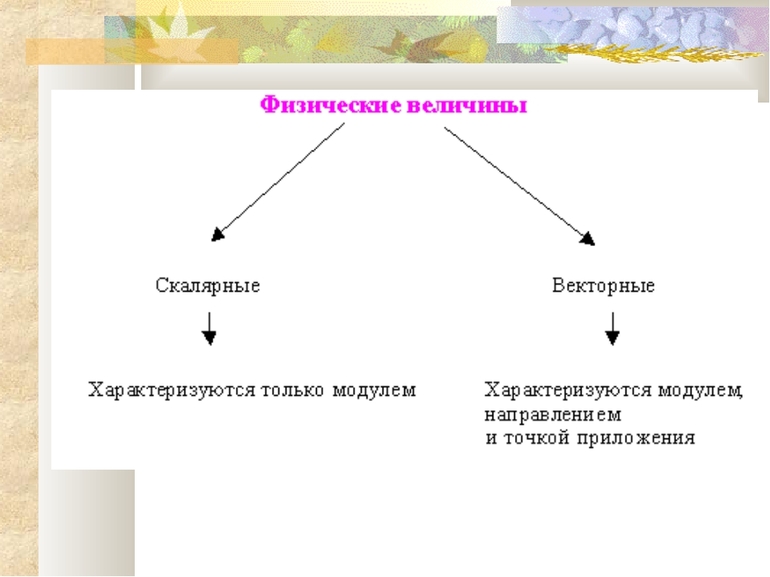
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:

Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.

В физике в список скалярных величин входят:

Масса — определяет величину материи и ее гравитационные свойства. Измеряется в килограммах и обозначается буквой латинского алфавита m.
Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
Время — продолжительность действия или события. Рассчитывается в секундах.
Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон. Измеряется в м 3 .
Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда. Обозначается буквой U и рассчитывается в Вольтах.
Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
Энергия — обозначает способность тела осуществлять работу.

Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.

Видео:Введение в векторы и скаляры (видео 1)| Векторы. Прямолинейное движение | ФизикаСкачать

Определение положительного скаляра и его измерения

Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.

Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).

Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать

Особенности векторных величин

Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.

В физике и математике примерами векторных величин являются:

Сила — мера взаимодействия физических веществ. Обозначается латинской буквой F и измеряется в Ньютонах. Три закона Исаака Ньютона составляют основу классической механики. С их помощью можно определить массу тела и его ускорение.
Скорость — расстояние, пройденное материей за определенный временной промежуток. Маркируется символом V и рассчитывается в м/с. Скорость используется для определения пути и времени движения предмета при помощи формулы: S = V * t. Скорость, с которой тело движется по окружности, называется линейной.
Ускорение — величина, показывающая изменение показателей скорости физического тела. Ускорение свободного падения действует на все тела, придавая им силу тяжести. Оно направлено к ядру Земли и равняется 9,8 м/с 2
Импульс — характеризует величину движения тела. Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.

На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Свойства векторов

Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:

Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.

Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.

Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.

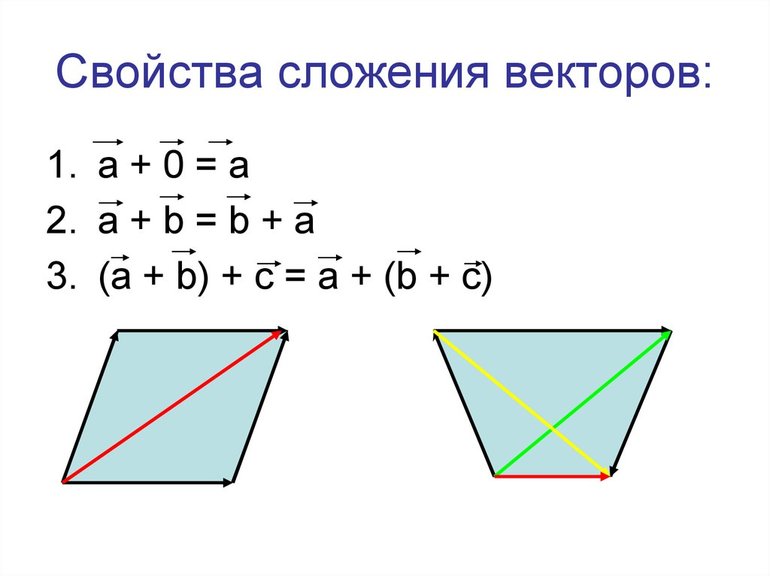
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.

Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.

Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.

Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.

Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать