Р множество трапеций q множество четырехугольников имеющих прямой угол (5 видео)

Лекция 2. Отношение между множествами.

Содержание

«Календарь счастливой жизни: инструменты и механизм работы для достижения своих целей»
Р множество трапеций q множество четырехугольников имеющих прямой угол
Правила построения отрицаний.
📽️ Видео

Видео:Множества и операции над нимиСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Лекция 2. Отношения между множествами.

Между двумя множествами существует пять видов отношений.

Если множества А и В не имеют общих элементов, то говорят, что эти множества не пересекаются и записывают этот факт в виде А∩В = ∅ . Например, А = < a , c , k >, В = < d , e , m , n >, общих элементов у этих множеств нет, поэтому множества не пересекаются.

Если множества А и В имеют общие элементы, т.е. элементы, принадлежащие одновременно А и В, то говорят, что эти множества пересекаются и записывают А∩В≠ ∅ . Например, множества А = < a , c , k > и В = < c , k , m , n > пересекаются, т. к. у них есть общие элементы c , k .

Множество В является подмножеством множества А, если каждый элемент множества В является также элементом множества А. Пустое множество является подмножеством любого множества. Само множество является подмножеством самого себя. (пишут В ⊂ А)

Пустое множество и само множество называют несобственными подмножествами . Остальные подмножества множества А называются собственными. Для каждого множества, состоящего из n элементов можно образовать 2 n подмножеств. Если рассматривают лишь подмножества некоторого множества U, то U называют универсальным множеством.

Если множества А и В состоят из одних и тех же элементов, то они называются равными.

Например, А = < a , c , k , m , n > и В = < m , n , a , c , k >, А = В.

Существует пять случаев отношений между двумя множествами. Их можно наглядно представить при помощи особых чертежей, которые называются кругами или диаграммами Эйлера-Венна.

Разбиение множества на классы называют классификацией.

Классификацию можно выполнять при помощи свойств элементов множества. Если выбирается только одно свойство, то такую классификацию называют дихотомической . Например, натуральные числа можно разбить на четные и нечетные. Буквы русского языка можно разбить на гласные и не гласные. Вообще, если на множестве Х задано одно свойство А, то это множество разбивается на два класса: первый класс – объекты, обладающие свойством А, второй класс – объекты, не обладающие свойством А.

Если элементы множества обладают двумя независимыми свойствами, то все множество разбивается на 4 класса. Например, на множестве натуральных чисел заданы два свойства: «быть кратным 2» и «быть кратным 3». При помощи этих свойств в множестве N можно выделить два подмножества А и В. Эти множества пересекаются, но ни одно из них не является подмножеством другого (рис. 6). Тогда в первый класс войдут числа, кратные 2 и 3, во второй – кратные 2, но не кратные 3, в третий – кратные 3, но не кратные 2, в четвертый – не кратные 2 и не кратные 3.

П р и м е р 1. Пусть Х – множество четырехугольников, А, В и С – его подмножества. Можно ли говорить о разбиении множества Х на классы А, В и С, если:

а) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, противоположные стороны которых не параллельны;

б) А – множество параллелограммов, В – множество трапеций, С – множество четырехугольников, имеющих прямой угол?

Р е ш е н и е. а) Множества А, В и С попарно не пересекаются. Действительно, если у четырехугольника, противоположные стороны не параллельны, то он не может быть параллелограммом или трапецией. В параллелограмме противоположные стороны попарно параллельны, поэтому он не может принадлежать ни множеству В, ни множеству С. Наконец, в трапеции две противоположные стороны параллельны, а две другие не параллельны, поэтому трапеция не может принадлежать ни множеству А, ни множеству С. Объединение множеств А, В и С даст все множество четырехугольников. Условия классификации выполнены, множество всех четырехугольников можно разбить на параллелограммы, трапеции и четырехугольники, противоположные стороны которых не параллельны.

б) Множества А и В не пересекаются, но множества А и С имеют общие элементы, примером может служить прямоугольник, множества В и С тоже пересекаются: общим элементом является прямоугольная трапеция. Следовательно, нарушено первое условие классификации. Не выполняется и второе условие, так как некоторые четырехугольники не попадают ни в одно из подмножеств А, В или С, таким является четырехугольник с непараллельными сторонами и непрямыми углами. В этом случае множество Х на классы А, В и С не разбивается.

Задания для самостоятельной работы по теме:

Приведите примеры множеств А, В, С, если отношения между ними таковы:

2. Образуйте все подмножества множества букв в слове «крот». Сколько подмножеств получилось?

3 . Из множества N выделили два подмножества: А – подмножество натуральных чисел, кратных 3, и В – подмножество натуральных чисел, кратных 5. Постройте круги Эйлера для множеств N , A , B ; установите, на сколько попарно непересекающихся множеств произошло разбиение множества N ; укажите характеристические свойства этих множеств.

5. Имеется множество блоков, различающихся по цвету (красные, желтые, зеленые), форме (круглые, треугольные, прямоугольные), размеру (большие, маленькие). На сколько классов разбивается множество, если в нем выделены подмножества: А – круглые блоки, В – зеленые блоки, С – маленькие блоки? Сделайте диаграмму Эйлера и охарактеризуйте каждый класс.

6. Известно, что А – множество спортсменов класса, В – множество отличников класса. Сформулируйте условия, при которых: а) А ∩В=Ø

7. Пусть Х= < x N/ 1 x 15>. Задайте с помощью перечисления следующие его подмножества:

А – подмножество всех четных чисел;

В – подмножество всех нечетных чисел;

С – подмножество всех чисел, кратных 3;

D – подмножество всех чисел, являющихся квадратами;

Видео:Множество. Элементы множества. 5 класс.Скачать

Р множество трапеций q множество четырехугольников имеющих прямой угол

ПОМОГИТЕ РЕШИТЬ ПОЖАЛУЙСТА ЗАВТРА СДАВАТЬ!

Даны множества А,В,С. Изобразите отношения между ними. Укажите характеристическое свойство множеств АUВ, А∩С, АВ, А ∩ (ВС):

№ 11.
А – множество учащихся в школе;
В – множество девочек в школе;
С – множество учащихся третьих классов в этой школе.
№ 16
А – множество натуральных чисел;
В – множество натуральных чисел, кратных 5;
С – множество натуральных чисел, кратных 4.

№ 12
А – множество параллелограммов;
В – множество четырехугольников;
С – множество прямоугольников.
№ 17
А – множество прямоугольников;
В – множество четырехугольников;
С – множество квадратов.

№ 13
А – множество треугольников;
В – множество прямоугольных треугольников;
С – множество равнобедренных треугольников.
№ 18
А – множество трапеций;
В – множество параллелограммов;
С – множество четырехугольников, имеющих прямой угол.

№ 14
А – множество прямоугольных треугольников;
В – множество равносторонних треугольников;
С – множество равнобедренных треугольников.
№ 19
А – множество натуральных чисел, кратных 5;
В – множество натуральных чисел, кратных 3;
С – множество натуральных чисел, кратных 4.
№ 15
А – множество натуральных чисел, кратных 2;
В – множество натуральных чисел, кратных 3;
С – множество натуральных чисел, кратных 5.
№ 20
А – множество параллелограммов;
В – множество квадратов;
С – множество ромбов.

Видео:9 класс, 2 урок, Множества и операции над нимиСкачать

Правила построения отрицаний.

Задания на формирование умения строить отрицания составных высказываний

Типовые задания с решениями

Пример 1.Сформулируйте высказывания соответствующие формулама) ; б) ; в) , если А – «гремит гром»; В – «моросит дождь».

а) АÙВ – «Гремит гром и моросит дождь».

Т.к. º , «Гром не гремит или дождь не моросит»

б) АÚВ – «Гремит гром или моросит дождь».

Т.к. º Ù , — «Гром не гремит и дождь не моросит»

в) АÞВ — «Если гремит гром, то моросит дождь»

Т.к. º А Ù , — «Гремит гром и не моросит дождь».

Задания для самостоятельной работы (базовый уровень)

1. Сформулируйте отрицания следующих высказываний двумя способами.

а) 3 и 8 – однозначные числа.

б) Собака домашнее или дикое животное.

в) Картофель и тыква овощи.

г)Число 0,7 натуральное или целое.

д) Хотя бы одна из букв в слове «дом» гласная.

Определите значения истинности данных высказываний и их отрицаний.

2. Сформулируйте отрицания следующих высказываний, пользуясь формулами:

в) число 6 делится на 2 и на 3;

г) В романе «Война и мир» 70 или более страниц;

д) ель – лиственное или хвойное дерево;

е) ель — лиственное и хвойное дерево.

Задания для самостоятельной работы (повышенный уровень)

5. Задания на формирование умений:

устанавливать логическое следование и равносильность между предложениями,

формулировать обратную, противоположную и обратную противоположной теоремы,

устанавливать необходимые и достаточные условия.

Типовые задания с решениями

Пример 1.Доказать, что:

а) предикат Q(х) – «натуральное число х делится на 5 » логически следует из предиката Р(х) – «натуральное число х делится на 15»;

б) предикат Q(х) – «х – нечетное число» не является логическим следованием предиката Р(х) – «х – простое число»;

в) предикаты Q(х) – «противоположные стороны четырехугольника попарно параллельны» и Р(х) – «противоположные стороны четырехугольника попарно равны» равносильны.

а) Для доказательства логического следования Р(х) ÞQ(х) достаточно показать, что Т 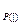Ì. Т Т.к. Т =, а Т =, то включение очевидноТ Ì. Т и требуемое утверждение доказано.

б) Для того доказать, что предикат Q(х) – «х – нечетное число» не является логическим следствием предиката Р(х) – «х – простое число», достаточно указать хотя бы один элемент, принадлежащий области ложности предиката Р(х) ÞQ(х), т.е. указать такое значение переменной х, при котором Р(х) обращается в истинное высказывание, а Q(х) – в ложное. В данном случае можно указать х=2, поскольку 2 число простое, но не является нечетным.

в) Для доказательства равносильности предикатов Р(х) и Q(х) достаточно показать, что Т = Т . По условию Т есть множество четырехугольников, противоположные стороны которых попарно параллельны, а Т — множество четырехугольников, противоположные стороны которых попарно равны. Поскольку в том и другом случае мы имеем дело с множеством параллелограммов, то и равносильность предикатов Р(х) и Q(х) можно считать доказанной.

Пример 2.Вместо многоточий вставить слова – «необходимо», «достаточно» или «необходимо и достаточно»:

а) для того, чтобы четырехугольник был ромбом, ……, чтобы его диагонали пересекались под прямым углом;

б) для того, чтобы сумма делилась на 19, ……, чтобы каждое слагаемое делилось на 19;

в) для того, чтобы треугольник был равнобедренным, ……, чтобы два внутренних угла его были равны.

а) Пусть Р(х) – «четырехугольник х — ромб», Q(х) – «диагонали четырехугольника х пересекаются под прямым углом». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): «Если четырехугольник ромб, то диагонали его пересекаются под прямым углом». Это высказывание истинно. Следовательно, Р(х)-достаточное условие для Q(х), а Q(х)-необходимое условие для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если диагонали четырехугольника пересекаются под прямым углом, то этот четырехугольник — ромб». Это высказывание ложно. Следовательно, условие Q(х) не является достаточным для Р(х), а Р(х) не является необходимым условием для Q(х).

Итак, Q(х)является необходимым условием для Р(х), но не является достаточным. Поэтому, вместо многоточия следует вставить слово «необходимо».

«Для того, чтобы четырехугольник был ромбом, необходимо, чтобы его диагонали пересекались под прямым углом».

б) Пусть Р(х) – «сумма х делится на 19», Q(х) – «каждое слагаемое суммы х делится на 19». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): « Если сумма чисел делится на 19, то каждое слагаемое этой суммы делится на 19».Последнее высказывание ложно. Следовательно, Р(х) не является условием достаточным для Q(х), а Q(х) не является необходимым для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если каждое слагаемое суммы делится на 19, то и вся сумма делится на 19».

Это высказывание истинно, а значит, Q(х) является условием, достаточным для Р(х), а Р(х) — необходимым для Q(х).

Итак, Q(х) является достаточным условием для Р(х), но не является необходимым. Поэтому вместо многоточия следует вставит слово «достаточно».

«Для того, чтобы сумма делилась на 19, достаточно, чтобы каждое слагаемое суммы делилось на 19».

в) Пусть Р(х) – «Треугольник х -равнобедренный», Q(х) –«Два внутренних угла треугольника х равны». Сформулируем утверждение в виде импликации («х)( Р(х) ÞQ(х)): «Если треугольник равнобедренный, то два внутренних угла его равны». Это утверждение является истинным, значит, Р(х) — достаточное условие для Q(х), а Q(х) – необходимое условие для Р(х).

Теперь сформулируем импликацию («х)( Q(х) Þ Р(х)): «Если внутренних угла треугольника, то этот треугольник равнобедренный». Это утверждение также является истинным, значит, Q(х) — достаточное условие для Р(х) , а Р(х)– необходимое условие для Q(х). Итак, Q(х) является необходимым и достаточным условием для Р(х), а значит, вместо многоточия следует вставит слова «необходимо и достаточно».

«Для того, чтобы треугольник был равнобедренным, необходимо и достаточно, чтобы два внутренних угла его были равны».

Пример 3.Выделить преамбулу, условие и заключение в теореме «В трапеции средняя линия параллельна основаниям». Сформулировать предложения: обратное, противоположное и обратное противоположному. Установит их истинность.

Решение. В теореме идет речь о множестве U — четырехугольников. Пуст х произвольно выбранный четырехугольник. Предикат Р(х) – « Четырехугольник х — трапеция» — условие теоремы, а предикат Q(х) – «Средняя линия четырехугольника х параллельна основаниям» — заключение теоремы. Тогда данную теорему можно символически записать в виде следующей импликации: («хÎ U)( Р(х) ÞQ(х)).

Здесь разъяснительная часть представлена квантором общности («хÎ U). В импликативной форме данную теорему можно сформулировать так; «Если четырехугольник – трапеция, то его средняя линия параллельна основаниям».

По определению, обратное предложение имеет логическую структуру («хÎ U)( Q(х) Þ Р(х)) и формулируется следующим образом: «Если средняя линия четырехугольника параллельна основаниям, то этот четырехугольник – трапеция». Последнее утверждение является ложным.

Предложение, противоположное данному имеет логическую структуру («хÎ U)( Þ и следующую формулировку: «Если четырехугольник – не является трапецией, то его средняя линия не параллельна основаниям» и также является ложным.

Предложение обратное противоположному, имеет логическую структуру («хÎU)( Þ и формулируется так: «Если средняя линия четырехугольника не параллельна основаниям, то этот четырехугольник – не трапеция».

Последнее утверждение является контрапозитивным прямой теореме и также истинно.

Задания для самостоятельной работы (базовый уровень)

1. На множестве Х= заданы предикаты: А(х): «Число х кратно 6» и В(х): «число х кратно 3».Укажите такие значения х, при которых:

а) предикаты А(х) и В(х) обращаются в истинные высказывания;

б) предикаты А(х) и В(х) обращаются в ложные высказывания.

2. На множестве Х= заданы предикаты: А(х): «Число х кратно 6» и В(х): «число х кратно 3». Сформулируйте импликацию А(х) ÞВ(х) и определите ее множество истинности. Можно ли утверждать что предикат В(х) следует из предиката А(х) на множестве Х?

3. На множестве Z – целых чисел задана импликация А(х) ÞВ(х): «Если число х больше 2, то оно положительное».

а) Найдите значение истинности этой импликации при х=3, х=1 и при х=-4.

б) Можно ли указать такое значение аÎХ, при котором А(а) истинно, а В(а) ложно?

в) Можно ли утверждать, что В(х) следует из А(х)?

г) Каково множество истинности импликации А(х) ÞВ(х)?

4. Докажите, что предикаты Р(х) – «Натуральное число х делится на 5» и Q(х) – «Десятичная запись натурального числа х оканчивается на 0 или 5» равносильны?

5. Докажите, что предикат Q(х) — «Натуральное число х делится на 13» логически следует из предиката Р(х) – «Натуральное число х делится на 26».

6.На множестве Х= заданы предикаты: А(х)- «(х-1)х=0»; В(х) – «х(х-1)(х-2)(х-3)=0.

а) Найдите их множество истинности и определите, в каком отношении эти множества находятся.

б) Верно ли, что А(х) логически следует из В(х)?

в) Можно ли утверждать, что А(х) – достаточное условие для В(х)? Если да, то сформулируйте предложение, используя термин «достаточно».

г) Можно ли утверждать, что В(х) – необходимое условие для А(х)? Если да, то сформулируйте предложение, используя термин «необходимо».

7. На множестве Z – целых чисел заданы предикаты: Д(х)-«х — делитель 12» и Е(х) – «х – делитель 36».

а) Докажите, что предикат Е(х) следует из предиката Д(х).

б) Сформулируйте предложение в виде «Если…., то»

в) Сформулируйте предложение с помощью слова «достаточно».

г) Сформулируйте предложение с помощью слова «необходимо».

8. Какие из следующих высказываний истинны:

а) Присутствие на всех занятиях по математике является достаточным условием для успешной сдачи экзамена по математике.

б) Наличие паспорта необходимо для приобретения билета на самолет.

в) Равенство числителя дроби нулю достаточно для равенства нулю всей дроби.

г) Достижение 18-летнего возраста необходимо для участия в выборах.

9. Сформулируйте следующие теоремы в импликативной форме, выделите разъяснительную часть, условие и заключение.

а) Диагонали прямоугольника равны.

б) Диагонали ромба взаимно-перпендикулярны.

в) Вертикальные углы равны.

г) В равнобедренном треугольнике углы при основании равны.

д) В правильный многоугольник можно вписать окружность.

е) Вписанный угол измеряется половиной дуги, на которую он опирается.

10. Для следующих теорем сформулируйте обратные, противоположные и обратные противоположным высказывания. Установите их истинность.

а) Если один из множителей делится на 23, то все произведение делится на 23. б) Если четырехугольник – ромб, то противоположные его углы равны.

в) Если число натуральное, то оно равно своему модулю.

г) Если треугольник правильный, то вокруг него можно описать окружность.

д) Если фигура квадрат, то она имеет центр симметрии.

е) Если дуги заключены между параллельными хордами, то они равны.

ж) Если фигура прямоугольник, то диагонали его точкой пересечения делятся пополам.

з) Если число представляется произведением трех последовательных натуральных чисел, то оно делится на 6.

и) Если дискриминант квадратного уравнения равен нулю, то это уравнение имеет два равных корня.

Задания для самостоятельной работы (повышенный уровень)

а) предикат А(х) обращаются в ложное высказывание, а предикат В(х) — в истинное высказывание;

б) предикат А(х) обращаются в истинное высказывание, а предикат В(х) — в ложное высказывание.

2. На множестве Х – учащихся школы заданы предикаты В(х): «Учащийся х — пионер» и А(х): «Учащийся х – член совета дружины».

а) Найти множество истинности предикатов А(х) и В(х).

б) Найдутся ли такие значения х, при которых А(х) обращается в истинное в высказывание, а В(х) – ложное.

в) Можно ли утверждать, что предикат В(х) следует из предиката А(х)?

г) Изобразите множества истинности предикатов А(х) и В(х) при помощи кругов Зйлера и укажите, в каком отношении эти множества находятся.

3.Докажите, что предикат D(х): «х =25», заданный на множестве R – действительных чисел, следует из предиката С(х): «х=5», заданного на том множестве.

Выясните, в каком отношении находятся множества истинности предикатов С(х) и D(х), изобразите их при помощи кругов Эйлера.

4.Предикаты А(х) и В(х) заданы на множестве Х. Множества их истинности обозначены Т и Т и соответственно и отношения между ними изображены на рисунке: