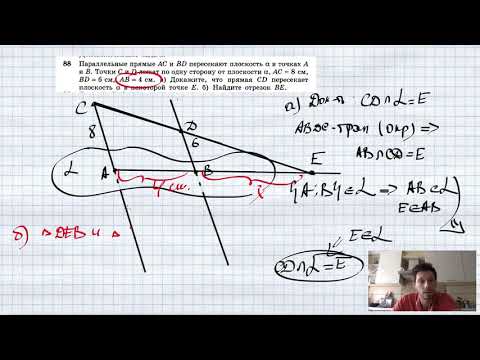
___ QF PQ _____ 6 NF _____ QF+4 10 Следовательно, см. Ответ, б) QF = см. 15 19 Точки А, В, С и D ве лежат в одной плоскости. Медианы треугольников АВС и CBD пересекаются соответственно в точках Mj и М^. Докажите, что отрезки AD и MjMg параллельны (задача 89 учебника). Доказательство. Середину отрезка ВС обозначим буквой Е. Отрезки АЕ и DE — ______________ треугольников _, поэтому точки Mj и —————и де- D и Mg лежат на лят их в отношении , считая от точки Е. Отсюда следует, что EM^ ЕА ЕМо ■ =—. Таким образом, стороны ЕМ^ и ЕМ^ треугольника ЕМ^М^ пропорциональны __________ а угол Е у этих треугольников — _______________ и, следовательно. Поэтому 20—————————— На рисунке ВС || DE, А i BCD. Докажите, что плоскости АВС и ADE пересекаются по прямой, параллельной прямым ВС и DE. Доказательство. Обозначим плоскости АВС и ADE через а и (3. Прямая DE не лежит в плоскости а, а прямая ВС не лежит __________, так как в противном случае эти плоскости совпали бы и тогда точка А лежала бы в плоскости BCD, что__________________________ точку А и поэтому, согласно_____ т. е. пересекаются по некоторой так как DE не лежит в __________ Плоскости аир имеют общую __, имеют________________, ____ а. По условию DE || ВС и _________, то по признаку ___________________ DE II а. Итак, плоскость Р проходит через прямую DE, параллельную плоскости ____, и пересекает ее по____________. Следовательно,———, а так как DE || ВС, то 16 Параллельность плоскостей Теорема (признак параллельности двух плоскостей). Если две пересекающиеся прямые одной плоскости___________________ ___________________ двум прямым другой плоскости, то эти плоскости Дано: прямые а и Ь, пересекающиеся в точке М, лежат в плоскости а, прямые Cj и bj лежат в плоскости Р, а || а^, Ъ II bj. Доказать: а II р. Доказательство. Заметим, что а II р, Ь II Р по признаку ______ плоскости а и Р не ______________ Теперь допустим, что __, а пересекаются по ____________________________ с. Тогда плоскость а проходит через прямую о, параллельную плоскости _____, и пересекает плоскость р по прямой с. Следовательно, а || с. Но плоскость а проходит и______________ следовательно, Ь || с. Таким образом, через точку М проходят две прямые ________, параллельные прямой_______Но это невозможно, так как по___________________________________________________ через точку М Значит, наше допущение неверно и а || р. Теорема доказана. 21 Две стороны треугольника параллельны плоскости а. Докажите, что и третья сторона параллельна плоскости а (задача 52 учебника). Доказательство. Пусть стороны АВ и АС треугольника АВС параллельны плоскости а. Докажем, что и третья сторона ВС параллельна плоскости а. Так как АВ || а, то, согласно заданию 10, в плоскости 17 а существует некоторая прямая AjBj II АВ. Аналогично существует прямая AjCj плоскости а, параллельная прямой АС. Итак, две пересекающиеся прямые АВ и АС плоскости АВС параллельны двум прямым AjBj и A,Cj плоскости а, следовательно, _________________ _____, эти плоскости , а потому прямая ВС __ плоскости а. 22 Точка F не лежит в плоскости треугольника MNP, точки Е, К W. Т лежат на отрезках FM, FN и FP, причем FE FK FT 2 FM FN FP 3 ■ а) Докажите, что плоскости ЕКТ и MNP параллельны. б) Найдите площадь треугольника MNP, если площадь треугольника ЕКТ равна 36 см^. Решение. а) Л EFK _______, так как ______ поэтому ЕК II____ и ЕК = Аналогично Л KFT _________, так как , поэтому КТ и КТ = Итак, пересекающиеся прямые ЕК и КТ плоскости ЕКТ соответственно __________________________________________ плоскости MNP, следовательно, эти плоскости_____________ б) А ЕКТ _______, так как —————————— подобия к равен S. Поэтому S, ‘MNP , и коэффициент . = —, откуда ‘MNP Ответ, б) 18 23 На рисунке параллельные плоскости аир пересечены прямыми MN и MF, Pj, Pg и Qj, Qg — точки пересечения прямых с плоскостями а и р. Найдите PjPg. если MPj : MQ^ = 3 : 4 и = 72 см. Ре ш е н и е. 1) Пересекающиеся прямые MN и MF задают некоторую______________ у. и Pj — общие точки плоскостей а и у, поэтому прямая PjPa — ________________ М , аналогично Qj и — поэтому прямая QjQg —_______________ Итак, параллельные плоскости а и Р пересечены плоскостью у, поэтому, согласно _____________________________ пересечения р.р, II—— линии их _____ , т. е. 2) ДР^МРз
_ MP^:MQ^=P^P^: Ответ. _______ так как Р Р = ^ 2 — следовательно. § 4 24 Тетраэдр и параллелепипед в тетраэдре MNPQ ребро MN = = 3-/2см, NP = NQ = 7 см, PQ = 8 см, ZL MNP = ZL MNQ = 45°. Найдите площадь грани MPQ. Решение. 1) AMNP = AMNQ, так как , поэтому МР = М 2) По теореме косинусов для треугольника MNP имеем: МР^ = , откуда МР =___см. 3) Д MPQ равнобедренный, так как________ сота ME является_______________, т. е. РЕ = . угольном треугольнике МЕР гипотенуза _ , а потому его выем. Итак, в прямо-_________, катет 4) = — Ответ. ___ , следовательно, ME = _ 1 2 см. см^ = см’^ 25—————————- Через середины ребер АВ и ВС тетраэдра SABC проведена плоскость, параллельная ребру SB. Докажите, что эта плоскость пересекает грани SAB и SBC по параллельным прямым (задача 69 учебника). Доказательство. Пусть MNQ — плоскость, проходящая через середины М и N ребер АВ и ВС и параллельная ребру SB. Плоскость SAB проходит через прямую SB, параллельную плоскости _____, и пересекает ее по прямой MQ, поэтому MQ ______. Аналогично плоскость SBC проходит и пересекает MQ II SB и __ поэтому __, поэтому _________. Итак, , что и требовалось доказать. 26 в тетраэдре SABC точки М и К лежат на ребрах SB и ВС, а точка Т — на продолжении ребра ВС. Постройте: а) точку пересечения прямых МК и SC; б) точку пересечения прямой ТМ и плоскости ASC. Решение. а) Прямая МК лежит в плоскости SBC, так как точки ___________________________________________, причем на рисунке прямые МК и SC не параллельны, поэтому прямая МК пересекает 20 прямую sc в некоторой точке _________ . Итак, _____ — точка пересечения пря- мых МК и SC. б) Прямая ТМ лежит в плоскости BSC, так как точки _______________________ __________________На рисунке прямые ТМ и SC не параллельны, поэтому прямая ТМ пересекает прямую SC в некоторой точке_____, а так как прямая SC лежит в плоскости ASC, то и точка _____е ASC. Следовательно, прямая ТМ пересекает плоскость ASC в точке ____ 27 Точки М и N расположены на гранях ADB и ADC тетраэдра DABC. Постройте точку пересечения прямой MN с плоскостью АВС. Решение. Поскольку точки D и М лежат в плоскости ADB, то прямая DM ____________________________ _________________ и пересекает ребро Аналогично прямая DN пересекает _________Точки F к К лежат в плоскости DMN, а потому и _____________ ______________________ лежит в ————————-Так как на рисунке прямая MN не параллельна прямой FK, то прямая MN пересекает прямую________в некото- рой точке Т. Прямая FK лежит в плоскости АВС, поэтому точка ————— и, значит, прямая MN пересекает плоскость ________ в точке____ 28 Точки Aw. В расположены на гранях SMN и SNP тетраэдра SMNP. Постройте точку пересечения прямой АВ с плоскостью SMP. 21 Решение. Поскольку точки N и А лежат в плоскости SMN, то прямая NA и пересекает _________________________ Аналогично прямая NB лежат в плоскости __________лежит в Итак, точки _____ ANB, а потому и . этой плоскости. На рисунке прямые АВ и FK не параллельны, следовательно, прямая АВ пересекает прямую________ в некоторой точке_____, и так как прямая FK лежит в плоскости SMP, то и точка ___________, а значит, прямая АВ пересекает плоскость в точке 29 На ребрах АС и ВС тетраэдра SABC отмечены точки Р и К, а на продолжении ребра SC — точка Т. Постройте сечение тетраэдра SABC плоскостью РКТ. Решение. Поскольку точки Т н Р лежат в плоскости________, то прямая ТР лежит _______________ и пересекает ребро ______ ____ в некоторой ____________. Аналогично прямая ТК лежит в плоскости________и пересекает ребро ——————————- Следовательно, сечением тетраэдра SABC плоскостью РКТ является ______________ Проведите указанные прямые и постройте искомое сечение. 30 в тетраэдре SABC точки D, Е и F являются серединами ребер SA, АВ и ВС, АС = 32 см, SB = 40 см, угол между прямыми АС и SB равен 90°. а) Докажите, что плоскость DEF проходит через середину Р ребра SC. б) Найдите площадь четырехугольника DEFP. 22 Решение. а) EF — средняя линия треугольника , поэтому EF II______, и по признаку _________________________EF II ASC. Плоскости ASC и DEF имеют общую точку D и потому, согласно _____________, имеют общую прямую, проходящую через точку___Обозначим эту прямую буквой а. Так как плоскость DEF проходит через прямую EF, параллельную плоскости______, и пересекает эту плоскость по прямой ___, то о II_____. Мы получили, что АС || EF и а || EF, откуда следует по ____________________________________________________, что а II АС. __, прямая а. Рассмотрим А ASC. Точка D — середина стороны , следовательно, прямая а _____Тем самым мы дока- проходящая через точку D, параллельна__ пересекает сторону SC в точке Р — середине зал и, что плоскость DEF проходит через середину Р ребра_ б) Четырехугольник DEFP — параллелограмм, так как ——————————-, причем EF =__________, а DE = = _________________, так как DE — средняя ______________________ Рассмотрим угол DEF. Его стороны ED и EF соответственно параллельны прямым BS и АС, угол между которыми по условию равен 90°. Поэтому и ZL DEF =_______, и, значит, параллелограмм DEFP является ^DEFP
Ответ, б) . 31——— см“ На рисунке изображен тетраэдр KLMN. а) Постройте сечение этого тетраэдра плоскостью, проходящей через ребро KL и середину А ребра MN. б) Докажите, что плоскость, проходящая через середины Е, О я F отрезков LM, МА и МК, параллельна плоскости LKA. Найдите площадь треугольника EOF, если площадь треугольника LKA равна 24 см^ (задача 75 учебника). 23 Решение. а) Так как точки ЬиА принадлежат секущей плоскости и грани_______тетра- эдра, то секущая плоскость пересекается с этой гранью по______________Анало- гично секущая плоскость пересекается с гранью KMN по________________Следовательно, _________________________— искомое сечение. б) Рассмотрим плоскости EFO и LKA. EF II LK и ЕО II LA, так как _______ К Итак, две пересекающиеся прямые плоскости EFO соответственно параллельны двум прямым плоскости _________, поэтому, согласно плоскости EFO и________________ EOF и LAX подобны, так как . Треугольники причем коэффициент подобия равен____, так как_______________По теореме об отношении площадей подобных треугольников имеем: _, откуда =———————————=————— CM^ = С «с = ^EOF • ^^LAK Ответ, б) 32 Докажите, что отрезки, соединяющие середины противоположных ребер тетраэдра, пересекаются и точкой пересечения делятся пополам (задача 101 учебника). Доказательство. 1) Пусть М, N, Р к Q — середины ребер DA, DC, ВС и АВ тетраэдра DABC. Тогда отрезки MQ и NP — средние и поэтому MQ II _ NP II____и NP = и MQ =_______, .. Следовательно, D 24 MQ и MQ =______, и, значит, четырехугольник MNPQ — _________________________, а отрезки МР и NQ — его ____________________. Отсюда следует, что отрезки МР и NQ, соединяющие середины противоположных ребер ______ и ——, —- и _____тетраэдра DABC, пересекаются и точкой пересечения О делятся пополам. 2) Теперь рассмотрим отрезки NQ и EF, соединяющие середины противоположных ребер CD и АВ, BD и АС. Как и в п. 1, можно доказать, что четырехугольник ENFQ — ————————— и, следовательно, его диагонали EF и NQ пересекаются ____________________________, т. е. в точке__ Итак, точка О является серединой отрезков МР, NQ и EF, что и требовалось доказать. 33 На ребрах DD^ и CCj параллелепипеда ABCDA^BjC^D^ отмечены точки Р и F. Постройте точку пересечения: а) прямой PF с плоскостью АВС б) прямой BF с плоскостью AjBjCj. Решение. а) Поскольку точки Р и F лежат в плоскости Z)Z)jCj, то прямая PF ■ — > и так как на рисунке прямые PF и DC не параллельны, то прямая PF пересекает прямую ______, а значит, и ________________________ в некоторой б) Поскольку точки В и F лежат в ВС и BjCj также лежат в Ог Pi F С , то прямая _ . Прямые _________________, причем эти прямые и прямая BF пересекает прямую _____ в точке ___. Поэтому прямая BF А так как прямая В^С^ лежит в плоскости А^В^С^, то и точка ____ле- жит в этой плоскости. Следовательно, прямая BF пересекает плоскость AjBjCj в точке___ 25 34 в параллелепипеде ABCDA^B^C^D^ точка F лежит на ребре AD, Т — внутренняя точка грани CC^D^D. а) Через точку Т проведите плоскость а, параллельную плоскости B^BF. б) Постройте линию пересечения плоскости а с плоскостью AA^D^. Вг Решение, а) Проведем РТ и PN Прямые РТ и PN задают Cl б) Прямая NP — линия пересечения плоскостей а и ______, причем прямая NP пересекает прямую AD в некоторой точке Q, и так как прямая AD лежит в плоскости AAjDj, то точка Q является общей точкой двух плоскостей а и AA^D^. Следовательно, эти плоскости пересекаются по прямой QQj, проходящей через точку Q и параллельной прямой____ Итак, QQj — линия пересечения плоскостей____и_________ 35 ABCDA^B^C^D^ Cl Вг В параллелепипеде точки F, Р и Е лежат на ребрах AD, CC^ и jD£)j. Постройте сечение параллелепипеда плоскостью FPE. Решение. Грани ADD^A^ и CDD^C^ пересекаются с плоскостью FPE по отрезкам _____ и ______. Плоскость FPE пересекает грань СС^В^В по отрезку РК прямой, проходящей через точку Р и параллельной прямой______грани AA^DJ), так как грани _______________________ параллельны. На рисунке прямая РК пересекает ребро ВВ^ в некоторой точке __. Аналогично плоскость FPE пересекает грань АА^В^В по отрезку прямой, проходящей через точку____и параллельной прямой_______грани ———, а ребро АВ в некоторой ___________ Итак, пятиугольник FEP. — искомое сечение. 26 36 в параллелепипеде ABCDA^B^C^D^ на ребрах АВ и ВС отмечены точки М к N. а) Постройте сечение параллелепипеда плоскостью D^MN. б) Постройте линию пересечения секущей плоскости и плоскости BD^By Решение. а) Пусть прямая MN пересекает продолжения ребер AD и DC в точках Р и Q. Тогда прямые PD^ и QD^ пересекают ребра в некоторых точках____________ Итак, искомое сечение —_________ б) Плоскости D^MN и BDD^ имеют общую точку аксиоме______пересекаются._______________________ , а потому по 37 а) Постройте сечение параллелепипеда ABCDAjBjCjDj плоскостью AEF, где точка Е принадлежит ребру ВС, а F — внутренняя точка грани DCC^Dy б) Укажите точку пересечения диагонали DBj параллелепипеда с секущей плоскостью. Решение. а) Пусть прямая АЕ пересекает продолжение ребра____в некоторой точке___, тогда прямая ____ лежит в плоскости ______и пересекает ребра _ Итак, искомое сечение — в некоторых точках б) Пусть прямые BD и АЕ пересекаются в некоторой точке Р. Тогда прямые______и______лежат в плоскости DBB^ и_____________________ 27 38—————————— а) Постройте сечение параллелепипеда ABCjDAjBjCjDj плоскостью, проходящей через точки Р, F и М — середины ребер AAj, и DC. б) Укажите точку пересечения диагонали BD^ с секущей плоскостью. Решение. а) Пусть прямая FP пересекает С, Итак, искомое сечение б)——————— 39 Точка М лежит на ребре ВС параллелепипеда ABCDA^BjC^D^. Постройте сечение этого параллелепипеда плоскостью, проходящей через точку М параллельно плоскости BDCj (задача 115 учебника). Решение. В плоскости BBjCj через точку М проведем прямую ME, параллельную _____, Е € CCj, а в плоскости АВС через__________проведем прямую, _____________и пересекающую ______ в точке F. Плоскость МЕР параллельна плоскости___________ по ——————————— Cl D, Следовательно, искомое сечение — треугольник МЕР. 28 40——————————————————— Отрежьте по штриховой линии часть листа с разверткой и наклейте ее на тонкий картон или плотную бумагу. Вырежите развертку, аккуратно согните по линиям и склейте. Вырежите и склейте развертку, изображенную на следующей странице. Получится две части тетраэдра, рассеченного плоскостью. Сложите из них тетраэдр с сечением ABCD. 29 i Y-‘ -‘•ч’ f . .• :v. ..
i. >J? ;■ •v:. Я .4. *’.;::тог, M» txo’ rrif-, н:-ниу. ■ . t ^ У’ U-. ,i? r “ 1 .’iO 1* N-i I’-rt. or ‘ C HJ #i J к V • I • i > ;i . »i,’ 4 ‘Г t ‘.lil’ -‘i :!*> • f « .-X 31 »V ‘Ч ► V г, л / •л 41——————————————————— Отрежьте по штриховой линии часть листа с разверткой и наклейте ее на тонкий картон или плотную бумагу. Вырежите развертку, аккуратно согните по линиям и склейте. Вырежите и склейте развертку, изображенную на следующей странице. Получится две части параллелепипеда, рассеченного плоскостью. Сложите из них параллелепипед с сечением ABCDE. t 33 Г! ■ > ; «ч л, ■ -■ ‘‘J t..-. I м» ‘ -iliij ’ ^ ‘Т Ч P- f ‘ HO ‘ f* ‘ 1 •. ■ ‘‘•If., v; ■ ■ иД.’я ■ ■•.. ^ -f ?’ N I . ‘И;Н1 . ‘О I I Ч . I J 35 ;■ ч -vt» . . -‘ ч. Глава II Перпендикулярность прямых и плоскостей Перпендикулярность прямой и плоскости 42 в тетраэдре МАВС ребра МА и ВС перпендикулярны, Р — точка ребра АВ, причем АР : АВ = 2:3, Q — точка ребра АС и AQ: QC = 2:1. Докажите, что МА J- PQ. Доказательство. AAPQo^ ААВС, так как ________________________ _________________________ Поэтому PQ II __, и угол между прямыми МА и PQ______________, т. е. МА J__ М С Теорема (признак перпендикулярности прямой и плоскости) Если прямая перпендикулярна к двум ___________________ прямым, ________________________________________________, то она___________________________________________________ Дано: а Ар, а Aq, прямые р н q лежат в плоскости а и пересекаются в точке О (рис. а). Доказать: а А а. Доказательство. Для доказательства перпендикулярности прямой а и плоскости а надо доказать, что а А т, где т — Рассмотрим два случая. 1) Пусть О € а, I \ т и О € I, прямая п пересекает прямые р, q и I в точках Р, Q, L, ОА = ОВ (рис. б). Так как прямые р и q — серединные 37 и AQ =_____, и, следовательно, Л APQ = Л BPQ по ________________ ___________________. Поэтому А APQ = ___________. Далее Л APL = = Л BPL по , поэтому AL = , , а это означает, что AABL — и его медиана LO является ________ Так как 1\ т и I ± а, то по лемме , т. е. LO±AB или ZJ__ т . Таким образом, прямая а перпендикулярна к любой прямой плоскости а, а это означает, что 2) Пусть О i а (рис. в). Проведем а, || а, Ое a^. Тогда р k Oj JL g по лемме __________________________________________ и. следовательно, ± а согласно _____________________________________. Итак, одна из параллельных прямых а и перпендикулярна ________________________, поэтому и вторая прямая________________ ___________________________________, т. е. о J__Теорема доказана. 43 Через точку О пересечения диагоналей ромба ABCD проведена прямая ОМ, перпендикулярная к плоскости ромба, причем ОМ = 6 см, АС= 16 см, BD= 4л/з см. Найдите: а) расстояние от точки М до вершин ромба; б) расстояние от точки М до стороны DC. 38 Решение, а)ЧетырехугольникABCD — ромб, а отрезки АС и BD — его диагонали, пересекающиеся в точке О, поэтому ОА =_____, ОВ =______. Так как МО ± i-АБС, то МО А_______и МО А_______. В треугольниках АМС и BMD медиана МО является и _____________, поэтому эти треугольники ________________________, т. е.________________________________ Из прямоугольного треугольника АОМ с катетами 6 см и 8 см имеем: МА —_____ Из прямоугольного треугольника ВОМ находим: МВ =______________см. Итак, МА = МС =________, МВ = MD =________ б) В треугольнике ВМС проведем МР1. ВС и рассмотрим плоскость МОР. Прямая ВС перпендикулярна к двум пересекающимся прямым______ и —- этой плоскости, следовательно, по ________________________ ВС L. _____________________________________________, а потому перпендикулярна к любой прямой, лежащей в этой плоскости, в частности ВС А- ОР. АСОВ прямоугольный, так как____, ^„ СО -OD ОР — его высота, поэтому ОР =——= ____________ = ________ DC Ответ, а)_______; б)________ 44—————————————————— На рисунке AF±ABC, ВМ ±АВС. Докажите, что линия пересечения плоскостей AFC и ВМС параллельна прямым AF и ВМ. Доказательство. Так как AF1ABC и ВМА.АВС, то AF ||__, и, следовательно, AF || ВМС по _______________________ Плоскость AFC проходит через прямую AF, параллельную плоскости ______, и пересекает эту плоскость. Следовательно, линия пересечения плоскостей ____________ параллельна прямой ____. А так как AF || ВМ, то по _________________________________ прямая ВМ также параллельна 39 м 45—————————- Четырехугольник ABCD — квадрат, О — точка пересечения его диагоналей, ОМ L АВС. Докажите, что: а) BD LMAvi BD I МС б) АС 1 МВ и АС ± MD. Доказательство. Четырехугольник ABCD — квадрат, поэтому АС J_____По условию МО ± АВС, следовательно, МО J__и МО J_____ а) Рассмотрим плоскость АМС. Прямая BD перпендикулярна к двум пересекающимся прямым ___________этой плоскости, следовательно, по BD J______, а потому прямая BD перпендикулярна к любой прямой, лежащей в этой плоскости, в частности BD J____и BD J______ б) Рассмотрим плоскость BMD. 46 в тетраэдре МАВС АВ = АС, МВ = МС. Докажите, что ВС J_ AM. Доказательство. По условию треугольники ВАС и ВМС —______________ _____с общим_____________________, поэтому их медианы АН и МН, проведенные к____________________, являются ___________________, т. е. АН J__и Рассмотрим плоскость АМН. Так как ВС J_ АН и ВС J_______, то по М ВС А-АМН, а потому прямая ВС перпендикулярна к любой ___________________________________________________ в частности ВС± 40 47 Дан куб ABCDA^B^CJ)^. Докажите, что диагональ куба B^D перпендикулярна к диагонали АС его основания. Доказательство. Так как грани АА^В^В и ВВ^С^С — квадраты, то В^В ± ВА и BjB ± ВС. Следовательно, BjB J. АВС по__________________ ______. Рассмотрим плоскость Поскольку АС ± BD, так как B^BD. так как _ , и АС J- В,В, , то АС J______ В. Cl по а потому АС ± 48 Докажите, что через каждую из двух взаимно перпендикулярных скрещивающихся прямых проходит плоскость, перпендикулярная к другой прямой (задача 137 учебника). Доказательство. Пусть а и Ь — скрещивающиеся прямые, причем а ±Ь. Докажем, что через прямую Ь проходит плоскость, перпендикулярная к прямой а. Возьмем на прямой Ь какую-нибудь точку М и проведем через нее прямую а^, параллельную прямой а. Так как Cj || а и а ±Ь, то Oj J__Пересекающиеся пря- мые a^ и Ь определяют некоторую плоскость а. Пусть прямая с проходит через точку М и перпендикулярна к плоскости а. Тогда с ± 6 и с J_. Пересекающиеся прямые & и с определяют некоторую плоскость р. Поскольку а^±Ь и Oj ± с, то Oj J_по _______________________________ а так как а Oj, то а ± . Итак, плоскость р проходит через прямую Ъ и перпендикулярна к _____________Аналогично доказывается, что через прямую а про- ходит 41 § Перпендикуляр и наклонные. Угол между прямой и плоскостью 49 м Из точки М к плоскости а проведены перпендикуляр МО и две наклонные МА и МВ, которые образуют со своими проекциями на эту плоскость МАО = 45°, Z МВО = 30°, угол между наклонными равен 90°. Найдите расстояние между основаниями наклонных, если проекция наклонной МА равна >/з см. Решение. МО ± а, поэтому МО А______и МО А______ААМО прямоугольный и равнобедренный: Z. О = ___, /-А = А____ = _____, АО = _______, следовательно, МО =_________, AM =_______. А ВМО прямоугольный: АО =_______, А В =_____, МО =______, поэтому МВ = 2_____=_____см. ААМВ прямоугольный: AM = _______, поэтому АВ =________ Ответ. ____см. 50————————— АМ = ВМ = см. Концы отрезка отстоят от плоскости а на расстояниях 1 см и 4 см. Найдите расстояние от середины отрезка до плоскости а (задача 142 учебника). Решение. Рассмотрим два случая: 1) концы отрезка находятся по одну сторону от плоскости а; 2) концы отрезка находятся по разные стороны от плоскости а. 1) Пусть отрезок АВ расположен по одну сторону от плоскости а (см. рис. а), AAj ± а, АА^ = 1 см, ВВ^ ± а, ВВ^ = 4 см. Так как АА^ J_ а и BBj ± а, то AAj II____, и поэтому четырехугольник А^АВВ^ — _____________Проведем в ней среднюю линию РР^, тогда РР^ II__, РР, II_____, и так как АА^ ± а, то и РР^ J_______. Следовательно, длина отрезка РР^ и есть искомое расстояние от середины отрезка 1 АВ до плоскости а, PPj = -_________________ = ___________________ = =_____см. 42 а) 2) Пусть концы отрезка АВ расположены по разные стороны от плоскости а (см. рис. б) и пусть АА^ и ВВ^ — перпендикуляры к плоскости а, AAj = 1 см, BBj = 4 см. Так как АА^ J_ а и BBj ± а, то АА^ ||_, и прямые AAj, BBj, А^В^ лежат в одной___________. Проведем через точку Р — середину отрезка АВ — прямую, параллельную В^В. Тогда по__________________________________________точки Р^и F пересе- чения этой прямой с прямыми AjBj и AjB будут серединами отрезков _____и________, а отрезки P^F и PF — средними_________________ ____________________________________________= — _________________= см. Ответ. см или см. 51 Докажите, что концы данного отрезка находятся на одинаковом расстоянии от любой плоскости, проходящей через его середину. Доказательство. Пусть плоскость а проходит через середину М отрезка АВ, АА, J. а, BBj ± а. Тогда AM = МВ, А АМА^ = А ВМВ, и_____ 52 Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см. Найдите расстояние от точки М до плоскости АВС, если АВ = 6 см (задача 143 учебника). Решение. Пусть МО — перпендикуляр к плоскости АВС, тогда расстояние от точки М до плоскости а равно ____. Так как МО _L а, то МО J_ ОА, МО 1______, МО ±________Л АОМ = . м по точка О равноудалена от , следовательно, ОА = ОВ = ОС, т. е. и, значит, является центром этого треугольника. Поэтому АО = _______= _____________=______ (см), и из прямоугольного треугольника АМО находим: МО =_______________= __________(см) = ___см. Ответ. см. 53 Через вершину А прямоугольного треугольника АВС с прямым углом С проведена прямая AD, перпендикулярная к плоскости треугольника. Докажите, что треугольник CBD прямоугольный (задача 145 а учебника). Доказательство. Из точки D к плоскости АВС проведены перпендикуляр ____ и наклонная_____Прямая ВС лежит в плоскости АВС и перпендикулярна к проекции____наклонной___ согласно _________________________ В на эту плоскость, поэтому. ВС J- DC , т. е. треугольник CBD 44 54 Дан параллелепипед ABCDA^B основанием которого является ромб ABCD, а боковое ребро перпендикулярно к плоскости основания. Докажите, что диагональ B^D параллелепипеда перпендикулярна к диагонали АС его основания. Доказательство. ВВ^1.АВС _____________, диагональ B^D — наклонная к плоскости АВС, BD — проекция _________ ____________________, диагональ АС В, Сг лежит в плоскости АВС, АС _L BD, так как Следовательно, согласно теореме АС J-_____ 55 м Сторона ромба ABCD равна 12 см, А А = 30°, AM J_ ABC, AM = 6 см. Найдите расстояние от точки М до прямой CD. Решение. Из вершины А ромба ABCD проведем отрезок АН ± DC. Так как А ADC =______— тупой, то основа- ние Н перпендикуляра АН лежит на продолжении луча ____. Таким обра- зом, из точки М к плоскости АВС проведены перпендикуляр МА и наклонная МН, при этом прямая CD плоскости _______ перпендикулярна к проекции _____ наклонной ____. Поэтому, согласно __________________________ ___________________________, CD J__. Итак, длина перпендикуляра МН и есть расстояние от точки_до прямой_____ Л AHD _____________________, А ADH =_______, AD =________, поэтому АН =__см. Л МАН ____________________________ ______________и AM =_______, АН =__см, поэтому МН =. так как ____см. Ответ. см. 45 56 —————————— Через точку А, удаленную от плоскости а на расстояние л/з см, проведена прямая, пересекающая плоскость а в точке В. Найдите угол между прямой АВ и плоскостью а, если АВ — 2 см. Решение. Пусть отрезок АО — перпендикуляр к плоскости а. Тогда АО = =_________, прямая ОВ — проекция ————————————> а угол между прямой АВ и плоскостью а равен А______Из прямоугольного треугольника АОВ находим: sinZ.ABO =_ /1 ABO =___ Ответ._____ 57 —————————— следовательно. В прямоугольном треугольнике АВС АС = 90°, АВ= см. Точка Р не лежит в плоскости АВС и удалена от каждой вершины треугольника на расстояние 4^Js см. Найдите угол между прямой PC и плоскостью АВС. Решение. Пусть РО — перпендикуляр к плоскости АВС. Поскольку отрезки РА, РВ и PC — равные наклонные, проведенные из ___________ к _ проекции тоже _________, т. е. ОА = . О — центр окружности, _____________ то их , а потому точка . Так как АВ = . Следовательно, точка О — середина 1 ‘ __=______см. Искомый угол ф между прямой между ———————— т. е. ф = Z.. PC =______ __, то СО = — 2 И плоскостью есть угол _____Л РОС прямоугольный, так как , СО =______см, поэтому cos ф =___ . Отсюда получаем, что ф = Ответ. 46 Двугранный угол. Перпендикулярность плоскостей 58 к плоскости равнобедренного прямоугольного треугольника АВС с гипотенузой АВ = 12-Тз см проведен перпендикуляр DC, равный 18 см. Найдите угол между плоскостями DAB и САВ. Решение. Треугольники АВС и ADB равнобедренные: А АВС___________ __________, а в А ADB DA =_____, так D как эти стороны — ________________ . Поэтому медианы CF и DF этих треугольников, проведенные из вершин С и I) к общему основанию ___________, являются ______________________________________________________, и, следовательно, А DFC — линейный угол ______________________________________, а значит, угол между плоско- стями DAB и САВ равен А CF = -2 А DCF прямоугольный, DC = см и поэтому tg А DFC = , откуда А DFC = Ответ. 59—- Катет АС прямоугольного треугольника АВС с прямым углом С лежит в плоскости а, а угол между плоскостями а и АВС равен 60°. Найдите расстояние от точки В до плоскости а, если АС = 5 см, АВ = 13 см (задача 172 учебника). Решение. Проведем перпендикуляр ВО к плоскости а. Отрезок ВС — наклонная к_______________________, отрезок ОС — проекция наклонной_____ на________________, а прямая АС, ле- жащая в плоскости а, перпендикулярна к наклонной ВС. Следовательно, согласно ————————————————- , 47 АС -L ОС. Таким образом, Z. ВСО — линейный угол двугранного угла между плоскостями а и АВС, и, значит, А ВСО =____ Д АВС прямоугольный: АС= _______, АС = _______, АВ = _________, поэтому ВС —________ А ВСО прямоугольный: АО =_______, А ВСО =______, ВС =_________, следовательно, ВО = ___________см = __________см = _______см. Ответ. _______см. 60 Через сторону AD ромба ABCD проведена плоскость ADM так, что двугранный угол BADM равен 60°. Найдите сторону ромба, если А BAD = 45° и расстояние от точки В до плоскости ADM равно 4л/з (задача 176 учебника). Решение. Проведем перпендикуляр ВР к плоскости ADM. Искомое расстояние от точки В до плоскости ADM равно ВР. Проведем высоту ромба BE. Тогда получим, что из точки В к плоскости ADM проведены перпендикуляр _______ и наклонная _______________________ Следовательно, отрезок РЕ — проекция ___________________на____________ Прямая AD, лежащая в плоскости ADM, перпендикулярна к наклонной BE, а потому, согласно _______________________________ __________________________, AD J______, и А ВЕР — линейный ________________________________, т. е. А ВЕР = ____ угол Л ВРЕ прямоугольный, так как __________ А ВЕР =_____, ВР =_______, поэтому BE =. , причем А ВАЕ прямоугольный: АЕ = . следовательно, АВ — ________ Ответ._________ , АА = , BE = 48 61 Найдите измерения прямоугольного параллелепипеда ABCDA^Bfi^D^, если его диагональ BD^ = 24 см и составляет с плоскостью грани DAA^ угол в 45°, а с ребром DDj — угол в 60°. Решение. Все грани прямоугольного параллелепипеда — _________________, поэтому ВА J_____, ВА J_____, и, сле- довательно, ВА _L DAA^. Прямая BD^ пересекает плоскость DAA^ в точке__, а прямая ADj — проекция ______ на эту плоскость, поэтому /LAD^B — это угол между диагональю ______ и __________ Z ADjB =. АА =_____ В ___________________По условию . Из прямоугольного треугольника AD^B, в котором D^B = . и находим: AB=AD = ром А D =. ем: D,D = -‘ 2 /!£) = _ , ADj = . см. Из прямоугольного треугольника BD^D, в кото- ____, Z BD^D =_____ по условию, получа- _ см. Из треугольника AD^D, в котором __, DDj =_______, находим: AD =_____см. BD,= Ответ. 62 Докажите, что любая точка прямой, которая проходит через центр окружности, описанной около многоугольника, и перпендикулярна к плоскости многоугольника, равноудалена от вершин этого многоугольника (задача 200 учебника). Доказательство. Пусть прямая а проходит через центр О окружности, описанной около многоугольника AjAg. A^, и перпендикулярна к плоскости а этого многоугольника. Ясно, что точка О равноудалена от вершин многоугольника, так как является центром описанной около него окружности: ОА^ = ОА^ = . = ОА^. Пусть М — произвольная точка прямой а, отличная от точки О. Тогда 49 МО — перпендикуляр, МА,, МА^, МА^ проведенные из точки ____ к __________ OAg, — проекции наклонных на как проекции равны, то равны и_____ , а ОА,, ____Так т. е. . Таким образом, любая точка прямой а равноудалена от 63 в треугольнике АВС АВ = 13 см, ВС = 14 см, АС =15 см. Точка М удалена от прямых АВ, ВС и АС на 5 см. Найдите расстояние от точки М до плоскости АВС, если известно, что ее проекция на эту плоскость лежит внутри треугольника. Решение. Пусть МО — перпендикуляр к плоскости АВС, а MN, МР и MQ — перпендикуляры к прямым АВ, ВС и АС. Требуется найти МО. По теореме,____________________________ имеем: АВ ± ON, ВС _L , и АС ± . Итак, из точ- ки М проведены к плоскости АВС перпендикуляр МО и наклонные MN, МР и MQ. По условию расстояния от точки М до прямых АВ, ВС и АС равны, т. е. равны наклонные__, _____и_______Следовательно, потому равны и их проекции на эту плоскость: _ Таким образом, точка О лежит внутри треугольника АВС и равноудалена от_______________, поэтому она является _________________ Радиус ON этой окружности найдем, используя формулу S=pr, где S — площадь треугольника АВС, р — его ________________________, р =_______, г = ON. По формуле Герона S = ____________________= см^, следовательно, г = (см) = . см. Итак, N0 =____см. Треугольник MON _______________ и потому МО J______Так как MN = угольника MON находим: МО =_______ Ответ._____ см. поскольку_______LABC, , ON =_______, то из тре- =____см. 50 Глава III Многогранники Понятие многогранника. Призма 64 Сколько граней, ребер, вершин и диагоналей у каждого из изображенных на рисунке многогранников? D N а) Тетраэдр б) Параллелепипед в) Октаэдр Решение. а) Тетраэдр DABC составлен из _ ребер и ______ вершины. Диагональю многогранника называется граней. Он имеет , соединяющий две , не принадлежащие . У тетраэдра любые две вершины одной грани, следовательно, у него б) ————————— диагоналей. ABCI)AjBjCj£)j составлен из граней. Он имеет (АС,, ————— в)—————- ребер. вершин и диагонали )• NABCDS имеет и____диагонали (АС, )• 65 Параллелепипед разрезали на два многогранника F, и F^. Какой из получившихся многогранников выпуклый и какой невыпуклый? 51 Решение. а) Многогранник F, — параллелепипед. Он расположен по одну сторону от плоскости ______________ его грани. Следовательно, — _________________ многогранник. б) Верхняя грань многогранника является невыпуклым ______________ ^2- следовательно ____ многогранник Ответ. ^2- многогранник, _ многогранник. 66———————————- Заполните пропуски в предложении: В выпуклом многограннике сумма всех _________его вершине___________ 360°. углов при 67 Выпуклый многогранник имеет 8 вершин. Докажите, что сумма всех его плоских углов меньше 3200°. Доказательство. Так как данный __________________________ выпуклый, то сумма всех плоских ___________ при ____________ его вершине меньше __________, следовательно, сумма всех его плоских _____________ при восьми вершинах __________________ 360° •__=_______, а это________________ 3200°, что и требовалось доказать. 68 Заполните пропуски в определении призмы: Многогранник, составленный из _________ ников AjAg. А^ и . -В„, расположенных в . плоскостях, и____параллелограммов, называется многоуголь- 52 69——————————————— Какой из данных многогранников является призмой? Решение. а) Грани ABCD и многогранника и расположены в параллельных ________ _____равны . Остальные грани — параллелограммы. Следовательно, ___________________ призмой. ABCDA^Bf^D^ б) Грань КК^М^М многогранника не является Следовательно, этот многогранник призмой. в) У многогранника ABCD нет граней, расположенных в ————————— плоскостях. Следовательно, этот многогранник ——————- призмой. г) Грани АВС и А^В^С^——————— ABCA,BjC, — равные ——————, расположенные в_________________плоскостях. Остальные ____ грани являются _________________________________ Следовательно, многогранник АВСА^В^С^ призмой. 70 Сколько граней, вершин и ребер имеет п-угольная призма? Решение. а) л-угольная призма состоит из _____________ л-угольников (————-призмы) и____параллелограммов (боковых___________), т. е. имеет __ -f _ граней. б) У каждого основания л-угольной _______________ имеется __ вершин, а всего у призмы _____ вершин. 53 в) Каждое основание ______________ кроме того, имеется___боковых________ ребер равно • 2 +_____=______ Ответ, л-угольная призма имеет призмы имеет _____ сторон, . Следовательно, число всех ______ граней, ____________ 71——————————————————— Высота призмы равна 5 см. Чему равно расстояние между плоскостями оснований призмы? Решение. Основания призмы расположены в __________________ ___________плоскостях, а расстоянием между параллельными плоскостями называется___________________от произвольной——— одной из параллельных до другой плоскости. Расстоянием от данной точки до плоскости называется длина ____________________, проведенного из этой _________ к данной Поскольку высотой призмы называется проведенный из какой-нибудь точки одного _ кости другого __________________________ есть искомое_______________________между плоскостями оснований _____________к плос- то длина высоты и Ответ. см. 72 Докажите, что все боковые грани прямой призмы являются прямоугольниками. Доказательство. 1) Прямой призмой называется _____________, боковые ребра которой ____________________ к основаниям. Но если прямая перпендикулярна к плоскости, то по определению она ——— ___________к любой прямой, лежащей в этой———— . Сле- довательно, боковые ребра прямой призмы _______:——————- к сторонам основания. 2) Каждая боковая грань призмы является ————————, а параллелограмм, смежные стороны которого взаимно перпендикулярны, является___________________________. Следовательно, все боковые грани прямой призмы — ________________, что и требова- лось доказать. 54 73—————————- Докажите, что призма, две смежные боковые грани которой — прямоугольники, является прямой призмой. Доказательство. Пусть боковые грани ABBjA, и BCCjBj — прямоугольники (на рисунке изображена часть призмы). Тогда прямая ВВ. к двум пересекающимся прямым АВ и ________ плоскости основания, следовательно, ребро ___ перпендикулярно к основанию призмы. Так как все боковые____ а ребро BBj ___________________ призмы параллельны. боковые ребра________________ а значит, призма является к основанию призмы, то и все ___ к основанию ___________, ______, что и требовалось 74 Постройте диагональное сечение прямого параллелепипеда (т. е. сечение, содержащее диагональ параллелепипеда и боковое ребро). Докажите, что построенное сечение является прямоугольником. Решение. 1) Рассмотрим, например, сечение, содержащее диагональ А^С и ребро АА^. Секущая плоскость AAjC имеет с плоскостью грани ABCD две общие точки___и ___, следовательно, эти плоскости пересекаются по прямой ____, а отрезок _ Сг __ служит стороной сечения. Проведем этот отрезок. Так как АА, — CCj, то эти прямые лежат в плоскости сечения, а значит, отрезки AAj и _____— стороны сечения. Наконец, отрезок ______— четвертая сторона _____________. Проведем этот отрезок. Итак, искомое сечение — четырехугольник __________ 55 2) Так как боковые ребра параллелепипеда ____________________ и ________, то четырехугольник ЛА^С^С — ______________________. Данный параллелепипед прямой, поэтому ребро АА^ ________________ ________________к плоскости основания, следовательно, АА^__АС, а потому параллелограмм АА^С^С является что и требовалось доказать. 75 Основание прямой призмы — треугольник АВС, в котором АВ=л/т, АС-2, ВС = 2. Найдите двугранный угол при боковом ребре CCj. Решение. 1) Поскольку призма ABCA^Bfi^ прямая, то ребро CCj _________________ к плоскости АВС, а значит, АС_СС, и ВС____CCj (по _____________________ прямой, перпендикулярной к плоскости). Следовательно, угол АСВ является ________________ углом искомого двугранного угла АСС^В. 2) В треугольнике АВС (теорема________________ В, В АВ^ = АС^ + _______ — 2 ——), т.е. = _ . cos с + откуда cos С = Следовательно, А АСВ =______, т. е. двугранный угол АСС^В равен Ответ. 76 Диагональ АС основания прямой призмы ABCDA^B^C^D^ равна 6 см, а высота призмы равна gVs см. Найдите угол наклона диагонали AjC к плоскости основания. Решение. 1) Из определения прямой призмы следует, что ее боковое ребро к плоскости___________________________________и равно высоте , т. е. AAj = 6л/з см. 56 2) Поскольку прямая АА^ _________ ___________________ к плоскости АВС, то прямая АС является ______________ прямой A^C на плоскость АВС, и, следовательно, угол наклона _____________ А,С к плоскости АВС равен углу 3) Поскольку прямая АА^ ______ _______________ к плоскости АВС, то AAj __ АС (по определению прямой, ______________________ к плоскости). Из прямоугольного треугольника A^AC получаем: tgAA^CA = АА, : ________ = = _______ : ___ =_____Следовательно, АА,СА = _ Ответ. 77—- Основание призмы — равнобедренный треугольник АВС (АВ = ВС), а боковое ребро BBj образует равные острые углы с ребрами АВ и ВС. Докажите, что прямые BBj и АС взаимно перпендикулярны. Доказательство. Докажем, что проекция прямой ВВ^ на ___________ АВС перпендикулярна к прямой _____, тогда по теореме о трех __________ получим: BBj___АС. 1) Проведем перпендикуляр B^H к плоскости ____, тогда прямая ВН — ______________ прямой BBj на плоскость АВС. 2) Пусть BjM _L АВ, BJC ± ВС. Так как по условию задачи А В^ВА = = Z.____, то Л В^ВМ = А_______(по гипотенузе и острому________), следовательно, ВМ____ВК. 3) BjM J. и отрезок В^Н — к плос- кости АВС, следовательно, МН _L АВ как проекция наклонной на плоскость АВС (по обратной теореме о трех________________ Аналогично КН_____ВС. 57 4) Л ВМН_____Л ВКН (по катету и ), следова- тельно, /- МВН = Z. , т. е. отрезок ВО — треугольника АВС. 5) Так как треугольник АВС равнобедренный, ______________, то биссектриса ВО является____________ ника, т. е. ВО J_ лось доказать. АС — его треуголь- , и, следовательно, ВВ^ ___АС, что и требова- 78 Боковое ребро правильной треугольной призмы равно 4 см, а сторона основания — 6 см. Найдите периметр сечения, проходящего через ребро A^B^ и точку М — середину ребра АС. Решение. 1) Основания призмы расположены в плоскостях. В, В следовательно, секущая плоскость пере- С секает плоскости АВС и А^В^С^ по _______________________ прямым. Проведем через точку М прямую т, ________________________ прямой АВ. Обозначим точку пересечения прямых т и ВС буквой К. II АВ, АВ____следовательно, МК__________Проведем отрезки AjM и___________________________________. Четырехугольник_— искомое сечение. 2) Периметр четырехугольника А^В^КМ равен AjBj +___________+ + МА^, где A,Bj =__см и МК =_____см (МК — _________________линия треугольника АВС). Найдем длины отрезков A^M и В^К. По определению правильной призмы ее основание — ___________ треугольник, а боковые ребра_______________________к плоскости АВС. Следовательно, AM =____см и AAj____АВС. Из прямоугольного А А,AM находим: А,М = ^AAf + _____________ = = = J = ——— (см). Аналогично из прямоугольного____________ получаем: В^К = __ см. Итак, AjBj +_____________+ МА^ = 6-1-___ Ответ. Периметр сечения равен _____ см. BBjB (см). 58 79 Каждое ребро правильной шестиугольной призмы равно 4 см (достройте рисунок). Найдите площади ее боковой и полной поверхностей. Решение. 1) Любая правильная призма является призмой, следовательно, площадь ее боковой поверхности равна __________________________периметра _____________ на _________ призмы. т. е. S^^ = P—, где Р =-• 6 =. . (см). h =___см. Таким образом, = —-(см2). = бок 2) Площадь полной ______ площадей ___ Основание данной призмы — Зл/З ее граней, т. е. любой S =_ ПОЛЫ призмы ___+ 2. равна стороной а = 4 см, следовательно, ___= . шестиугольник со __• 42 =___(см2). Итак, = (. Ответ. S. =. бок + ) см2. S = ПОЛЯ § Пирамида 80 Основание пирамиды — прямоугольник ABCD, АВ = 18 м, ВС = 10 м, высота пирамиды проходит через точку пересечения диагоналей основания и равна 12 м. Найдите площадь полной поверхности пирамиды. Решение. 1) Площадь полной поверхности пирамиды вычисляется по формуле =_____________+_________. Так как основание пирамиды — _____________________________со сторонами 10 м и_______, то S = осв (м2). 59 2) Чтобы найти площадь боковой ^ ________________ пирамиды, вычислим площади ее__граней. В прямоугольнике ABCD АС_____BD, диагонали_________________в точке О, поэтому АО = ВО =_____=_______. Отре- зок МО — высота пирамиды, значит, МО — _________________________ к пло- скости основания, и отрезки АО, ВО, _____, DO — проекции наклонных AM, _____,____и_____на плоскость основания. Следовательно, AM = ВМ =___= =____и ААВМ = А_________, а А ВСМ = =_______ (по трем ______________), поэтому —- ^CDM ^ ^ВСМ -^ADM’ 3) Пусть МК -LAB, тогда ОК___АВ (обратная теорема о________ перпендикулярах) и ОК —_______ВС = 0,5’___=___ (м). Аналогично если MN ± ВС, то ON =___АВ = 0,5 •____=___(м). Поскольку МО ± АБС, то МО_______ОК, а значит, МК= ^МО’^+ = д/_+ 5^ = V = ———-(м). Аналогично MN = ^ + ON^ = = ^f_ ___=_____• 18-____=_____ (м). Итак, 5^дд^ = 0,5АБ (м^), S ВСМ S^- = 2(S^M + бок S = ПОЛИ .) = (. + _ + . (м^). . Отсюда получаем: ___) =————(м^), Ответ. 81—- Все боковые ребра пирамиды равны между собой. Докажите, что: а) высота пирамиды проходит через центр окружности, описанной около основания; б) все боковые ребра составляют равные углы с плоскостью основания. Доказательство. а) Пусть основание пирамиды — многоугольник AjA^. А^, отрезок РО — высота пирамиды. Тогда отрезки ОА^,_, . ОА^ — проекции боковых________PA^, РА^, . _на плоскость основания. Так как 60 РА^ = PAg = . =_______, то OAj_____ ___ QAg____ . _ OA^. Следовательно, точка О равноудалена от _____________ многоугольника А^А^. А^, поэтому она является________________окружности, _____________________ около основания пирамиды. б) Л AjPO = Л (по гипотенузе и . = . = Л А РО /I ___), следова- _=. =АРАО, тельно, А PAjO = А__ что и требовалось доказать. 82——————————- Основание пирамиды — параллелограмм со сторонами 6 см и 8 см, высота пирамиды равна 12 см, а все боковые ребра равны между собой. Найдите длину бокового ребра. Решение. 1) Пусть отрезок МО — высота ________________Так как МА = МВ = =_____ =_____, то ОА =______=_____= =_____, поэтому точка О — центр М около параллелограмма ABCD. Но тогда параллелограмм является _____________ _________________, диагонали которого пересекаются в точке ______ и равны друг другу. 2) По теореме Пифагора АС =^АВ^+ = (см), следовательно, ОА =____см. 3) МО ±АВС, поэтому МО____ОА. В треугольнике АМО МА =JOA^+ = J ^ = _____(см). Ответ. 61 83——————————————— Все двугранные углы при основании м пирамиды равны между собой. Докажите, что: а) высоты всех боковых граней, проведенные к сторонам основания пирамиды, равны между собой; б) высота пирамиды проходит через центр окружности, вписанной в основание. Доказательство. а) Пусть отрезок МО — высота пирамиды . А^, ОН^ J. А^А^, ОН^А-А^А^. Тогда МН^____^^2_________-^2^3 теореме о трех ________________________). Отсюда следует, что углы MHfi и ______как линейные ________равных_________________ мнр_________ углов МА^Ар и МАрр. Так как Л МНр______Л МНр (по катету и противолежащему _______), то МН^__МН^. Аналогично можно доказать равенство высот всех боковых граней пирамиды, проведенных к сторонам _______пирамиды. б) Так как Л МНр = Д_________, то ОН^__OHg. Аналогично можно доказать, что равны расстояния от точки __ до всех сторон ______________пирамиды. Следовательно, точка О —___________ окружности. в основание пирамиды, что и требова- лось доказать. 84——————————————————— Все двугранные углы при основании четырехугольной пирамиды равны между собой. Высота пирамиды равна 12 м, а периметр и площадь основания равны 48 м и 120 м^. Найдите площадь боковой поверхности пирамиды. Решение. 1) По условию задачи все двугранные углы при__________пирамиды равны, следовательно, ее высота МО проходит через _ окружности, _________________ в основание, а все высоты боковых , проведенные к сторонам основания. ______ между собой. Поэтому если h — высота боковой грани, проведенная из вершины М, то 62 S, =-AB бок 2 • л + “__________ 2 h + м )h = =____Р ■_____ ОСИ 2)Пусть МН LAB, тогда ОН_________АВ (по теореме о ________________ перпен- дикулярах), а значит, ОН — радиус __________________, вписанной в четы- рехугольник _______ 3) Площадь S многоугольника, его периметр Р и радиус г вписанной в многоугольник окружности связаны формулой ‘S = -___•___, следовательно, г = 2______: = 2 • 120 :____=____см. 4) В прямоугольном треугольнике МОН МН = h =JOH^+ -J .12^— Ответ. 85 (м). Следовательно, =-. (м2). Сторона основания правильной треугольной пирамиды равна 6 м, а боковое ребро — 4 м. Найдите: а) площадь боковой поверхности пирамиды; б) высоту пирамиды; в) площадь сечения, проходящего через боковое ребро и высоту пирамиды; г) площадь сечения, проходящего через сторону основания перпендикулярно к противолежащему боковому ребру. Решение. а) Площадь боковой поверхности правильной равна_________________произведения периметра на_________________ М боковой Апофемой правильной пирамиды называется ___________ грани, проведенная из________________пирамиды. Все боковые ребра правильной пирамиды ______________друг другу, поэтому высота МН треугольника______является и ее__________________, т. е. ВН =___ 63 -3’ = в прямоугольном треугольнике МНС МН = ^МС^— = ^ J =_________(м). Поэтому S, =_______Р ■ МН = — •_________• ВС • ____= V оок осн 2 = ————- = ——— (м^). б) Проведем высоту МО пирамиды. Так как пирамида , то точка О — ___________________________ основания, и, следо- 1 /ч ft /ч вательно, ОН =_______АН =
ВС • ——-=—— 3 (м). В прямоугольном треугольнике МОН МО = ^МН^— = л/ — (>/3)’ =73 = ——— (м)- в) Пусть плоскость сечения проходит через ребро МА и высоту пирамиды. Тогда она пересекает плоскость основания по прямой ____, а ребро ВС — в его середине — точке___Следовательно, пересечением плоскости АМН и грани ВМС служит отрезок_________ Поскольку МО АВС, то МО________АН (___________________ прямой, перпендикулярной к плоскости). Итак, S.„„ =—АН ’ АМИ 2 • Зл/з •, (М^). г) Пусть искомое сечение содержит ребро АВ и перпендикулярно к боковому__________МС. Тогда прямая МС перпендикулярна к линии пересечения секущей _____________ и грани ВМС. Итак, проведем высоту ВТ треугольника ВМС и соединим точки Т и А отрезком (выполните построения). Так как АС__ВС и Z-ACM А ВСМ (пирамида ______________________________), то Л ACT = Л_(по___сторонам и_____________между ними). Следовательно, АТС = Z._______= 90°. Итак, МС_______ВТ и МС________АТ, поэтому плоскость АВТ _______________________ к ребру МС, т. е. треугольник _______— искомое сечение пирамиды. Из равенства А ACT = ________________ следует, что АТ___ВТ, а потому медиана ТК треугольника АВТ является и ___________________, т. е. ТК J_____. Следовательно, S = — -^АСТ 2 ТК. 1 В прямоугольном треугольнике ВКТ ВК =____АВ=—_____=_____ (м). КТ = Твт^ . Найдем длину отрезка ВТ. Так как = = -ВС 2 чаем ВТ = МС , то ВС ВТ, откуда полу- вс-мн — — _ V^(M). 64 Поэтому КТ _ L л ‘ !VZ (“)■ Следовательно, =___ Ответ, а) = r)S^,=———- _-^л/з =_ 2 б) МО = (м% ; в) S АМН 86——————————- Боковое ребро правильной шестиугольной пирамиды равно 5 см, а сторона основания — 6 см. Найдите площади ее боковой и полной поверхностей. Решение. 1) Площадь боковой поверхности правильной пирамиды равна произведению _______________________ основания на •9. М где q = MK=^ = ____(см). —» т.е. S^^ = . -СК СК=
. 2 Итак, q = ^ — 3^ = ^ = ____(см), Р = 6 __ • ___ = ______ (см^). —- = —— (см). = бок 2)S =. ‘ ПАПН Следовательно, О т 1 87 , + S , где S = оси’ ОСЯ =_________-I-______ 3a^V3 3 = „ = ——Уз (см^). . (см^). О т в е т. S. = . бок , S = Все ребра четырехугольной пирамиды равны между собой. Докажите, что пирамида правильная. Доказательство. 1) Стороны четырехугольника ABCD — основания пирамиды MABCD — ___________ между собой, следовательно, этот четырех- угольник является 2) Боковые ребра прамиды около ее основания можно описать санный в окружность, является____ сечения диагоналей является его центром. между собой, поэтому _________Но ромб, впи- _______, а точка О пере- 65 3) в треугольнике АМС AM_________МС, АО_____ОС, следовательно, МО____________________________________АС. Аналогично в треугольнике BMD МО_BD. Поэтому отрезок МО —________________________________________ к плоскости основания пирамиды (____________________________________________ перпендикулярности прямой и плоскости). Итак, основание пирамиды — квадрат, т. е. _____________________ четырехугольник, а отрезок, соединяющий вершину пирамиды с ____________основания, является высотой пирамиды. В соответствии с определением пирамида___________________________ , что и требовалось доказать. 88————————————————————— Плоскость, параллельная основанию треугольной пирамиды, делит ее высоту в отношении 1:2, считая от вершины пирамиды. Докажите, что эта плоскость делит боковые ребра в том же отношении. Доказательство. Так как плоскости AjBjCj и_______ параллельны, то А^В^—АВ (——————— параллельных плоскостей). Аналогично BjCj__ВС, AjCj___АС и AjOj__АО. М Поэтому МА, MCi ^ MAi CiC ______ Итак, 89 AMi А, А MOi MBi MBi BiB МА, MOi 1 _ —-= —, ЧТО и требовалось доказать. Правильная четырехугольная пирамида со стороной основания 10 см и боковым ребром 13 см пересечена плоскостью, параллельной основанию и проходящей через середину высоты пирамиды. а) Постройте сечение пирамиды данной плоскостью. б) Найдите апофему, высоту и площадь полной поверхности усеченной пирамиды. Решение. а) Пусть точка Oj — середина высоты МО, плоскость а — секущая. Так как а___АВС, то плоскость АМС пересекает плоскости АВС и а по______________________прямым АС и а. Проведем прямую а и обо- 66 значим точки ее пересечения с ребрами МС и______через Cj и А,. Аналогично плоскость MBD пересекает плоскости АВС и а по ___________ _________________ прямым______и -Bj-Di (В^еМВ, D^€:MD). Соединим точки А^, Sj, Cj и Dj последовательно отрезками и получим четырехугольник A^B^C^D^ — искомое ___________пирамиды. б) Проведем в грани МВС апофему МН пирамиды MABCD. Тогда Н^Н — _____________ усеченной пирамиды ABCDA^Bf^^Dy Так как плоскости А^В^С^ и АВС_____________________________, то О.я, II— м _____________. Но МО^ = OjO, следовательно, МН^__Н^Н. В треугольнике МНС катет МН = = 4мс^
= 7= =_____ (см). Поэтому НjH =_____МН= -•i——_(см). в треугольнике МОН Ofi =_____МО = — -______________ =____л/ (см). = Площадь боковой ABCD равен_____ВС = 4 равна произведению ___ на ____________ М правильной усеченной __________ периметров __=______(см). Найдем периметр основания A^B^Cfi^. Плоскости AjBjCj и АВС ________________ Периметр основания , следовательно. плоскость МВС пересекает их по_________________________________ прямым, т. е. BjCj__ВС. Так как МН^_____Я^Я, то BjCj — средняя ___________ треугольника МВС, поэтому BjCj =______ВС. Следова- периметр четырехугольника A^B^C^D^ равен половине _______________ четырехугольника ABCD, т. е. Р= — Р или 1 О тельно, л = 40 = (см). 67 Итак, =-(Л+ )-Я,Я=-(_________+_____)• = -_____• = ’ бок о ^ 1 —‘ 1 О ‘— ‘ — о (см^). Ответ, б) Апофема_____ сота — ______см, площадь . пирамиды равна___см, вы- поверхности —______(см^). § Правильные многогранники 90 Заполните пропуски. Точки М и Mj называются симметричными относительно: точки А Ml точка А —___________ отрезка ММ^. Точка А считается самой себе. 68 91 Диагонали куба ABCDA^B^C^D^ пересекаются в точке О. Найдите вершину, симметричную вершине D относительно: а) точки О; б) прямой АС; в) плоскости ACCj. Решение. а) Точка О является _____________ отрезка DB^, следовательно, вершины D и _____ симметричны относительно _________О. б) Диагонали квадрата ABCD взаимно и делятся точкой пересечения_________ D АС проходит через середину отрезка BD и нему, т. е. точки D и В ______________ _____________АС. . Следовательно, прямая ______________________к относительно в) Так как AA^±ABD, то AAj___________BD (определение прямой, ——————— к плоскости). Кроме того, BD_____АС. Таким образом, прямая BD перпендикулярна к двум_______________________ прямым (AAj и АС) плоскости________, поэтому BD___ACC^ (признак перпендикулярности___________и плоскости). Прямая АС пересекает отрезок BD в его_________. Следовательно, плоскость АСС^ проходит через ____________ отрезка BD и перпендикулярна к нему, поэтому точки В и D______________________ Ответ, а) Вершина 92————— относительно плоскости ACCj. ; б) вершина ; в) вершина Заполните пропуски: а) Точка называется точка фигуры симметрии фигуры, если _________ относительно нее некоторой точке той же б) Прямая называется осью дая точка фигуры симметрична __________той же фигуры. в) Плоскость называется___ фигуры, если каж-____нее некоторой симметрии фигуры, если относительно нее фигуры. 69 93——————————- Сколько центров, осей и плоскостей симметрии имеет правильная четырехугольная пирамида? Ответ. У правильной четырехугольной пирамиды нет _______________ симметрии; (прямая симметрии и_________ ось ___ —); — (КМН, ). плоскости АМС 94———————————————————- Заполните пропуски в определении правильного многогранника: Выпуклый ________________________ называется правильным, если ______ его грани —__________________ многоугольники, и в его сходится одно и то же число 95 Докажите, что куб является правильным многогранником. Доказательство. Проверим, обладает ли куб всеми признаками правильного __________________, указанными в определении. 1) Куб______________выпуклым многогранником. 2) Каждая грань куба —___________, т. е.___________________ многоугольник, и все грани 3) В_______________ сходится ______________ между собой. . вершине куба ______ число все ребер, а именно___ребра. Итак, у куба ____________ признаки, указанные в определении _______________________ многогранника. Следовательно, куб правильным ________ что и требовалось доказать. 70 96 Вершины А, С, В, и куба соединены попарно отрезками. Докажите, что многогранник ACB^Dj является правильным. Доказательство. 1) Получившийся многогранник ACB^D^ — тетраэдр, а известно, что тетраэдр ____________________ выпуклым многогранником. 2) Все ребра многогранника ACBjBj являются _____________________ граней куба, следовательно, они __________ между собой, а потому все грани многогранника ACBjBj являются правильными _______________________________ 3) В каждой вершине ____________ С / 1 1 / А / ^ / ✓ щ / ✓ / ✓ •к» «Ч ^ •ч Чц количество Итак, у тетраэдра ACBjBj ____ ACBjBj сходится ., а именно __ребра. все признаки правиль- ного многогранника, следовательно, многогранник. этот тетраэдр — 97 От куба отсечены 8 тетраэдров так, что все грани получившегося многогранника — правильные многоугольники. Является ли этот многогранник правильным? Решение. Проверим наличие признаков, указанных в определении правильного — 1) Данный многогранник__________ ________ выпуклым. 2) В каждой вершине сходится число ребер (— ребра). 3) Все грани — правильные—————- они равны друг другу: треугольник———- Следовательно, данный многогранник правильным. ________, но не все восьмиугольнику. 71 98———————————————————- Запишите в таблицу значения параметров: л — число сторон грани правильного многогранника; k — число ребер, сходящихся в одной вершине; В — число вершин многогранника; Р — число ребер; Г — число граней. Напишите названия многогранников. Вычислите для каждого из них величину В -f Г — Р. 72 99 а) Дорисуйте на развертке правильного октаэдра клапаны для склеивания, добавляя их через одно ребро. Вырежите развертку и склейте модель многогранника. б) Измерьте длину ребра и вычислите площадь поверхности правильного октаэдра. Ответ, б) см‘ 73 ,!i V .i:^ : ‘/ГгТЦ’^1и::*^ w »4 .’i •,’;>;•/ . ta if i7 V^..’л ^ idn-^ fj.j4>;vr . ,y Л vij :.t’ ‘ »• iK. X :• ‘■■/ 1^с| =_см. 80 § Сложение и вычитание векторов. Умножение вектора на число 106 Cl Дан параллелепипед ABCDA^Bfi^D^. 1) Постройте вектор, начало и конец которого являются вершинами параллелепипеда, равный сумме векторов: а) АА, и DC’, б) DC и АА,. 2) Сравните суммы векторов AA^+DC и DC + AA^. Решение. 1) Для построения суммы _________ используем правило треугольника. а) От конца вектора АА, — точки__— отложим вектор_______, равный вектору DC. Суммой векторов АА, и А,В, является вектор______ (изобразите его на рисунке). Итак, АА, -I- DC = АА, ____ = —— б) Откладывая от конца вектора DC вектор______, равный вектору ______, получаем: DC + АА= DC+______=_____(изобразите этот вектор на рисунке). 2) Начала и концы полученных векторов ________ и ——- слу- жат вершинами четырехугольника АПС,В,, который является _____________________________. Следовательно, АВ, =___и лучи АВ, и __сонаправлены, а значит, АВ, = ВС,. Итак, АА, + DC = ______ + АА,. 107 Дан параллелепипед ABCDA^B^C^D^. Найдите сумму векторов АВ -ЬАА, + AD. Решение. Пер = (АВ + вый способ. АВ + АА, -f АВ = .)+АВ (. закон). Так как грань АВВ^А^ является __________________________, то по правилу параллелограмма получаем: Cl Pi 81 АВ + AAj=______Четырехугольник ABfi^D — _________, следовательно, по правилу _____ AB, + AD =____ Итак, AB + AAj+AD = (_+ АА^) + . + AD = Второй способ. АВ +AAj+AD = АВ+(АА,+_______) (. _________ закон). Грань AA^DJ) —_______________ следовательно, по правилу_________ =______Четырехугольник AD^C^B — следовательно, по правилу ________ AB+AD.=_______ Ответ. AB + AA^+AD = AA, + AD = Итак, АВ + АА,+ AD=(AB+_) +_= АВ + (_+AD)=. 108 Дан параллелепипед ABCDA^B^CJ)^. Докажите, что АВ-I- СА-I- ^ = A^j-Ь ВА J-Н . Доказательство. 1) АВ + СА+^ = = (АВ + _) + BD = = (СА + __)+BD = = ___ + BD = 2) A,Dj-f- BAj+ CjB = = ——————) = = A^D,+ iC,B+——) = = A,Dj -I- + AjDi = Обоснование. правило. правило. _______закон _______закон треугольника закон закон 361КОН треугольника Cl Грань CODjCj параллелепипеда является 4- _ 82 = AjDj -f- , следовательно, CD____C^D^. Поэтому АВ + СА-1- __ -I- CjB, что и требовалось доказать. концом и нача-параллелепипеда 109————- Какие векторы с лом в вершинах а) противоположны вектору АС б) равны вектору -CD^, в) равны разности AAfAC ; г) равны сумме ВА + (-СД); д) равны вектору — CD-АС ? Решение. а) Два ненулевых __________ если их длины_________и они _ ‘Сг называются противоположными, __________________ направлены. В параллелепипеде ABCDA^B^C^D^ АС =. правлены по отношению к лучу АС лучи . . Противоположно на- и Следовательно, вектору АС противоположны векторы . б) Запись -CI)j означает вектор, __________________ и. вектору CjDj. Равными этому вектору являются векторы—-и _ в) Разность векторов АА^-АС можно найти двумя способами: 1) по определению разности двух_____________ 2) используя формулу а — Ь = а + (-). 1) По определению разностью векторов АА, и АС является такой _____________ X, сумма которого с вектором_____рав- на вектору_____, т. е. АС +—=—— Значит, искомый вектор х — это вектор _____, т. е. АА^-АС =___ _____________________________^ ^ 2) Используя формулу а — Ь = а + (____), получаем: АА^-АС = = AAj+(-_____). Но вектор-АС —это вектор, ——————- ______________вектору_____, т. е. вектор___. Поэтому AAj-AC = = AAj+ = СА + г) Как установлено в п. «б», -CD^= — Следовательно, ВА+ д) —- 9 — 83 110————————————————— Докажите, что АВ — CD = АВ + DC. Доказательство. Используя формулу а — Ь =____+ (- Ь ) и равенство -CD=DC, получаем: AB-CD=AB+ (-__________)= АВ+-, что и требовалось доказать. 111 Упростите выражение: а) AB-i^ + MC-MO-дк; б) КМ -АР-РМ + СЕ — СА. Решение. а) АВ-КВ+______-м6-дк=АВ+ВК + МС+___-ОК = + ОМ + МС + ( — _) = АК + _ -Ь _ = АК+ __ = АО + __ = _____ ^ КМ- АР — РМ + СЕ — СА = КМ — РМ -_- СА + = КМ+____+ РА+___+ СЕ = КР +__+ СЕ =___+ + + ОС = Ответ, а) ; б) 112 Даны точки К, М, Р, О. Представьте вектор КМ в виде алгебраи-^ ческой суммы векторов: а) МО, КР, ОР; б) РМ, ОК, РО. Решение. а) Используя равенства КМ=КР + РО+ _____, РО = — ___, ОМ = -____, получаем: КМ = ___ — ___ — ____ б) КМ=^+ ______ + ____ = — ____ — ____ + ___ Ответ. а) КМ =_______________; б) =__________________ 113 Заполните пропуски: Произведением .вектора а на k назы- , такой, что |Ь| = |_|‘|___|, причем Ь |Т___ вается ___________ при к> о и Ь___а при к О, то векторы 1 • а и а _____________________________________Следовательно, по определению —► —► равных векторов 1 • а ___ а. б) По определению ________________________ вектора на число как -1 ____ О, то |(-1)- а! = |-1-|—1 = —-|—1 = |а|, а ^ак (-1) • а tie. Следовательно, векторы (-1) • а и ___противоположны, т. е. (-1) • а__- а . 115 Дана треугольная пирамида МАВС, МА = а , МВ = Ь , МС = с . а) Отложите от точки М вектор: X =
Ь ; у=-с; z=-b+-c; 2^2 2 2 т— а — Ь — с. 2 2 б) Отложите от точки А вектор п = — т . 3 М _____?С Решение. а) Так как х » то по определению произведения вектора на ______ X ft___и IX I =__I Ь |. Отметим середину ребра МВ — точку Е, тогда ME =___Ь = X. Аналогично отметим точку Н — ____________ ребра МС, тогда МН= ___с = ______ Так как z=-b+-__, то z = ME + 2 2 _ . Построим вектор z по параллелограмма. Для этого через точку Е проведем , параллельную прямой МС, а через точку Н — прямую. 85 прямой . По теореме эти прямые пересекут отрезок ВС в его_____ буквой К. Тогда г =_____ т= а——о———= а — Ь______- с ) 2 2 2 2 __________закон. Но — & + -___= г =МК, а = 2 2 . Обозначим эту точку первый следовательно, т =. , т. е. МА = + т. Поэтому т =. б) Так как га = — — и — — О, то га_______гаг и 1 га | =_| гаг |. Отло- 3 3 жим от точки А вектор га . Для этого на отрезке АК нужно отметить точку О так, чтобы АО =____АК. Тогда АО = ___АК =_______т = п . 116 Упростите выражение 2(5 а — 3 с ) — 3(3 а — 2 с ). Обоснование. Решение. 2(5‘а — _)-3( ) = = 2(5 а)-__-3(3 а). = 10 а — _ — 9 а__ = 10а-9а — _______ = (10-9)7- _______ = 1 а — __ = ___ Ответ. распределительный закон ——————закон ________________________________и переместительный законы сложения ____________________________ закон 117 Докажите, что если векторы о и 6 коллинеарны и а 0, то существует такое число к, что Ь = к а . Доказательство. Возможны два случая: 1) а]Ь и 2) о—Ь . В обоих случаях векторы лежат на одной прямой или на ——————-прямых, т. е. лежат в одной плоскости. 1) Пусть а It 5. Возьмем число Л = <^. Тогда |fta| = |_|•|a| = in in = Ы • I-1 = I Ь |. Так как к_0, то ft а 11_Следовательно, Ъ___ft а . а Итак, для первого случая утверждение доказано. 86 2) Пусть ai b . Возьмем число k = -—Тогда |А а | = |А| • |_| = = -j^ • I_I = I_|. Так как к
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельные прямые в пространстве. Параллельность трех прямых
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
На этом уроке мы дадим основные определения и теоремы на тему параллельных прямых в пространстве.
В начале урока рассмотрим определение параллельных прямых в пространстве и докажем теорему о том, что через любую точку пространства можно провести только одну прямую, параллельную данной. Далее докажем лемму о двух параллельных прямых, пересекающих плоскость. И с ее помощью докажем теорему о двух прямых, параллельных третьей прямой.
Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Геометрия. 10 класс
Конспект урока
Геометрия, 10 класс
Урок №4. Параллельность прямых, прямой и плоскости
Перечень вопросов, рассматриваемых в теме
- Определение параллельных прямых;
- Теорема о единственности прямой, параллельной данной, проходящей через данную точку;
- лемма о двух параллельных прямых;
- теорему о параллельности трех прямых;
- определение параллельных прямой и плоскости;
- признаком параллельности прямой и плоскости.
Глоссарий по теме
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.
Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.
Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.
Теоретический материал для самостоятельного изучения
Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.
В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».
В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».
В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.
В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.
Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Давайте укажем некоторые пары параллельных прямых:
AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.
А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:
AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.
Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.
- М и а задают плоскость α
- Прямая, проходящая через точку М параллельно прямой а, должна лежать в одной плоскости с точкой М и прямой а, т.е. в плоскости α.
- В плоскости α через точку М проходит прямая, параллельная прямой а, и притом только одна- это нам известно из кураса планиметрии.
- На чертеже эта прямая обозначена буквой b .
- Следовательно, b-единственная прямая, проходящая через точку М паралельно прямой а.
Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.
Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

- Рассмотрим две параллельные прямые a и b и допустим, что прямая b пересекает плоскость α в точке M(а рис.).
- Мы знаем, что через параллельные прямые a и b можно провести только одну плоскость β. (теорема)
- Так как точка M находится на прямой b, то M также принадлежит плоскости β (б рис.). Если у плоскостей α и β есть общая точка M, то у этих плоскостей есть общая прямая p, которая является прямой пересечения этих плоскостей (4 аксиома).
- Прямые a, b и c находятся в плоскости β.
Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.
- Точку пересечения прямых a и p обозначим за N.
Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.
- Значит, прямая a пересекает плоскость α в точке N.
Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.
Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:
|
|
|










 . BC=AD= 8 см;
. BC=AD= 8 см;