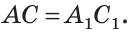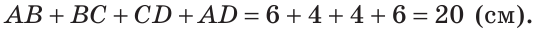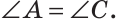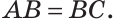Обоснуйте равенство треугольников на рисунке

Ответ:

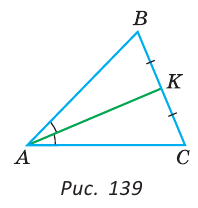
Треугольник ADC = ABE.

Объяснение:

Треугольник ABD — равнобедренный, значит, угол ABD = ADB.

И в треугольнике углы ABD + ADB + BAD = 180°.

Но углы ABD + DBE + нижний B = 180°, причем ABD = ADB = нижнему B.

Отсюда BAD = DBE = 180° — 2*ABD

При этом углы BAD = DAC, значит, ACD = DEB.

Следовательно, треугольники ADC и BDE подобны по трем углам.

Теперь рассмотрим треугольники ADC и ABE.

Стороны AB = AD, углы DAC = BAE, ACD = AEB, ADC = ABE.

Эти треугольники равны по стороне и двум углам, прилежащим к ней.

Видео:Признаки равенства треугольников. Доказать равенство по рисунку. Найти пары.Скачать

Признаки равенства треугольников — определение и вычисление с примерами решения

Содержание:

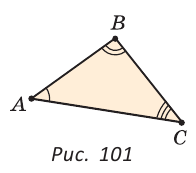
Если на плоскости отметить три точки А, В и С, не лежащие на одной прямой, и соединить их отрезками, то получим треугольник ABC. Можно сказать, что треугольник — это трехзвенная замкнутая ломаная. Обозначают:

Видео:первый признак равенства треугольников. Задачи по готовым чертежам, рисункам. 7 классСкачать

Определения

Определение. Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.

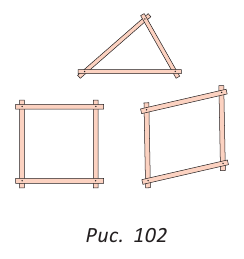
Если соединить концами три деревянных планки, то получится треугольник, который нельзя подвергнуть деформации — он будет сохранять свою форму. Тогда как четырехугольник может менять свою форму (рис. 102)? Это свойство «жесткости» треугольника широко используется в технике, производстве, строительстве.

Равные треугольники

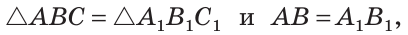
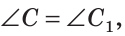
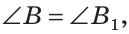
Равные треугольники можно совместить наложением так, что соответственно совпадут все три стороны и все три угла (рис. 103). В совпавших, то есть в равных треугольниках, против равных сторон лежат равные углы, а против равных углов — равные стороны. Если то а если то

Для совмещения равных отрезков достаточно совпадения их концов, а для совмещения равных треугольников — совпадения их вершин.

Виды треугольников

Если у треугольника все три стороны имеют разную длину, то такой треугольник называется разносторонним.

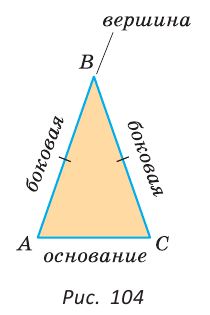
Треугольник, у которого две стороны равны, называется равнобедренным. Его равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника (рис. 104).

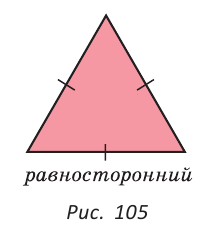
Если у треугольника равны все три стороны, то он называется равносторонним (рис. 105). Равносторонний треугольник является также и равнобедренным, где любую пару сторон можно принять за боковые стороны.

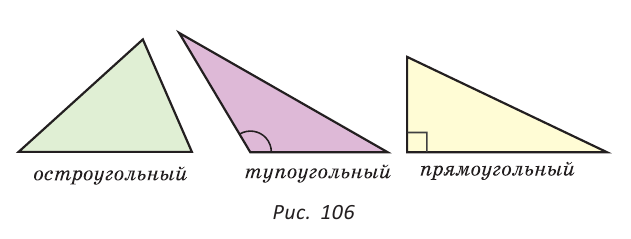
По величине углов треугольники делятся на остроугольные (у них все углы острые), тупоугольные (есть тупой угол) и прямоугольные (есть прямой угол) (рис. 106).

Треугольником называется трехзвенная замкнутая ломаная вместе с частью плоскости, которую она ограничивает.

Периметром треугольника (многоугольника) называется сумма длин его сторон.

Равными треугольниками называются треугольники, которые можно совместить наложением.

Равнобедренным треугольником называется треугольник, у которого две стороны равны.

Равносторонним треугольником называется треугольник, у которого все стороны равны.

Свойство равных треугольников. В равных треугольниках против равных сторон лежат равные углы, а против равных углов — равные стороны.

Замечание. Называя или записывая равные треугольники, стараются соблюдать последовательность соответствующих вершин. Во многих случаях это удобно. Однако делать это необязательно. Обе записи: АВС =KNM и BAC =KNM — правильные. Иногда соответствующие вершины равных треугольников обозначают одними и теми же буквами, добавляя к буквам одного из треугольников индекс: АВС = = А₁В₁С₁. При такой записи имеют в виду, что соответствующими являются вершины А и А₁, В и В₁, С и С₁.

Первый и второй признаки равенства треугольников

При выяснении равны ли треугольники нет необходимости устанавливать равенство всех их соответствующих элементов путем наложения или измерения. Следующие две теоремы гарантируют равенство треугольников при равенстве некоторых сторон и углов.

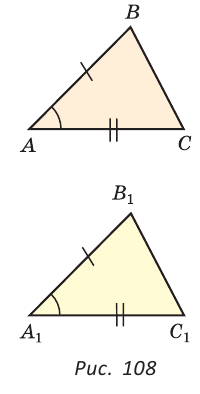
Теорема (первый признак равенства треугольников). Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

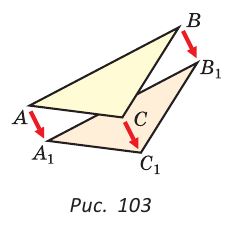
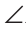
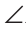
Дано: АВ =А₁В₁, АС =А₁С₁, A = A₁ (рис. 108).

Доказать: АВС = А₁В₁С₁.

Доказательство:

Наложим треугольник ABC на треугольник А₁В₁С₁ так, чтобы совпали равные углы А и А₁, луч АВ совпал с лучом А₁В₁, а луч АС совпал с лучом А₁С1. Так как отрезки АВ и А₁В₁ равны, то они совпадут при наложении, и вершина В совпадет с вершиной В₁. Аналогично совпадут равные отрезки АС и A₁C₁, вершина С совпадет с вершиной C₁. Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, АВС = А₁В₁С₁. Теорема доказана.

Говорят, что две стороны и угол между ними задают треугольник однозначно.

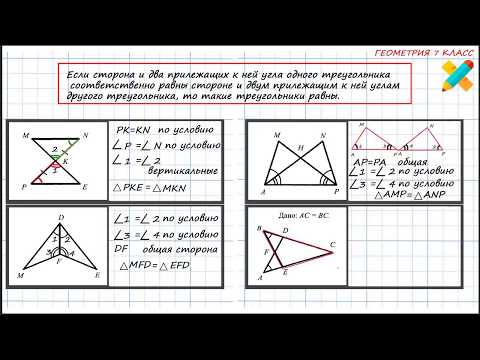
Теорема (второй признак равенства треугольников). Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

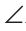
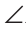
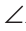
AC =А₁С₁, A = А₁, C = С₁ (рис. 109).

Доказать: АВС = А₁В₁С₁.

Доказательство:

Наложим треугольник ABC на треугольник А₁В₁С₁ так, чтобы совпали равные стороны АС и А₁С₁, угол А совпал с равным углом А₁, а угол С — с равным углом Сх. Тогда луч АВ совпадет с лучом А₁В₁, луч СВ — с лучом С₁В₁, а вершина В совпадет с вершиной В₁ (точка В будет принадлежать и прямой
А₁В₁, и прямой С₁В₁, и поэтому совпадет с точкой их пересечения В₁). Треугольники совпадут полностью, так как совпадут их вершины. Таким образом, АВС = А₁В₁С₁. Теорема доказана.

Говорят, что сторона и два прилежащих к ней угла задают треугольник однозначно

Пример №1

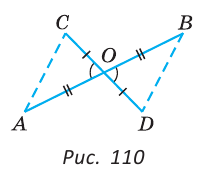
Отрезки АВ и CD пересекаются в их серединах. Доказать, что расстояния между точками А и С, В и D равны.

Доказательство:

Пусть О — точка пересечения отрезков АВ и CD (рис. 110). Рассмотрим АОС и BOD. У них АО = ОВ, CO = OD по условию, AOC = BOD как вертикальные. Треугольники равны по двум сторонам и углу между ними, то есть по 1-му признаку равенства треугольников. Стороны АС и BD равны, так как в равных треугольниках против равных углов лежат равные стороны.

Возможно краткое оформление решения задачи.

Пример №2

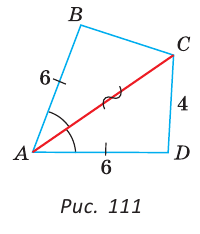
Дана простая замкнутая ломаная ABCD, у которой АВ =AD = 6 см, CD -4 см и луч АС является биссектрисой угла BAD. Найти длину ломаной ABCD.

Решение:

У треугольников ABC и ADC сторона АС — общая (рис. 111), AB=AD по условию, BAC =DAC, так как АС — биссектриса угла BAD.

Эти треугольники равны по 1-му признаку равенства треугольников.

Отсюда ВС = CD как соответствующие (соответственные) стороны в двух равных треугольниках.

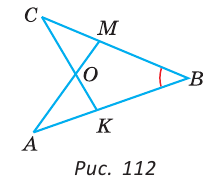
Длина ломаной ABCD:

Пример №3

На сторонах угла В отложены отрезки: ВА = ВС, КА-МС (рис. 112). Доказать, что A = С.

Доказательство:

Рассмотрим треугольники АВМ и СВК. У них B — общий, АВ = СВ по условию, MB=KB, так как MB = СВ — СМ, KB =АВ -АК (если от равных отрезков отнять равные, получим равные отрезки). Треугольники АВМ и СВК равны по двум сторонам и углу между ними. Из равенства треугольников следует, что A = C (в равных треугольниках против равных сторон лежат равные углы).

Пример №4

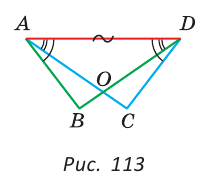
На рисунке 113 BAD = CDA, CAD = BDA. Доказать равенство треугольников АОВ и DOC.

Доказательство:

Так как ABD =DCA по 2-му признаку равенства треугольников (сторона AD — общая, углы при стороне AD соответственно равны по условию), то АВ = DC, B =C.

Так как BAO = BAD — CAD, CDO = CDA — BDA, тo BAO =CDO (если от равных углов отнять равные, получим равные углы). Тогда АОВ = DOC по 2-му признаку равенства треугольников.

Высота, медиана и биссектриса треугольника

У треугольника, помимо трех сторон, трех вершин и трех углов, имеются также и другие элементы — высота, медиана и биссектриса.

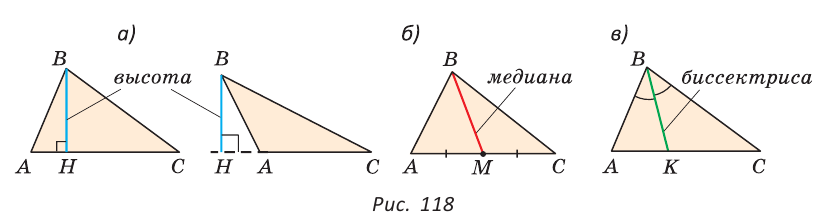
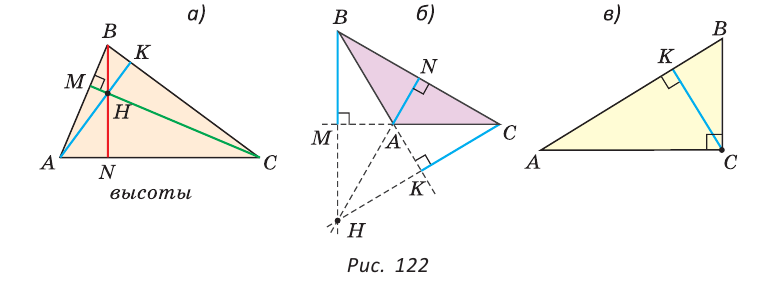
Определение. Высотой треугольника (рис. 118, а) называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на ее продолжение (отрезок ВН).

Определение. Медианой треугольника (рис. 118, б) называется отрезок, который соединяет вершину треугольника с серединой противоположной стороны (отрезок ВМ).

Определение. Биссектрисой треугольника (рис. 118, в) называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения биссектрисы с противоположной стороной (отрезок ВК).

В равных треугольниках равны соответствующие высоты, медианы и биссектрисы.

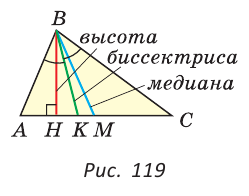
Если треугольник не равнобедренный, то высота, медиана и биссектриса, проведенные из одной вершины треугольника, не совпадают (рис. 119).

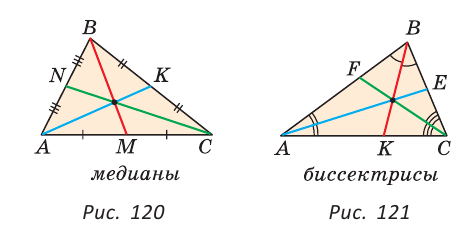
Поскольку у треугольника три вершины, то у него и три высоты, три медианы, три биссектрисы. Позже мы докажем, что высоты треугольника (или их продолжения) пересекаются в одной точке. Это же касается медиан треугольника (рис. 120) и его биссектрис (рис. 121).

Если треугольник остроугольный (рис. 122, а), то точка пересечения его высот находится внутри треугольника ABC. Если треугольник тупоугольный или прямоугольный (рис. 122, б, в), то продолжения высот пересекаются соответственно вне треугольника или в вершине прямого угла.

Точки пересечения высот, биссектрис и медиан называются замечательными точками треугольника.

Геометрия 3D

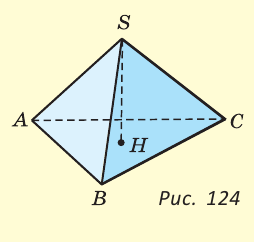
Тетраэдром или треугольной пирамидой называется многогранник, у которого все четыре грани — треугольники. Любую его грань можно принять за основание, а противолежащую вершину — за вершину пирамиды. Если точка S — вершина, а треугольник ABC — основание пирамиды, то перпендикуляр SH к плоскости ABC является высотой тетраэдра (рис. 124).

Равнобедренный треугольник

Определение. Треугольник называется равнобедренным, если у него две стороны равны.

Равные стороны называются боковыми сторонами, третья сторона — основанием, вершина, противолежащая основанию, — вершиной равнобедренного треугольника.

Рассмотрим некоторые свойства равнобедренного треугольника и один из его признаков.

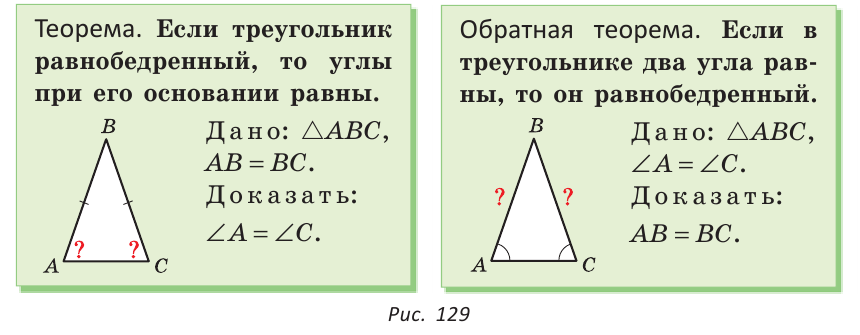
Теорема (о свойстве углов при основании). В равнобедренном треугольнике углы при основании равны.

Дано: 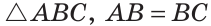(рис. 126).

Доказать:

Доказательство:

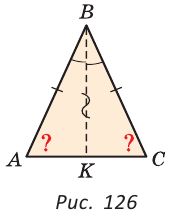
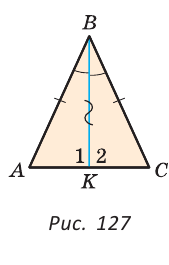
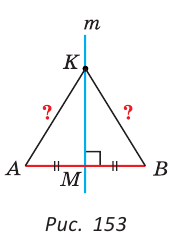
Проведем биссектрису ВК треугольника ABC. Треугольники АВК и СВК равны по двум сторонам и углу между ними: сторона ВК — общая, АВ = ВС по условию, углы АВК и СВК равны по определению биссектрисы. Из равенства этих треугольников следует, что 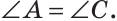Теорема доказана.

Теорема (о свойстве биссектрисы равнобедренного треугольника).

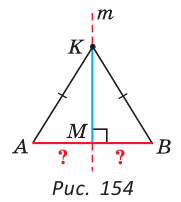
В равнобедренном треугольнике биссектриса, проведенная к основанию, является его медианой и высотой.

Дано: 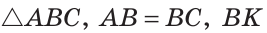— биссектриса (рис. 127).

Доказать: ВК — медиана и высота.

Доказательство:

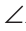
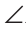
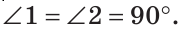
Треугольники АВК и СВК равны по двум сторонам и углу между ними (см. предыдущую теорему). Из равенства треугольников следует, что АК=КС и 1 =2. Так как углы 1 и 2 смежные, то их сумма равна 180°, поэтому Следовательно, ВК — медиана и высота. Теорема доказана.

Замечание. Поскольку из вершины треугольника можно провести только одну биссектрису, одну высоту и одну медиану, то теорему можно сформулировать так: «Биссектриса, высота и медиана равнобедренного треугольника, проведенные из вершины к основанию, совпадают». То есть если по условию задачи дана высота равнобедренного треугольника, проведенная к основанию, то согласно данной теореме она является биссектрисой и медианой. Аналогично, если дана медиана равнобедренного треугольника, проведенная к основанию, то она является высотой и биссектрисой.

Теорема (признак равнобедренного треугольника). Если в треугольнике два угла равны, то он равнобедренный.

Дано:

Доказать:

Доказательство:

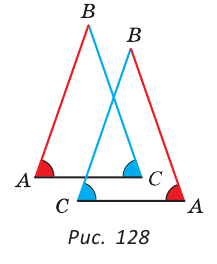
Мысленно перевернем треугольник ABC обратной стороной (рис. 128) и наложим перевернутый треугольник на треугольник ABC так, чтобы их стороны АС совпали, угол С совпал с углом А, угол А совпал с углом С.

Тогда перевернутый треугольник совместится с данным, и сторона ВС совместится со стороной АВ. Следовательно, АВ = ВС, т. е. АВС — равнобедренный. Теорема доказана.

Доказанный признак равнобедренного треугольника является теоремой, обратной теореме о свойстве углов при основании равнобедренного треугольника (рис. 129).

Напомним, что любая теорема состоит из условия — того, что дано, и заключения — того, что нужно доказать. У теоремы, обратной данной, условием является заключение данной теоремы, а заключением — условие данной.

Пример №5

Доказать, что в равнобедренном треугольнике биссектрисы, проведенные к боковым сторонам, равны между собой.

Доказательство:

Пусть в АВС АВ =ВС, АК и СМ — биссектрисы (рис. 130). Нужно доказать, что АК = СМ. Рассмотрим АКВ и СМВ. У них B — общий, АВ = ВС по условию, BAK = BCM как половины равных углов А и С при основании равнобедренного треугольника. Тогда АКВ = СМВ по 2-му признаку равенства треугольников, откуда АК = СМ. Что и требовалось доказать.

Замечание. Вторым способом доказательства будет рассмотрениеАКС иСМА и доказательство их равенства.

Пример №6

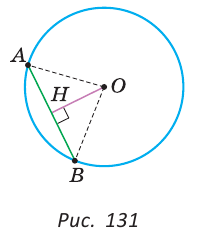
Доказать, что перпендикуляр, проведенный из центра окружности к хорде, делит эту хорду пополам.

Доказательство:

Пусть О — центр окружности, АВ — хорда, ОН — перпендикуляр к хорде АВ (рис. 131).

Отрезки OA и ОВ равны как радиусы. Поэтому треугольник АОВ — равнобедренный, а ОН — его высота, проведенная к основанию. Мы знаем, что высота равнобедренного треугольника, проведенная к основанию, является и медианой. А медиана делит сторону треугольника пополам, то есть АН = НВ. Что и требовалось доказать.

Признаки равнобедренного треугольника

Вы уже знаете один признак равнобедренного треугольника: «Если в треугольнике два угла равны, то треугольник равнобедренный». Докажем еще три признака равнобедренного треугольника, связанных с его высотой, медианой и биссектрисой.

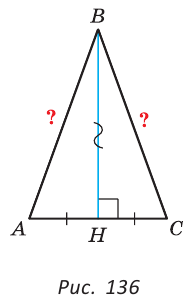
Теорема. Если в треугольнике высота является медианой, то треугольник равнобедренный.

Дано: ВН — высота и медиана АВС (рис. 136).

Доказательство:

Рассмотрим АВН и СВН. У них сторона ВН — общая, (так как ВН — высота), АН = СН (так как ВН — медиана). Треугольники АВН и СВН равны по двум сторонам и углу между ними. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.

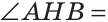
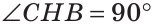
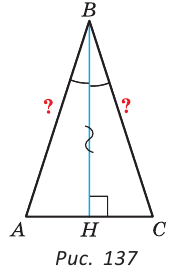
Теорема. Если в треугольнике высота является биссектрисой, то треугольник равнобедренный.

Дано: ВН — высота и биссектриса АВС.

Доказать: АВ = ВС (рис. 137).

Доказательство:

Рассмотрим АВН и СВН. У них сторона ВН — общая, (так как ВН — высота), (так как ВН — биссектриса). Треугольники АВН и СВН равны по стороне и двум прилежащим к ней углам. Из равенства треугольников следует равенство соответствующих сторон АВ и ВС. Теорема доказана.

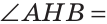
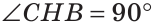
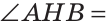
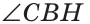
Теорема. Если в треугольнике медиана является биссектрисой, то треугольник равнобедренный.

Дано: ВМ — медиана и биссектриса АВС.

Доказать: АВ = ВС (рис. 138).

Доказательство:

Продлим медиану ВМ на ее длину за точку М. Получим МВХ = ВМ. Треугольники АМВ₁ и СМВ равны по двум сторонам и углу между ними (МВ₁ = ВМ по построению; AM = МС, так как ВМ — медиана; AMВ₁ =CMB как вертикальные). Из равенства этих треугольников следует, что АВ₁=ВС и AB₁M = =CBM. Но ZCBM = ZABM, так как ВМ — биссектриса по условию. Тогда AB₁B = ABB₁ и АВВ₁ — равнобедренный по признаку равнобедренного треугольника. Следовательно, АВ=АВ₁. А так как АВ₁=ВС, то АВ = ВС. Теорема доказана.

Замечание. Прием продления (продолжения) медианы часто используется при решении геометрических задач.

Пример №7

В треугольнике ABC с периметром 54 см медиана АК перпендикулярна стороне ВС, а высота ВМ составляет равные углы со сторонами ВА и ВС. Найти стороны треугольника ABC.

Решение:

Так как медиана АК является и высотой, то АВС — равнобедренный с основанием ВС и АВ =АС. Так как высота ВМ является и биссектрисой, то АВС — равнобедренный с основанием АС и АВ = ВС. Тогда АВС — равносторонний, (см).

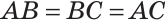
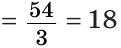
Пример №8

Биссектриса АК треугольника АБС делит сторону ВС пополам. Периметр треугольника ABC равен 36 см, периметр треугольника АКС равен 30 см. Найти длину биссектрисы АК.

Решение:

Из условия следует, что биссектриса АК является и медианой АВС (рис. 139).

Тогда АВС — равнобедренный по признаку равнобедренного треугольника и АВ=АС. Так как ВК = СК, то сумма отрезков АС и СК равна полупериметру АВС, то есть 18 см. По условию периметр АКС равен 30 см, поэтому АК = 30 — 18 = 12 (см).

Геометрия 3D

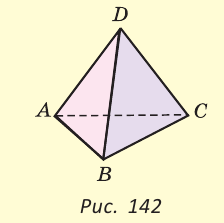
У правильной треугольной пирамиды DABC в основании лежит равносторонний треугольник ABC, а боковые грани ADB, ADC, BDC — равные равнобедренные треугольники с общей вершиной D (рис. 142).

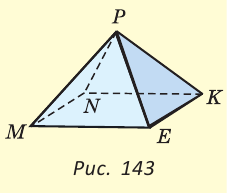
У правильной четырехугольной пирамиды в основании лежит квадрат MNKE, а боковые грани МРЕ, MPN, NPK, ЕРК — равные равнобедренные треугольники с общей вершиной Р (рис. 143).

Третий признак равенства треугольников

Вам уже известны два признака равенства треугольников. Рассмотрим еще один.

Теорема (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказать: АВС = А₁В₁С₁.

Доказательство:

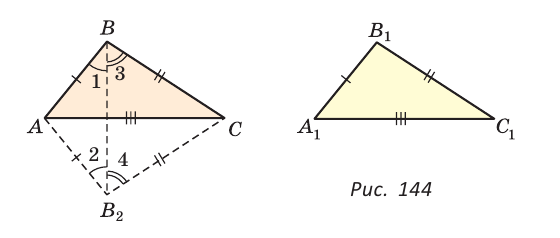
Приложим треугольник А₁В₁С₁ к треугольнику ABC так, чтобы у них совместились равные стороны А₁С₁ и АС, а вершины В₁ и В оказались в разных полуплоскостях относительно прямой АС. Треугольник А₁В₁С₁ займет положение треугольника АВ₂С. Проведем отрезок ВВ₂. Так как АВ₂=АВ и В₂С = ВС, то треугольники АВВ₂ и СВВ₂ — равнобедренные. Откуда l =2 и 3 =4 (как углы при основании равнобедренного треугольника). Тогда ABC =AB₂C, и треугольники ABC и АВ₂С равны по двум сторонам и углу между ними. Следовательно, АВС =А₁В₁С₁. Теорема доказана.

Замечание. Чтобы отрезок ВВ₂ проходил внутри треугольника ABC, следует прикладывать треугольники большей стороной.

Говорят, что три стороны задают треугольник однозначно.

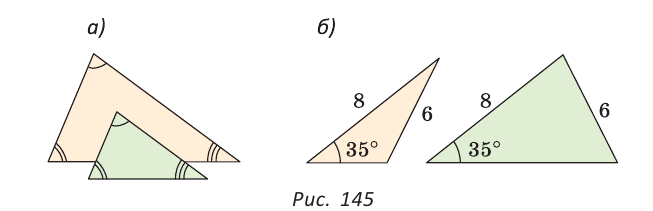
Итак, теперь вы знаете три признака равенства треугольников. Можно сформулировать и другие признаки равенства треугольников, в которых неизбежно будет присутствовать соответственное равенство каких-то трех элементов двух треугольников. Однако не любые три элемента задают треугольник. Так, например, если три угла одного треугольника соответственно равны трем углам другого треугольника, то такие треугольники не обязательно равны. То же касается треугольников, у которых соответственно равны две стороны и угол, противолежащий одной из этих сторон.

На рисунке 145, а, б вы видите пары таких неравных треугольников.

Пример №9

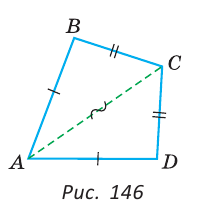
У простой замкнутой ломаной ABCD AB=AD, BC = DC. Доказать, что B = D и луч АС — биссектриса угла BAD.

Доказательство:

Проведем отрезок АС (рис. 146).

Треугольники ABC и ADC равны по 3-му признаку равенства треугольников (AB=AD и BC = DC по условию, сторона АС — общая). Поэтому B =D и BAC =DAC как соответствующие в двух равных треугольниках и луч АС — биссектриса угла BAD.

Пример №10

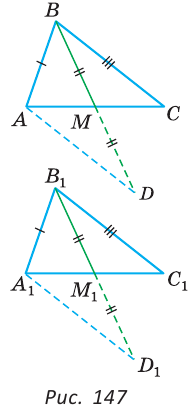
Доказать равенство треугольников по двум сторонам и медиане между ними.

Доказательство:

Нужно доказать, что АВС =А₁В₁С₁. Продлим в каждом треугольнике данную медиану на ее длину так, что MD = ВМ, M₁D₁=B₁M₁. Так как AMD =СМВ по 1-му признаку равенства треугольников (AM = МС, AMD =CMB как вертикальные, ВМ = MD по построению), то AD = BC. Аналогично AXMXDX = С₁М₁В₁, откуда A₁D₁ = B₁C₁. По условию ВС = В₁С₁, следовательно, AD=A₁D₁ и ABD =A₁B₁D₁ по трем сторонам. Тогда ABM =A₁B₁M₁ и АВМ =А₁В₁М₁ по 1-му признаку равенства треугольников. Отсюда AM =А₁М₁, АС =А₁С₁ (так как ВМ и В₁М₁ — медианы) и АВС =А₁В₁С₁ по трем сторонам.

Пример №11

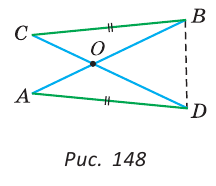
Два равных отрезка АВ и CD пересекаются в точке О и AD = BC. Доказать, что ВО = DO.

Доказательство:

Соединим точки В и D отрезком (рис. 148).

Треугольники ABD и CDB равны по трем сторонам (сторона BD — общая, AB=CD и AD=СВ по условию). Из равенства треугольников следует, что ABD =CDB. Тогда BOD — равнобедренный (по признаку равнобедренного треугольника), откуда ВО=DO.

Серединный перпендикуляр к отрезку

Определение. Серединным перпендикуляром к отрезку называется прямая, перпендикулярная этому отрезку и проходящая через его середину.

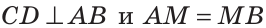
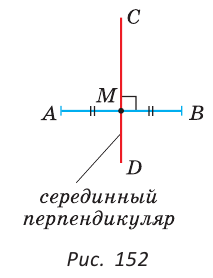
Прямая CD — серединный перпендикуляр к отрезку АВ, то есть (рис. 152).

Теорема (о серединном перпендикуляре).

Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.

В данной теореме два утверждения: прямое и ему обратное. Докажем каждое из этих утверждений отдельно.

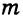
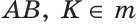
1) Дано: — серединный перпендикуляр к отрезку (рис. 153).

Доказательство:

По определению серединного перпендикуляра 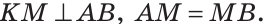Тогда в треугольнике АКВ высота КМ является медианой. По признаку равнобедренного треугольника АКВ — равнобедренный, поэтому КА=КВ.

2) Дано: 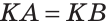(рис. 154).

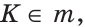
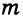
Доказать: где — серединный перпендикуляр к отрезку АВ.

Доказательство:

Проведем в равнобедренном АКВ высоту КМ, которая по свойству равнобедренного треугольника будет и медианой. Получим Прямая , проходящая через высоту КМ, — серединный перпендикуляр к отрезку АВ.

Геометрическим местом точек плоскости (или пространства) называется множество всех точек плоскости (или пространства), обладающих общим свойством.

Из доказанной теоремы следует, что серединный перпендикуляр к отрезку — это геометрическое место точек плоскости, равноудаленных от концов отрезка.

Пример №12

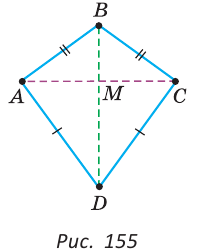
В четырехугольнике (рис. 155) ABCD AB=BC, AD=DC.

Доказать, что AC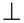BD.

Доказательство:

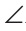
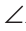
1-й способ. Из равенства треугольников ABD и CBD по трем сторонам следует, что ABD =CBD. В равнобедренном треугольнике ABC биссектриса ВМ является и высотой. Поэтому ACBD.

2-й способ. Точки В и D равноудалены от концов отрезка АС, поэтому они лежат на серединном перпендикуляре к отрезку АС. Так как через две точки проходит единственная прямая, то BD — серединный перпендикуляр к отрезку АС. Отсюда ACBD. и AM = МС.

Пример №13 (1-я замечательная точка треугольника).

Доказать, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство:

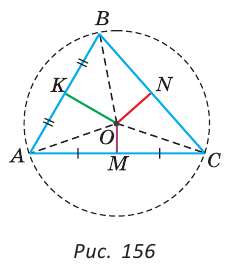
Пусть два серединных перпендикуляра к сторонам АС и АВ пересекаются в точке О (рис. 156).

Точка О лежит на серединном перпендикуляре ОМ, поэтому ОА = ОС. Точка О лежит на серединном перпендикуляре ОК, поэтому ОА = ОВ. Отсюда ОВ = ОС. Поскольку точка О равноудалена от концов отрезка ВС, то она лежит на серединном перпендикуляре к отрезку ВС. Таким образом, третий серединный перпендикуляр пройдет через точку О, и все три серединных перпендикуляра к сторонам треугольника пересекутся в одной точке.

• 1. Если ножку циркуля поставить в точку О и построить окружность радиусом OA, то она пройдет через все вершины треугольника в силу того, что OA = OB = ОС. Такая окружность называется описанной около треугольника. В данной задаче мы доказали, что центр окружности, описанной около треугольника, лежит в точке пересечения серединных перпендикуляров к его сторонам.
• 2. Точка пересечения серединных перпендикуляров к сторонам треугольника — это еще одна замечательная точка треугольника помимо уже известных вам точек пересечения биссектрис, медиан, высот.

Напомню:

Три признака равенства треугольников:

• По двум сторонам и углу между ними.
• По стороне и двум прилежащим к ней углам.
• По трем сторонам.

1. Углы при основании равнобедренного треугольника равны.
2. Биссектриса равнобедренного треугольника, проведенная из вершины к основанию, является его высотой и медианой.
3. Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника).
4. Если высота треугольника является его медианой или биссектрисой, или медиана является его биссектрисой, то треугольник равнобедренный (признаки равнобедренного треугольника).
5. Любая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Если точка равноудалена от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
6. Все три серединных перпендикуляра к сторонам треугольника пересекаются в одной точке (1-я замечательная точка треугольника).

• Признаки равенства прямоугольных треугольников
• Соотношения в прямоугольном треугольнике
• Сумма углов треугольника
• Внешний угол треугольника
• Задачи на построение циркулем и линейкой
• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

3) А) Обоснуйте равенство треугольников BAC и DCA, изображенных на рисунке,

3) А) Обоснуйте равенство треугольников BAC и DCA, изображенных на рисунке, если AD = CB и

• Ромихина Ленка
• Алгебра 2019-08-30 10:02:20 3 1

1) АD=CB по условию
2) lt;1=lt;2 по условию
3) АС — общая сторона
Следовательно, треугольники одинаковы по первому признаку равенства треугольников (
по двум граням и углу между ними)

Б)
В одинаковых треугольниках соответствующые элементы равны, потому угол АDC равен углу ABС.
Т.е
lt;АDC= 98

В равных треугольниках против одинаковых углов лежат одинаковые стороны.
Потому сторона АВ одинакова стороне CD
Т.е
АВ=СD= 28см
АВ= 28см

📸 Видео

Геометрия 7 класс (Урок№15 - Решение задач на признаки равенства треугольников.)Скачать

Признаки равенства треугольников. 7 класс.Скачать

Геометрия. 7 класс. Теоремы. Т3. Первый признак равенства треугольников.Скачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Задачи. Второй признак равенства треугольников. По рисункам. Доказать.Скачать

Первый признак равенства треугольников. 7 класс.Скачать

Признаки равенства треугольников. Практическая часть. 7 класс.Скачать

Второй признак равенства треугольников. 7 класс.Скачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Геометрия 7 класс (Урок№10 - Первый признак равенства треугольников.)Скачать

Геометрия 7 класс (Урок№14 - Второй и третий признаки равенства треугольников.)Скачать

ТРИ ПРИЗНАКА РАВЕНСТВА ТРЕУГОЛЬНИКОВ НА ЕГЭ #shorts #математика #егэ #огэ #профильныйегэ #геометрияСкачать

7 класс, 20 урок, Третий признак равенства треугольниковСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Задачи на доказательство равенства треугольников. Первый признак. Простые.Скачать

Треугольник. Равенство треугольниковСкачать

7 класс, 19 урок, Второй признак равенства треугольниковСкачать