- Дидактические материалы по теме «Параллельность в пространстве»
- 10 класс. Задачи для подготовки к контрольной работе N 4
- Плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b — в точках С и D. Каково взаимное
- Ваш ответ
- решение вопроса
- Похожие вопросы
- 🎥 Видео
Видео:№63. Параллельные плоскости a и β пересекают сторону АВ угла ВАС соответственно в точках A1 и A2Скачать
Дидактические материалы по теме «Параллельность в пространстве»
3.07. Точки А, В и С лежат в плоскости α и не лежат на одной прямой. Равные и параллельные отрезки АА1, ВВ1 и СС1 расположены по одну сторону от плоскости α. Докажите, что (А1В1С1) || 
(АВС) (рис. 38).
Решение: ВВ1С1С – параллелограмм (из параллельности и равенства ВВ1 и СС1), следовательно ВС || В1С1. АВ || А1В1 (аналогично). По теореме о параллельности плоскостей (по двум пересекающимся прямым): (А1В1С1) || (АВС).
3.08. Точка В не лежит в плоскости ΔAEC, точки М, К и Р – середины отрезков соответственно АВ, ВС и ВЕ (рис.39). а) Докажите, что плоскости МКР и АЕС параллельны. б) Найдите площадь ΔМКР, если площадь ΔAEC равна 48 см2.
Решение: а)Заметим, что ΔAEC и не лежащая в нем точка В образуют тетраэдр ВАСЕ. МК || АС (МК – средняя линия ΔAВC). КР || СЕ (КР – средняя линия ΔВCЕ). По теореме о параллельности плоскостей (через пересекающиеся прямые): (МКР)||(АСЕ).
б) По формуле Герона:
, как средние линии соответствующих треугольников. Подставим данные значения в формулу: 
. Отсюда 
.
3.09. Три отрезка А1А2, В1В2 и С1С2, не лежащие в одной плоскости, имеют общую середину. Докажите, что плоскости А1В1С1 и А2В2С2 параллельны (рис. 40).
Решение: Каждые две пересекающиеся прямые задают плоскость (через любые две пересекающиеся прямые можно провести плоскость, и притом только одну). Так как точка пересечения делит прямые пополам, то по теореме Фалеса: А1В1 || В2А2. Аналогично доказывается параллельность С1В1 и С2В2, А1В1 и А2В2. По теореме о параллельности плоскостей (через пересекающиеся прямые): (А1В1С1)||(А2В2С2).
3.10. Прямая DF пересекает параллельные плоскости α, β и γ соответственно в точках D, Е и F, при этом DF = 3, ЕF = 9 (рис. 41). Прямая EG пересекает плоскости α и γ соответственно в точках G и Н, при этом EG = 12. Найдите длину GН.
Решение: Прямые EF и ЕH задают плоскость EFH, которая пересекает плоскости α и γ по прямым GD и FH соответственно. ∆GED
∆HEF (так как GD || FH, 
). По свойству преобразования подобия: 
. Тогда 
.
3.11. Плоскости α и β пересекаются по прямой с (рис. 42). Через точки А и В, расположенные вне этих плоскостей, проводятся параллельно плоскости β и параллельные между собой прямые АС и BD (
), а также – параллельно плоскости α и параллельные между собой прямые АЕ и BF (
). Докажите: а) плоскости АСЕ и BDF параллельны; б) плоскости АСЕ и BDF пересекают плоскости α и β по параллельным прямым.
Решение: а) GА || DB, АЕ || FВ по условию. По теореме о параллельности плоскостей (через пересекающиеся прямые): (АСЕ) || (DBF).
б) BF и АЕ задают плоскость, параллельную плоскости α. По свойству параллельных плоскостей: EF || с. Аналогично CD || c. По признаку параллельности прямых: CD || EF.
5.3. Уроки проверки знаний, умений и навыков
Для проверки знаний, умений и навыков разработаны три задачи на выявление типов оперирования пространственными образами: изменение пространственного положения образа (I тип); преобразование структуры образа (II тип); изменение положения и структуры образа одновременно (III тип).
1. Через вершины параллелограмма ABCD, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А1, В1, С1 и D1. Докажите, что четырехугольник А1В1С1D1 тоже параллелограмм (рис. 43).
Решение: АА1 = DD1 = СС1 = ВВ1 (отрезки параллельных прямых, заключенные между параллельными плоскостями, равны). Попарно параллельные прямые задают параллелограммы (задание плоскости через параллельные прямые), следовательно D1А1 || DА || СВ || С1В1. По определению А1В1С1D1 параллелограмм.
Видео:10 класс, 10 урок, Параллельные плоскостиСкачать
10 класс. Задачи для подготовки к контрольной работе N 4
10 класс. Задачи для подготовки к контрольной работе N 4.
Угол между прямой и плоскостью. Параллельные плоскости
Отрезок AC – ортогональная проекция наклонной AB на плоскость ACD. Угол между лучами AC и AD равен 45 градусам. Найдите угол между лучами AB и AD, если угол между прямой AB и плоскостью ACD равен 60 градусам. Сторона AB прямоугольника ABCD лежит в плоскости ABM, a сторона BC образует с этой плоскостью угол 
. Какой угол образует диагональ BD с плоскостью ABM, если: а) BD = 2 AB, б) BC = 2 AB? Плоскости 
и 
параллельны, плоскость 
пересекает плоскость по прямой a, a плоскость — по прямой b. Плоскость 
пересекает плоскость по прямой c. Как могут быть расположены прямые a, b, c? Прямая DF пересекает параллельные плоскости , , соответственно в точках D, E, F, при этом DF = 3, FE = 9. Прямая EG пересекает плоскости и соответственно в точках G и H, при этом EG = 12. Найдите все значения, которые может принимать длина отрезка GH.
10 класс. Задачи для подготовки к контрольной работе N 4.
Угол между прямой и плоскостью. Параллельные плоскости
Отрезок AC – ортогональная проекция наклонной AB на плоскость ACD. Угол между лучами AC и AD равен 45 градусам. Найдите угол между лучами AB и AD, если угол между прямой AB и плоскостью ACD равен 60 градусам. Сторона AB прямоугольника ABCD лежит в плоскости ABM, a сторона BC образует с этой плоскостью угол . Какой угол образует диагональ BD с плоскостью ABM, если: а) BD = 2 AB, б) BC = 2 AB? Плоскости и параллельны, плоскость пересекает плоскость по прямой a, a плоскость — по прямой b. Плоскость пересекает плоскость по прямой c. Как могут быть расположены прямые a, b, c? Прямая DF пересекает параллельные плоскости , , соответственно в точках D, E, F, при этом DF = 3, FE = 9. Прямая EG пересекает плоскости и соответственно в точках G и H, при этом EG = 12. Найдите все значения, которые может принимать длина отрезка GH.
10 класс. Задачи для подготовки к контрольной работе N 4.
Угол между прямой и плоскостью. Параллельные плоскости
Отрезок AC – ортогональная проекция наклонной AB на плоскость ACD. Угол между лучами AC и AD равен 45 градусам. Найдите угол между лучами AB и AD, если угол между прямой AB и плоскостью ACD равен 60 градусам. Сторона AB прямоугольника ABCD лежит в плоскости ABM, a сторона BC образует с этой плоскостью угол . Какой угол образует диагональ BD с плоскостью ABM, если: а) BD = 2 AB, б) BC = 2 AB? Плоскости и параллельны, плоскость пересекает плоскость по прямой a, a плоскость — по прямой b. Плоскость пересекает плоскость по прямой c. Как могут быть расположены прямые a, b, c? Прямая DF пересекает параллельные плоскости , , соответственно в точках D, E, F, при этом DF = 3, FE = 9. Прямая EG пересекает плоскости и соответственно в точках G и H, при этом EG = 12. Найдите все значения, которые может принимать длина отрезка GH.
Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать
Плоскости α и β параллельны. Прямая а пересекает плоскости α и β соответственно в точках А и В, а прямая b — в точках С и D. Каково взаимное
Видео:Параллельность прямой и плоскости. 10 класс.Скачать
Ваш ответ
Видео:Параллельные прямые | Математика | TutorOnlineСкачать
решение вопроса
Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,680
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🎥 Видео
Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать
Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать
ПАРАЛЛЕЛЬНЫЕ ПЛОСКОСТИ 10 класс стереометрияСкачать
Геометрия 10 класс : Параллельные плоскости и их свойстваСкачать
10 класс, 11 урок, Свойства параллельных плоскостейСкачать
№51. Докажите, что плоскости α и β параллельны, если две пересекающиеся прямые mСкачать
№99. Докажите, что три параллельные плоскости отсекают на любых двух пересекающих эти плоскостиСкачать
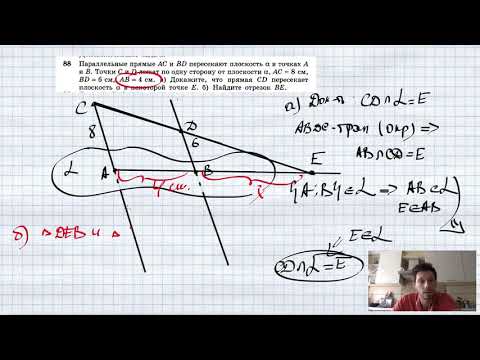
№88. Параллельные прямые АС и BD пересекают плоскость α соответственно в точках А и В. Точки С и DСкачать
№58. Докажите, что если плоскость γ пересекает одну из параллельных плоскостей α и β,Скачать
10. Параллельные плоскостиСкачать
№88. Параллельные прямые АС и BD пересекают плоскость α соответственно в точках А и В. Точки С и DСкачать
№49. Прямая m пересекает плоскость α в точке В. Существует ли плоскость, проходящая черезСкачать
10 класс, 6 урок, Параллельность прямой и плоскостиСкачать
№55. Докажите, что если прямая а пересекает плоскость α, то она пересекает также любуюСкачать
