Проведем окружность произвольного радиуса с центром в вершине а (8 видео)

Объясните, как отложить от данного луча угол, равный данному

—>Просмотров : 8946 | —>Добавил : V_V (07.11.2018) (Изменено: 07.11.2018)

Всего ответов: 3

Содержание

Провести окружность произвольного радиуса
Геометрия 7 класс
§ 4. Задачи на построение
Окружность
Построения циркулем и линейкой
Примеры задач на построение
Построение угла, равного данному
Построение биссектрисы угла
Построение перпендикулярных прямых
Построение середины отрезка
Задачи
Ответы к задачам
🌟 Видео

Обсуждение вопроса:

2) В вершину угла поставить острие циркуля и провести окружность.

3) На луче так же провести окружность.

4) На угле, там где окружность пересекает «нижнюю» сторону угла, поставить циркуль и провести окружность, радиус которой равен расстоянию от этой точки до другой стороны угла.

5) На луче. Из места пересечения окружности и луча провести еще одну окружность, равную той, которую мы провели на угле во второй раз.

6) Через точку пересечения окружностей провести прямоую, соединяющую начало луча.

Мы получили угол, равный данному.

Проведем произвольную окружность с центром в вершине А данного угла. Пусть В и С — точки пересечения окружности со сторонами угла. Радиусом АВ проведем окружность с центром в точке О — начальной точке данного луча. Точку пересечения этой окружности с данным лучом обозначим С₁. Опишем окружность с центром С₁ и радиусом ВС. Точка В₁ пересечения двух окружностей лежит на стороне искомого угла. Это следует из равенства Δ ABC = Δ ОВ₁С₁ (третий признак равенства треугольников).

Видео:№676. Стороны угла А касаются окружности с центром О радиуса r. Найдите: а) ОА,Скачать

Провести окружность произвольного радиуса

Скачать
презентацию

Решение >>

С. А. В. Провести окружность произвольного радиуса с центром в вершине А.

Слайд 12 из презентации «Окружность 7 класс». Размер архива с презентацией 975 КБ.

Видео:Примеры задач на построение | Геометрия 7-9 класс #24 | ИнфоурокСкачать

Геометрия 7 класс

«Декартова система координат на плоскости» — Место в кинотеатре. Введение более простых обозначений в алгебру. Древнегреческий астроном Клавдий. Проект по алгебре. Координаты в жизни людей. Координатная плоскость. Система географических координат. Биография Рене Декарта. Декартова система координат на плоскости. Гиппарх. Названия координат. Клетка на игровом поле. Точка пересечения осей. Линия времени. Определите координаты точек. Плоскость, на которой задана декартова система координат.

«Решение задач на построение» — Угол А. Построение треугольника по стороне и двум прилежащим к ней углам. Посмотрим на расположение циркулей. Задачи на построение. Построение перпендикулярных прямых. Отрезок РО является биссектрисой, а значит, и медианой. Построение треугольника по трем сторонам. Построение биссектрисы угла. РМ медиана. Построение треугольника по двум сторонам и углу между ними. Построение перпендикулярных прямых.

««Угол» 7 класс» — Половина угла. Вертикальные углы равны. Геометрическая фигура. Прямым углом называется угол, который составляет 90. Углом называется геометрическая фигура. Угол, который составляет 90. Перпендикулярные прямые. Биссектрисой называется луч, который выходит из вершины угла. Сумма смежных углов равна 180. Прямые, которые не пересекаются. Прямые, которые пересекаются под углом 90. Задачи для устного счета.

«Треугольники» — Первый признак равенства треугольников. Стороны равны. Треугольники равны. В любом треугольнике медианы пересекаются в одной точке. Биссектриса. Любой треугольник имеет три высоты. Равнобедренный. Любой треугольник имеет три биссектрисы. Доказательства равенства треугольников. Приложим треугольник. Сторона и два прилежащих к ней угла. Любой треугольник имеет три медианы. Высота. Медианы. Классификация треугольников.

«Треугольники в природе» — Кельма бетонщика. Пирамиды. Эльбрус. Солдатский треугольник. Встречающая фигура. Шри-янтра-мандала. Сиднейский оперный театр. Печать Соломона. Созвездие. Буддийский храм. Треугольники в природе. Знаки дорожного движения. Бермудский треугольник. Журнальный столик.

««Задачи по геометрии» 7 класс» — Отрезок KN. ABD = 100. Отрезок FD. OD – биссектриса. Отрезок KE. Отрезок АD. Вертикальные углы. Начальные геометрические сведения. BOC = 23. OE – биссектриса. Углы. Отрезок DF. EDK = 36. Смежные углы. Измерение углов. Отрезок АС. Отрезок MP. ABC = 72. Отрезок AB. AOB = 55. AOB = 45. OC – биссектриса. Измерение отрезков.

Всего в теме «Геометрия 7 класс» 55 презентаций

Видео:ЗАДАЧИ НА ПОСТРОЕНИЕ. §22 геометрия 7 классСкачать

§ 4. Задачи на построение

Окружность

Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением. Мы уже встречались с определениями, например с определением угла, смежных углов, равнобедренного треугольника и т. д. Дадим определение ещё одной геометрической фигуры — окружности.

Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.

Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, — радиусом окружности (рис. 77). Из определения окружности следует, что все радиусы имеют одну и ту же длину.

Отрезок, соединяющий две точки окружности, называется её хордой. Хорда, проходящая через центр окружности, называется её диаметром.

На рисунке 78 отрезки АВ и EF — хорды окружности, отрезок CD — диаметр окружности. Очевидно, диаметр окружности в два раза больше её радиуса. Центр окружности является серединой любого диаметра.

Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности. На рисунке 79 ALB и АМВ — дуги, ограниченные точками А и В.

Для изображения окружности на чертеже пользуются циркулем (рис. 80).

Чтобы провести окружность на местности, можно воспользоваться верёвкой (рис. 81).

Часть плоскости, ограниченная окружностью, называется кругом (рис. 82).

Построения циркулем и линейкой

Мы уже имели дело с геометрическими построениями: проводили прямые, откладывали отрезки, равные данным, чертили углы, треугольники и другие фигуры. При этом мы пользовались масштабной линейкой, циркулем, транспортиром, чертёжным угольником.

Оказывается, что многие построения можно выполнить с помощью только циркуля и линейки без масштабных делений. Поэтому в геометрии специально выделяют те задачи на построение, которые решаются с помощью только этих двух инструментов.

Что можно делать с их помощью? Ясно, что линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки. С помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. Выполняя эти несложные операции, мы сможем решить много интересных задач на построение:

построить угол, равный данному;
через данную точку провести прямую, перпендикулярную к данной прямой;
разделить данный отрезок пополам и другие задачи.

Начнём с простой задачи.

На данном луче от его начала отложить отрезок, равный данному.

Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ (рис. 83, а). Затем циркулем построим окружность радиуса АВ с центром О (рис. 83, б). Эта окружность пересечёт луч ОС в некоторой точке D. Отрезок OD — искомый.

Примеры задач на построение

Видео:7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

Построение угла, равного данному

Отложить от данного луча угол, равный данному.

Данный угол с вершиной А и луч ОМ изображены на рисунке 84. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ.

Проведём окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. 85, а). Затем проведём окружность того же радиуса с центром в начете данного луча ОМ. Она пересекает луч в точке D (рис. 85, б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е. Докажем, что угол МОЕ — искомый.

Рассмотрим треугольники АВС и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. 85, б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE.

Следовательно, ΔАВС = ΔODE по трём сторонам. Поэтому ∠DOE = ∠BAC, т. е. построенный угол МОЕ равен данному углу А.

То же построение можно выполнить и на местности, если вместо циркуля воспользоваться верёвкой.

Видео:7 класс, 23 урок, Примеры задач на построениеСкачать

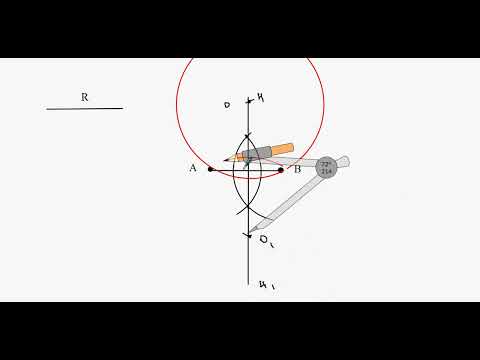
Построение биссектрисы угла

Построить биссектрису данного угла.

Данный угол ВАС изображён на рисунке 86. Проведём окружность произвольного радиуса с центром в вершине А. Она пересечёт стороны угла в точках В и С.

Затем проведём две окружности одинакового радиуса ВС с центрами в точках В и С (на рисунке изображены лишь части этих окружностей). Они пересекутся в двух точках, из которых хотя бы одна лежит внутри угла. Обозначим её буквой Е. Докажем, что луч АЕ является биссектрисой данного угла ВАС.

Рассмотрим треугольники АСЕ и АВЕ. Они равны по трём сторонам. В самом деле, АЕ — общая сторона; АС и АВ равны как радиусы одной и той же окружности; СЕ = BE по построению.

Из равенства треугольников АСЕ и АВЕ следует, что ∠CAE = ∠BAE, т. е. луч АЕ — биссектриса данного угла ВАС.

Можно ли с помощью циркуля и линейки разделить данный угол на два равных угла? Ясно, что можно, — для этого нужно провести биссектрису этого угла.

Данный угол можно разделить также на четыре равных угла. Для этого нужно разделить его пополам, а затем каждую половину разделить ещё раз пополам.

А можно ли с помощью циркуля и линейки разделить данный угол на три равных угла? Эта задача, получившая название задачи о трисекции угла, в течение многих веков привлекала внимание математиков. Лишь в XIX веке было доказано, что для произвольного угла такое построение невозможно.

Построение перпендикулярных прямых

Даны прямая и точка на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой.

Данная прямая а и данная точка М, принадлежащая этой прямой, изображены на рисунке 87.

На лучах прямой а, исходящих из точки М, отложим равные отрезки МА и МВ. Затем построим две окружности с центрами А и В радиуса АВ. Они пересекаются в двух точках: Р и Q.

Проведём прямую через точку М и одну из этих точек, например прямую МР (см. рис. 87), и докажем, что эта прямая — искомая, т. е. что она перпендикулярна к данной прямой а.

В самом деле, так как медиана РМ равнобедренного треугольника РАВ является также высотой, то PM ⊥ а.

Построение середины отрезка

Построить середину данного отрезка.

Пусть АВ — данный отрезок. Построим две окружности с центрами А и В радиуса АВ. Они пересекаются в точках Р и Q. Проведём прямую PQ. Точка О пересечения этой прямой с отрезком АВ и есть искомая середина отрезка АВ.

В самом деле, треугольники APQ и BPQ равны по трём сторонам, поэтому ∠1 =∠2 (рис. 89).

Следовательно, отрезок РО — биссектриса равнобедренного треугольника АРВ, а значит, и медиана, т. е. точка О — середина отрезка АВ.

Задачи

143. Какие из отрезков, изображённых на рисунке 90, являются: а) хордами окружности; б) диаметрами окружности; в) радиусами окружности?

144. Отрезки АВ и CD — диаметры окружности. Докажите, что: а) хорды BD и АС равны; б) хорды AD и ВС равны; в) ∠BAD = ∠BCD.

145. Отрезок МК — диаметр окружности с центром О, а МР и РК — равные хорды этой окружности. Найдите ∠POM.

146. Отрезки АВ и CD — диаметры окружности с центром О. Найдите периметр треугольника AOD, если известно, что СВ = 13 см, АВ = 16 см.

147. На окружности с центром О отмечены точки А и В так, что угол АОВ — прямой. Отрезок ВС — диаметр окружности. Докажите, что хорды АВ и АС равны.

148. На прямой даны две точки А и В. На продолжении луча В А отложите отрезок ВС так, чтобы ВС = 2АВ.

149. Даны прямая а, точка В, не лежащая на ней, и отрезок PQ. Постройте точку М на прямой а так, чтобы BM = PQ. Всегда ли задача имеет решение?

150. Даны окружность, точка А, не лежащая на ней, и отрезок PQ. Постройте точку М на окружности так, чтобы AM = PQ. Всегда ли задача имеет решение?

151. Даны острый угол ВАС и луч XY. Постройте угол YXZ так, чтобы ∠YXZ = 2∠BAC.

152. Дан тупой угол АОВ. Постройте луч ОХ так, чтобы углы ХОА и ХОВ были равными тупыми углами.

153. Даны прямая а и точка М, не лежащая на ней. Постройте прямую, проходящую через точку М и перпендикулярную к прямой а.

Построим окружность с центром в данной точке М, пересекающую данную прямую а в двух точках, которые обозначим буквами А и В (рис. 91). Затем построим две окружности с центрами А и В, проходящие через точку М. Эти окружности пересекаются в точке М и ещё в одной точке, которую обозначим буквой N. Проведём прямую MN и докажем, что эта прямая — искомая, т. е. она перпендикулярна к прямой а.

В самом деле, треугольники AMN и BMN равны по трём сторонам, поэтому ∠1 = ∠2. Отсюда следует, что отрезок МС (С — точка пересечения прямых а и MN) является биссектрисой равнобедренного треугольника АМВ, а значит, и высотой. Таким образом, MN ⊥ АВ, т. е. MN ⊥ а.

154. Дан треугольник АВС. Постройте: а) биссектрису АК; б) медиану ВМ; в) высоту СН треугольника. 155. С помощью циркуля и линейки постройте угол, равный: а) 45°; б) 22°30′.