В треугольнике авсд найдите ад

С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.

Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:

1. Три стороны треугольника.
2. Две стороны треугольника и угол между ними.
3. Две стороны и угол противостоящий к одному из этих сторон треугольника.
4. Одна сторона и любые два угла.

Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.

Видео:ЗАДАНИЕ 6 из ЕГЭ_6Скачать

Решение треугольника по трем сторонам

Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем .

(1)

(2)

Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

.

Пример 1. Известны стороны треугольника ABC: Найти (Рис.1).

Решение. Из формул (1) и (2) находим:

.

.

, .

И, наконец, находим угол C:

Видео:Задание 16 (В1) ОГЭ по математике ▶ №11 (Минутка ОГЭ)Скачать

Решение треугольника по двум сторонам и углу между ними

Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.

Найдем сторону c используя теорему косинусов:

.

.

Далее, из формулы

.

.

(3)

Далее из (3) с помощью калькулятора находим угол A.

Поскольку уже нам известны два угла то находим третий:

.

Пример 2. Известны две стороны треугольника ABC: и (Рис.2). Найти сторону c и углы A и B.

Решение. Иcпользуя теорму косинусов найдем сторону c:

,

.

Из формулы (3) найдем cosA:

.

Поскольку уже нам известны два угла то находим третий:

.

Видео:В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найти меньший угол треугольника ABCСкачать

Решение треугольника по стороне и любым двум углам

Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.

Так как, уже известны два угла, то можно найти третий:

.

Далее, для находждения сторон b и c воспользуемся тероемой синусов:

, .

, .

Пример 3. Известна одна сторона треугольника ABC: и углы (Рис.3). Найти стороны b и c и угол С.

Решение. Поскольку известны два угла, то легко можно найти третий угол С:

Найдем сторону b. Из теоремы синусов имеем:

Найдем сторону с. Из теоремы синусов имеем:

Видео:Задача 6 №27436 ЕГЭ по математике. Урок 50Скачать

ЕГЭ для VIP

Подготовке к ЕГЭ

Видео:№149. Отрезок AD перпендикулярен к плоскости равнобедренного треугольника ABC. Известно,Скачать

ЕГЭ по математике Профиль. Задание 3

ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

ЕГЭ Профиль. Задание № 3

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 3 рассчитано на умение использовать геометрические понятия и теоремы для решения практических задач, связанных с нахождением геометрических величин (длин, углов, площадей).

Задание состоит из текстовой задачи и рисунка. Необходимо внимательно прочитать текст, решить задачу и записать результат в поле ответа в тексте работы и бланк ответов. Если в итоге получилась обыкновенная дробь, её нужно перевести в десятичную.

Чтобы успешно справиться с данным заданием, нужно повторить определения и свойства плоских фигур:

• треугольники:
• четырёхугольники, в частности параллелограмм, прямоугольник, ромб, квадрат, трапеция;
• многоугольники, в частности правильные многоугольники;
• окружность и круг, описанные и вписанные в многоугольник окружности;
• площади треугольника, параллелограмма, трапеции, круга, сектора.

План выполнения:

1. Внимательно прочитайте задачу.
2. При необходимости выполните на чертеже дополнительные построения.
3. Выполните арифметические вычисления.
4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Задачи на Прямоугольные треугольники

При подготовке следует повторить значение синуса, косинуса и тангенса основных углов; отношения между сторонами прямоугольника; теорему Пифагора.

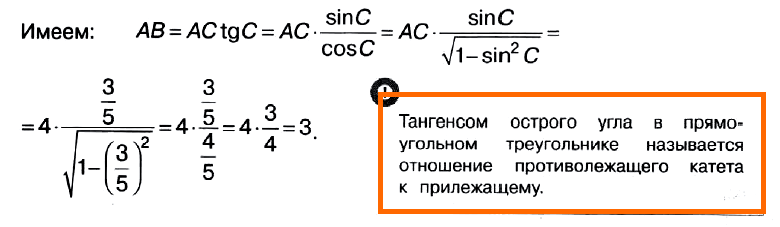
Задача № 3 (1). В треугольнике АВС угол А равен 90°, АС = 4, sin C = 3/5. Найдите АВ.

Решение:

Ответ: 3.

Задача № 3 (2). В треугольнике АВС угол С равен 90°, CD – высота, АВ = 5, tg B = 1/2. Найдите BD.

Решение: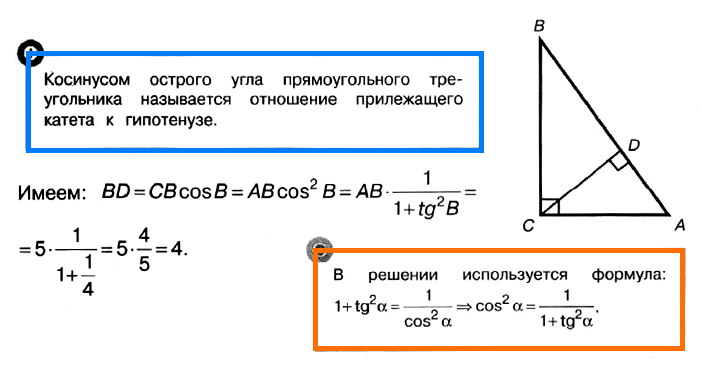

Ответ: 4.

Задачи на Равнобедренные треугольники

Задача № 3 (3). В треугольнике АВС АС = ВС = 10, sin А = 3/5. Найдите АВ.

Решение:

Ответ: 16.

Задача № 3 (4). В треугольнике АВС АС = ВС = 25, sin BAC = 3/5. Найдите высоту АН.

Решение:

Ответ: 24.

Задача № 3 (5). В тупоугольном треугольнике АВС АС = ВС = 6, высота АН = 3. Найдите sin АСВ.

Решение: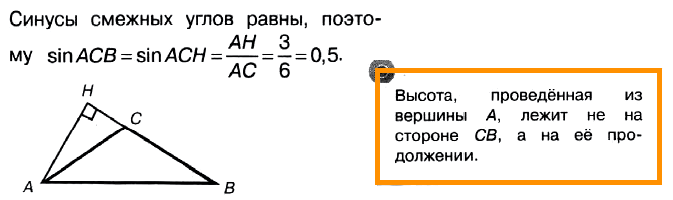

Ответ: 0,5.

Задачи на Разносторонние треугольники

Задача № 3 (6). Площадь треугольника АВС равна 8. DE — средняя линия CDE.

Решение:

Ответ: 2.

Задача № 3 (7). В треугольнике АВС угол С равен 60°, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.

Решение: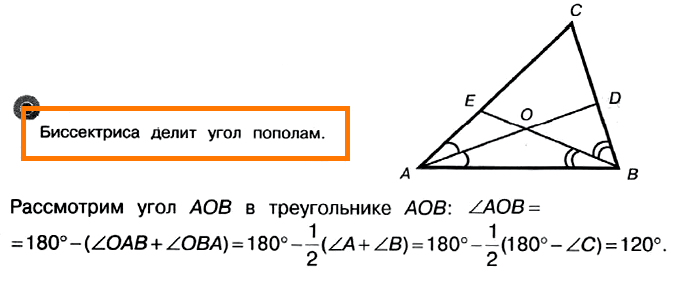

Ответ: 120.

Задачи на Параллелограммы

Задача № 3 (8). Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Решение: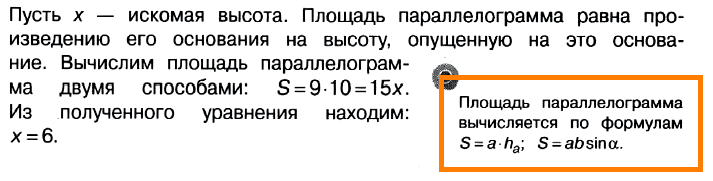

Ответ: 6.

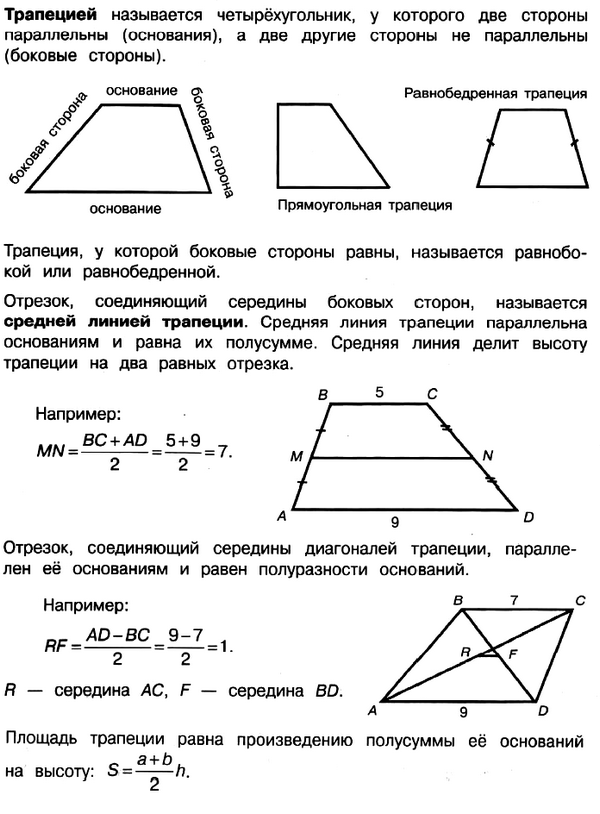
Задачи на Трапецию

Задача № 3 (9).

Решение: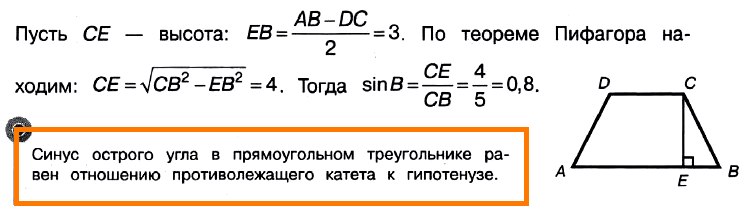

Ответ: 0,8.

Задачи на Центральные и вписанные углы

При подготовке нужно повторить свойства центральных и вписанных углов, понятия хорды, касательной и секущей к окружности; знать правила нахождения величин центральных и вписанных углов, дуг окружностей.

Задача № 3 (10). Найдите угол АСВ, если вписанные углы ADB и DAE опираются на дуги окружности, градусные величины которых равны соответственно 158° и 38°. Ответ дайте в градусах.

Решение:

Ответ: 60.

Задачи на Вписанные и описанные окружности

Задача № 3 (11). В четырёхугольник ABCD вписана окружность, АВ = 4, CD = 6. Найдите периметр четырёхугольника ABCD.

Решение:

Ответ: 20.

Задача № 3 (12).

Решение:

Ответ: 1.

Тренировочные задания с самопроверкой

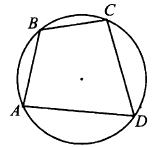
№ 3.1. Стороны АВ, ВС, CD и AD четырёхугольника ABCD стягивают дуги описанной окружности, градусные величины которых равны соответственно 75°, 63°, 93°, 129° (см. рис.). Найдите угол BCD. Ответ дайте в градусах.

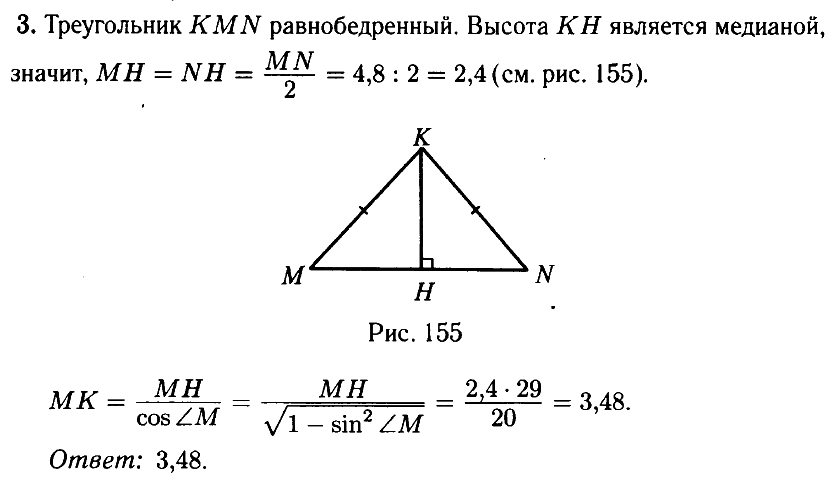
№ 3.2. В треугольнике MNK известно, что МК = NK, MN = 4,8, sin М = 21/29 (см. рис.). Найдите МК.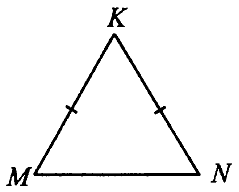

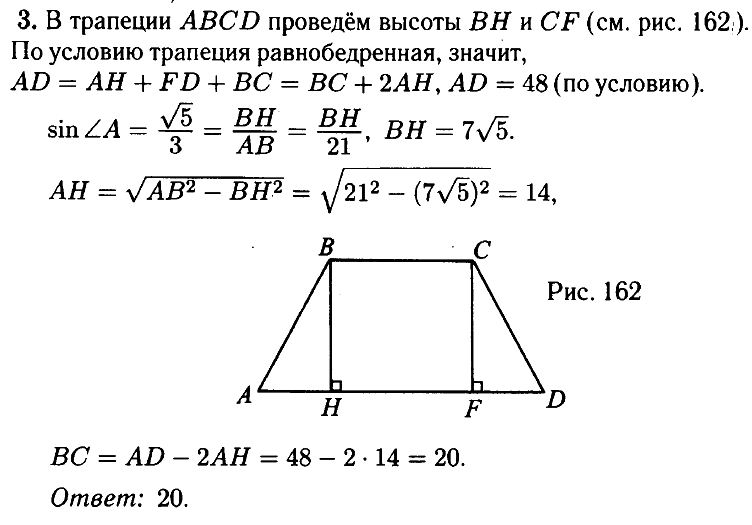
№ 3.3. Большее основание равнобедренной трапеции равно 48. Боковая сторона равна 21. Синус острого угла равен √5/3 (см. рис.). Найдите меньшее основание.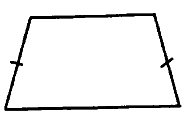

№ 3.4. В треугольнике АВС известно, что АС = ВС, высота ВН равна 9, АВ = 3√13 (см. рис.). Найдите tg АВС.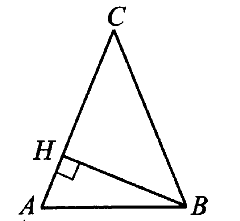

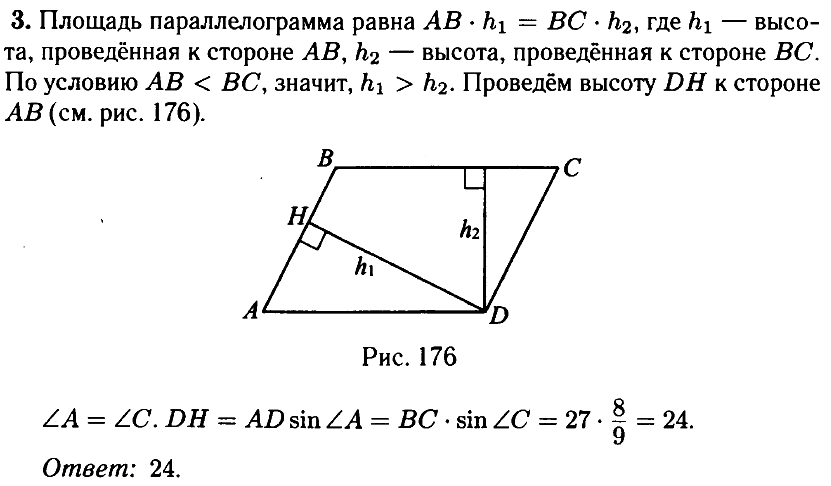
№ 3.5. В параллелограмме ABCD известно, что АВ = 18, ВС = 27, sin ∠C = 8/9 (см. рис.). Найдите большую высоту параллелограмма.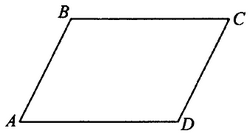

Вы смотрели: ЕГЭ по математике Профиль. Задание 3: Уметь выполнять действия с геометрическими фигурами, координатами и векторами. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Видео:25 задание ОГЭ ✧ В ∆ABC биссектриса BE и медиана AD перпендикулярны и ... #огэ #егэ #геометрияСкачать

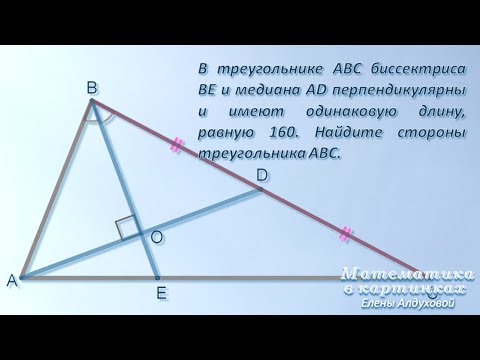
Решение №2327 В трапеции ABCD площадь равна 27, AD = 6, BC = 3. Найдите площадь треугольника ABC.

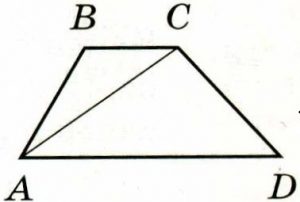
В трапеции ABCD площадь равна 27, AD = 6, BC = 3. Найдите площадь треугольника ABC.

Источник: Ященко ЕГЭ 2022 (30 вар).

Из формулы площади трапеции найдём высоту трапеции h:

|:9

h = 3·2 = 6

Высота трапеции одновременно является высотой ΔАВС, найдём площадь ΔАВС:

🎥 Видео

№235. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD. Найдите углыСкачать

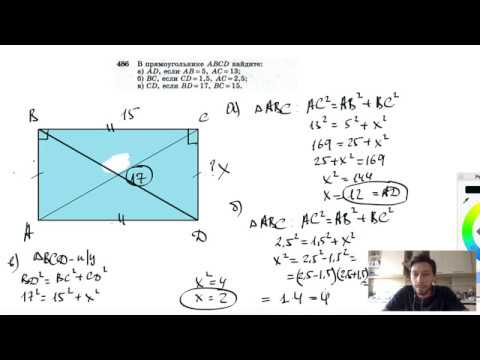
№486. В прямоугольнике ABCD найдите:Скачать

№537. Отрезок AD является биссектрисой треугольника ABC. Найдите BD и DC, если АВ = 14 смСкачать

№536. Отрезок BD является биссектрисой треугольника ABC. а) Найдите АВ, если ВС = 9 смСкачать

ОГЭ Р-2 номер 16Скачать

№538. Биссектриса AD треугольника ABC делит сторону ВС на отрезки CD и BD, равные соответственноСкачать

ОГЭ, задание #26, вариант-8Скачать

ОГЭ 2020 задание 16Скачать

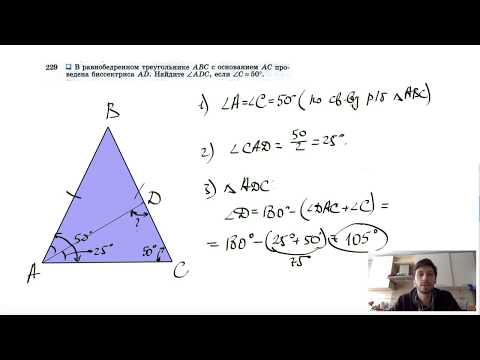
№229. В равнобедренном треугольнике ABC с основанием АС проведена биссектриса AD.Скачать

9 класс. Геометрия. ОГЭ. Окружность. Четырехугольники.Скачать

Точка E середина стороны AD параллелограмма ABCDСкачать

№448. На стороне AD прямоугольника ABCD построен треугольник ADE так, что его стороныСкачать

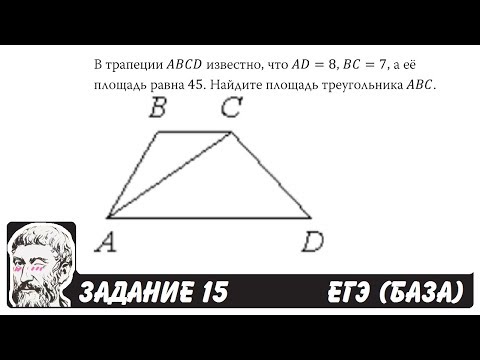
🔴 В трапеции ABCD известно, что AD=8, BC=7 ... | ЕГЭ БАЗА 2018 | ЗАДАНИЕ 15 | ШКОЛА ПИФАГОРАСкачать

В трапеции ABCD AB=CD, AC=AD и ∠ABC=95° ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать