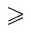Как построить треугольник равный данному

Видео:Построение угла равного данномуСкачать

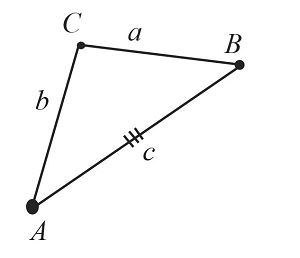
Как строить треугольник по 3 сторонам?

построение треугольника по трём сторонам.

1. Провести прямую.
2. На прямой от выбранной точки A отложить отрезок, равный данному отрезку a, и отметить другой конец отрезка B.
3. Провести окружность с центром A и радиусом, равным отрезку b.
4. Провести окружность с центром B и радиусом, равным отрезку c.

Видео:Построить угол , равный данному.Скачать

Как построить угол равный данному?

Чтобы построить угол равный данному, проводим прямую и ставим на ней точку. Это будет вершина нашего угла. Берем циркуль с произвольным раствором, ставим его на вершину данного угла. Проводим дугу таким образом, чтобы она пересекла лучи данного угла.

Видео:Построение треугольника, равного данномуСкачать

Можно ли построить треугольник по двум сторонам и медиане?

Отрезок, соединяющий вершину с серединой противоположной стороны, называют медианой. Зная длины двух сторон и медианы, соединяющихся в одной из вершин, можно построить треугольник, не имея данных о длине третьей стороны или величинах углов.

Видео:Построение угла равного данномуСкачать

Как построить прямоугольный треугольник по гипотенузе и катету?

По катету и гипотенузе прямоугольный треугольник можно построить как минимум двумя способами. Способ 1: Начертить прямую и отложить на ней меньший отрезок (обозначим его как AB). Для построения перпендикулярной прямой отложить такой же отрезок по другую сторону одной из точек концов отрезка, отложенного в п.

Видео:Построить угол равный данномуСкачать

Когда равны прямоугольные треугольники?

По гипотенузе и катету: если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

Видео:Построение треугольника по трем сторонам. 7 класс.Скачать

Как начертить отрезок с помощью циркуля и линейки?

Одно из решений показано на рисунке:

1. Циркулем проводим окружности с центром в точках A и B радиусом AB.
2. Находим точки пересечения P и Q двух построенных окружностей (дуг).
3. По линейке проводим отрезок или линию, проходящую через точки P и Q.
4. Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Видео:Построение угла, равного данномуСкачать

Как построить середину данного отрезка?

Для нахождения середины отрезка на плоскости можно сначала построить две дуги равного (и достаточно большого) радиуса с центрами в концах отрезка, а затем через точки пересечения этих дуг провести прямую. Точка, где полученная прямая пересекает отрезок, является его серединой.

Видео:Построение угла, равного данному. 7 класс.Скачать

Как рассчитать градус треугольника?

Если известны стороны треугольника, можно рассчитать его углы, воспользовавшись теоремой косинусов. Здесь, квадрат одной стороны треугольника (а) равен сумме квадратов двух его других сторон (b,с), образующих искомый угол (α), плюс удвоенное произведение этих сторон (b,с) на косинус угла.

Видео:Построить угол, равный данномуСкачать

Как сделать правильный треугольник?

Циркуль Проведите прямую линию. На лист бумаги положите линейку и проведите карандашом вдоль длинной стороны линейки. Полученный отрезок является первой стороной равностороннего треугольника, то есть вам нужно нарисовать еще две стороны той же длины, а каждый угол между сторонами должен быть равен 60 градусам.

Видео:Построение отрезка равного данномуСкачать

Как при помощи циркуля построить треугольник?

Построение правильного треугольника. Способ 1

1. Как построить равносторонний треугольник с помощью циркуля Шаг 1. Проведите отрезок АВ, длина которого равна а. .
2. Шаг 2. Возьмите циркуль. .
3. Шаг 3. Теперь неподвижную часть циркуля поставьте в точку В, а подвижную в точку А. .
4. Шаг 4. Окружности пересекаются в двух точках.

Видео:Аксиома существования треугольника, равного данномуСкачать

Задачи на построение циркулем и линейкой с примерами решения

Содержание:

Основные задачи на построение циркулем и линейкой:

В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.

При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:

1. с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
2. с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.

Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.

Видео:Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Задача 1 (построение угла, равного данному)

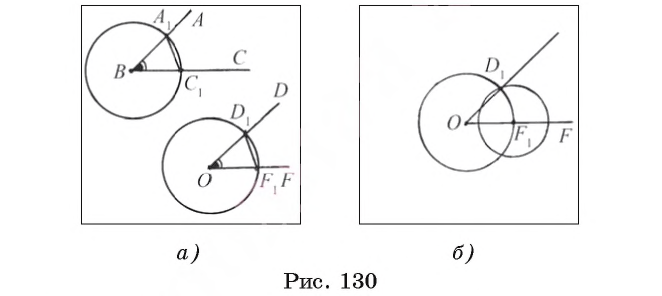
От данного луча OF отложите угол, равный данному углу ABC.

Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).

Пусть

1) Строим окружность (В, R) , где R — произвольный радиус, и отмечаем точки А₁ и С₁ пересечения ее со сторонами угла ABC.

2) Строим окружность 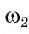(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F₁ с лучом OF.

3) Строим окружность (F₁, A₁C₁).

4) Пусть D₁ — одна из точек пересечения окружностей 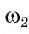(0, R) и (F₁, A₁C₁) (рис. 130, б). Тогда угол D₁OF — искомый. Докажем, что D₁OF =ABC.

Равенство D₁OF =ABC следует из равенства треугольников А₁ВС₁ и D₁OF₁. Действительно, по построению А₁В = D₁O = С₁В = F₁O. Кроме того, по построению F₁D₁ = А₁С₁, следовательно, треугольники А₁ВС₁ и D₁OF₁ равны по трем сторонам. Отсюда следует, что D₁OF =А₁ВС₁, т. е. построенный угол D₁OF равен данному углу ABC.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Задача 2 (построение серединного перпендикуляра к отрезку)

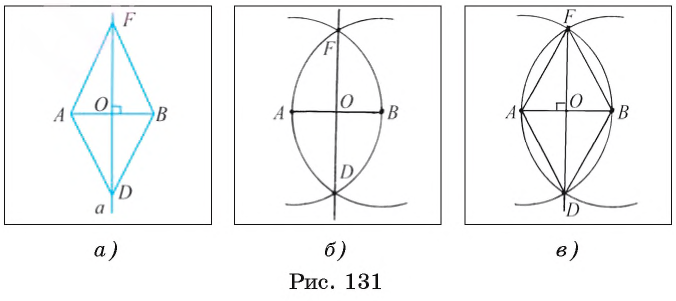
Постройте серединный перпендикуляр к данному отрезку АВ.

Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности (B, BF) и BF > ОВ. Аналогично AF =AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко увидеть, что AF = BF. Таким образом, точки F и D лежат также и на окружности (A, BF).

1) Строим окружности (A, R) и (B, R) , где R AВ. Пусть, например, R = AB: (A, AB) и (B, AB) (рис. 131, б).

2) Отмечаем точки F и D пересечения окружностей (A, AB) и (B, AB).

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.

Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, AFD = BFD. Отсюда следует, что в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, и высотой и медианой, т. е. прямая FO — серединный перпендикуляр к отрезку АВ.

Видео:Построить угол, равный данномуСкачать

Задача 3 (построение биссектрисы угла)

Постройте биссектрису данного угла ABC.

Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.

1) Строим окружность (B, R₁) произвольного радиуса R₁ с центром в вершине В данного угла (рис. 132, б).

2) Отмечаем точки F и D, в которых окружность (B, R) пересекает соответственно стороны ВА и ВС данного угла.

3) Строим окружности (F, R₂) и (D, R₂), где R2 > FD. Отмечаем точку Т их пересечения, которая лежит внутри данного угла.

4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.

Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что FBT = DBT, т. е. луч ВТ — биссектриса угла ABC.

Видео:Построение угла, равного данномуСкачать

Построение треугольника по трем элементам

В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.

Видео:Треугольники. 7 класс.Скачать

Задача 4 (построение треугольника по двум сторонам и углу между ними)

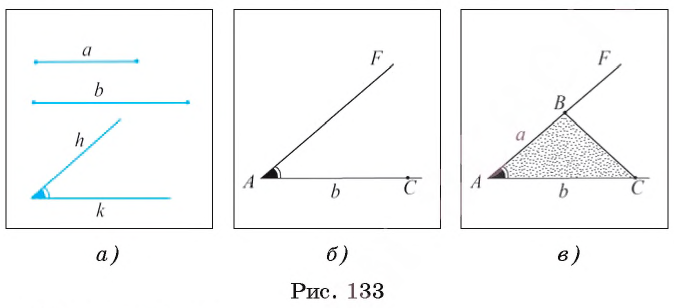
Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.

Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.

1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).

2) Строим угол CAF, равный углу hk.

3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).

По построению имеем, что АС = b, АВ = а и BAC = hk.

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.

Видео:Построение биссектрисы углаСкачать

Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)

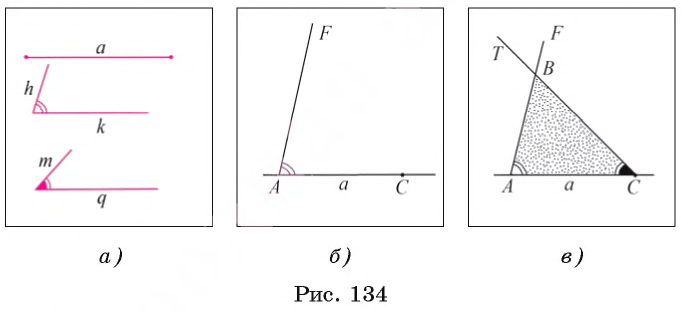
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.

Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.

1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).

2) Строим угол CAF, равный углу hk.

3) Строим угол ACT, равный углу mq.

4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).

По построению имеем, что АС = a, BAC = hk и ACB = mq.

Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.

Видео:Построение угла, равного данномуСкачать

Задача 6 (построение треугольника по трем сторонам)

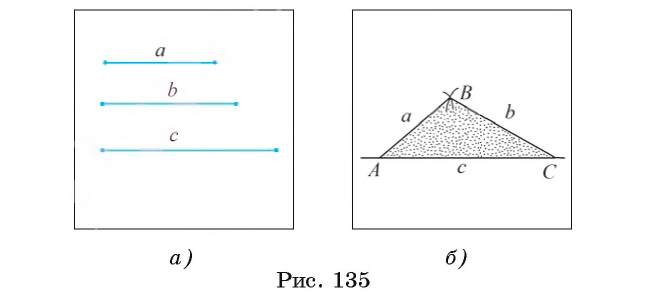
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.

Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.

1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).

2) Строим окружность (A, a).

3) Строим окружность (C, b).

4) Пусть В — одна из точек пересечения окружностей (A, a) и (C, b). Тогда треугольник ABC — искомый.

По построению АС = с, АВ = а, ВС = b.

Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.

• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Признаки равенства треугольников
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника — определение и вычисление
• Свойства прямоугольного треугольника
• Расстояние между параллельными прямыми

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Построение угла, равного данномуСкачать

Построение треугольников. Задачи на построение

Вы будете перенаправлены на Автор24

Решение задач на построение состоит из четырех основных этапов:

Каждый этап является важным. Например, анализ и исследование задачи необходимы для рассмотрения случаев, когда задача будет иметь решение, а когда – нет.

Построение фигур проще выполнять с помощью транспортира и линейки с делениями, но в математике необходимо уметь выполнять построение, используя циркуль и линейку без делений.

Видео:Постройте угол, равный данномуСкачать

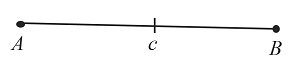
Построение отрезка, равного заданному

Построить отрезок, равный заданному, можно за 3 действия. Каждое действие обозначено на рисунке соответствующими цифрами.

Пусть необходимо построить отрезок, который будет равен отрезку $АВ$. Для этого:

1. Отметим произвольно точку $А_1$ и проведем луч с началом в этой точке.
2. С помощью циркуля измерим заданный отрезок $АВ$.
3. Проведем часть окружности с радиусом, равным отрезку $АВ$, и центром в точке $А_1$. В точке пересечения окружности и построенного луча получим точку $В_1$.

Таким образом, построенный отрезок $А_1 В_1$ будет равен заданному отрезку $АВ$.

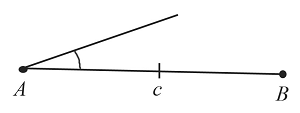
Построение угла, равного заданному

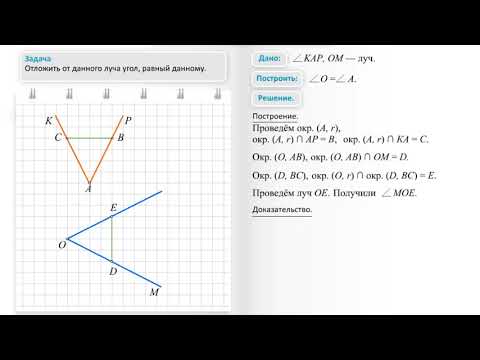
Построить угол, равный заданному, можно за $5$ действий. Каждое действие обозначено на рисунке соответствующими цифрами.

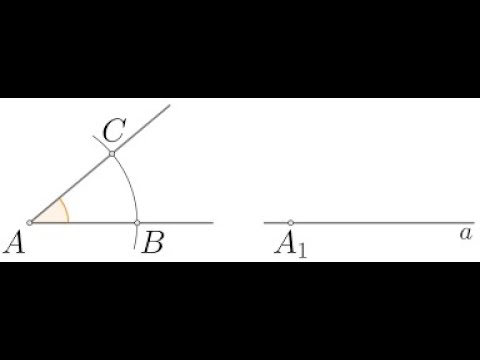
Пусть необходимо построить угол, который будет равен углу $А$.

1. Отметим произвольную точку $А_1$ и проведем из нее луч $А_1$.
2. Циркулем с произвольным радиусом проведем часть окружности с центром в точке $А$ до пересечения обеих сторон заданного угла $А$.
3. С тем же радиусом проведем часть окружности с центром в точке $А_1$ до пересечения с лучом $А_1$.
4. Из точек пересечения проведем окружности с одинаковым радиусом.
5. Проведем прямую из точки $А_1$ через вторую точку пересечения.

Готовые работы на аналогичную тему

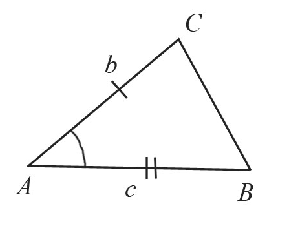
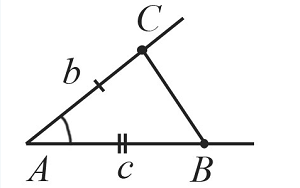
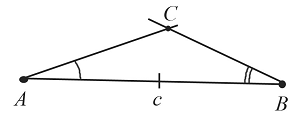
Построение треугольника по двум сторонам и углу между ними

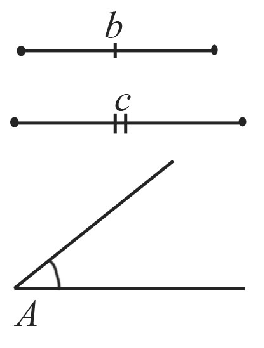
Пусть даны два отрезка $b$ и $с$ и угол $А$:

Необходимо построить треугольник с заданными двумя сторонами и углом между ними:

Построение выполняется в 4 этапа, каждый из которых показан на рисунках:

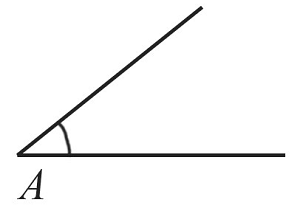
Построим угол $А$, который равен заданному углу по схеме, которая рассматривалась выше.

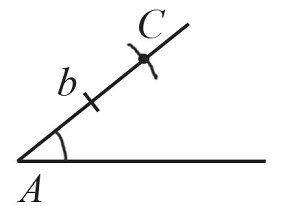
С помощью циркуля замеряем отрезок $b$ и отложим от точки $А$ такой же отрезок на одной из сторон построенного угла. Получим точку $С$.

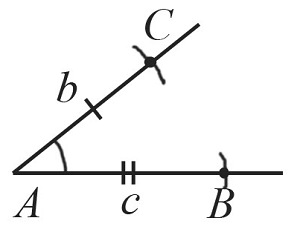
Циркулем замеряем отрезок $с$ и отложим от точки $А$ такой же отрезок на второй стороне построенного угла. Получим точку $В$.

С помощью линейки соединим точки $В$ и $С$.

Таким образом, получили треугольник $АВС$, построенный по двум сторонам и углу между ними.

Для облегчения построения полезно схематически изобразить будущий треугольник со всеми необходимыми элементами. Так будет наглядней видно, что после чего нужно строить.

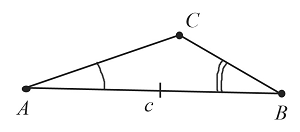
Построение треугольника по стороне и прилегающим к ней углам

Пусть даны два угла $А$ и $В$ и отрезок $с$:

Необходимо построить треугольник с заданными двумя углами и стороной, к которой они прилегают:

Построение выполняется в $3$ этапа, каждый из которых показан на рисунках:

Начертим произвольный отрезок $АВ$, который равен заданному отрезку $c$.

Построим угол $А$, который равен заданному, как показано выше.

Построим угол $В$, который равен заданному.

Точка пересечения двух сторон построенных углов $А$ и $В$ является вершиной треугольника $С$.

Таким образом, получили треугольник $АВС$, построенный по стороне и двум углам.

Построение треугольника по трем сторонам

Пусть даны $3$ отрезка $а$, $b$ и $с$.

Необходимо построить треугольник по трем заданным сторонам.

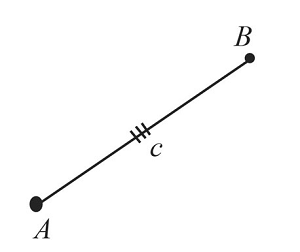
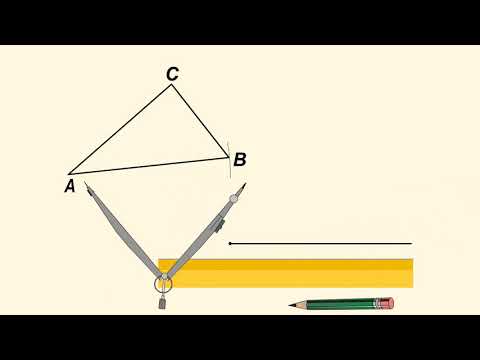
Построим отрезок $АВ$, который равен заданному отрезку $c$.

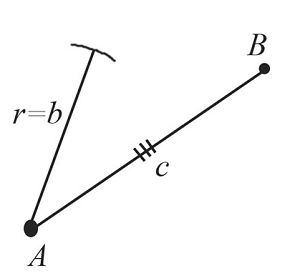
Из точки $А$ проведем часть окружности с радиусом, равным заданному отрезку $b$.

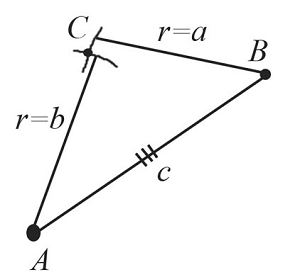
Из точки $В$ проведем часть окружности с радиусом, равным заданному отрезку $a$. Пересечением обеих окружностей является точка $С$.

Таким образом, получили построенный треугольник $АВС$ по трем заданным сторонам.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 22 07 2021