§ 12. Параллельное проектирование и его свойства.
В начале учебника на плоскости изображены некоторые фигуры, расположенные в пространстве. Эти изображения строились с целью придать наглядность тому, о чём шла речь в соответствующей теореме или задаче.
Однако изображения пространственных фигур на плоскости строятся по определённым правилам и в школьном курсе геометрии обычно осуществляются с помощью метода параллельного проектирования, сущность которого состоит в следующем.
В пространстве выбирается произвольная плоскость π Плоскость проекций в начертательной геометрии чаще всего обозначают π . , которую называют плоскостью проекций или плоскостью изображения , и прямая l , пересекающая эту плоскость (рис. 71, а ).
Пусть M ′ — произвольная точка пространства. Через эту точку проведём прямую p , параллельную l . Точка M пересечения прямой p с плоскостью π называется параллельной проекцией точки M ′ на плоскость π в направлении прямой l . Если M ′ — точка плоскости π , то M совпадает с M ′ .
При этом часто пользуются обозначением: M = П 
Прямую l и все прямые пространства, параллельные ей, называют проектирующими прямыми ; они определяют направление проектирования. Всякая плоскость пространства, параллельная проектирующей прямой, называется проектирующей плоскостью .
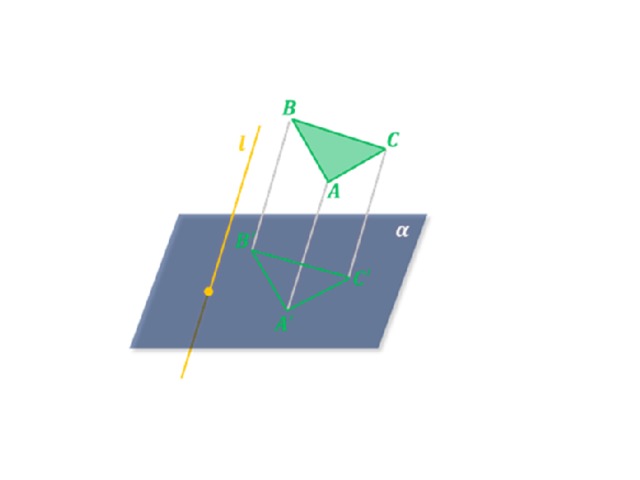
Фигура, которую проектируют или изображают, называется оригиналом. Для построения проекции фигуры достаточно построить проекции всех точек этой фигуры или проекции точек фигуры, её определяющих. На рисунке 71, б треугольник ABC является параллельной проекцией треугольника A ′ B ′ C ′ на плоскость π в направлении прямой l .
Замечание. Наряду с параллельным проектированием рассматривается также центральное проектирование фигур на плоскость. В этом случае проектирующие прямые проходят через одну точку — центр проектирования , произвольно выбранную вне плоскости проекций (рис. 71, в ).
Параллельное и центральное проектирование можно наблюдать в реальном пространстве: тень, которую отбрасывает предмет в солнечный день, является параллельной проекцией этого предмета, так как солнечные лучи можно считать приближённо параллельными вследствие большого удаления Солнца от Земли. А изображение на экране кинотеатра фигуры, заснятой на киноплёнку, является центральной проекцией этой фигуры.
На рисунках 72, 73, 74 изображены в параллельной проекции соответственно квадрат, треугольник и каркас тетраэдра. По этим рисункам можно сделать предположение, что ни величина угла, ни длина отрезка при параллельном проектировании, вообще говоря, не сохраняются.
Рассмотрим некоторые свойства параллельного проектирования.
1. Все точки проектирующей прямой проектируются в одну точку — точку пересечения этой прямой с плоскостью проекций (рис. 75).
В дальнейшем мы будем рассматривать проекции прямых, не параллельных проектирующим прямым.
2. Проекция прямой есть прямая. Действительно, все прямые, проектирующие точки данной прямой m ′ (рис. 76), принадлежат некоторой проектирующей плоскости, которая пересекает плоскость проекций по некоторой прямой m — параллельной проекции прямой m ′ .
Причём, так как через точку, не лежащую на данной прямой, можно провести лишь одну прямую, параллельную этой прямой (т. 6) (мы проводим прямые, параллельные прямой l ), то каждая точка прямой m ′ проектируется в единственную точку своей проекции — прямой m , и наоборот, каждая точка прямой m является проекцией единственной точки прямой m ′ .
Из доказательства этого свойства следует: три точки, лежащие на одной прямой, проектируются в три точки, также лежащие на одной прямой .

3. Две параллельные прямые проектируются либо в две параллельные прямые, либо в одну и ту же прямую. Действительно, если прямые a ′ и b ′ лежат в одной проектирующей плоскости, то они проектируются в одну и ту же прямую, а именно, в прямую, по которой эта проектирующая плоскость пересекает плоскость проекций.
Пусть теперь прямые a ′ и b ′ параллельны (рис. 77) и не лежат в одной проектирующей плоскости.
Обозначим через α и β плоскости, образованные прямыми, проектирующими точки прямых соответственно a ′ и b ′ . Прямые a и b , по которым плоскости α и β пересекают плоскость проекции, не могут пересекаться, так как если бы эти прямые имели общую точку M , то и прямые a ′ и b ′ по свойству 2 имели бы общую точку M ′ , что невозможно в силу параллельности прямых a ′ и b ′ . А так как прямые a и b лежат в одной плоскости (плоскости проекций) и не имеют общей точки, то они параллельны, т. е. параллельными проекциями параллельных прямых, не лежащих в одной проектирующей плоскости, являются параллельные прямые.
Заметим, что плоскости α и β , проектирующие параллельные прямые a ′ и b ′ , не лежащие в одной проектирующей плоскости, параллельны (в п. 9.1 показано, что параллельные плоскости существуют; о свойствах параллельных плоскостей речь пойдёт в следующей главе).
4. Проекции параллельных отрезков лежат либо на параллельных прямых, либо на одной прямой. Отношение длин отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин проекций этих отрезков.
Если отрезки A ′ B ′ и B ′ C ′ лежат на одной прямой a ′ и проектируются на отрезки соответственно AB и BC прямой a (рис. 78), то по обобщённой теореме Фалеса в плоскости, определяемой прямыми a и a ′ , получаем A ′ B ′ : B ′ C ′ = AB : BC = m : n .
Пусть теперь отрезки A ′ B ′ и C ′ D ′ расположены соответственно на данных параллельных прямых a ′ и b ′ , не лежащих в одной проектирующей плоскости, и A ′ B ′ : C ′ D ′ = m : n ; AB и CD , a и b — соответственно их параллельные проекции на плоскость π (рис. 79).
Так как a ′ ‖ b ′ , то (по свойству 3) a ‖ b . Пусть E — такая точка прямой a , что четырёхугольник BCDE — параллелограмм. Тогда на прямой a ′ существует (единственная!) такая точка E ′ , что E ′ E ‖ DD ′ и A ′ B ′ : B ′ E ′ = AB : BE . А так как BC ‖ ED , то B ′ C ′ ‖ E ′ D ′ (по свойству 3), значит, B ′ C ′ D ′ E ′ — параллелограмм. Поэтому A ′ B ′ : C ′ D ′ = A ′ B ′ : B ′ E ′ = AB : BE = AB : CD , т. е. A ′ B ′ : C ′ D ′ = AB : CD = m : n .
Из этого свойства, очень важного для теории построений изображений пространственных фигур на плоскости, следует не менее важный вывод: если отрезок A ′ C ′ параллельно проектируется на отрезок AC и точка B ′ делит отрезок A ′ C ′ в отношении A ′ B ′ : B ′ C ′ = m : n , то точка B — проекция точки B ′ — делит отрезок AC в том же отношении m : n , т. е. AB : BC = A ′ B ′ : B ′ C ′ = m : n . В частности, середина отрезка A ′ C ′ параллельно проектируется в середину отрезка AC ( m : n = 1 : 1) (рис. 80).
Пусть M — внутренняя точка отрезка AB .
Определение. Число λ , равное отношению длин отрезков AM и MB , на которые точка M делит отрезок AB , называется простым отношением трёх точек A , B и M , лежащих на одной прямой, и обозначается ( AB ; M ), т. е. ( AB ; M ) = λ = AM : MB .
При этом точки A и B называются базисными , а точка M — делящей точкой.
Упорядоченность точек простого отношения необходима. Например, если AA 1 — медиана треугольника ABC , M — его центроид (точка пересечения медиан треугольника), то ( AA 1 ; M ) = AM : MA 1 = 2 : 1, но ( A 1 A ; M ) = A 1 M : MA = 1 : 2 (рис. 81). Поэтому, если AM ≠ MA 1 , то
( AA 1 ; M ) ≠ ( A 1 A ; M ).
Учитывая свойство 4 параллельного проектирования, можно сделать вывод: простое отношение трёх точек, лежащих на одной прямой, при параллельном проектировании сохраняется . В этом случае также говорят, что простое отношение трёх точек, лежащих на одной прямой, — инвариант параллельного проектирования .
Свойства фигуры, сохраняющиеся при параллельном проектировании, называются аффинными свойствами этой фигуры. Например, свойства прямых быть параллельными — аффинное свойство этих прямых; инвариантность простого отношения трёх точек одной прямой — аффинное свойство таких точек.
Подробнее о параллельном проектировании и изображениях фигур на плоскости читайте в конце учебника.
Определение. Проектирование в направлении прямой, перпендикулярной плоскости проекций, называется ортогональным.
Удобно пользоваться обозначением: M = П 
Ортогональное проектирование является частным случаем параллельного и обладает всеми его свойствами. Однако, если при параллельном проектировании, не являющимся ортогональным, длина проекции отрезка может быть меньше, больше или равна длине самого отрезка, то при ортогональном проектировании длина проекции отрезка не больше, чем длина самого отрезка, и длины этих отрезков связаны соотношением: П 
Задания для работы с интернет-ресурсами
1. Наберите в поисковой системе слова «Перпендикулярность прямой и плоскости», «Перпендикуляр и наклонная к плоскости», «Наклонная и её проекция на плоскость», «Теорема о трёх перпендикулярах». На изображениях куба, параллелепипеда найдите рёбра и диагонали, перпендикулярные граням и сечениям этих многогранников. Найдите видеоролики с лекциями опытных педагогов и геометров, в которых выражаются различные взгляды как на теорию, так и на решение задач по этим вопросам.
2. Наберите в поисковой системе слова «угол между наклонной и плоскостью». Поищите задачи ЕГЭ типа С-2, в которых используется нахождение угла между прямой и плоскостью, посмотрите, как они решаются, попробуйте решить их самостоятельно. Если вам удалось найти в Интернете тренинг по решению задач этой темы, то попытайтесь им воспользоваться. Однако решать такие задачи целесообразнее после изучения темы «Расстояния в пространстве». Скоро вы изучите эту тему.
3. Изображения фигур на плоскости и в живописи подчиняются определённым законам. Найдите в Интернете такие имена, как Филиппо Брунеллески (1377—1446), Леонардо да Винчи (1452—1519) и Альбрехт Дюрер (1471—1528). Вы увидите творчество этих великих художников. Однако существует направление, которое называется импоссибилизм (impossibility — невозможность) — изображение невозможных фигур, парадоксов. Представителем этого направления живописи является известный голландский художник Мауриц Эшер (1898—1972). Найдите статьи, посвящённые его творчеству, а главное, найдите сами репродукции картин, которые представляют большой интерес и с точки зрения геометрии.
Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Параллельность в пространстве
в пространстве тоже бывают параллельные прямые. Но… не только прямые. Поскольку в пространстве вообще объектов больше, чем на плоскости, то и вариантов параллельностей тоже больше. Итак, в пространстве могут оказаться параллельными
2. Прямая и плоскость
3. Две плоскости.
Давай разберёмся с каждым вариантом.
1. Параллельность двух прямых в пространстве
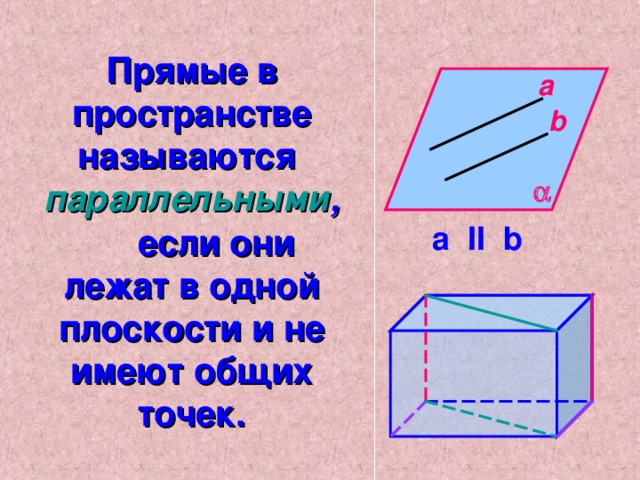
Прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Обрати внимание! Здесь очень важны слова «лежат в одной плоскости». Потому что в пространстве бывают другие, НЕ параллельные прямые, которые тоже НЕ пересекаются. Вот, например, такие:
Видишь, через прямые a и b никак нельзя провести плоскость, но они и не пересекаются. Такие прямые называются скрещивающиеся. Не пересекающиеся! И не параллельные!
Прямые в пространстве параллельны, если лежат в одной плоскости и не пересекаются.
2. Параллельность прямой и плоскости
Прямая и плоскость параллельны, если они не пересекаются, сколько бы их ни продолжали.
Просмотр содержимого документа
«Параллельность в пространстве»

Способы задания плоскостей
Изображение пространственных фигур на плоскости
Существование в пространстве
Возьмите две прямые ( ручки и т. д. ) и расположите их на плоскости ( столешнице парты ) так, чтобы они не имели общих точек; имели одну общую точку; имели множество общих точек.
Проделайте эту же работу, но располагайте прямые в пространстве .
С д е л а й т е в ы в о д
Сколько способов взаимного расположения прямых на плоскости и в пространстве существует?
- параллельными
- пересекающимися
- скрещивающимися
- совпадающими
Прямые в пространстве называются параллельными , если они лежат в одной плоскости и не имеют общих точек.

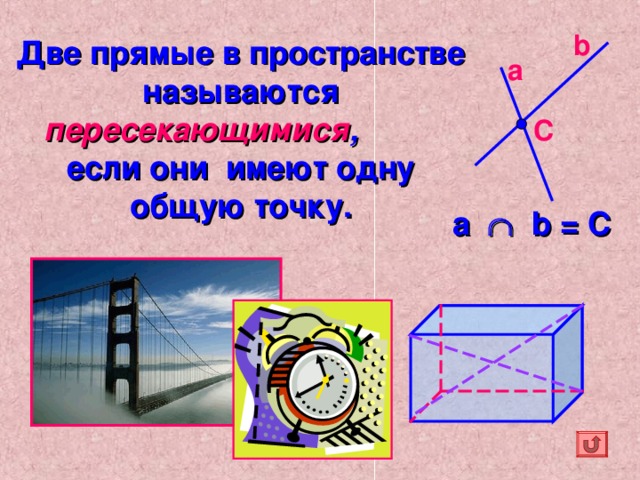
Две прямые в пространстве называются пересекающимися , если они имеют одну общую точку.
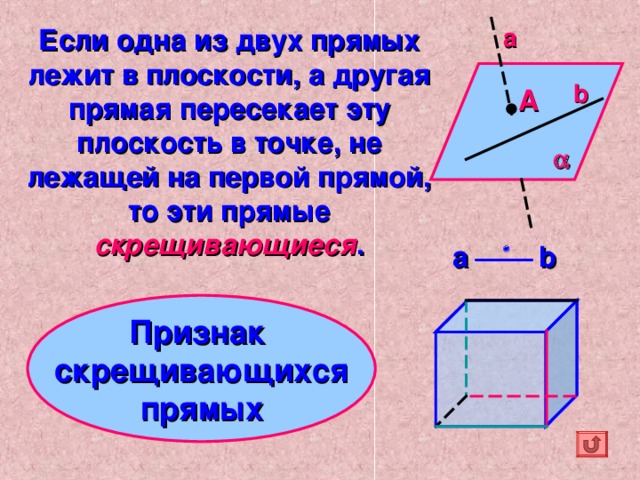
Две прямые в пространстве называются c крещивающимися , если они не лежат в одной плоскости и не имеют общих точек.
Если одна из двух прямых лежит в плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся .
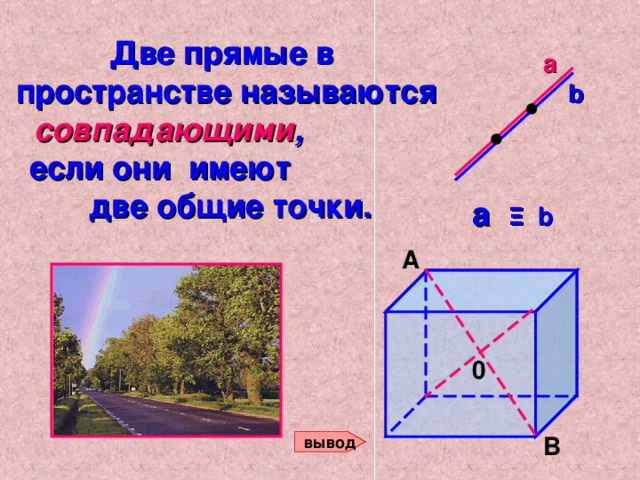
Две прямые в пространстве называются совпадающими , если они имеют две общие точки.
двух прямых в пространстве
Прямые не имеют
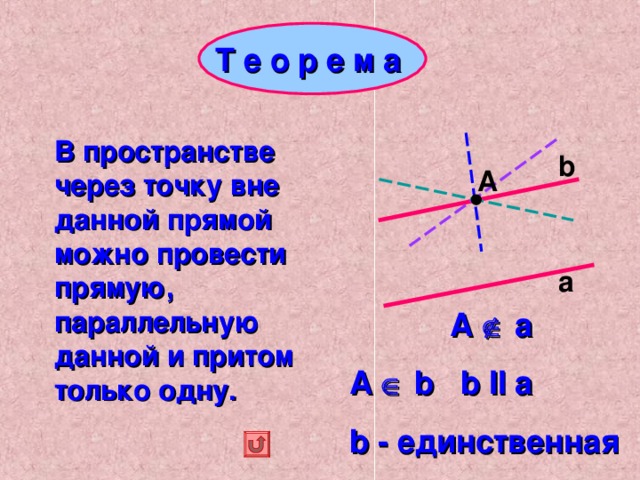
В пространстве через точку вне данной прямой можно провести прямую, параллельную данной и притом только одну.
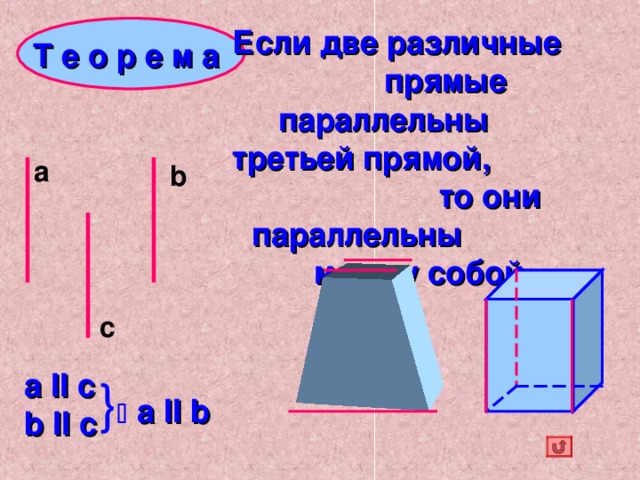
Если две различные прямые параллельны третьей прямой, то они параллельны между собой.
Возьмите прямую ( ручку или карандаш ) и расположите её так к плоскости ( столешнице парты ) , чтобы они были параллельными; были пересекающимися; прямая лежала в плоскости.
Сколько общих точек есть у прямой и плоскости в каждом случае?
С д е л а й т е в ы в о д
Дайте определение каждого из трёх случаев взаимного расположения прямой и плоскости.
- прямаяпараллельнаплоскости
- прямаяпересекаетплоскость
- прямаялежитна плоскости
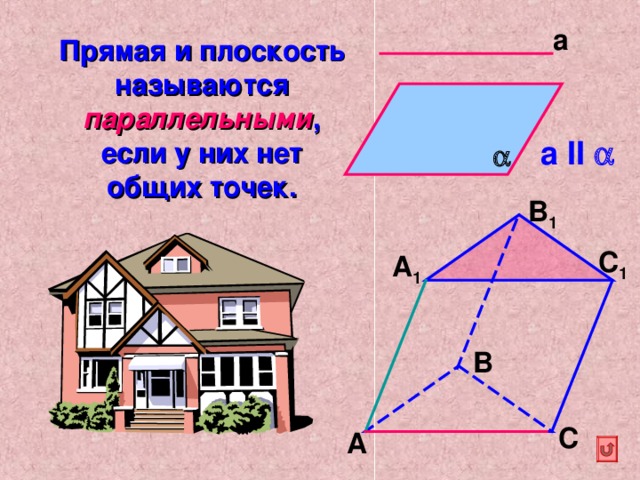
Прямая и плоскость называются параллельными , если у них нет общих точек.
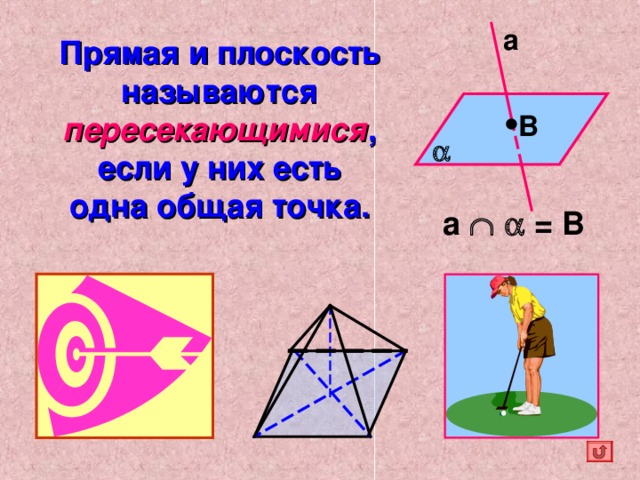
Прямая и плоскость называются пересекающимися , если у них есть одна общая точка.
Прямая лежит на плоскости , если у них есть две общие точки.
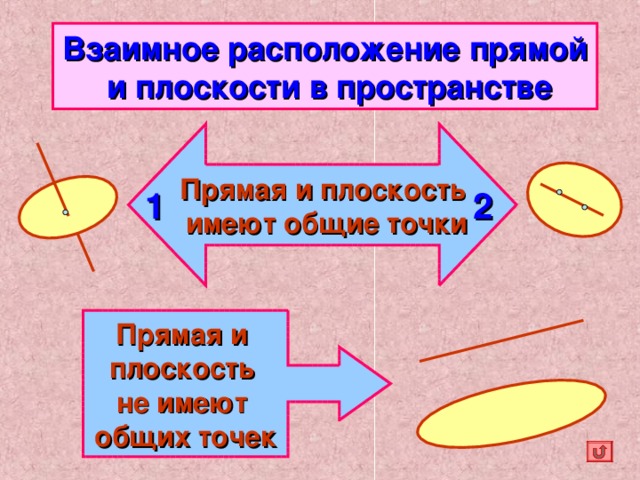
Взаимное расположение прямой
и плоскости в пространстве
Прямая и плоскость
имеют общие точки
Если прямая, не лежащая на плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельна данной плоскости.
Выделите условие и заключение теоремы.
С д е л а й т е в ы в о д
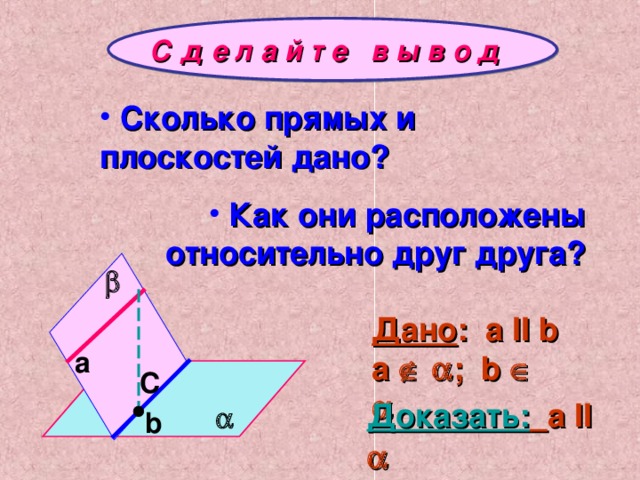
- Сколько прямых и плоскостей дано?
- Как они расположены относительно друг друга?
Составьте план доказательства
- Имея двепараллельныепрямые«а»и«b»можно провести ………
- ПустьаIIпрямая«a»и плоскость«»…………
- Точка пересечения«С»должна находиться на общей прямой плоскостей«»и«», то есть на….
- Получили: прямые«а»и«b»………
- Полученный результатне возможен, т. к.по условиюпрямые …………
Т е о р е м а 1
Если плоскость проходит через прямую, параллельную другой плоскости, и пересекает её, то линия пересечения плоскостей параллельна данной прямой.
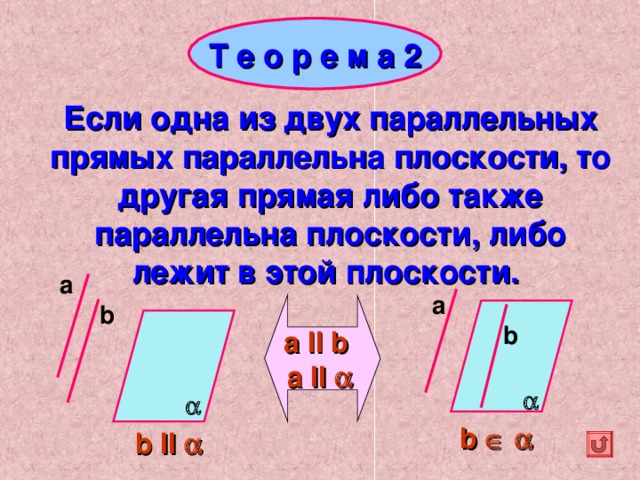
Т е о р е м а 2
Если одна из двух параллельных прямых параллельна плоскости, то другая прямая либо также параллельна плоскости, либо лежит в этой плоскости.
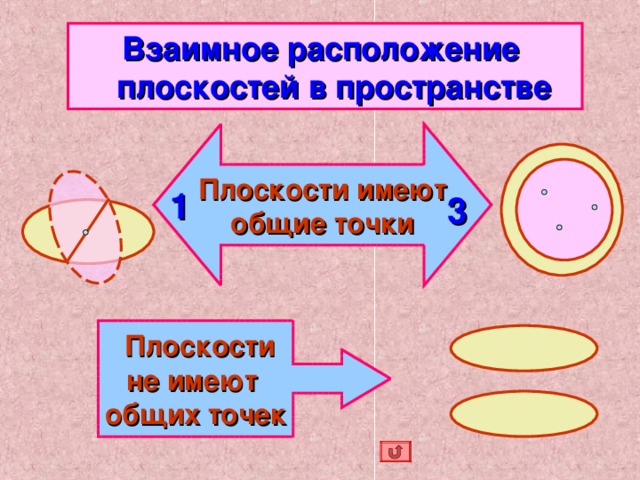
Возьмите плоскость ( листок бумаги ) и расположите её к другой плоскости ( столешнице парты ) так, чтобы у них не было общих точек; была одна общая точка; было три общих точки, не лежащие на одной прямой.
Каково взаимное расположение плоскостей в каждом случае?
С д е л а й т е в ы в о д
Дайте определение каждого из трёх случаев взаимного расположения двух плоскостей.
- плоскостипараллельны
- плоскостипересекаются
- плоскостисовпадают
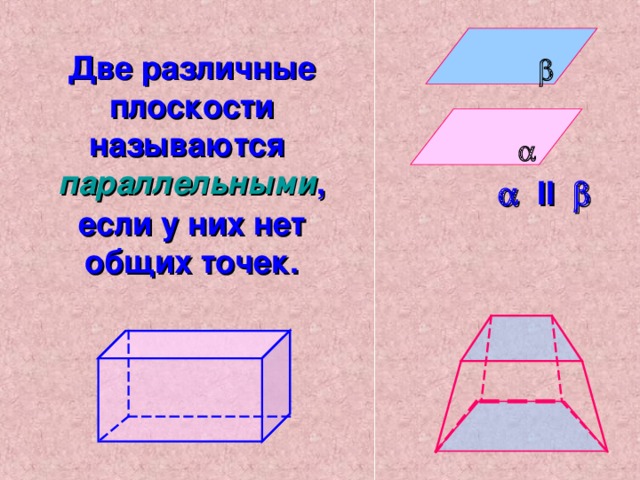
Две различные плоскости называются параллельными , если у них нет общих точек.

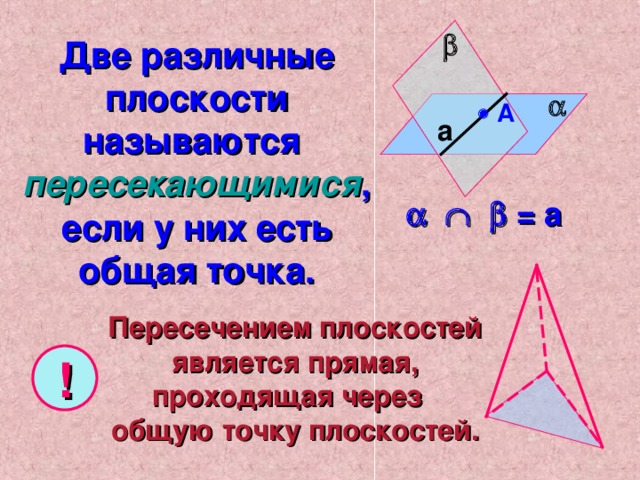
Две различные плоскости называются пересекающимися , если у них есть общая точка.
Пересечением плоскостей является прямая, проходящая через общую точку плоскостей.

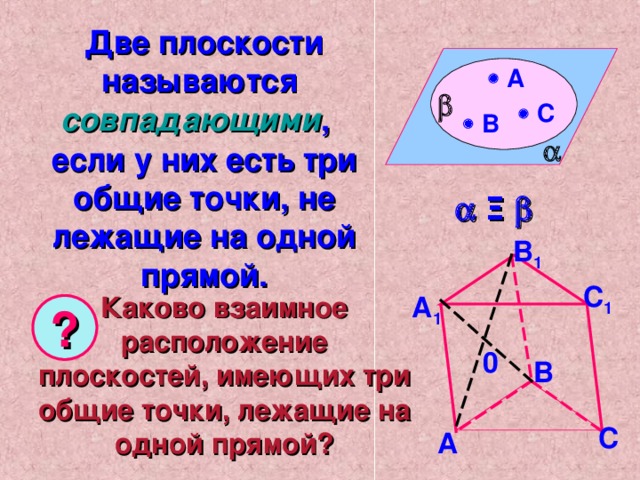
Две плоскости называются совпадающими , если у них есть три общие точки, не лежащие на одной прямой.
Каково взаимное расположение плоскостей, имеющих три общие точки, лежащие на одной прямой?
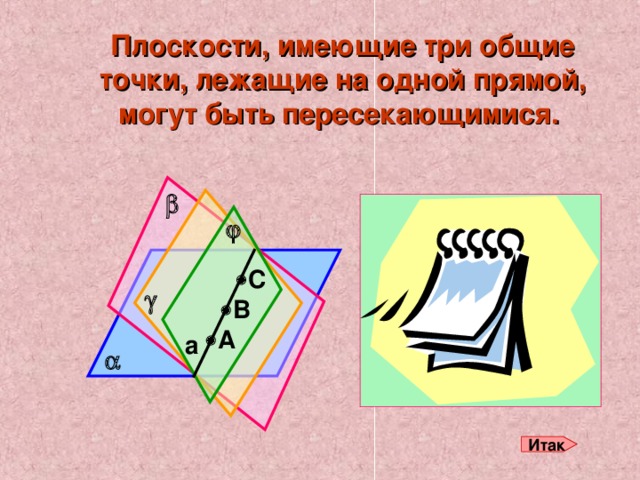
Плоскости, имеющие три общие точки, лежащие на одной прямой, могут быть пересекающимися.

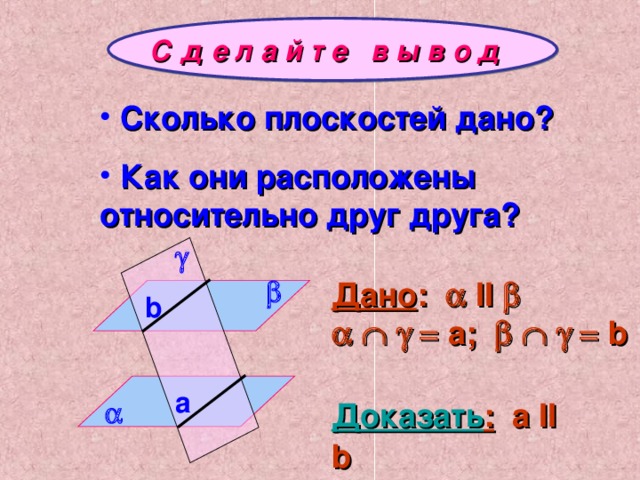
Т е о р е м а 1
Если две параллельные плоскости пересечены третьей плоскостью, то прямые пересечения параллельны.
Выделите условие и заключение теоремы.
С д е л а й т е в ы в о д
- Сколько плоскостей дано?
- Как они расположены относительно друг друга?
методом «от противного»
- какими могут быть между собой прямые «а» и «b»?
- если прямые «а» и «b» пересекаются, то какие между собой плоскости «» и «»?
- почему прямые «а» и «b» не могут быть скрещивающимися?
- какому условию противоречат итоги?Сделайте вывод о прямых «а» и «b».
Т е о р е м а 2
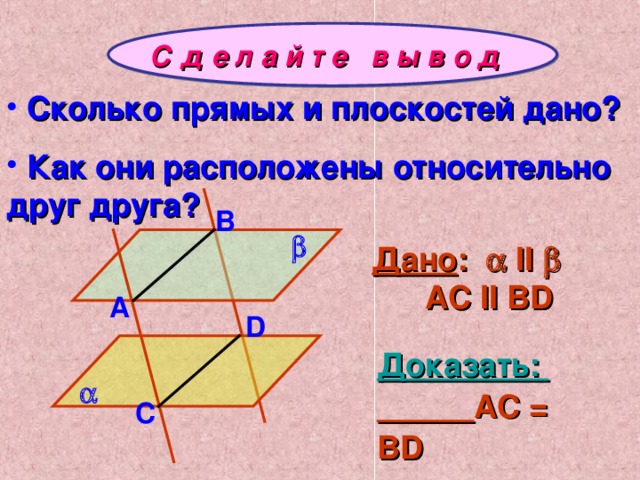
Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
Выделите условие и заключение теоремы.
С д е л а й т е в ы в о д
- Сколько прямых и плоскостей дано?
- Как они расположены относительно друг друга?
- рассмотрите четырёхугольник АВСD; что он из себя представляет?; почему?
- докажите, что АВСD—параллелограмм; на основании какой теоремы АВIIСD?
- воспользуйтесь свойствами сторон параллелограмма;
- сделайте вывод об отрезках АС и ВD
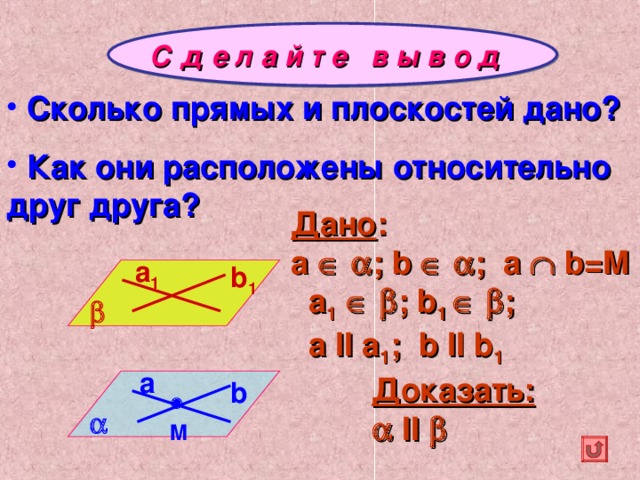
Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то данные плоскости параллельны.
Выделите условие и заключение теоремы.
С д е л а й т е в ы в о д
- Сколько прямых и плоскостей дано?
- Как они расположены относительно друг друга?
плоскостей в пространстве
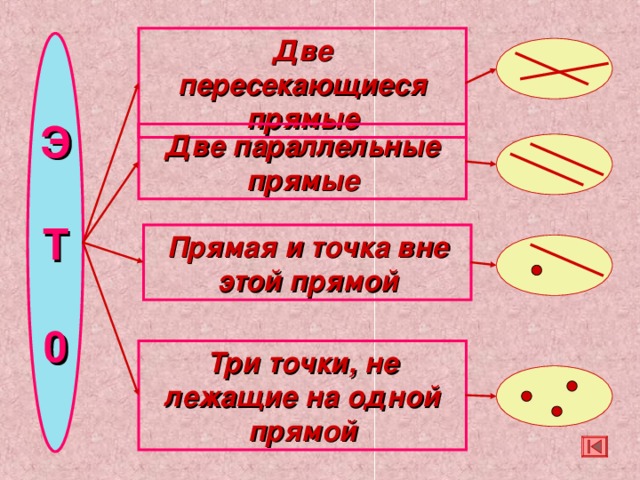
Выберите аксиому стереометрии , следствия из аксиом и определение , в которых говорится о существовании единственной плоскости.
Какой набор основных элементов ( точек и прямых ) необходимо иметь, чтобы задать единственную плоскость?
Две пересекающиеся прямые
Две параллельные прямые
Прямая и точка вне этой прямой
Три точки, не лежащие на одной прямой
Из истории начертательной геометрии
Ещё в древности человек чертил и рисовал на скалах, предметах быта изображения вещей, деревьев, животных и людей. Он делал это для удовлетворения своих потребностей. Основное требование – изображение должно было вызывать правильное зрительное представление о форме изображаемого предмета.
С ростом практических и технических применений изображений к ним стали предъявлять требования , чтобы по изображению можно было судить о геометрических свойствах, размерах. О таких требованиях можно судить по многим памятникам древности, уцелевшим до наших дней.
Строгие геометрически обоснованные правила изображения пространственных фигур (с соблюдением перспективы) стали систематически разрабатывать художники, архитекторы и скульпторы лишь в эпоху Возрождения: Леонардо да Винчи, Дюрер, Рафаэль, Микеланджело, Тициан и др.
Растущие запросы архитектуры, техники, промышленности, военного дела и живописи привели к формированию математической ветви – начертательной геометрии .
Французский математик Г. Монж разработал метод ортогонального проектирования пространственных фигур на две взаимно перпендикулярные плоскости, получая двойное изображение оригинала – на горизонтальной и вертикальной плоскостях.
Это даёт возможность решить и обратную задачу: восстановление пространственной фигуры или изучение её геометрических свойств по заданным плоским изображениям.
В школе наиболее употребительным является более наглядный аксонометрический метод (измерение по осям), основанный на параллельной проекции.
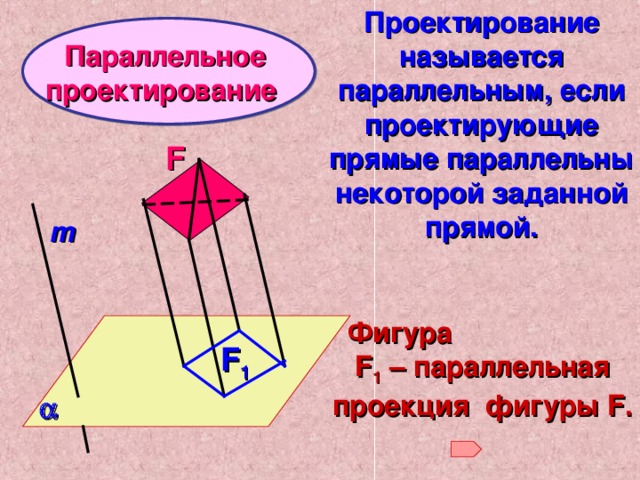
Проектирование называется параллельным, если проектирующие прямые параллельны некоторой заданной прямой.
Видео:10 класс, 5 урок, Параллельность трех прямыхСкачать

Параллельное проектирование. Изображение пространственных фигур 10 класс Атанасян
Презентация — лекция по теме урока.
Просмотр содержимого документа
«Параллельное проектирование. Изображение пространственных фигур 10 класс Атанасян»
«Параллельное проектирование. Изображение пространственных фигур»
Математика 10 класс
В стереометрии большое значение имеет умение наглядно изображать неплоские фигуры на плоскости. Вы знаете, что когда в планиметрии на листе бумаги изображают плоскую фигуру, то все точки изображённой фигуры лежат на плоскости листа. В стереометрии же рассматриваются фигуры, у которых не все точки расположены в одной плоскости. Поэтому надо знать правила, по которым изображают на плоскости пространственные фигуры. Итак, зачастую для изображения на плоскости (например, на листе бумаги) геометрических фигур, расположенных в пространстве, используется параллельное проектирование . Определяется оно следующим образом.
Пусть — некоторая плоскость, а — некоторая прямая, пересекающая эту плоскость. Возьмём в пространстве произвольную точку . Если точка не лежит на прямой , то проведём через точку прямую, параллельную прямой , и обозначим через точку пересечения этой прямой с плоскостью . Если же точка лежит на прямой , то обозначим через точку пересечения прямой с плоскостью .
- Точка называется проекциейточки на плоскость при проектировании параллельно прямой (или параллельной проекцией точки ).
- Плоскость называется плоскостью проекций , а о прямой говорят, что она задаёт направление проектирования .
- Все прямые, параллельные прямой , задают одно и то же направление проектирования, поэтому также называются проектирующими прямыми .
- Пусть — плоская или пространственная фигура. Проекцией фигуры на плоскость при проектировании параллельно прямой называется множество проекций всех точек фигуры .
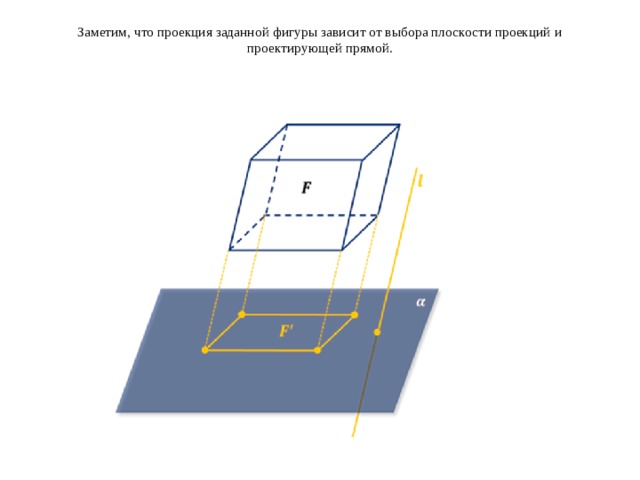
Заметим, что проекция заданной фигуры зависит от выбора плоскости проекций и проектирующей прямой.
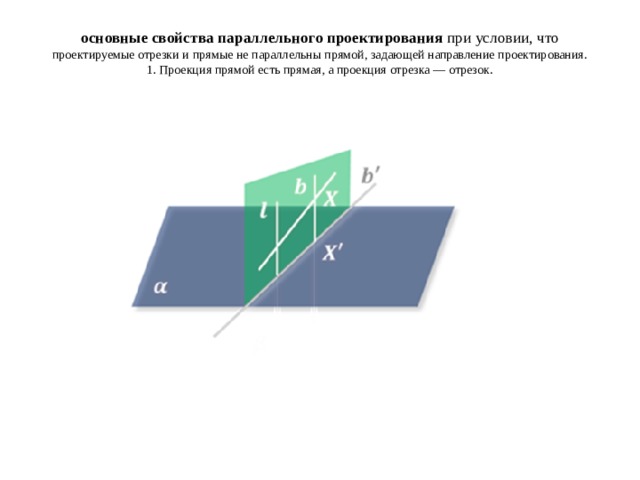
основные свойства параллельного проектирования при условии, что проектируемые отрезки и прямые не параллельны прямой, задающей направление проектирования. 1. Проекция прямой есть прямая, а проекция отрезка — отрезок.
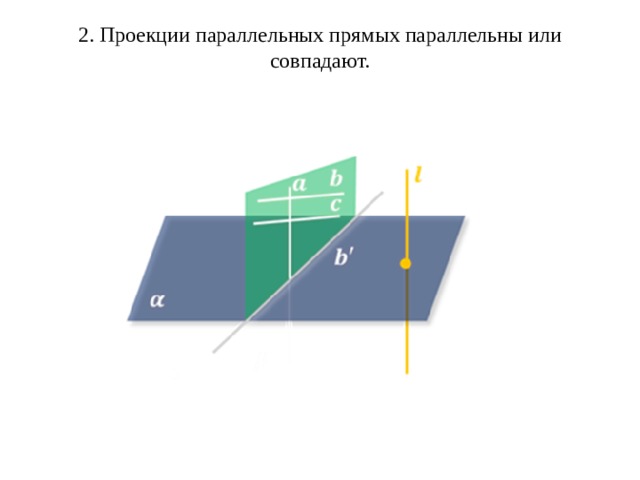
2. Проекции параллельных прямых параллельны или совпадают.
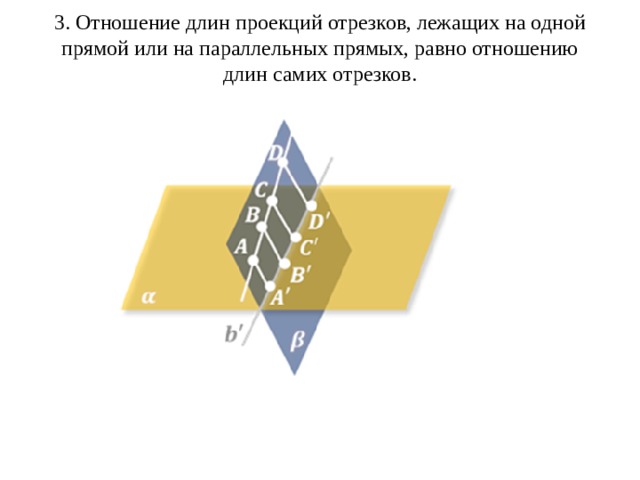
3. Отношение длин проекций отрезков, лежащих на одной прямой или на параллельных прямых, равно отношению длин самих отрезков.
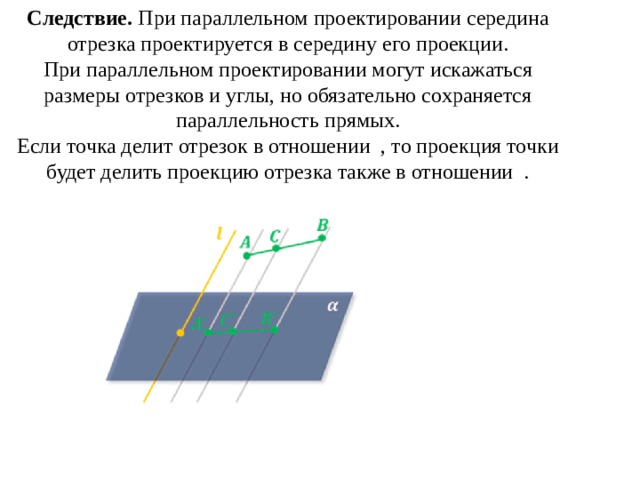
Следствие. При параллельном проектировании середина отрезка проектируется в середину его проекции. При параллельном проектировании могут искажаться размеры отрезков и углы, но обязательно сохраняется параллельность прямых. Если точка делит отрезок в отношении , то проекция точки будет делить проекцию отрезка также в отношении .
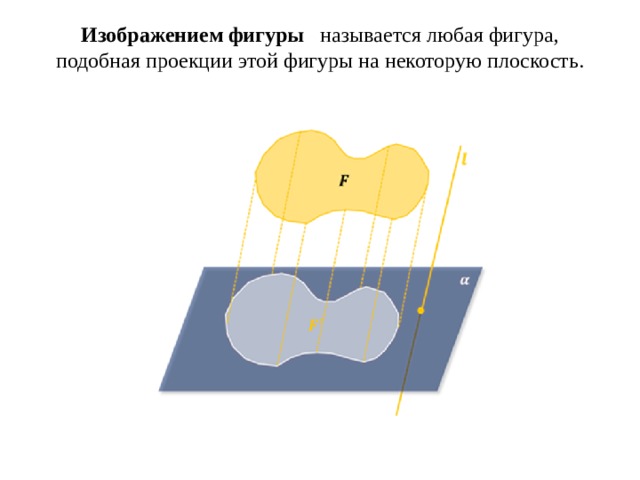
Изображением фигуры называется любая фигура, подобная проекции этой фигуры на некоторую плоскость.
- Выполняя изображения фигур, расположенных в пространстве, необходимо учитывать свойства, сохраняющиеся при параллельном проектировании, а в остальном изображение может быть произвольным. Важно только, чтобы изображения рассматриваемых фигур были наглядными и давали верное представление о них.
- При различном выборе плоскости проекций и направления проектирования получаются различные проекции данной фигуры, а значит, и различные её изображения.
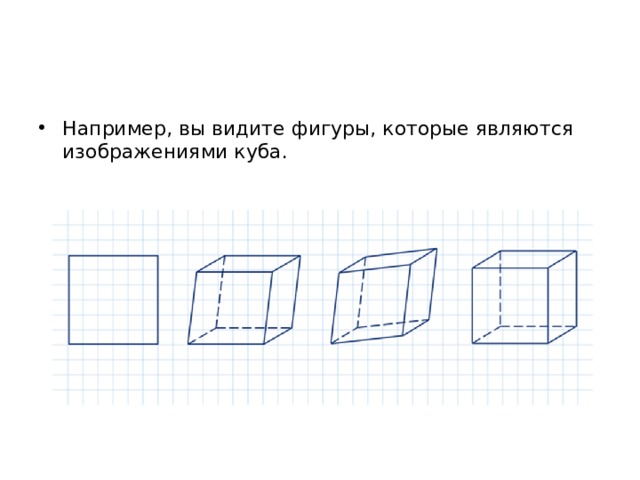
- Например, вы видите фигуры, которые являются изображениями куба.
Причём изображение куба, данное на первом рисунке, не даёт представления о кубе, наглядным является изображение, которое дано на последнем рисунке.
При построении изображений плоских фигур, расположенных в пространстве, предполагается, что плоскости рассматриваемых фигур не параллельны направлению проектирования.
Итак, проекцией треугольника может быть любой треугольник.
- Параллелограмм проектируется в параллелограмм, так как параллельные прямые сохраняют параллельность.
- В частном случае за изображение прямоугольника, квадрата, ромба можно принять любой параллелограмм.
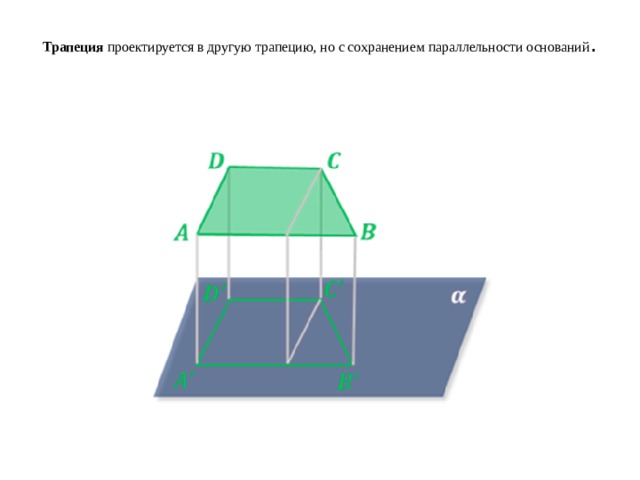
Трапеция проектируется в другую трапецию, но с сохранением параллельности оснований .
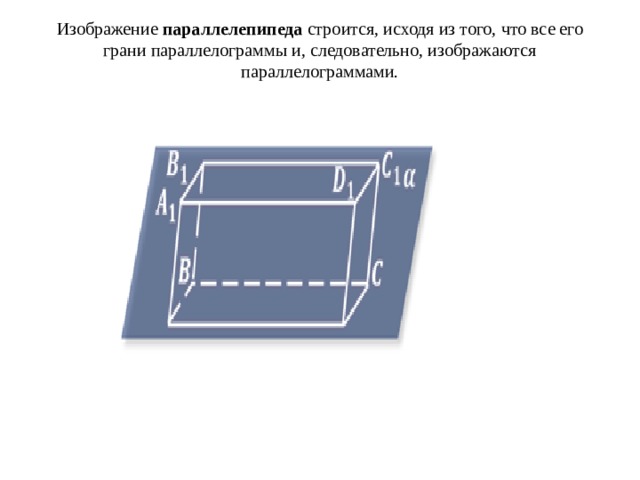
Изображение параллелепипеда строится, исходя из того, что все его грани параллелограммы и, следовательно, изображаются параллелограммами.
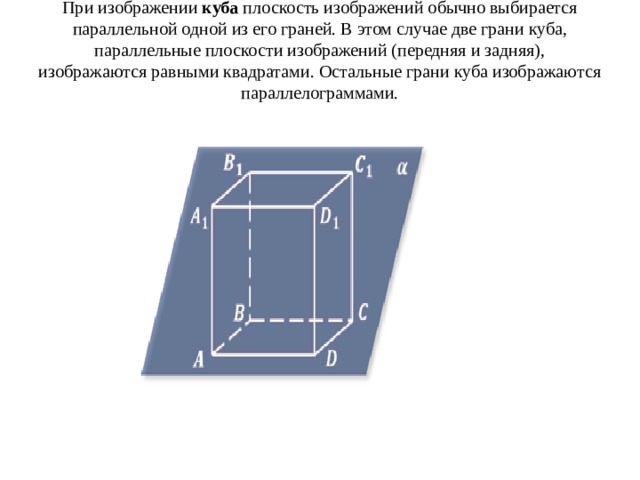
При изображении куба плоскость изображений обычно выбирается параллельной одной из его граней. В этом случае две грани куба, параллельные плоскости изображений (передняя и задняя), изображаются равными квадратами. Остальные грани куба изображаются параллелограммами.
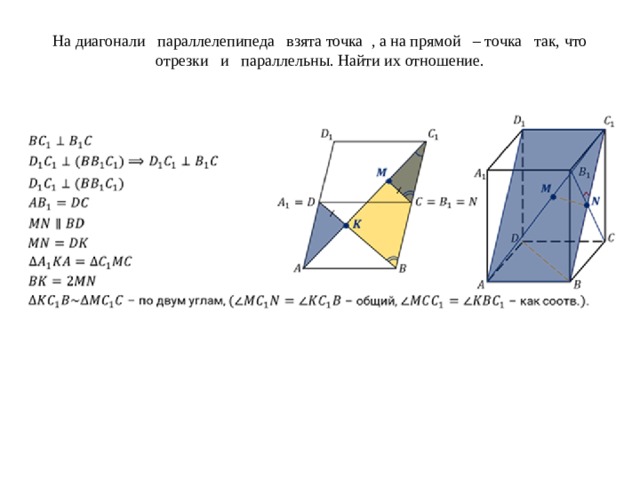
На диагонали параллелепипеда взята точка , а на прямой – точка так, что отрезки и параллельны. Найти их отношение.
📸 Видео
10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Следы прямой Взаимное положение двух прямыхСкачать

Взаимное расположение прямых в пространстве. 10 класс.Скачать

Параллельность прямых. 10 класс.Скачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

9 класс, 7 урок, Уравнение прямойСкачать

Параллельность прямых. Практическая часть. 10 класс.Скачать

19. Расстояние между параллельными прямыми Расстояние между скрещивающимися прямымиСкачать

Параллельность прямой и плоскости. 10 класс.Скачать

Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Уравнение параллельной прямойСкачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Параллельные прямые (задачи).Скачать

Параллельность прямой к плоскостиСкачать

Параллельные прямые циркулемСкачать

Построение недостающей проекции отрезка прямой линии, лежащей в заданной плоскостиСкачать

Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать