О чем эта статья:
- Прямоугольная декартова система координат
- Координаты точки в декартовой системе координат
- Где абсцисса а где ордината на графике
- Ось абсцисс, ось ординат
- содержание
- Этимология
- В параметрических уравнениях
- Смотрите также
- Рекомендации
- Синус это х или у в окружности
- Страницы
- среда, 7 ноября 2012 г.
- Тригонометрический круг синус и косинус
- Синус, косинус, тангенс и котангенс. Определения
- Угол поворота
- Числа
- Тригонометрические функции углового и числового аргумента
- Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
- Геометрическое определение синуса и косинуса
- Свойства синуса и косинуса
- Принятые обозначения
- Периодичность
- Четность
- Области определения и значений, экстремумы, возрастание, убывание
- Основные формулы, содержащие синус и косинус
- Сумма квадратов
- Формулы синуса и косинуса суммы и разности
- Формулы произведения синусов и косинусов
- Формулы суммы и разности
- Выражение синуса через косинус
- Выражение косинуса через синус
- Выражение через тангенс
- Таблица синусов и косинусов, тангенсов и котангенсов
- Выражения через комплексные переменные
- Формула Эйлера
- Выражения через гиперболические функции
- Производные
- Интегралы
- Разложения в ряды
- Секанс, косеканс
- Обратные функции
- Арксинус, arcsin
- Арккосинус, arccos
- Тригонометрическое определение
- Табличные значения синуса и косинуса
Видео:Координатная плоскость | Ось абсцисс | Ось ординат | МегаШкола | Математика 6 классСкачать

Прямоугольная декартова система координат
Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.
Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.
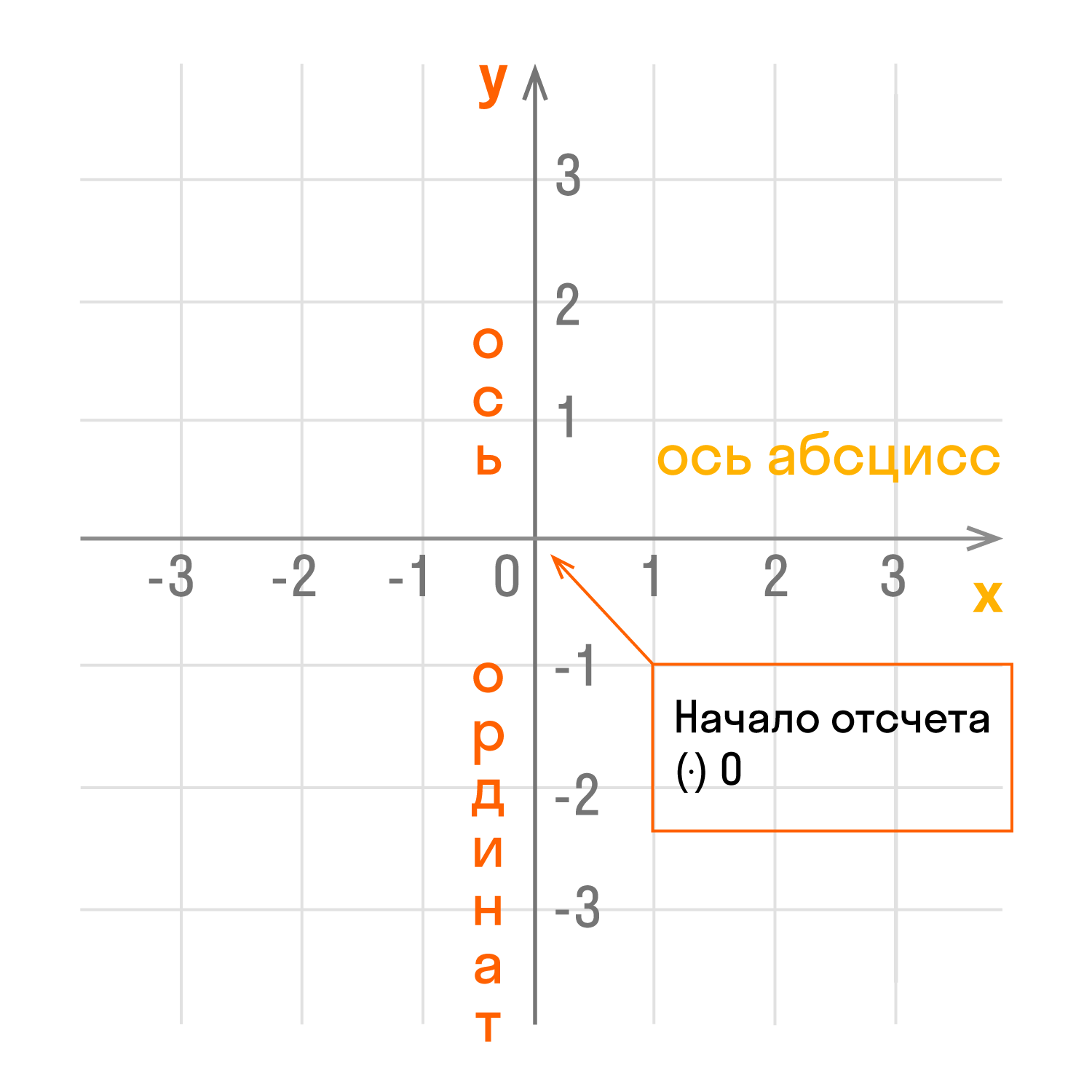
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.
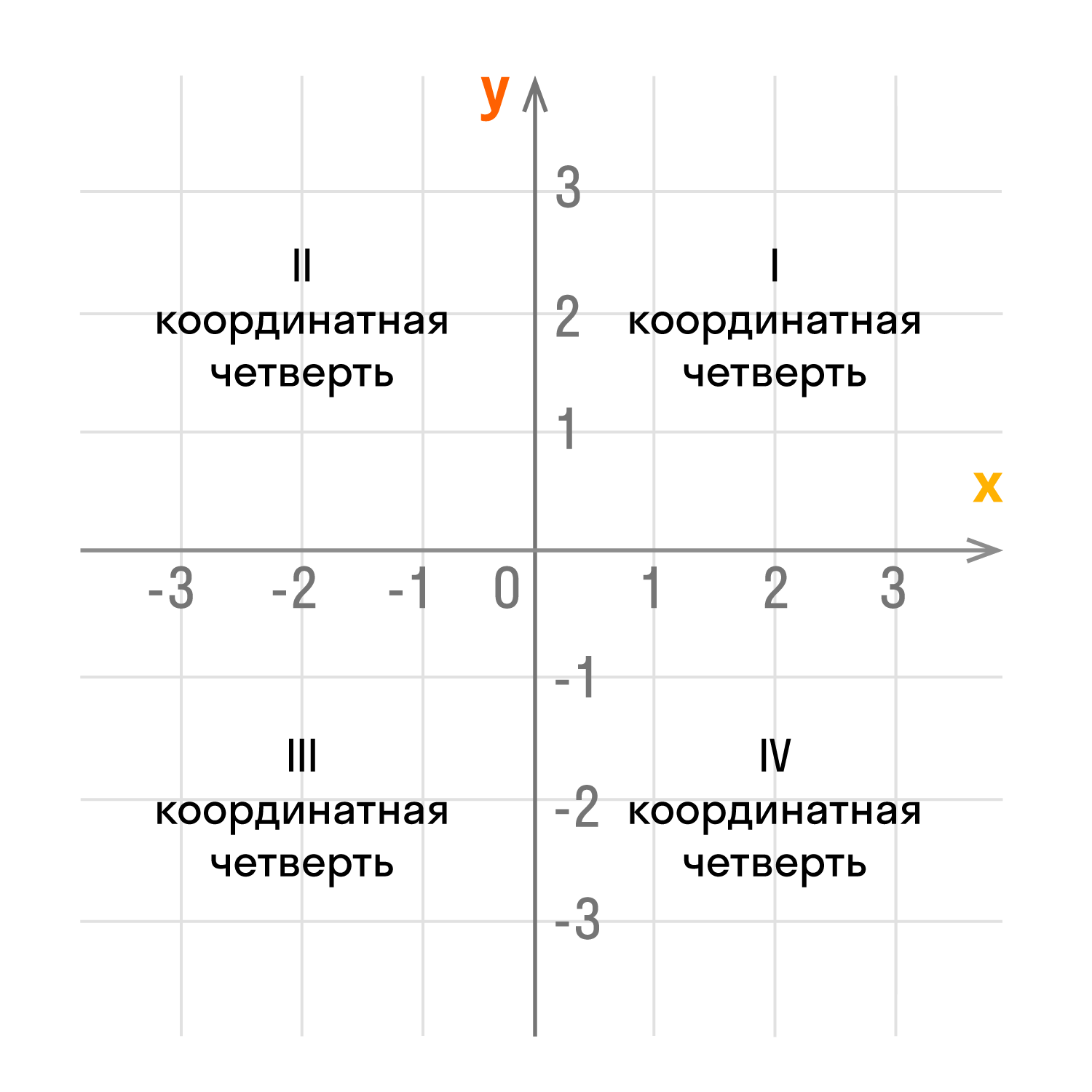
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Видео:10 класс, 11 урок, Числовая окружностьСкачать

Координаты точки в декартовой системе координат
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.
Каждая точка М, которая расположена на Ох, равна действительному числу xM. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.
Число xM — это координата точки М на заданной координатной прямой.
Пусть точка будет проекцией точки Mx на Ох, а My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения Mx и My.Тогда у точки Mx на оси Оx есть соответствующее число xM, а My на Оу — yM. Как это выглядит на координатных осях:
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (xM, yM), которые называются ее координатами. Абсцисса М — это xM, ордината М — это yM.
Обратное утверждение тоже верно: каждая пара (xM, yM) имеет соответствующую точку на плоскости.
Видео:Система координат · Ось абсцисс и ось ординат · Координатная плоскость Урок Математики для 6 классаСкачать

Где абсцисса а где ордината на графике
Знание — сила. Познавательная информация
Видео:№939. Найдите расстояние от точки М (3; -2): а) до оси абсцисс; б) до оси ординат;Скачать
Ось абсцисс, ось ординат
Эта ассоциация позволяет легко запомнить, что x — это ось абсцисс, а y — ось ординат и никогда больше не путать оси координат.
Ассоциация очень простая. Итак, есть ось абсцисс и ось ординат — ось x и ось y. Абсцисса начинается на букву «а», ордината — на букву «о». Что у нас в русском алфавите? Сначала идет буква «а», затем — буква «о». В латинском алфавите сначала идет «x», затем — «y». Соответственно, абсцисса — это x, ордината — это y.
Русский алфавит: а, о
Латинский алфавит: x, y
Соответствие: а-x, о-y ( А бсцисса — X , O рдината — Y ).
Для тех, кто путает, где на координатной плоскости ось x, а где — ось y, есть следующая ассоциация .
В прямоугольной системе координат ось X’X называется «осью абсцисс» .
При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Ординатой (от лат. ordinatus – расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат» .
При построении графиков функций, ось ординат обычно используется как область значений функции.
В прямоугольной системе координат ось X’X называется «осью абсцисс» .
При построении графиков функций, ось абсцисс обычно используется как область определения функции.
Ординатой (от лат. ordinatus – расположенный в порядке) точки A называется координата этой точки на оси Y’Y в прямоугольной системе координат. Величина ординаты точки A равна длине отрезка OC (см. рис. 1). Если точка C принадлежит положительной полуоси OY, то ордината имеет положительное значение. Если точка C принадлежит отрицательной полуоси Y’O, то ордината имеет отрицательное значение. Если точка A лежит на оси X’X, то её ордината равна нулю.
В прямоугольной системе координат ось Y’Y называется «осью ординат» .
При построении графиков функций, ось ординат обычно используется как область значений функции.
В математике , то по оси абсциссы ( / æ б ы ɪ с . Ə / ; множественная абсцисса или абсцисса или абсцисса ) и ординаты соответственно первые и вторые координаты из точки в системе координат .
Абсциссой точки является подписанный мерой его проекции на первичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный, после того, как : положительная).
Ордината точки является подписанный мерой его проекции на вторичной оси, чье абсолютное значение является расстоянием между проекцией и началом координат оси, и знак которого определяется местоположение на проекции относительно начала координат (до : отрицательный, после того, как : положительная).
Обычно это горизонтальные и вертикальные координаты точки в двумерной прямоугольной декартовой системе координат . Термины также могут относиться к горизонтальным и вертикальным осям , соответственно (обычно х -Axis и у -Axis) из двумерный графика. Упорядоченная пара состоит из двух слагаемых-оси абсцисс (горизонтальная, как правило , х ) и оси ординат (вертикальной, как правило , у ) -Какой определяют положение точки в двумерном пространстве прямоугольной.
( Икс ⏞ абсцисса , Y ⏞ ордината ) ^ >, overbrace ^ >)>
Видео:10 класс, 12 урок, Числовая окружность на координатной плоскостиСкачать

содержание
Видео:АбсциссаСкачать

Этимология
Хотя слово «абсцисса» (лат; «Linea абсцисса», «линия отрезана») используется , по крайней мере , так как De Practica Geometrie , опубликованной в 1220 году Фибоначчи (Леонардо из Пизы), его использование в его современном понимании может быть связано венецианский математик Стефано дельи Анджели в своей работе Miscellaneum Hyperbolicum, и др Parabolicum 1659.
В 1892 работы Лекциях по теории über Geschichte дер Mathematik, Том 2, ( « Лекции по истории математики ») немецкий историк математики Мориц Кантор пишет
«Wir Кеннен Keine ältere Benutzung де Wortes Abssisse в lateinischen Originalschriften [чем дельи Анджели – х]. Vielleicht Kommt дас Сусло в Übersetzungen дер Apollonischen Kegelschnitte VOR, WO Buch I Satz 20 из ἀποτεμνομέναις фильеры Rede ист, wofür ES Kaum Ein entsprechenderes lateinisches Сусло ALS абсцисса Гебен möchte «. «Мы не знаем , не ранее использования слова абсциссы латинских оригиналов [чем дельи Анджели – х]. Может быть , это слово происходит от переводов Аполлона коника , где в книге I, Глава 20 там появляется ἀποτεμνομέναις, для которых вряд ли было бы в случае необходимости латинское слово , как по оси абсцисс. «
Видео:№1011. Ответьте на вопросы: а) Может ли абсцисса точки единичной полуокружности иметь значения 0,3Скачать
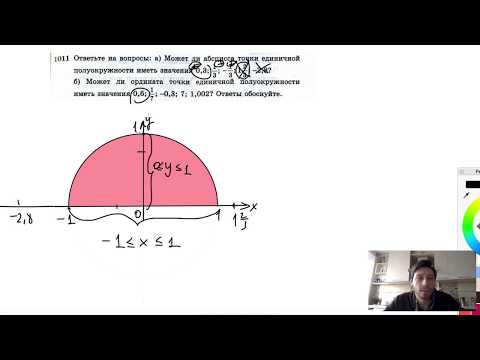
В параметрических уравнениях
В нескольких устаревшей использовании варианты, абсцисса точки может также относиться к любому числу , которое описывает положение точки вдоль некоторого пути, например параметр в параметрическом уравнении . Используемый в этом случае, по оси абсцисс можно рассматривать как координатно-геометрию аналога к независимой переменной в математической модели или эксперимента (с любыми ординат , заполняющих роль , аналогичную зависимых переменных ).
Видео:Алгебра 7 класс. 28 сентября. Зная абсциссу найти ординатуСкачать

Смотрите также
Видео:Алгебра 10 класс. 20 сентября. Числовая окружность #6 координаты точекСкачать

Рекомендации
Эта статья основана на материале , взятом из Бесплатный он-лайн словарь вычислительной до 1 ноября 2008 года и зарегистрированная в соответствии с «релицензировании» с точки зрения GFDL , версии 1.3 или более поздней версии.
Видео:Точки пересечения графика линейной функции с координатными осями. 7 класс.Скачать

Синус это х или у в окружности
Математика – это очень просто, даже проще, чем мы можем себе представить. Сложной математику делают сами математики.
Видео:Абсцисса / Ордината🥲 #математика #егэ #умскулСкачать

Страницы
Видео:Уравнение окружности с центром на оси абсцисс, ординат или в начале координат. Урок 3. Геометрия 8.Скачать

среда, 7 ноября 2012 г.
Тригонометрический круг синус и косинус
Тригонометрический круг представляет значения тригонометрических функций синус (sin) и косинус (cos) в виде координат точек единичной окружности при различных значениях угла альфа в градусах и радианах.
Поскольку я сам вечно путаюсь при переводе координат точек окружности в синусы и косинусы, для простоты все значения косинусов (cos) для углов от 0 до 360 градусов (от 0 пи до 2 пи) подчеркнуты зеленой черточкой. Даже при распечатке этого рисунка тригонометрического круга на черно-белом принтере все значения косинуса будут подчеркнуты, а значения синуса будут без подчеркивания. Если вам интересно, то можете посмотреть отдельные тригонометрические круги для синуса и косинуса.
Напротив указанных углов на окружности расположены точки, а в круглых скобках указаны координаты этих точек. Первой записана координата Х (косинус)
Давайте проведем обзорную экскурсию по этому уголку математического зоопарка. Прежде всего, нужно отметить, что здесь присутствует декартова система координат – одна черная горизонтальная линия с буковкой Х возле стрелочки, вторая – вертикальная линия с буковкой У. На оси Х, которую еще называют ось абсцисс (это умное слово математики придумали специально, что бы запутать блондинок) живут косинусы – cos. На оси У, которую называют ось ординат (еще одно умное слово, которое в устах блондинки может стать убийственным оружием), живут синусы – sin. Если посмотреть на семейную жизнь этих тригонометрических функций, то не трудно заметить, что синусы всегда на кухне у плиты по вертикали, а косинусы – на диване перед телевизором по горизонтали.
В этой системе координат нарисована окружность радиусом, равным единице. Центр окружности находится в начале системы координат – там, где в центе рисунка пересекаются оси абсцисс (ось Х) и ординат (ось У).
Из центра окружности проведены тоненькие черточки, которые показывают углы 30, 45, 60, 120, 135, 150, 210, 225, 240, 300, 315, 330 градусов. В радианной мере углов это пи деленное на 6, пи на 4, пи на 3, 2 пи на 3, 3 пи на 4, 5 пи на 6, 7 пи на 6, 5 пи на 4, 4 пи на 3, 3 пи на 2, 5 пи на 3, 7 пи на 4, 11 пи деленное на 6. С осями координат совпадают такие значения углов: 0, 90, 180, 270 градусов или 0 пи, пи деленное на 2, пи, 3 пи деленное на 2. Пользуясь картинкой, очень просто переводить углы из градусов в радианы и из радиан в градусы. Одинаковые значения в разных системах измерения углов написаны на одной линии, изображающей этот угол.
Линии углов заканчиваются точками на единичной окружности. Возле каждой точки, в круглых скобках, записаны координаты этой точки. Первой записана координата Х, которая соответствует косинусу угла, образовавшего эту точку. Второй записана координата У этой точки, что соответствует значению синуса угла. По картинке довольно легко находить синус и косинус заданного угла и наоборот, по заданному значению синуса или косинуса, можно легко найти значение угла. Главное, не перепутать синус с косинусом.
Обращаю особое внимание на тот факт, что если вы по значению синуса или косинуса ищите угол, обязательно нужно дописывать период угла. Математики очень трепетно относятся к этому аппендициту тригонометрических функций и при его отсутствии могут влепить двойку за, казалось бы, правильный ответ. Что такое период при нахождении угла по значению тригонометрической функции? Это такая штучка, которая придумана математиками специально для того, чтобы запутываться самим и запутывать других. Особенно блондинок. Но об этом мы поговорим как-нибудь в другой раз.
Всё, что собрано в кучку на рисунке тригонометрического круга синуса и косинуса, можно внимательно рассмотреть на отдельных картинках с портретами синуса 0, 30, 45 градусов (ссылки на отдельные странички я буду добавлять по мере увеличения фотогалереи синусов и косинусов).
Синусы и косинусы круг – здесь картинка во всей своей тригонометрической красе.
Угол 120 градусов в радианах – равен 2/3 пи или 2 пи деленное на 3, на картинке очень красиво нарисовано.
Значения синусов косинусов углов в радианах – на картинке есть такие, надеюсь, именно те углы, которые вы ищете.
Значение косинуса угла в 45 градусов – равно корню из двух деленному на два, можете проверить по рисунку.
Тригонометрическая окружность – я не совсем уверен, что представленная на картинке окружность является тригонометрической, но что-то от тригонометрии в этой окружности определенно есть, например, синусы и косинусы на окружности – вылитая тригонометрия.
Тригонометрический круг рисунок – есть здесь такой. Правда, не самый красивый рисунок, можно нарисовать гораздо красивее и понятнее. Мне минус в репутацию – почему я до сих пор не нарисовал его для блондинок? Представляете ситуацию в картинной галерее будущего: экскурсовод объясняет группе школьников «Перед вами всемирно известное полотно «Тригонометрическая мадонна с единичным отрезком на руках» – картина гениального художника эпохи Раннего Математического Возрождения . » Дальше она называет имя этого самого художника (или художницы). Это имя может быть вашим!
Круг синусов и косинусов – именно такой круг совершенно случайно оказался здесь на картинке.
Угол 9 градусов сколько это в пи – в пи это 1/20 или пи/20.
Решение: для перевода градусов в пи радиан, нужно имеющиеся у нас градусы разделить на 180 градусов (это 1 пи радиан). У нас получается 9/180 = 1/20
Ответ: 9 градусов = 1/20 пи.
Синус это вверх или в сторону – синус – это вверх, в сторону – это косинус.
Комментарии к этой статье запрещены. Из-за огромного их количества мои ответы на ваши вопросы о тригонометрическом круге уже не публикуются. Вопросы можете задавать в комментариях к другим страницам. Постараюсь решить проблему за счет удаления части комментариев, тем самым освобожу место для новых.
Тригонометрия – раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Видео:135 Сумма векторов. Абсцисса, ордината, аппликата. (240)Скачать

Синус, косинус, тангенс и котангенс. Определения
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла ( sin α ) – отношение противолежащего этому углу катета к гипотенузе.
Косинус угла ( cos α ) – отношение прилежащего катета к гипотенузе.
Тангенс угла ( t g α ) – отношение противолежащего катета к прилежащему.
Котангенс угла ( c t g α ) – отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса – вся числовая прямая, то есть эти функции могут принимать любые значения.
Видео:Точки на числовой окружностиСкачать

Угол поворота
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от – ∞ до + ∞ .
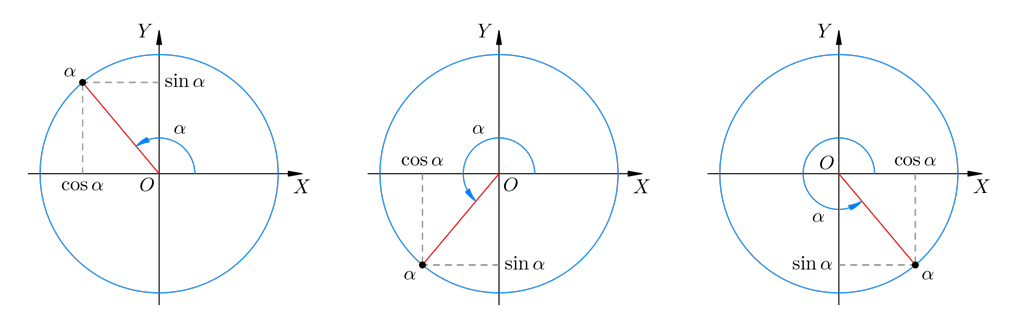
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами ( 1 , 0 ) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 . Определение дается через координаты точки A 1 ( x , y ).
Синус (sin) угла поворота
Синус угла поворота α – это ордината точки A 1 ( x , y ). sin α = y
Косинус угла поворота α – это абсцисса точки A 1 ( x , y ). cos α = х
Тангенс угла поворота α – это отношение ординаты точки A 1 ( x , y ) к ее абсциссе. t g α = y x
Котангенс угла поворота α – это отношение абсциссы точки A 1 ( x , y ) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой ( 0 , 1 ) и ( 0 , – 1 ). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z )
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z )
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Видео:9 класс. Геометрия. Тригонометрические функции угла от 0° до 180°. Единичная окружность. Урок #1Скачать

Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности – точка A c координатами ( 1 , 0 ).
Положительному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t – ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус числа t – абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс числа t – отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t, совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Видео:Косинус абсцисса синус ордината от Анны МалковойСкачать

Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).
Можно сказать, что sin α , cos α , t g α , c t g α – это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс – основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Видео:Алгебра 10 класс (Урок№30 - Определение синуса, косинуса и тангенса угла.)Скачать

Связь определений sin, cos, tg и ctg из геометрии и тригонометрии
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A ( 1 , 0 ) на угол величиной до 90 градусов и проведем из полученной точки A 1 ( x , y ) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 ( x , y ) . Длина катета, противолежащего углу, равна ординате точки A 1 ( x , y ) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Видео:Прямоугольная система координат. Координатная плоскость. 6 класс.Скачать

Геометрическое определение синуса и косинуса
α – угол, выраженный в радианах.
Видео:Выступление команд Абсцисса и ОрдинатаСкачать

Свойства синуса и косинуса
Видео:Как найти координаты точек на тригонометрической окружностиСкачать

Принятые обозначения
( sin^2 x equiv (sin x)^2; ) ( quad sin^3 x equiv (sin x)^3; ) ( quad sin^n x equiv (sin x)^n ) ( sin^ x equiv arcsin x ) ( (sin x )^ equiv dfrac1 equiv cosec x ) .
( cos^2 x equiv (cos x)^2; ) ( quad cos^3 x equiv (cos x)^3; ) ( quad cos^n x equiv (cos x)^n ) ( cos^ x equiv arccos x ) ( (cos x )^ equiv dfrac1 equiv sec x ) .
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
( sin(x + 2pi) = sin x; quad ) ( cos(x + 2pi) = cos x )
Четность
Функция синус – нечетная. Функция косинус – четная.
( sin( -x ) = – sin x; quad ) ( cos( -x ) = cos x )
Области определения и значений, экстремумы, возрастание, убывание
Основные свойства синуса и косинуса представлены в таблице (n – целое).
| ( small -dfrac 2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) | ( small -pi + 2pi n ) ( small ( small 2pi n ) | |
| Убывание | ( small dfrac 2 + 2pi n ) ( small ( small dfrac 2 + 2pi n ) | ( small 2pi n ) ( small ( pi + small 2pi n ) |
| Максимумы, ( small x = ) ( small dfrac 2 + 2pi n ) | ( small x = 2pi n ) | |
| Минимумы, ( small x = ) ( small -dfrac 2 + 2pi n ) | ( small x = ) ( small pi + 2pi n ) | |
| Нули, ( small x = pi n ) | ( small x = dfrac 2 + pi n ) | |
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы, содержащие синус и косинус
Сумма квадратов
( sin^2 x + cos^2 x = 1 )
Формулы синуса и косинуса суммы и разности
( sin(x + y) = sin x cos y + cos x sin y )
( sin(x – y) = sin x cos y – cos x sin y )
( cos(x + y) = cos x cos y – sin x sin y )
( cos(x – y) = cos x cos y + sin x sin y )
( sin( 2x ) = 2 sin x cos x )
( cos( 2x ) = cos^2 x – sin^2 x = ) ( 2 cos^2 x – 1 = 1 – 2 sin^2 x )
( cosleft( dfrac
2 – x
ight) = sin x ) ; ( sinleft( dfrac
2 – x
ight) = cos x )
( cos( x + pi ) = – cos x ) ; ( sin( x + pi ) = – sin x )
Формулы произведения синусов и косинусов
( sin x cos y = ) ( dfrac12 sin( x – y ) + sin( x + y ) )
( sin x sin y = ) ( dfrac12 cos( x – y ) – cos( x + y ) )
( cos x cos y = ) ( dfrac12 cos( x – y ) + cos( x + y ) )
( sin x cos y = dfrac12 sin 2x )
( sin^2 x = dfrac12 1 – cos 2x )
( cos^2 x = dfrac12 1 + cos 2x )
Формулы суммы и разности
( sin x + sin y = 2 , sin dfrac2 , cos dfrac2 )
( sin x – sin y = 2 , sin dfrac2 , cos dfrac2 )
( cos x + cos y = 2 , cos dfrac2 , cos dfrac2 )
( cos x – cos y = 2 , sin dfrac2 , sin dfrac2 )
Выражение синуса через косинус
Далее мы полагаем, что ( n ) – целое число.
Выражение косинуса через синус
Выражение через тангенс
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
[ img style=»max-w ]
Выражения через комплексные переменные
Формула Эйлера
( e^ = cos z + i sin z )
Выражения через гиперболические функции
( sin iz = i sh z ) ( cos iz = ch z )
( sh iz = i sin z ) ( ch iz = cos z )
Производные
( ( sin x )’ = cos x ) ( ( cos x )’ = – sin x ) . Вывод формул > > >
Производные n-го порядка:
( left( sin x
ight)^ = sinleft( x + ndfrac
2
ight) ) ( left( cos x
ight)^ = cosleft( x + ndfrac
Интегралы
( int sin x , dx = – cos x + C ) ( int cos x , dx = sin x + C )
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
Секанс, косеканс
( sec x = dfrac1 ; ) ( cosec x = dfrac1 )
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
( y = arcsin x ) ( left )
( sin( arcsin x ) = x ) ( )
( arcsin( sin x ) = x ) ( left )
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрическое определение
С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.
На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.
Рис. 2. Тригонометрическое определение синуса и косинуса
Косинус угла – это абсцисса точки. Синус угла – это ордината точки.
На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.
Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.
Рис. 3. Синус и косинус во II, III и IV четвертях
Табличные значения синуса и косинуса
Абсцисса точки 0 равна 1 , ордината точки 0 равна 0 . Следовательно,