Cos x положителен в следующих четвертях единичной окружности

Вопросы, возникающие при изучении тригонометрических функций, разнообразны. Некоторые из них – о том, в каких четвертях косинус положительный и отрицательный, в каких четвертях синус положительный и отрицательный. Все оказывается просто, если знаешь, как вычислить значение данных функций в разных углах и знаком с принципом построения функций на графике.

Видео:Знаки синуса, косинуса, тангенса ЛекцияСкачать

Какие значения косинуса

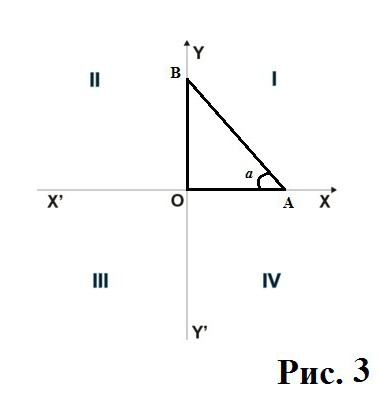
Если рассматривать прямоугольный треугольник, то мы имеем следующее соотношение сторон, которое его определяет: косинусом угла а является отношение прилегающего катета ВС к гипотенузе АВ (рис. 1): cos a = ВС/АВ.

С помощью этого же треугольника можно найти синус угла, тангенс и котангенс. Синусом будет соотношение противоположного к углу катета АС к гипотенузе АВ. Тангенс угла находится, если синус искомого угла разделить на косинус того же угла; подставив соответственные формулы нахождения синуса и косинуса, получим, что tg a = АС/ВС. Котангенс, как обратная к тангенсу функция, будет находиться так: ctg a = ВС/АС.

То есть, при одинаковых значениях угла обнаружилось, что в прямоугольном треугольнике соотношение сторон всегда одинаковое. Казалось бы, стало ясно, откуда эти значения, но почему получаются отрицательные числа?

Для этого нужно рассматривать треугольник в декартовой системе координат, где присутствуют как положительные, так и отрицательные значения.

Видео:Преобразование выражения A sin x + В cos x к виду С sin (х + t) | Алгебра 10 класс #38 | ИнфоурокСкачать

Наглядно про четверти, где какая

Видео:Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Первая четверть

Если разместить прямоугольный треугольник в первой четверти (от 0 о до 90 о ), где ось х и у имеют положительные значения (отрезки АО и ВО лежат на осях там, где значения имеют знак «+»), то что синус, что косинус тоже будут иметь положительные значения, и им присвоено значение со знаком «плюс». Но что происходит, если переместить треугольник во вторую четверть (от 90 о до 180 о )?

Видео:Найти знак тригонометрической функции (bezbotvy)Скачать

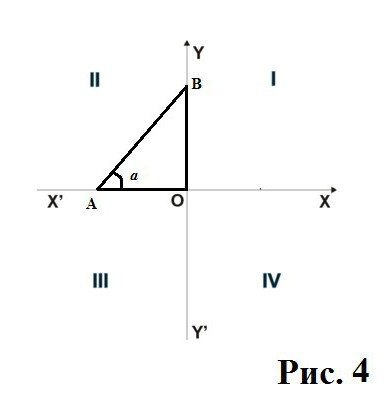
Вторая четверть

Видим, что по оси у катет АО получил отрицательное значение. Косинус угла a теперь имеет в соотношении эту сторону с минусом, потому и итоговое его значение становится отрицательным. Выходит, что то, в какой четверти косинус положительный, зависит от размещения треугольника в системе декартовых координат. И в этом случае косинус угла получает отрицательное значение. А вот для синуса ничего не изменилось, ведь для определения его знака нужна сторона ОВ, которая осталась в данном случае со знаком плюс. Подведем итог по первым двум четвертям.

Чтобы выяснить, в каких четвертях косинус положительный, а в каких отрицательный (а также синус и другие тригонометрические функции), необходимо смотреть на то, какой знак присвоен тому или иному катету. Для косинуса угла a важен катет АО, для синуса – ОВ.

Первая четверть пока что стала единственной, отвечающей на вопрос: «В каких четвертях синус и косинус положительный одновременно?». Посмотрим далее, будут ли еще совпадения по знаку этих двух функций.

Во второй четверти катет АО стал иметь отрицательное значение, а значит и косинус стал отрицательным. Для синуса сохранено положительное значение.

Видео:Знаки тригонометрических функций. 9 класс.Скачать

Третья четверть

Теперь оба катета АО и ОВ стали отрицательными. Вспомним соотношения для косинуса и синуса:

АВ всегда имеет положительный знак в данной системе координат, так как не направлена ни в одну из двух определённых осями сторон. А вот катеты стали отрицательными, а значит и результат для обоих функций тоже отрицательный, ведь если производить операции умножения или деления с числами, среди которых одно и только одно имеет знак «минус», то результат тоже будет с этим знаком.

Итог на данном этапе:

1) В какой четверти косинус положительный? В первой из трех.

2) В какой четверти синус положительный? В первой и второй из трёх.

Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

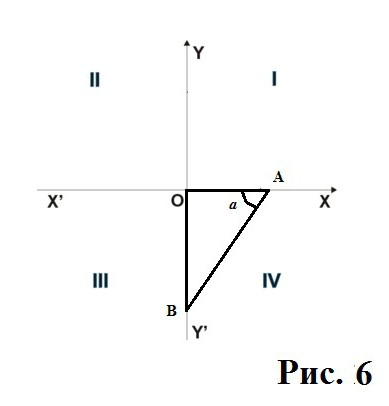
Четвёртая четверть (от 270 о до 360 о )

Здесь катет АО вновь приобретает знак «плюс», а значит и косинус тоже.

Для синуса дела всё еще «отрицательны», ведь катет ОВ остался ниже начальной точки О.

Видео:Тригонометрическая функция, y=cosx и ее свойства. 10 класс.Скачать

Выводы

Для того чтобы понимать, в каких четвертях косинус положительный, отрицательный и т.д., нужно запомнить соотношение для вычисления косинуса: прилегающий к углу катет, деленный на гипотенузу. Некоторые учителя предлагают запомнить так: к(осинус) = (к) углу. Если запомнить этот «чит», то автоматически понимаешь, что синус – это отношение противоположного к углу катета к гипотенузе.

Запомнить, в каких четвертях косинус положительный, а в каких отрицательный, довольно сложно. Тригонометрических функций много, и все они имеют свои значения. Но все же, как итог: положительные значения для синуса – 1, 2 четверти (от 0 о до 180 о ); для косинуса 1, 4 четверти (от 0 о до 90 о и от 270 о до 360 о ). В остальных четвертях функции имеют значения с минусом.

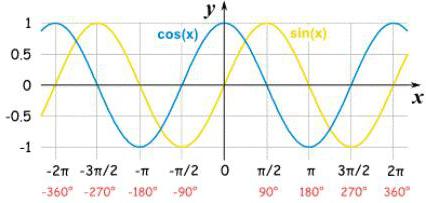
Возможно, кому-то будет легче запомнить, где какой знак, по изображению функции.

Для синуса видно, что от нуля до 180 о гребень находится над линией значений sin(x), значит и функция здесь положительна. Для косинуса так же: в какой четверти косинус положительный (фото 7), а в какой отрицательный видно по перемещению линии над и под осью cos(x). Как итог, мы можем запомнить два способа определения знака функций синус, косинус:

1. По мнимому кругу с радиусом равным единице (хотя, на самом деле, не важно, какой радиус у круга, но в учебниках чаще всего приводят именно такой пример; это облегчает восприятие, но в то же время, если не оговориться, что это не суть важно, дети могут запутаться).

2. По изображению зависимости функции по (х) от самого аргумента х, как на последнем рисунке.

С помощью первого способа можно ПОНЯТЬ, от чего именно зависит знак, и мы подробно разъяснили это выше. Рисунок 7, построенный по этим данным, как нельзя лучше визуализирует полученную функцию и ее знакопринадлежность.

Видео:Алгебра 10 класс (Урок№41 - Уравнение cos x = a.)Скачать

Косинус

Коcинус – одна из тригонометрических функций. Значение косинуса определяется для угла или для числа (в этом случае используют числовую окружность).

Видео:Как решать тригонометрические неравенства?Скачать

Аргумент и значение

Видео:Синус, косинус произвольного угла. 9 класс.Скачать

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)

Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.

Видео:Отбор корней по окружностиСкачать

Косинус числа

Косинус числа можно определить с помощью числовой окружности – косинус числа равен абсциссе соответствующей точки на ней.

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи : (frac) , (frac) , (-2π).

Например, для числа (frac) — косинус будет равен (frac<sqrt>) . А для числа (-) (frac) он будет равен (-) (frac<sqrt>) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице .

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Видео:Тригонометрические функции и их знакиСкачать

Косинус любого угла

Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.

Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.

Видео:Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

Знаки косинуса по четвертям

С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:

— там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos⁡1) – положителен.
Ответ: плюс.

Видео:ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, КотангенсСкачать

Связь с другими тригонометрическими функциями:

— синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
— тангенсом того же угла (или числа): формулой (1+tg^2⁡x=) (frac)
— котангенсом и синусом того же угла (или числа): формулой (ctgx=) (frac<cos>)
Другие наиболее часто применяемые формулы смотри здесь .

Видео:Вычисление значений тригонометрических функцийСкачать

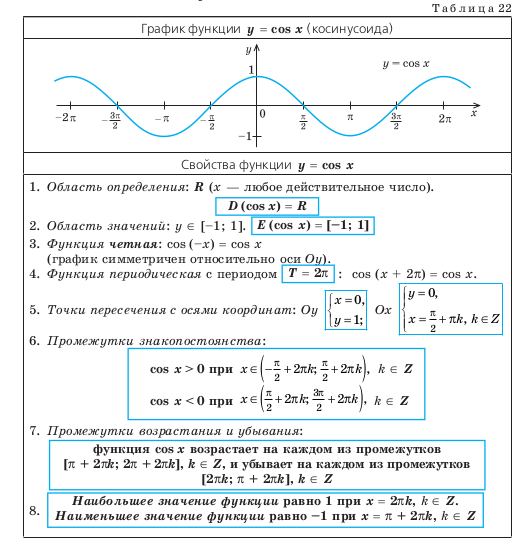
Функция (y=cos)

Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:

— область определения – любое значение икса: (D(cos )=R)
— область значений – от (-1) до (1) включительно: (E(cos )=[-1;1])
— четная: (cos⁡(-x)=cos)
— периодическая с периодом (2π): (cos⁡(x+2π)=cos)
— точки пересечения с осями координат:
ось абсцисс: (() (frac) (+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
— промежутки знакопостоянства:
функция положительна на интервалах: ((-) (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (() (frac) (+2πn;) (frac) (+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).

Видео:Построение графика функции y = cos xСкачать

14. Свойства функций синуса, косинуса, тангенса

и котангенса и их графики

14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК

Т а б л и ц а 21

График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:

1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями

координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее

З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох

(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордина-

та соответствующей точки единичной окружности

(рис. 79). Поскольку ординату можно найти для

любой точки единичной окружности (в силу того,

что через любую точку окружности всегда можно

провести единственную прямую, перпендикуляр-

ную оси ординат), то область определения функции

y = sin x — все действительные числа. Это можно за-

писать так: D (sin x) = R.

Для точек единичной окружности ординаты нахо-

дятся в промежутке [–1; 1] и принимают все значения

от –1 до 1, поскольку через любую точку отрезка [–1; 1]

оси ординат (который является диаметром единичной

окружности) всегда можно провести прямую, перпендикулярную оси орди-

нат, и получить точку окружности, которая имеет рассматриваемую орди-

нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].

Это можно записать так: E (sin x) = [–1; 1].

Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окружности является точка A, то есть при

Наименьшее значение функции sin x равно минус единице. Это значение

достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть

при

Как было показано в § 13, синус — нечетная функция: sin(-x)= — sin x,

поэтому ее график симметричен относительно начала координат.

В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом

T = 2π: sin (x + 2π) = sin x , таким образом, через промежутки длиной 2π вид графика функции sin x повторя-

ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной 2 π , а

потом полученную линию парал лельно перенести вправо и влево вдоль оси Ox на расстояние kT = 2πk , где

k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых sin x, то есть ордината соответствующей точки единичной окруж­

ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-

ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).

Промежутки знакопостоянства . Как было обосновано в § 13, значения

функции синус положительны (то есть ордината соответствующей точки

единичной окружности положительна) в I и II четвертях (рис. 80). Таким

образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех

x ∈ (2πk; π + 2πk), k ∈ Z.

Значения функции синус отрицательны (то есть ордината соответствую-

щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-

Промежутки возрастания и убывания

Учитывая периодичность функции sin x с периодом T = 2π, достаточно

исследовать ее на возрастание и убывание на любом промежутке длиной

2π, например на промежутке

то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной окружности увеличивается (то есть

sin x ₂ > sin x ₁ ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,

делаем вывод, что она такж е возрастает на каждом из промежутков

Если x ∈ (рис. 81, б), то при увеличении аргумента x (x ₂ > x ₁ ) ордината соответствующей точки единичной

окружности уменьшается (то есть sin x _{2 1} ), таким образом, на этом промежутке функция sin x убывает. Учитывая

периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой

функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на

промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината

соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на

промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для

построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат

Поскольку мы построили график на

промежутке длиной 2π, то, учитывая

периодичность синуса (с периодом 2π),

повторяем вид графика на каждом про-

межутке длиной 2π (то есть переносим па-

раллельно график вдоль оси Ох на 2πk,

где k — целое число).

Получаем график, который называется

З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,

множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,

описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими

колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль

координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией

времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная

фаза,

14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что значение косинуса — это абсцис-

са соответствующей точки единичной окружности

(рис. 85). Поскольку абсциссу можно найти для лю-

бой точки единичной окружности (в силу того, что

через любую точку окружности, всегда можно про-

вести единственную прямую, перпендикулярную оси

абсцисс), то область определения функции y = cos x —

все действительные числа. Это можно записать так:

D (cos x) = R.

Для точек единичной окружности абсциссы нахо-

дятся в промежутке [–1; 1] и принимают все значе-

ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной

всегда можно провести прямую, перпендикулярную оси абсцисс, и получить

точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:

y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это

зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при

x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда

соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.

Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси

Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом

T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.

Чтобы найти точки пересечения графика функции с осями координат , напомним, что на оси Oy значение x = 0. Тогда

соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при

которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только

тогда, когда на единичной окружности будут выбраны точки C или D, то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции косинус положительны (то есть абсцисса соответствующей точки

единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-

тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех

Значения функции косинус отрицательны (то есть абсцисса соответству-

ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,

поэтому cos x

Промежутки возрастания и убывания

Учитывая периодичность функции cos x (T = 2π), достаточно исследовать

ее на возрастание и убывание на любом промежутке длиной 2π, например

на промежутке [0; 2π].

Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x ₂ > x ₁ ) абсцисса соответствующей точки единичной

окружности уменьшается (то есть cos x _{2 1} ), следовательно, на этом промежутке функция cos x убывает. Учитывая

периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.

Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x ₂ > x ₁ ) аб-

сцисса соответствующей точки единичной окружности увеличивается (то

есть cos x ₂ >cos x ₁ ), таким образом, на этом промежутке функция cos x

возрастает. Учитывая периодичность функции cos x, делаем вывод, что

она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.

Проведенное исследование позволяет построить график функции y = cos x

аналогично тому, как был построен график функ-

ции y = sin x. Но график функции у = cos x можно

также получить с помощью геометрических преоб-

разований графика функции у = sin х, используя

Эту формулу можно обосновать, например, так.

Рассмотрим единичную окружность (рис. 88), отметим на ней точки

🌟 Видео

График функции y=sinx и ее свойства. 10 класс.Скачать

10 класс, 22 урок, Простейшие тригонометрические уравнения неравенстваСкачать

Тригонометрические уравнения. Алгебра 10 класс. cos x = a.Скачать

Область определения тригонометрических функцийСкачать