Любые два прямоугольных треугольника равны

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

СРОЧНО ПОЖАЛУЙСТА♥3
1)Два треугольника называются подобными, если их углы соответственно равны
1) да ; 2) нет

2)Любые два прямоугольных и равнобедренных треугольника подобны.
1) нет ;2) да

3)Любые два прямоугольных треугольника подобны.
1) да 2) нет

4)Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника, то такие треугольники подобны
1) да ; 2) нет

5)Если два треугольника подобны, то их соответствующие стороны равны
1) да; 2) нет

6)Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
1) да ; 2) нет

7)Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники подобны.
1) да ; 2) нет

8)Если два угла одного треугольника соответственно пропорциональны двум углам другого треугольника, то такие треугольники подобны.
1) да ; 2) нет

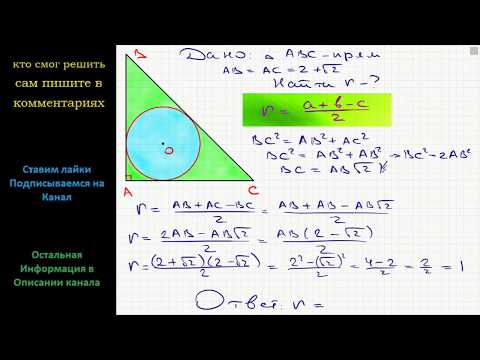
Видео:Геометрия Катеты равнобедренного прямоугольного треугольника равны 2+√2. Найдите радиус окружностиСкачать

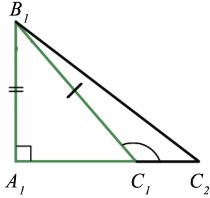
Любые два прямоугольных треугольника равны

Какие из следующих утверждений верны?

1) Любые два прямоугольных треугольника подобны.

2) Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.

3) Стороны треугольника пропорциональны косинусам противолежащих углов.

4) Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Если утверждений несколько, запишите их номера в порядке возрастания.

Проверим каждое из утверждений.

1) «Любые два прямоугольных треугольника подобны.» — неверно, так как нет второго равного угла.

2) «Если катет и гипотенуза прямоугольного треугольника равны соответственно 6 и 10, то второй катет этого треугольника равен 8.» — верно, по теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов.

3) «Стороны треугольника пропорциональны косинусам противолежащих углов.» — неверно, по теореме синусов стороны треугольника пропорциональны синусам противолежащих сторон.

4) «Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.» — верно, по теореме косинусов.

Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Признаки равенства прямоугольных треугольников

Признаки равенства прямоугольных треугольников позволяют сравнивать прямоугольные треугольники лишь по двум элементам, так как любые два прямых угла равны.

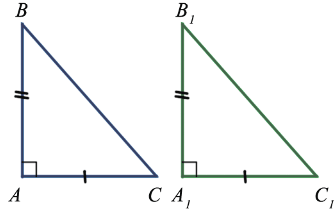
1. Признак равенства по двум катетам

Данный признак следует из первого признака равенства треугольников.

Пример:

ABC = A₁B₁C₁, т.к. AB = A₁B₁ и AC = A₁C₁.

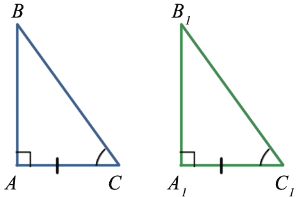
2. Признак равенства по катету и острому углу

Данный признак следует из второго признака равенства треугольников.

Пример:

ABC = A₁B₁C₁, т.к. AC = A₁C₁, C = C₁

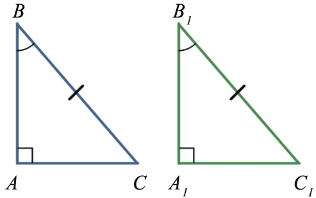
3. Признак равенства по гипотенузе и острому углу

Теорема

Пример:

ABC = A₁B₁C₁, т.к. BC = B₁C₁, B = B₁

Доказательство

Так как сумма двух острых углов прямоугольного треугольника равна 90 0 , то в таких треугольниках два других острых угла также равны, поэтому данные треугольники равны по второму признаку треугольников, т.е. по стороне(по гипотенузе) и двум прилежащим к ней углам, что и требовалось доказать.

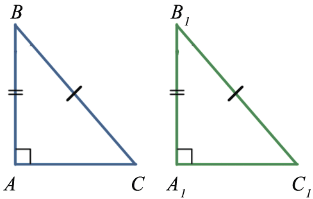
4. Признак равенства по катету и гипотенузе

Теорема

Пример:

ABC = A₁B₁C₁, т.к. BC = B₁C₁, AB = A₁B₁

Доказательство

Дано: ABC, A₁B₁C₁, BC = B₁C₁, AB = A₁B₁

Доказать: ABC = A₁B₁C₁

Доказательство:

Рассмотрим данные треугольники:

Так как A = A₁, то ABC можно наложить на A₁B₁C₁ так, что вершина A совместится с вершиной A₁, а стороны AC и AB наложатся соответственно на лучи A₁C₁ и A₁B₁. При этом вершина B совместится с вершиной B₁, потому что AB = A₁B₁. Но тогда вершина C также совместится с вершиной C₁. Действительно, если предположить, что точка C совместится с некоторой другой точкой C₂ луча A₁C₁, то получим равнобедренный треугольник C₁B₁C₂.

В C₁B₁C₂ углы при основании не равны (C₂ — острый, а C₁ — тупой, так как он смежный с углом B₁C₁A₁, который является острым). А это невозможно, так как у равнобедренного треугольника углы у основания равны, следовательно, вершина C совместится с вершиной C₁. А это значит, что полностью совместятся треугольники ABC, A₁B₁C₁, т.е. они равны, что и требовалось доказать.

Поделись с друзьями в социальных сетях:

🎥 Видео

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

1710 два катета прямоугольного треугольника равны 8 и 7 найдите площадь этого треугольникаСкачать

Свойства прямоугольного треугольника. 7 класс.Скачать

Признаки равенства треугольников. 7 класс.Скачать

Катеты прямоугольного треугольника равны 3 и 4. Найдите высоту, проведённую к гипотенузеСкачать

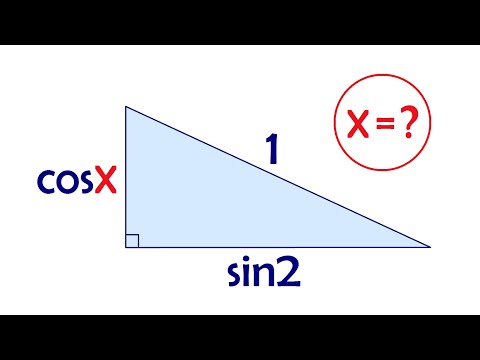
Катеты прямоугольного треугольника равны cosx и sin2. Найдите x, если гипотенуза равна 1Скачать

36. Признаки равенства прямоугольных треугольниковСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

Геометрия 7. Урок 9 - Признаки равенства прямоугольных треугольниковСкачать

Прямоугольный треугольник. Признаки равенства прямоугольных треугольников - 7 класс геометрияСкачать

Высота в прямоугольном треугольнике. 8 класс.Скачать

1728 катеты прямоугольного треугольника равны 9 и 40 найдите гипотенузу этого треугольникаСкачать

Найти радиус равнобедренного прямоугольного треугольника 3 задание проф. ЕГЭ по математикеСкачать

Задача 6 №27932 ЕГЭ по математике. Урок 146Скачать

Признаки равенства прямоугольного треугольника | Геометрия 7-9 класс #36 | ИнфоурокСкачать

КАТЕТЫ И ВЫСОТА В ПРЯМОУГОЛЬНОМ ТРЕУГОЛЬНИКЕ ЧАСТЬ I #математика #егэ #огэ #Shorts #геометрияСкачать

Профильный ЕГЭ 2024. Задача 1. Прямоугольный треугольник. 10 классСкачать