- Условие
- Все решения
- Касательная в точке a к описанной окружности треугольника abc
- Описанная окружность около треугольника и касательная к нему
- Please wait.
- We are checking your browser. mathvox.ru
- Why do I have to complete a CAPTCHA?
- What can I do to prevent this in the future?
- Окружность, описанная около треугольника. Треугольник, вписанный в окружность. Теорема синусов
- Серединный перпендикуляр к отрезку
- Окружность, описанная около треугольника
- Свойства описанной около треугольника окружности. Теорема синусов
- Доказательства теорем о свойствах описанной около треугольника окружности
- Касательная к окружности
- Касательная к окружности, секущая и хорда — в чем разница
- Свойства касательной к окружности
- Задача
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- Задача 1
- Задача 2
- 🔍 Видео
Условие
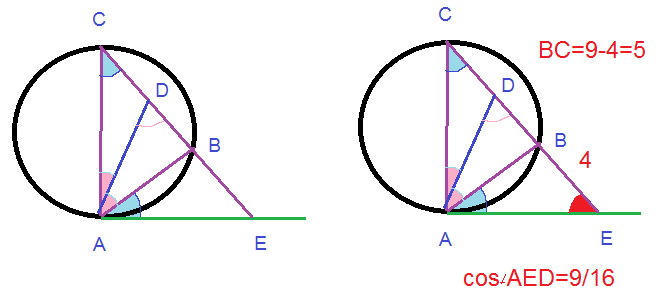
16. Касательная в точке А к описанной окружности треугольника АВС пересекает прямую ВС в точке Е, AD — биссектриса треугольника АВС.
А) Докажите, что АЕ=ЕD
Б) Известно, что точка Е лежит на луче СВ и СЕ=9, ВЕ=4, cos AED = 9/16. Найдите расстояние от вершины В до прямой АС.
Все решения
а)
∠ АСB — вписанный в окружность, он измеряется половиной дуги АС.
∠ ЕАB — угол между касательной АЕ и хордой АВ, измеряется половиной дуги АС.
Значит ∠ АСB= ∠ ЕАB= альфа.
∠ СAD= ∠ BAD = бета ( АD биссектриса ∠ ВАС)
∠ ЕАD= ∠ЕАВ + ВAD= [b]альфа + бета[/b]
∠ АDE=∠ DАВ+ ∠СAD=[b]альфа + бета[/b] ( внешний угол треугольника АСD.
∠ ЕАD=∠ АDE=альфа + бета
Значит треугольник ЕАD равнобедренный,
[b] АЕ=ЕD.[/b]
б)
CE*BE=AE^2 — [b] произведение секущей на ее внешнюю часть равно квадрату касательной [/b]
9*4=AE^2
AE=6
По теореме косинусов из треугольника АВЕ
АВ^2=АЕ^2+BE^2-2*AE*BE*cos∠ AEB=6^2+4^2-2*6*4*(9/16)=52-27=25
AB=5
По теореме косинусов из треугольника АCЕ
АC^2=АЕ^2+CE^2-2*AE*CE*cos∠ AEB=6^2+9^2-2*6*9*(9/16)=117-(243/4)=225/4
AC=15/2=7,5
Треугольник АВС равнобедренный
АВ=ВС=5
ВК ⊥ АС
Высота ВК равнобедренного треугольника одновременно и медиана.
АК=КС=15/4
По теореме Пифагора
ВК^2=AB^2-AK^2=5^2-(15/4)^2=(400-225)/16=175/16
h=BK=5sqrt(7)/4
О т в е т. 5sqrt(7)/4
Видео:САМЫЙ СТРАННЫЙ ПРИМЕР 3 задания проф. ЕГЭ по математикеСкачать

Касательная в точке a к описанной окружности треугольника abc
2021-08-20 
Теорема Паскаля для треугольника. Докажите, что касательные к описанной окружности треугольника, проведённые в его вершинах, пересекают прямые, содержащие противоположные стороны, в точках, лежащих на одной прямой.
Первый способ. Пусть касательные к описанной окружности треугольника $ABC$, проходящие через точки $A$, $B$ и $C$, пересекаются с прямыми $BC$, $AC$ и $AB$ в точках $A_$, $B_$ и $C_$ соответственно. Тогда
(см. задачу 3991). Перемножив эти равенства, получим, что
Следовательно, по теореме Менелая (см. задачу 5231) точки $A_$, $B_$ и $C_$ лежат на одной прямой.
Второй способ. Пусть касательная, проведённая в точке $A$ к окружности, описанной около неравнобедренного треугольника $ABC$, пересекает прямую $BC$ в точке $A_$. Аналогично определим точки $B_$ и $C_$. Обозначим $angle BAC=alpha$, $angle ABC=beta$, $angle ACB=gamma$. Воспользуемся тригонометрической формой теоремы Менелая.
Рассмотрим случай, изображённый на рисунке. По теореме об угле между касательной и хордой
Следовательно, по теореме Менелая в тригонометрической форме (см. задачу 5355) точки $A_$, $B_$ и $C_$ лежат на одной прямой.
Аналогично для любого другого случая.
Видео:Решение задачи №1 из ЕГЭ математикаСкачать
Описанная окружность около треугольника и касательная к нему
Видео:Геометрия К окружности, описанной около треугольника ABC, проведена в точке B касательнаяСкачать

Please wait.
Видео:2031 окружность центром в точке О описана около равнобедренного треугольника ABCСкачать

We are checking your browser. mathvox.ru
Видео:Геометрия Биссектриса CM треугольника ABC делит сторону AB на отрезки AM = 17 и MB = 19. КасательнаяСкачать
Why do I have to complete a CAPTCHA?
Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

What can I do to prevent this in the future?
If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.
If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.
Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.
Cloudflare Ray ID: 6d5b359f9fa77b33 • Your IP : 85.95.179.65 • Performance & security by Cloudflare
Видео:Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

Окружность, описанная около треугольника.
Треугольник, вписанный в окружность. Теорема синусов
 Серединный перпендикуляр к отрезку Серединный перпендикуляр к отрезку |
 Окружность описанная около треугольника Окружность описанная около треугольника |
 Свойства описанной около треугольника окружности. Теорема синусов Свойства описанной около треугольника окружности. Теорема синусов |
 Доказательства теорем о свойствах описанной около треугольника окружности Доказательства теорем о свойствах описанной около треугольника окружности |
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Серединный перпендикуляр к отрезку
Определение 1 . Серединным перпендикуляром к отрезку называют, прямую, перпендикулярную к этому отрезку и проходящую через его середину (рис. 1).
Теорема 1 . Каждая точка серединного перпендикуляра к отрезку находится на одном и том же расстоянии от концов этого отрезка.
Доказательство . Рассмотрим произвольную точку D , лежащую на серединном перпендикуляре к отрезку AB (рис.2), и докажем, что треугольники ADC и BDC равны.
Действительно, эти треугольники являются прямоугольными треугольниками, у которых катеты AC и BC равны, а катет DC является общим. Из равенства треугольников ADC и BDC вытекает равенство отрезков AD и DB . Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1) . Если точка находится на одном и том же расстоянии от концов отрезка, то она лежит на серединном перпендикуляре к этому отрезку.
Доказательство . Докажем теорему 2 методом «от противного». С этой целью предположим, что некоторая точка E находится на одном и том же расстоянии от концов отрезка, но не лежит на серединном перпендикуляре к этому отрезку. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точки E и A лежат по разные стороны от серединного перпендикуляра (рис.3). В этом случае отрезок EA пересекает серединный перпендикуляр в некоторой точке, которую мы обозначим буквой D .
Докажем, что отрезок AE длиннее отрезка EB . Действительно,
Таким образом, в случае, когда точки E и A лежат по разные стороны от серединного перпендикуляра, мы получили противоречие.
Теперь рассмотрим случай, когда точки E и A лежат по одну сторону от серединного перпендикуляра (рис.4). Докажем, что отрезок EB длиннее отрезка AE . Действительно,
Полученное противоречие и завершает доказательство теоремы 2
Видео:2184 касательная в точках A и B к окружности с центром О пересекаютсяСкачать

Окружность, описанная около треугольника
Определение 2 . Окружностью, описанной около треугольника , называют окружность, проходящую через все три вершины треугольника (рис.5). В этом случае треугольник называют треугольником, вписанным в окружность, или вписанным треугольником .
Видео:Задание 26 ОГЭ по математике #29Скачать

Свойства описанной около треугольника окружности. Теорема синусов
| Фигура | Рисунок | Свойство |
| Серединные перпендикуляры к сторонам треугольника |  | Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке. Посмотреть доказательство |
| Окружность, описанная около треугольника |  | Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника. Посмотреть доказательство |
| Центр описанной около остроугольного треугольника окружности | Центр описанной около остроугольного треугольника окружности лежит внутри треугольника. | |
| Центр описанной около прямоугольного треугольника окружности |  | Центром описанной около прямоугольного треугольника окружности является середина гипотенузы. Посмотреть доказательство |
| Центр описанной около тупоугольного треугольника окружности |  | Центр описанной около тупоугольного треугольника окружности лежит вне треугольника. |
| Теорема синусов |  |
Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
| Серединные перпендикуляры к сторонам треугольника |
 |
Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.

Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.

Центр описанной около остроугольного треугольника окружности лежит внутри треугольника.

Центром описанной около прямоугольного треугольника окружности является середина гипотенузы.

Центр описанной около тупоугольного треугольника окружности лежит вне треугольника.

Для любого треугольника справедливы равенства (теорема синусов):

где a , b , c – стороны треугольника, A , B , С – углы треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где A , B , С – углы треугольника, S – площадь треугольника, R – радиус описанной окружности.

Для любого треугольника справедливо равенство:
где a , b , c – стороны треугольника, S – площадь треугольника, R – радиус описанной окружности.
Видео:8 класс, 32 урок, Касательная к окружностиСкачать

Доказательства теорем о свойствах описанной около треугольника окружности
Теорема 3 . Все серединные перпендикуляры, проведённые к сторонам произвольного треугольника, пересекаются в одной точке.
Доказательство . Рассмотрим два серединных перпендикуляра, проведённых к сторонам AC и AB треугольника ABC , и обозначим точку их пересечения буквой O (рис. 6).
Поскольку точка O лежит на серединном перпендикуляре к отрезку AC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на серединном перпендикуляре к отрезку AB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на серединном перпендикуляре к отрезку BC. Таким образом, все три серединных перпендикуляра проходят через одну и ту же точку, что и требовалось доказать.
Следствие . Около любого треугольника можно описать окружность. Центром описанной около треугольника окружности является точка, в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника.
Доказательство . Рассмотрим точку O , в которой пересекаются все серединные перпендикуляры, проведённые к сторонам треугольника ABC (рис. 6).
При доказательстве теоремы 3 было получено равенство:
из которого вытекает, что окружность с центром в точке O и радиусами OA , OB , OC проходит через все три вершины треугольника ABC , что и требовалось доказать.
Теорема 4 (теорема синусов) . Для любого треугольника (рис. 7)

Доказательство . Докажем сначала, что длина хорды окружности радиуса R хорды окружности радиуса R , на которую опирается вписанный угол величины φ , вычисляется по формуле:
| l = 2Rsin φ . | (1) |
Рассмотрим сначала случай, когда одна из сторон вписанного угла является диаметром окружности (рис.8).
Поскольку все вписанные углы, опирающиеся на одну и ту же дугу, равны, то для произвольного вписанного угла всегда найдется равный ему вписанный угол, у которого одна из сторон является диаметром окружности.
Формула (1) доказана.
Из формулы (1) для вписанного треугольника ABC получаем (рис.7):
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Касательная к окружности
О чем эта статья:
Видео:#59. Олимпиадная задача о касательной к окружности!Скачать

Касательная к окружности, секущая и хорда — в чем разница
В самом названии касательной отражается суть понятия — это прямая, которая не пересекает окружность, а лишь касается ее в одной точке. Взглянув на рисунок окружности ниже, несложно догадаться, что точку касания от центра отделяет расстояние, в точности равное радиусу.
Касательная к окружности — это прямая, имеющая с ней всего одну общую точку.
Если мы проведем прямую поближе к центру окружности — так, чтобы расстояние до него было меньше радиуса — неизбежно получится две точки пересечения. Такая прямая называется секущей, а отрезок, расположенный между точками пересечения, будет хордой (на рисунке ниже это ВС ).
Секущая к окружности — это прямая, которая пересекает ее в двух местах, т. е. имеет с ней две общие точки. Часть секущей, расположенная внутри окружности, будет называться хордой.
Видео:Геометрия. ОГЭ по математике. Задание 16Скачать

Свойства касательной к окружности
Выделяют четыре свойства касательной, которые необходимо знать для решения задач. Два из них достаточно просты и легко доказуемы, а вот еще над двумя придется немного подумать. Рассмотрим все по порядку.
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны.
Не будем принимать это на веру, попробуем доказать. Итак, у нас даны:
- окружность с центральной точкой А;
- прямая а — касательная к ней;
- радиус АВ, проведенный к касательной.
Докажем, что касательная и радиус АВ взаимно перпендикулярны, т.е. а ⟂ АВ.
Пойдем от противного — предположим, что между прямой а и радиусом АВ нет прямого угла и проведем настоящий перпендикуляр к касательной, назвав его АС.
В таком случае наш радиус АВ будет считаться наклонной, а наклонная, как известно, всегда длиннее перпендикуляра. Получается, что АВ > АС. Но если бы это было на самом деле так, наша прямая а пересекалась бы с окружностью два раза, ведь расстояние от центра А до нее — меньше радиуса. Но по условию задачи а — это касательная, а значит, она может иметь лишь одну точку касания.
Итак, мы получили противоречие. Делаем вывод, что настоящим перпендикуляром к прямой а будет вовсе не АС, а АВ.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Задача
У нас есть окружность, центр которой обозначен О. Из точки С проведена прямая, и она касается этой окружности в точке А. Известно, что ∠АСО = 28°. Найдите величину дуги АВ.
Мы знаем, что касательная АС ⟂ АО, следовательно ∠САО = 90°.
Поскольку нам известны величины двух углов треугольника ОАС, не составит труда найти величину и третьего угла.
∠АОС = 180° — ∠САО — ∠АСО = 180° — 90° — 28° = 62°
Поскольку вершина угла АОС лежит в центре окружности, можно вспомнить свойство центрального угла — как известно, он равен дуге, на которую опирается. Следовательно, АВ = 62°.
Если провести две касательных к окружности из одной точки, лежащей вне этой окружности, то их отрезки от этой начальной точки до точки касания будут равны.
Докажем и это свойство на примере. Итак, у нас есть окружность с центром А, давайте проведем к ней две касательные из точки D. Обозначим эти прямые как ВD и CD . А теперь выясним, на самом ли деле BD = CD.
Для начала дополним наш рисунок, проведем еще одну прямую из точки D в центр окружности. Как видите, у нас получилось два треугольника: ABD и ACD . Поскольку мы уже знаем, что касательная и радиус к ней перпендикулярны, углы ABD и ACD должны быть равны 90°.
Итак, у нас есть два прямоугольных треугольника с общей гипотенузой AD. Учитывая, что радиусы окружности всегда равны, мы понимаем, что катеты AB и AC у этих треугольников тоже одинаковой длины. Следовательно, ΔABD = ΔACD (по катету и гипотенузе).. Значит, оставшиеся катеты, а это как раз наши BD и CD (отрезки касательных к окружности), аналогично равны.
Важно: прямая, проложенная из стартовой точки до центра окружности (в нашем примере это AD), делит угол между касательными пополам.
Задача 1
У нас есть окружность с радиусом 4,5 см. К ней из точки D, удаленной от центра на 9 см, провели две прямые, которые касаются окружности в точках B и C. Определите градусную меру угла, под которым пересекаются касательные.
Решение
Для этой задачи вполне подойдет уже рассмотренный выше рисунок окружности с радиусами АВ и АC. Поскольку касательная ВD перпендикулярна радиусу АВ , у нас есть прямоугольный треугольник АВD. Зная длину его катета и гипотенузы, определим величину ∠BDA.
∠BDA = 30° (по свойству прямоугольного треугольника: угол, лежащий напротив катета, равного половине гипотенузы, составляет 30°).
Мы знаем, что прямая, проведенная из точки до центра окружности, делит угол между касательными, проведенными из этой же точки, пополам. Другими словами:
∠BDC = ∠BDA × 2 = 30° × 2 = 60°
Итак, угол между касательными составляет 60°.
Задача 2
К окружности с центром О провели две касательные КМ и КN. Известно, что ∠МКN равен 50°. Требуется определить величину угла ∠NМК.
Решение
Согласно вышеуказанному свойству мы знаем, что КМ = КN. Следовательно, треугольник МNК является равнобедренным.
Углы при его основании будут равны, т.е. ∠МNК = ∠NМК.
∠МNК = (180° — ∠МКN) : 2 = (180° — 50°) : 2 = 65°
Соотношение между касательной и секущей: если они проведены к окружности из одной точки, лежащей вне окружности, то квадрат расстояния до точки касания равен произведению длины всей секущей на ее внешнюю часть.
Данное свойство намного сложнее предыдущих, и его лучше записать в виде уравнения.
Начертим окружность и проведем из точки А за ее пределами касательную и секущую. Точку касания обозначим В, а точки пересечения — С и D. Тогда CD будет хордой, а отрезок AC — внешней частью секущей.
Задача 1
Из точки М к окружности проведены две прямые, пусть одна из них будет касательной МA, а вторая — секущей МB. Известно, что хорда ВС = 12 см, а длина всей секущей МB составляет 16 см. Найдите длину касательной к окружности МA.
Решение
Исходя из соотношения касательной и секущей МА 2 = МВ × МС.
Найдем длину внешней части секущей:
МС = МВ — ВС = 16 — 12 = 4 (см)
МА 2 = МВ × МС = 16 х 4 = 64
Задача 2
Дана окружность с радиусом 6 см. Из некой точки М к ней проведены две прямые — касательная МA и секущая МB . Известно, что прямая МB пересекает центр окружности O. При этом МB в 2 раза длиннее касательной МA . Требуется определить длину отрезка МO.
Решение
Допустим, что МО = у, а радиус окружности обозначим как R.
В таком случае МВ = у + R, а МС = у – R.
Поскольку МВ = 2 МА, значит:
МА = МВ : 2 = (у + R) : 2
Согласно теореме о касательной и секущей, МА 2 = МВ × МС.
(у + R) 2 : 4 = (у + R) × (у — R)
Сократим уравнение на (у + R), так как эта величина не равна нулю, и получим:
Поскольку R = 6, у = 5R : 3 = 30 : 3 = 10 (см).
Ответ: MO = 10 см.
Угол между хордой и касательной, проходящей через конец хорды, равен половине дуги, расположенной между ними.
Это свойство тоже стоит проиллюстрировать на примере: допустим, у нас есть касательная к окружности, точка касания В и проведенная из нее хорда AВ. Отметим на касательной прямой точку C, чтобы получился угол AВC.
Задача 1
Угол АВС между хордой АВ и касательной ВС составляет 32°. Найдите градусную величину дуги между касательной и хордой.
Решение
Согласно свойствам угла между касательной и хордой, ∠АВС = ½ АВ.
АВ = ∠АВС × 2 = 32° × 2 = 64°
Задача 2
У нас есть окружность с центром О, к которой идет прямая, касаясь окружности в точке K. Из этой точки проводим хорду KM, и она образует с касательной угол MKB, равный 84°. Давайте найдем величину угла ОMK.
Решение
Поскольку ∠МКВ равен половине дуги между KM и КВ, следовательно:
КМ = 2 ∠МКВ = 2 х 84° = 168°
Обратите внимание, что ОМ и ОK по сути являются радиусами, а значит, ОМ = ОК. Из этого следует, что треугольник ОMK равнобедренный.
∠ОКМ = ∠ОМК = (180° — ∠КОМ) : 2
Так как центральный угол окружности равен угловой величине дуги, на которую он опирается, то:
∠ОМК = (180° — ∠КОМ) : 2 = (180° — 168°) : 2 = 6°
🔍 Видео
ОКРУЖНОСТИ В ОГЭ ✨ #огэ #математика #егэ #геометрия #окружностьСкачать
Задание 26 Свойство касательной и секущей Подобные треугольникиСкачать

Задача по геометрии (ОГЭ, тренировочный вариант)Скачать

ЕГЭ 2017 | Задание 3 | К окружности ... ✘ Школа ПифагораСкачать

Задание В6 по математике.Скачать

Геометрия К окружности, вписанной в треугольник ABC, проведены три касательные (см. рис.)Скачать