Презентация огэ математика окружность

Презентация РР. В презентации рассмотрены решения задач первой части по теме «Окружность».

Видео:РАДИУС вписанной окружности #математика #огэ #огэматематика #данирСкачать

Скачать:

Предварительный просмотр:

Видео:Углы в окружности. 16 задание ОГЭ математика 2023 | Молодой РепетиторСкачать

Подписи к слайдам:

Подготовка к ОГЭ. Окружность.

Хорды АВ и CD окружности пересекаются в точке М. Найдите МА, если МВ = 8 см, МС = 6 см, М D = 4 см. А В С D M A М ∙ МВ = СМ ∙ MD 8 4 6 A М ∙ 8 = 6 ∙ 4 A М = 3

Окружность с центром О касается сторон угла с вершиной А в точках В и С. Найдите угол ВАС, если угол ВОС равен 147. А С В 0 Сумма углов четырехугольника — 360 Радиусы, проведенные в точку касания – перпендикулярны касательной. ВАС = 360 – 90 – 90 – 147 = 33

Точки А и В делят окружность на две дуги, длины которых относятся как 5:7. Найдите величину центрального угла, опирающегося на меньшую из дуг. А В 5х 7х 0 5х + 7х = 360 х = 30 АОВ = 5 ∙ 30 = 150

Радиус окружности равен 15 см. Найдите расстояние от центра окружности до хорды, длина которой равна 18 см. А В С 1 8 15 0 Т.к. ОС АВ, то АС=ВС=9 по т. Пифагора ОС =

Отрезок АВ является хордой окружности с центром О. Найдите угол между прямой АВ и касательной к окружности, проходящей через точку А, если угол АОВ равен 28. А В С 28 0 ОА АС ( как радиус, проведенный в точку касания ) — равнобедренный ( ОА=ОВ – как радиусы одной окружности )

Отрезки АВ и ВС являются соответственно диаметром и хордой окружности с центром О. Найдите угол АОС, если угол ОСВ равен 39. А В 39 0 С — равнобедренный ( ОС=ОВ – как радиусы одной окружности ) или Внешний угол треугольника равен сумме двух углов, не смежных с ним.

Окружность, вписанная в треугольник АВС, касается сторон АВ, ВС и АС в точках М, К и Р соответственно. Найдите периметр треугольника АВС, если АР = 4 см, ВМ = 6 см, СК = 3 см. А В С М К Р 4 3 6 Отрезки касательных, проведенных из одной точки равны. ВМ = ВК АМ = АР СР = СК 6 3 4 АВ = 10 АС = 7 ВС = 9 Р = 10 + 7 + 9 = 26

Найдите диаметр окружности, описанной около прямоугольного треугольника, если синус одного из углов треугольника равен 3/7, а противолежащий этому углу катет равен 15 см. А В С Центр описанной около п /у треугольника окружности лежит на середине гипотенузы. d = AC sinA =3/7 15 sinA = ВС/АС 3/7 = 15/АС АС = 35

Найдите радиус окружности, вписанной в треугольник, если один из углов треугольника равен 120, а расстояние от центра окружности до вершины этого угла равно 18 см. 0 Т.к. в вписанном треугольнике тупой угол, то этот треугольник лежит по одну сторону от центра окружности. А В С 120 ОВ = r = 18

Найдите радиус окружности, описанной около треугольника, если одна из сторон треугольника равна 20 см, а расстояние от центра окружности до этой стороны равно 24 см. 0 А В 20 С 24 Т.к. ОК АС, то АК=КС=10 К по т. Пифагора ОС =

Отрезки АВ и CD являются хордами окружности. Найдите длину хорды CD , если АВ = 10 см, а расстояния от центра окружности до хорд АВ и CD равны соответственно 12 см и 5 см. А В X 1 2 5 0 C D 10 Y АХ = 5 по т. Пифагора ОА = ОА = ОС = 13 по т. Пифагора С Y = CD = 24

Отрезки АВ и BC являются хордами окружности с центром О. Найдите угол АСВ, если угол АВО равен 42. А В 42 0 С АСВ – вписанный угол, АОВ – соответствующий ему центральный АОВ = 180 – 42∙2=96 АОВ= 96 : 2 = 48

В окружность вписан четырехугольник АВС D . Найдите угол АС D , если углы BAD и ADB равны соответственно 73 и 37. А В 37 С D 73 ABD : ABD = 180 – (73 + 37) = 70 АВ D = ACD – как вписанные углы, опирающиеся на одну дугу A С D = 70

Окружность с центром О касается сторон угла с вершиной А, величина которого равна 40, в точках В и С. Найдите углы треугольника ВОС. А С В 0 АОВ – п /у (радиус, проведенный в точку касания, перпендикулярен касательной) АОВ = АОС по катету и гипотенузе (АО – общая, ОВ = ОС = r ) ОАВ = 20 ВОА= 70 ВОС = 140 ОВС = ОСВ = (180 – 140) : 2 = 20

Отрезки АВ и АС являются хордами окружности с центром О. Найдите угол ВАС, если известно, что он является острым и что углы АВО и АСО равны соответственно 23 и 32. А В 23 0 С 32 Угол ВАС – острый, значит его стороны лежат по разные стороны от центра окружности. — равнобедренный — равнобедренный ОАВ = 23 ОАС = 32 ВАС = 23 + 32 = 55

Радиус окружности, описанной около равнобедренного треугольника равен 5 см, а высота, проведенная к основанию, равна 8 см. Найдите площадь треугольника. 0 А В С 5 8 Н Т.к. треугольник р /б, то центр описанной окружности лежите на высоте, проведенной к основанию. ОА = ОВ = R = 5 ОН = 8 – 5 = 3 по т. Пифагора АН = АС = 8 S = ½ ∙ 8 ∙ 8 = 32

Найдите площадь п /у трапеции, боковые стороны которой равны 10 см и 16 см, если известно, что в эту трапецию можно вписать окружность. 10 16 Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. А В С D АВ + CD = ВС + AD = 26 Т.к. трапеция – п /у, то АВ = h S = 130

В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 5 см. 5 А В D С Т.к. в параллелограмм можно вписать окружность, он является ромбом. Р = 4а Р = 4 ∙ 5 = 20

В трапецию, сумма длин боковых сторон которой равна 16 см, вписана окружность. Найдите среднюю линию трапеции. Т.к. в трапецию можно вписать окружность, то суммы противоположных сторон трапеции равны. В С D АВ + CD = ВС + AD = 16 К L = 8 А К L

Видео:ОГЭ 2023. РАЗБОР ЗАДАНИЯ №16 "Окружность"Скачать

По теме: методические разработки, презентации и конспекты

Подготовка к ГИА. Окружность.Центральные и вписанные углы.

Презентация по теме «Окружность.Центральные и вписанные углы» . Материал содержит повторение вопросов теории и задачи для подготовки к ГИА по этой теме.

Презентация к окружному семинару учителей английского языка «Методика подготовки к сдаче ЕГЭ по английскому языку (Письмо часть С2 Эссе)

Подробные поэтапные рекомендации по выполнению части С2 (написание эссе).

6 класс. Задания для подготовки к проверочным работа по теме «Пропорции. Длина окружности и площадь круга»

Материал предназначен для родителей для того, чтобы они могли проконтролировать подготовку детей к различным проверочным работам.

Памятка для подготовки ГИА «Окружность»

Памятка ученикам по теме » Окружность».

Углы,связанные с окружностью. Подготовка к ГИА

Повторяются вписанные и центральные углы, их градусные меры.

Решение задач по теме: «Движение по окружности» Подготовка к ЕГЭ задание «В»

Решение задач по теме «Движение по окружности».

Благодарность за подготовку учащегося к окружному этапу городского конкурса «Ученик года»

Представлена БЛАГОДАРНОСТЬ за подготовку учащегося к окружному этапу городского конкурса «Ученик года -2013».

Видео:Задание на окружность ! #огэ #математика #shortsСкачать

Презентация по математике на тему «Подготовка к ОГЭ. Окружность» (9 класс)

Выбранный для просмотра документ Окружность.pptx

Видео:ОГЭ Математика 24 вариант Ященко 2024Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Окружность (по материалам открытого банка задач ОГЭ по математике) 2018 г. Подготовка к ОГЭ

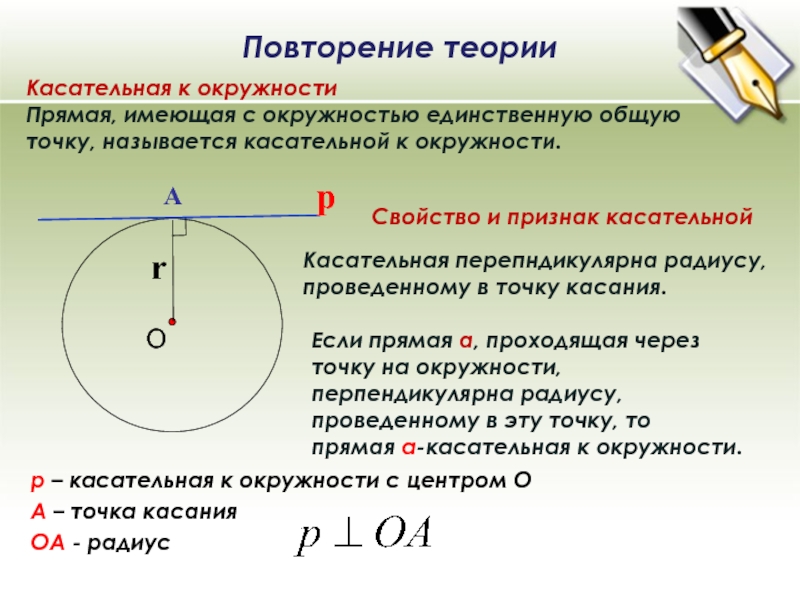
Повторение теории Касательная к окружности Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности. Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая а-касательная к окружности. Касательная перепндикулярна радиусу, проведенному в точку касания. р А р – касательная к окружности с центром О А – точка касания OА — радиус Свойство и признак касательной О r

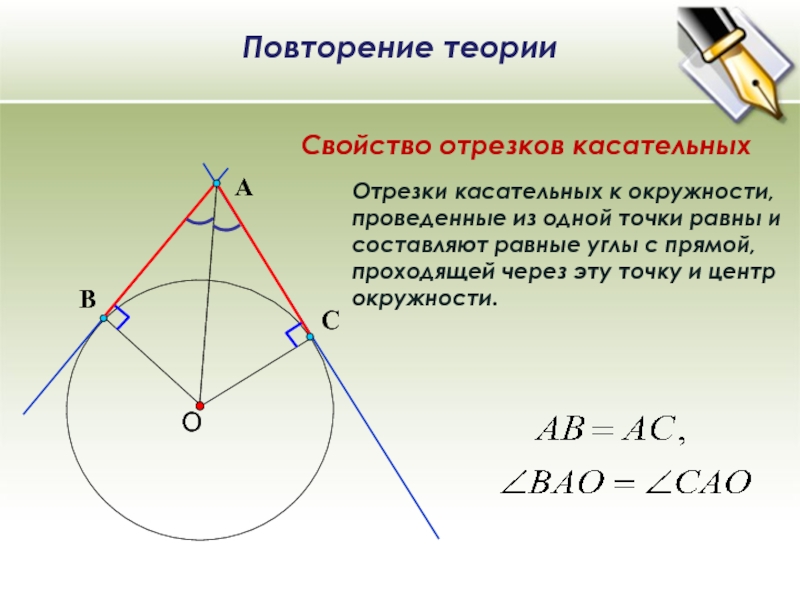
Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. Свойство отрезков касательных Повторение теории О С А В

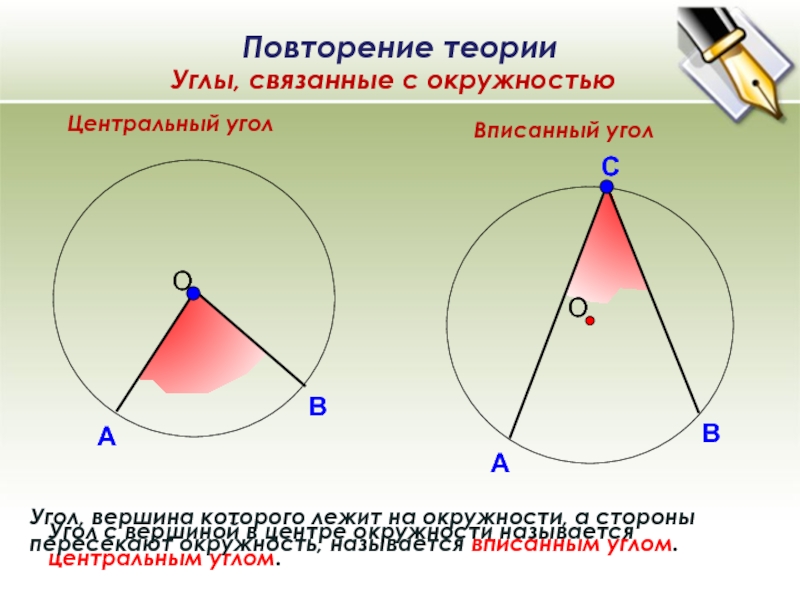
Центральный угол Вписанный угол Угол с вершиной в центре окружности называется центральным углом. Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом. Углы, связанные с окружностью Повторение теории А В С А В О О

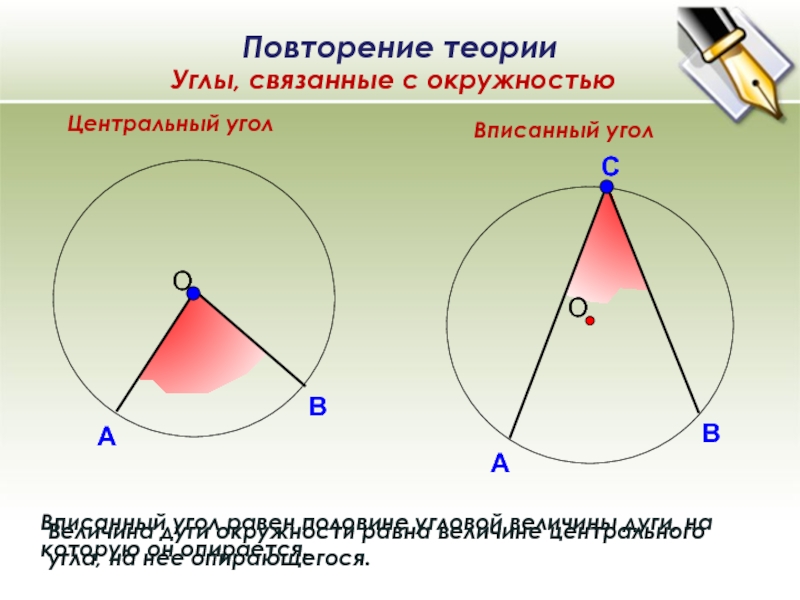
Центральный угол Вписанный угол Величина дуги окружности равна величине центрального угла, на нее опирающегося. Вписанный угол равен половине угловой величины дуги, на которую он опирается. Углы, связанные с окружностью Повторение теории А В С А В О О

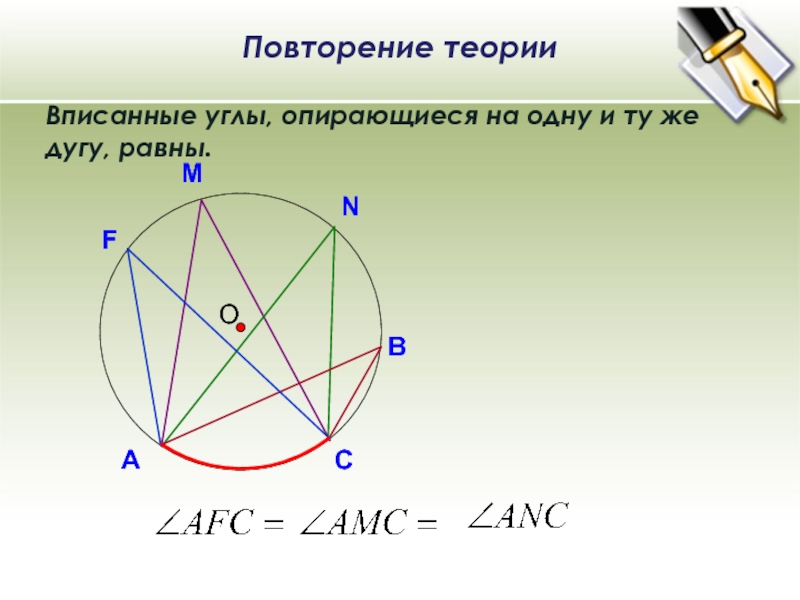
О Вписанные углы, опирающиеся на одну и ту же дугу, равны. В N M Повторение теории А С F

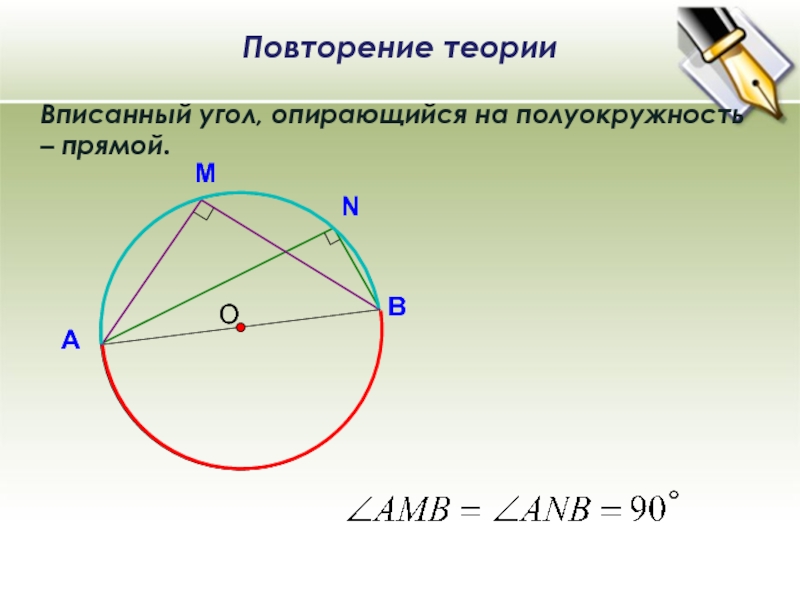
О Вписанный угол, опирающийся на полуокружность – прямой. В А ° Повторение теории N M

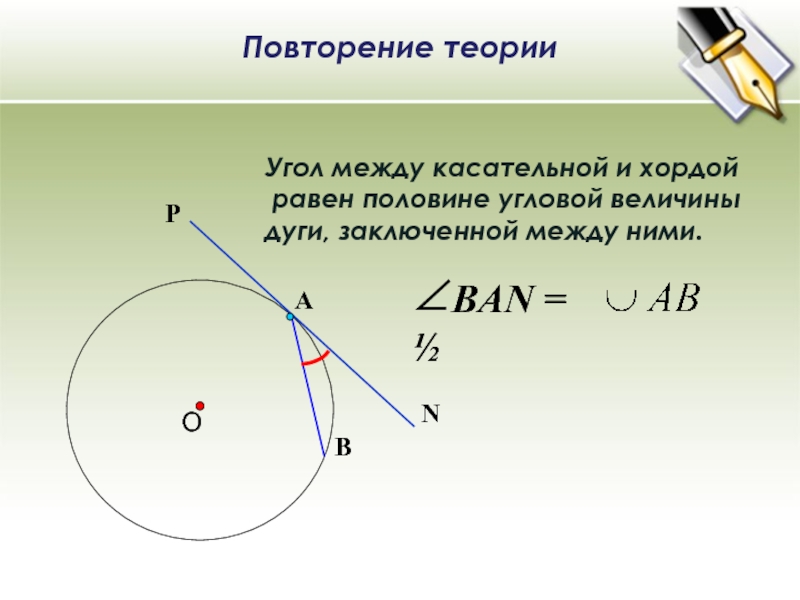
Повторение теории Угол между касательной и хордой равен половине угловой величины дуги, заключенной между ними. ∠BAN = ½ О В Р N А

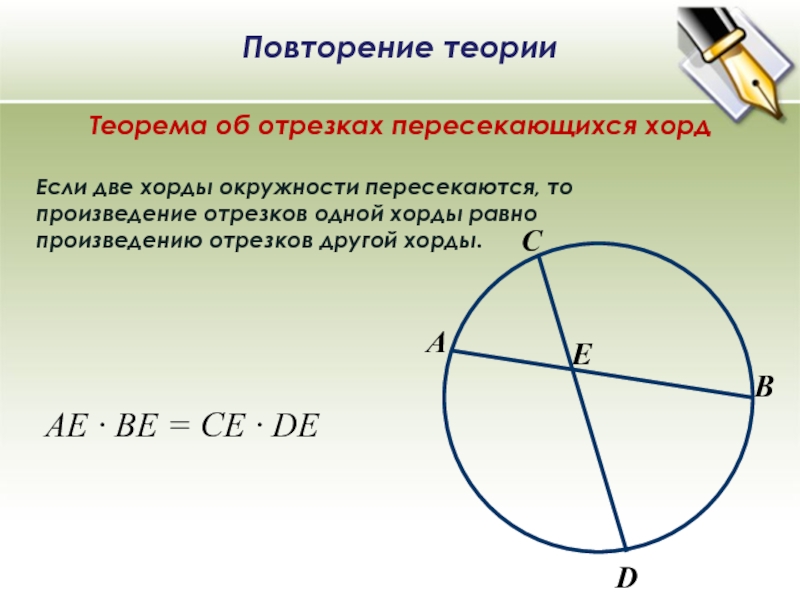
B А C D E Теорема об отрезках пересекающихся хорд Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды. АЕ ∙ ВЕ = СЕ ∙ DE Повторение теории

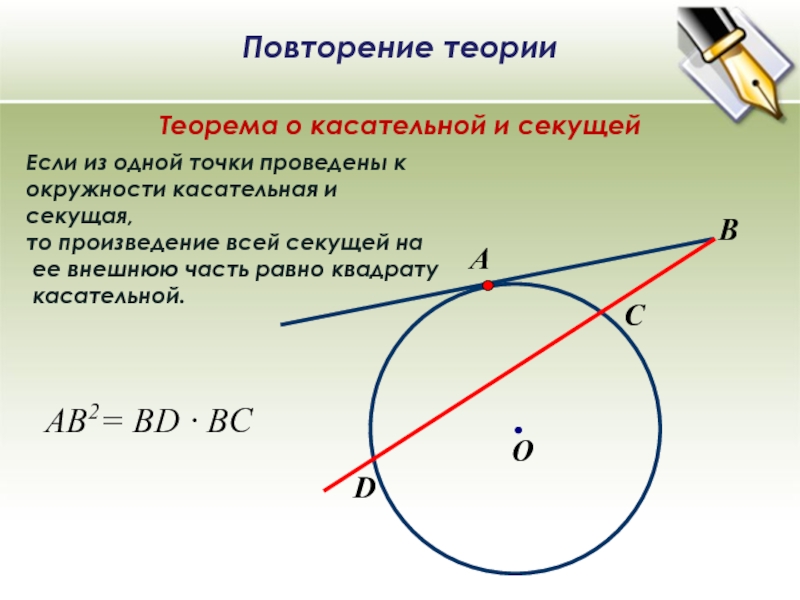
B О А Если из одной точки проведены к окружности касательная и секущая, то произведение всей секущей на ее внешнюю часть равно квадрату касательной. C D AB2= BD ∙ ВC Повторение теории Теорема о касательной и секущей

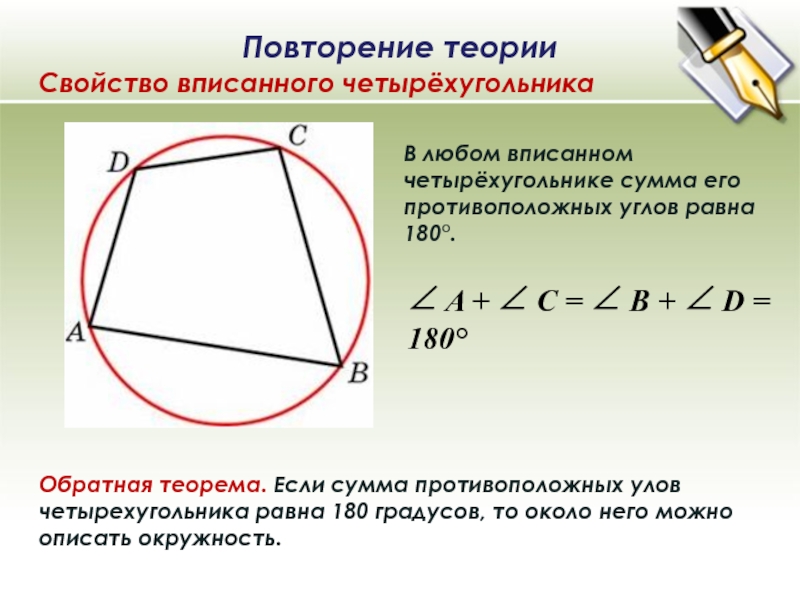
В любом вписанном четырёхугольнике сумма его противоположных углов равна 180°. Обратная теорема. Если сумма противоположных улов четырехугольника равна 180 градусов, то около него можно описать окружность. ∠ A + ∠ C = ∠ B + ∠ D = 180° Повторение теории Свойство вписанного четырёхугольника

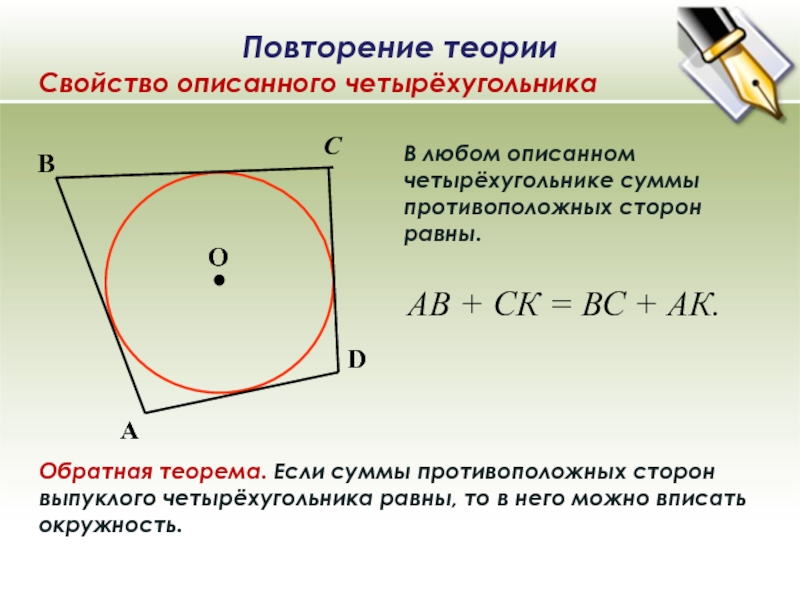
В любом описанном четырёхугольнике суммы противоположных сторон равны. Обратная теорема. Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность. АВ + СК = ВС + АК. Повторение теории Свойство описанного четырёхугольника О

Какие из следующих утверждений верны? 1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу. 2) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность не пересекаются. 3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°. 4) Около всякого треугольника можно описать не более одной окружности. 5) Центром окружности, описанной около треугольника, является точка пересечения биссектрис. Ответ: 1, 3, 4, 6, 8, 9 . 6) Центры вписанной и описанной окружностей равностороннего треугольника совпадают. 7) Около любого ромба можно описать окружность. 8) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника. 9) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

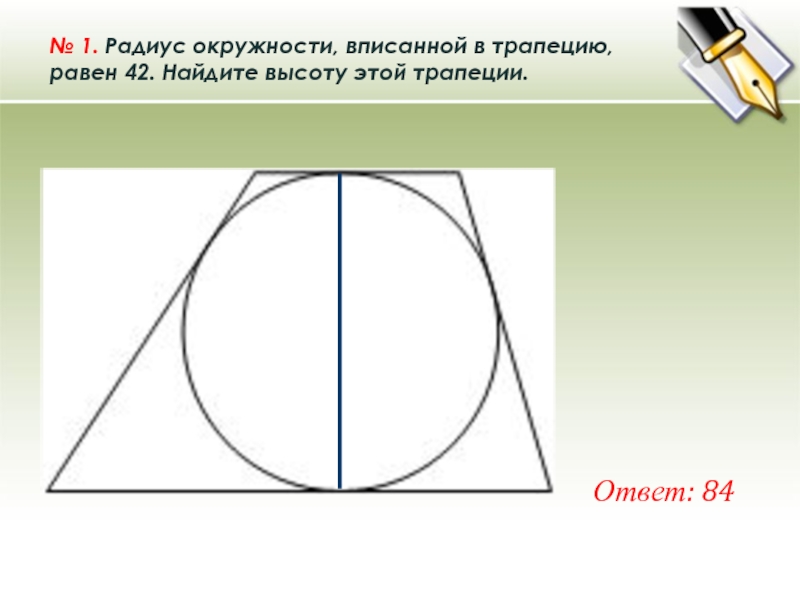
№ 1. Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции. Ответ: 84

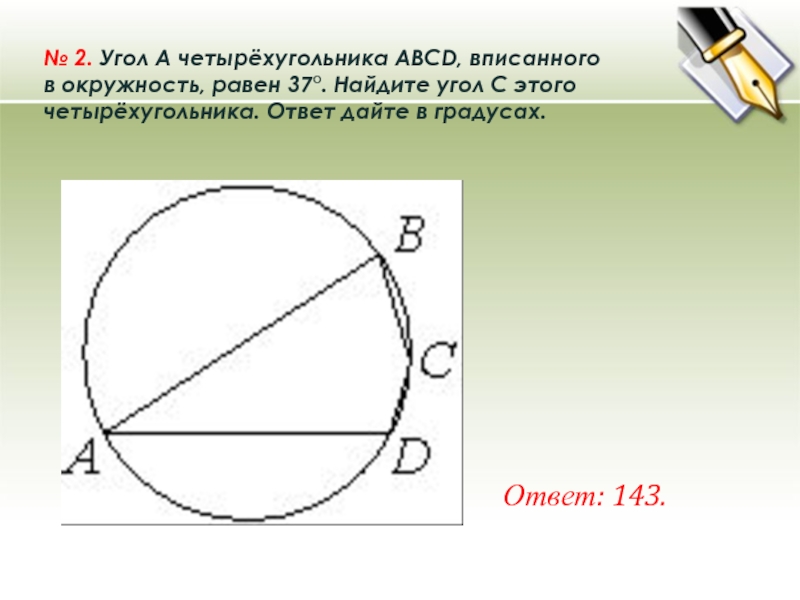
№ 2. Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах. Ответ: 143.

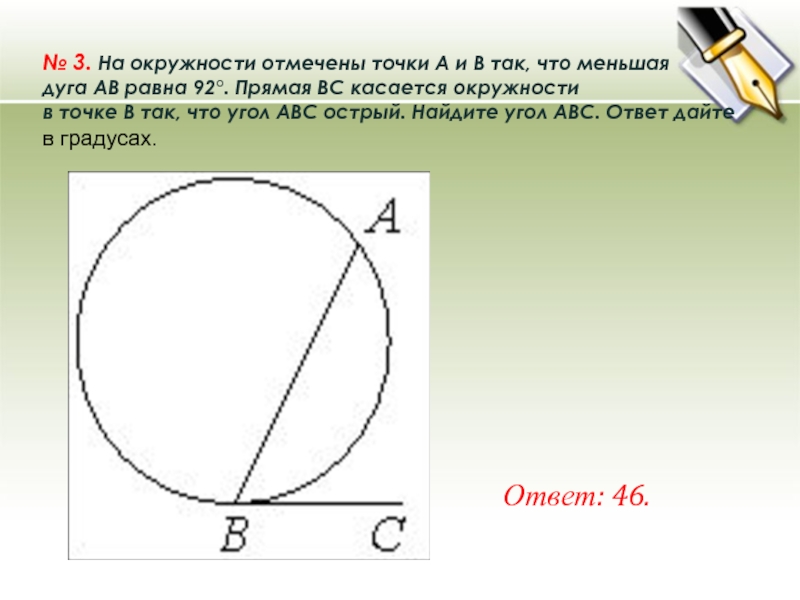
№ 3. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах. Ответ: 46.

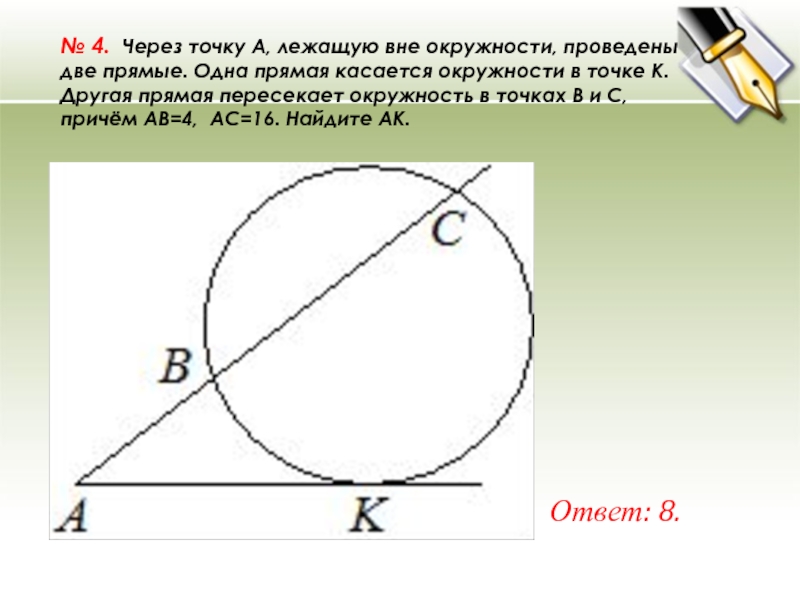
№ 4. Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=16. Найдите AK. Ответ: 8.

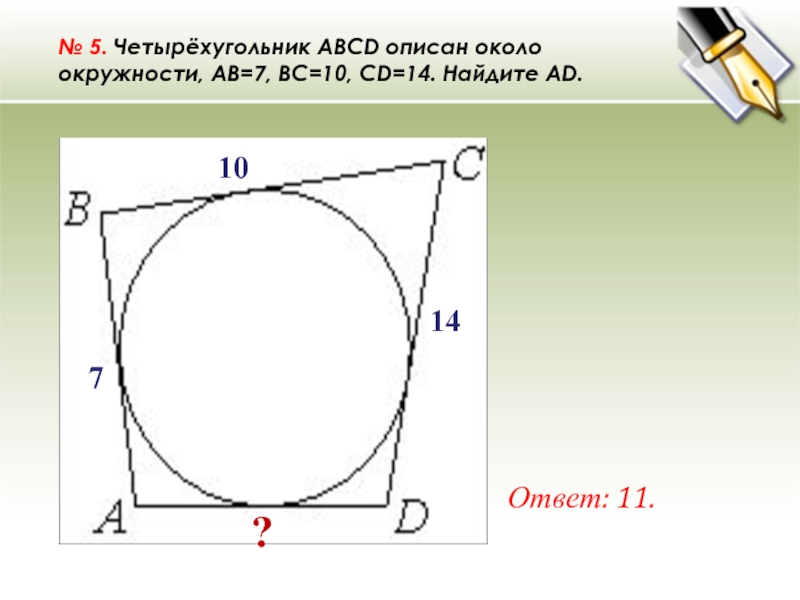
№ 5. Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD. Ответ: 11. ? 14 10 7

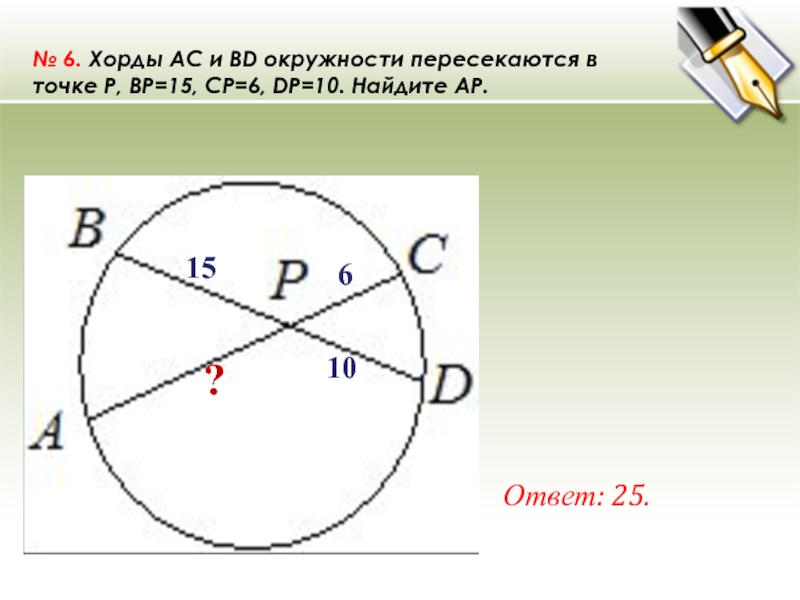
№ 6. Хорды AC и BD окружности пересекаются в точке P, BP=15, CP=6, DP=10. Найдите AP. Ответ: 25. ? 10 6 15

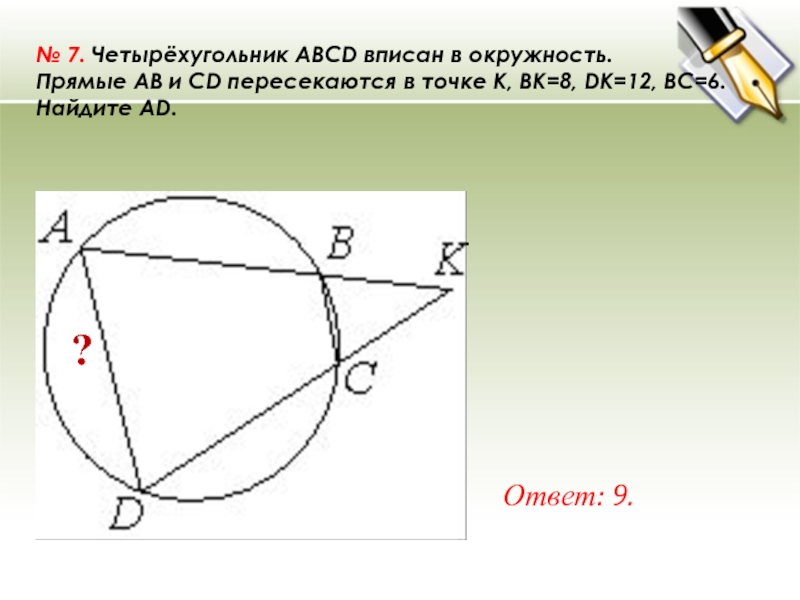
№ 7. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD. Ответ: 9. ?

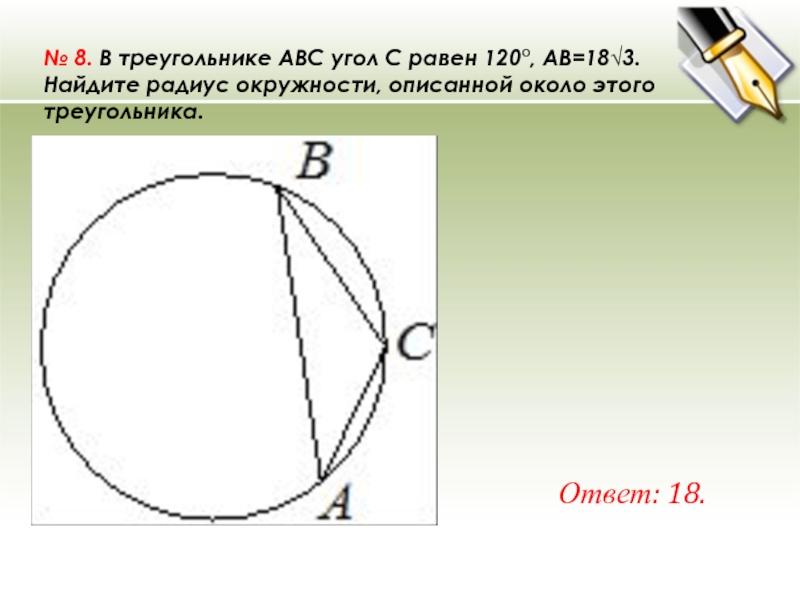
№ 8. В треугольнике ABC угол C равен 120°, AB=18√3. Найдите радиус окружности, описанной около этого треугольника. Ответ: 18.

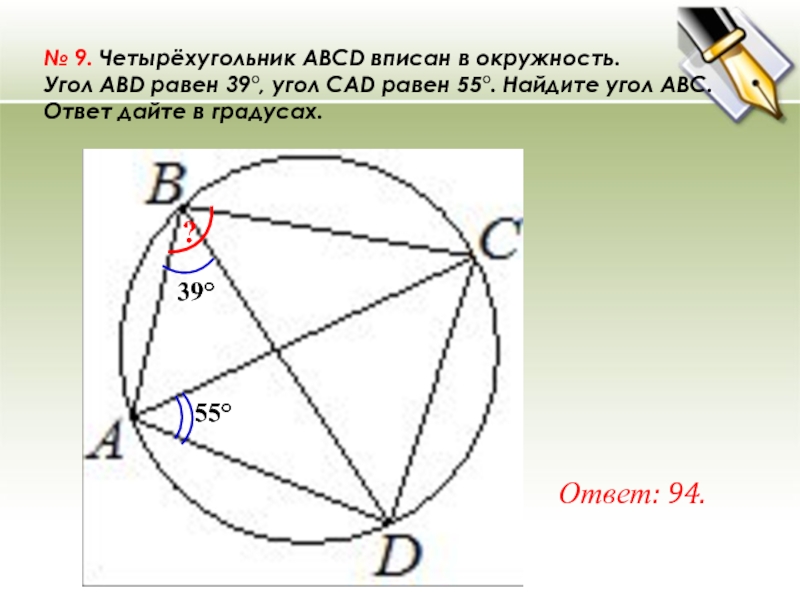
№ 9. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах. Ответ: 94. 39° 55° ?

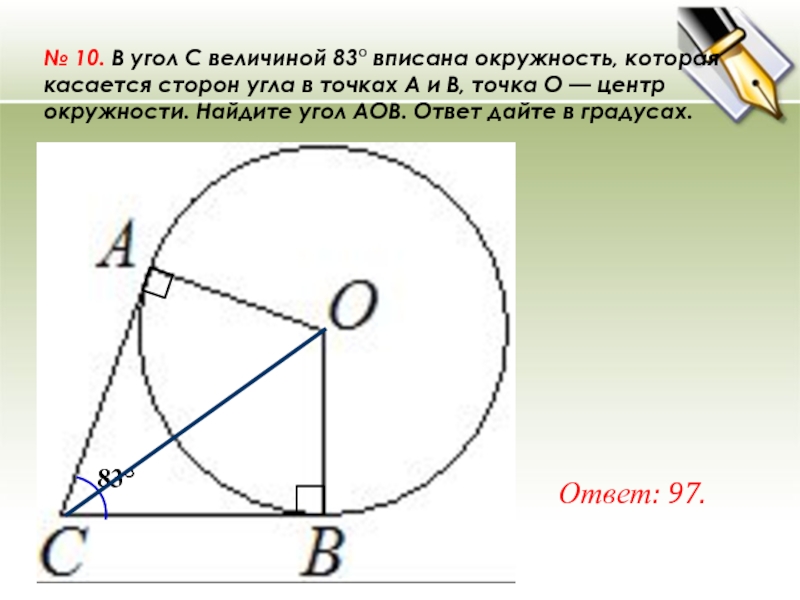
№ 10. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах. Ответ: 97. 83°

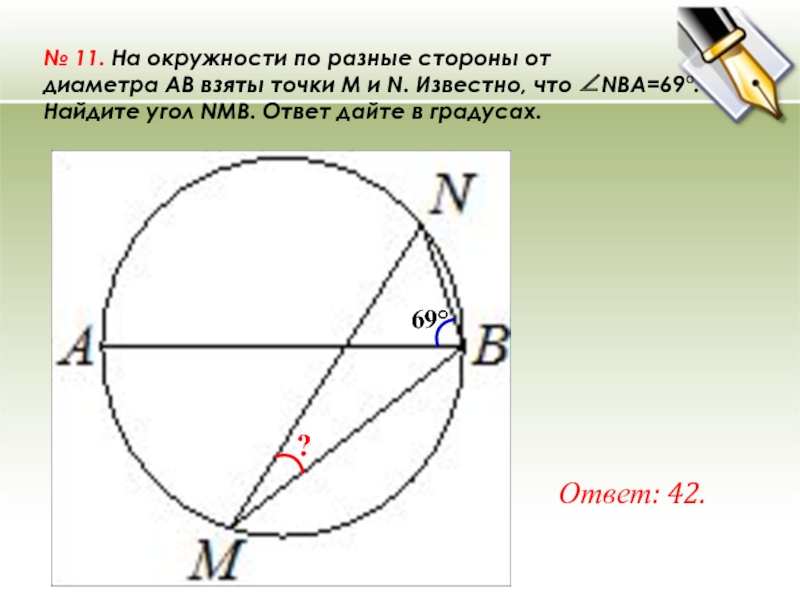
№ 11. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах. Ответ: 42. 69° ?

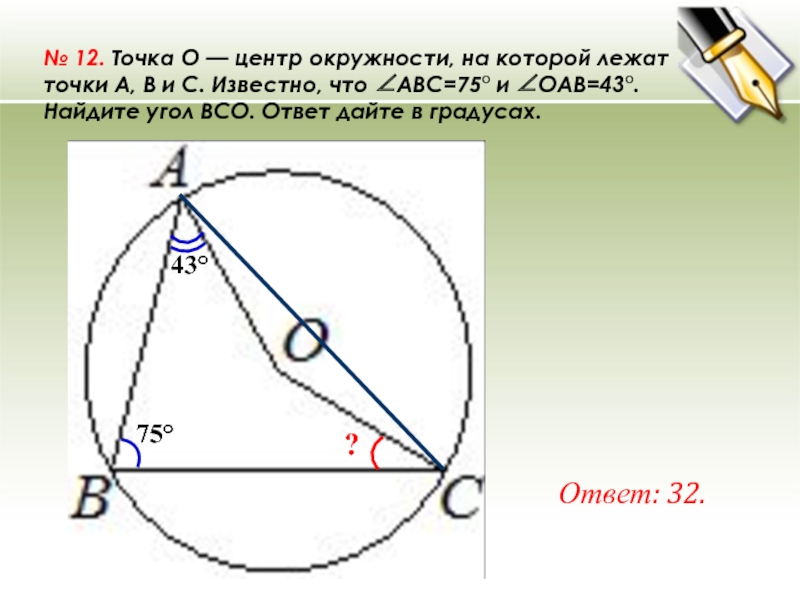
№ 12. Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=43°. Найдите угол BCO. Ответ дайте в градусах. Ответ: 32. 43° ? 75°

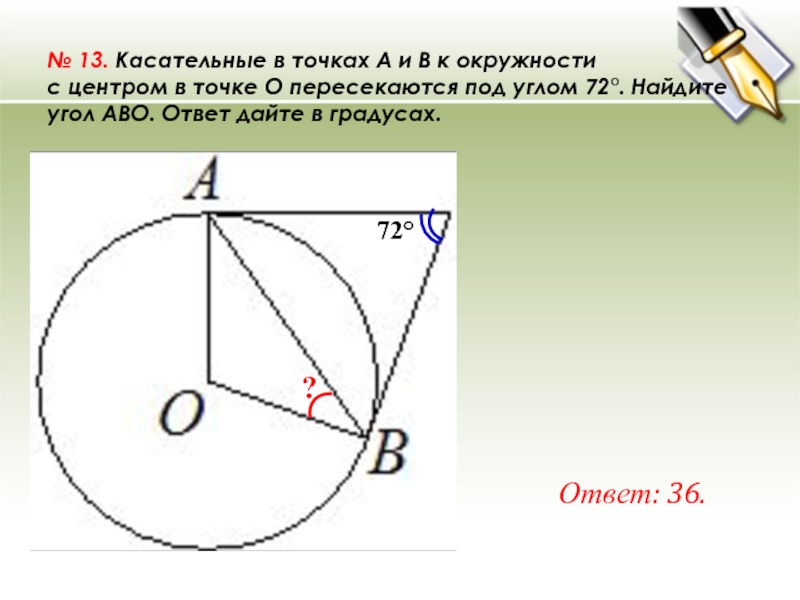
№ 13. Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах. Ответ: 36. 72° ?

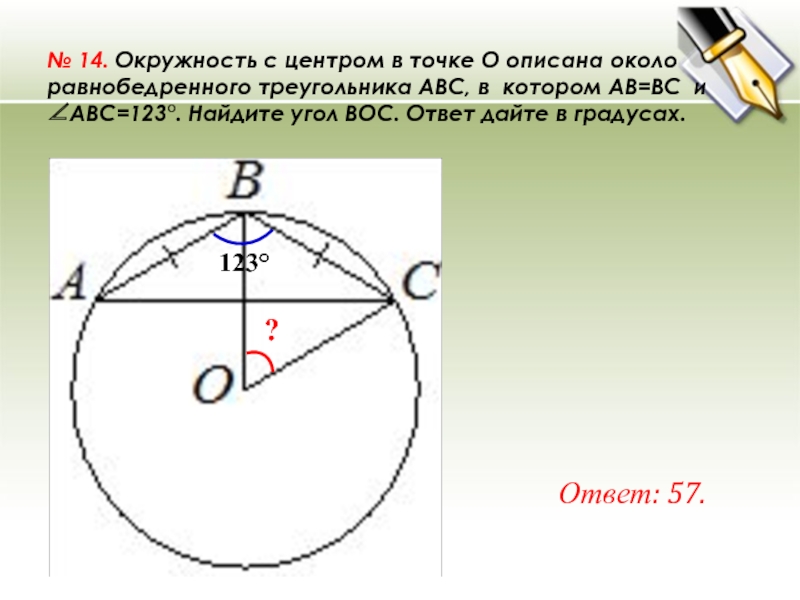
№ 14. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=123°. Найдите угол BOC. Ответ дайте в градусах. Ответ: 57. 123° ?

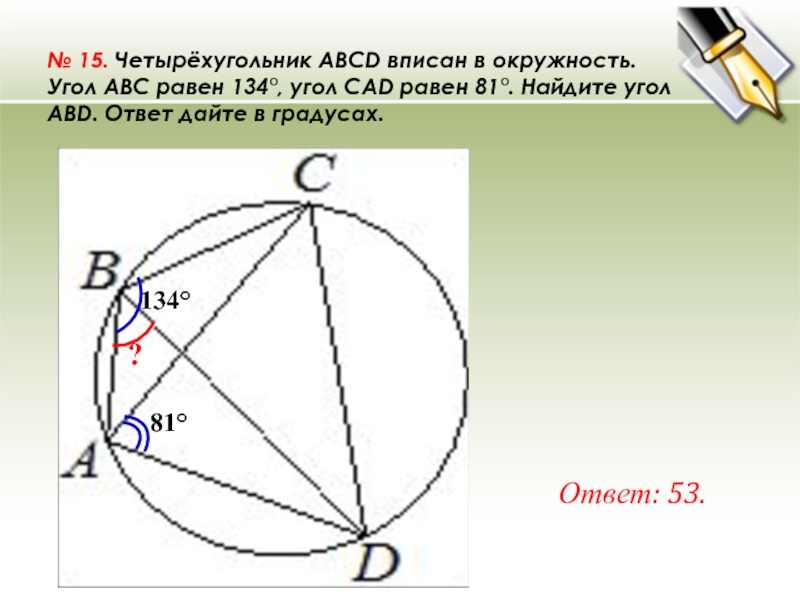
№ 15. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол ABD. Ответ дайте в градусах. Ответ: 53. 81° ? 134°

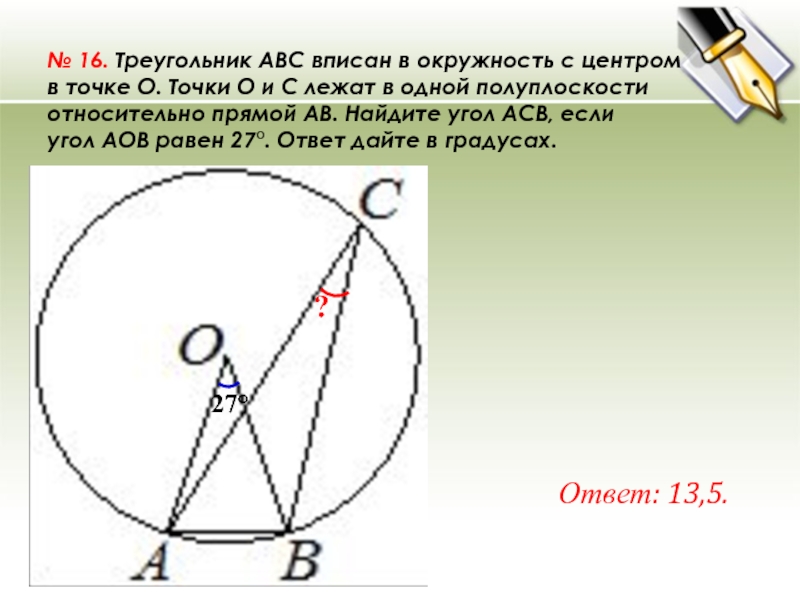
№ 16. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 27°. Ответ дайте в градусах. Ответ: 13,5. ? 27°

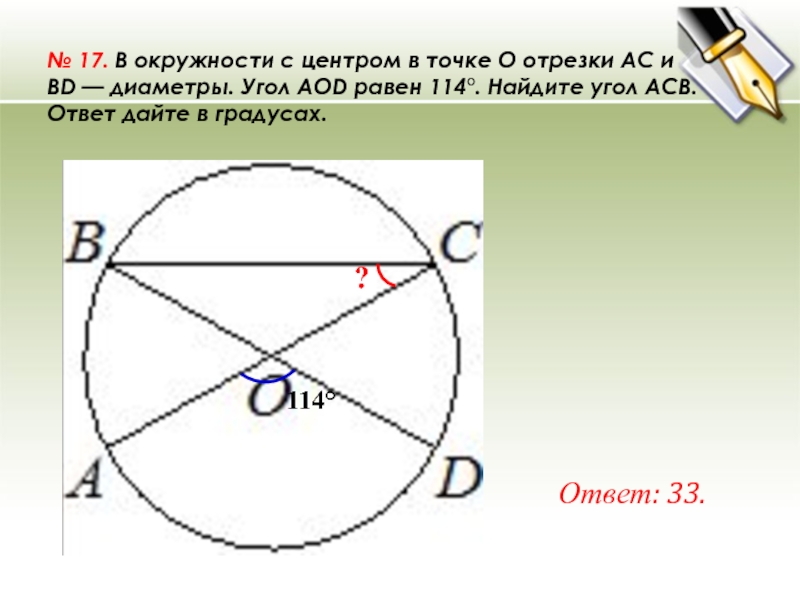
№ 17. В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах. Ответ: 33. ? 114°

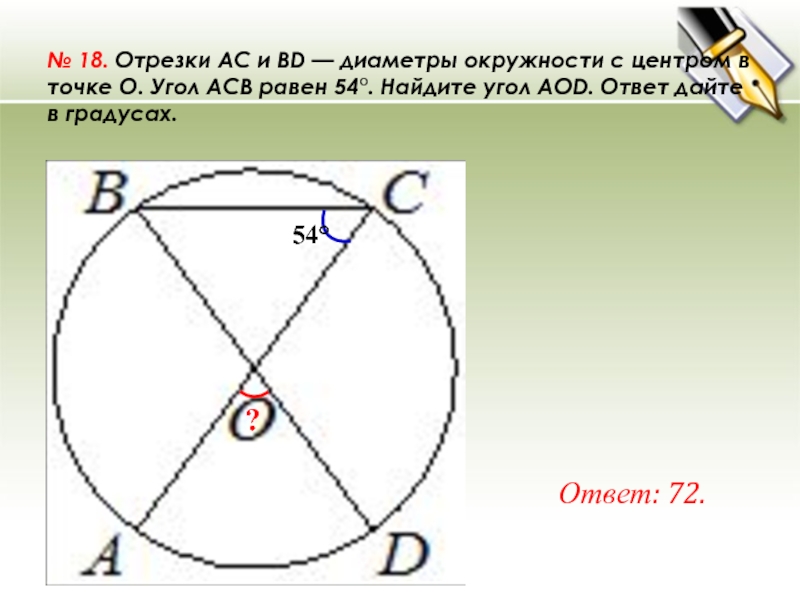
№ 18. Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах. Ответ: 72. ? 54°

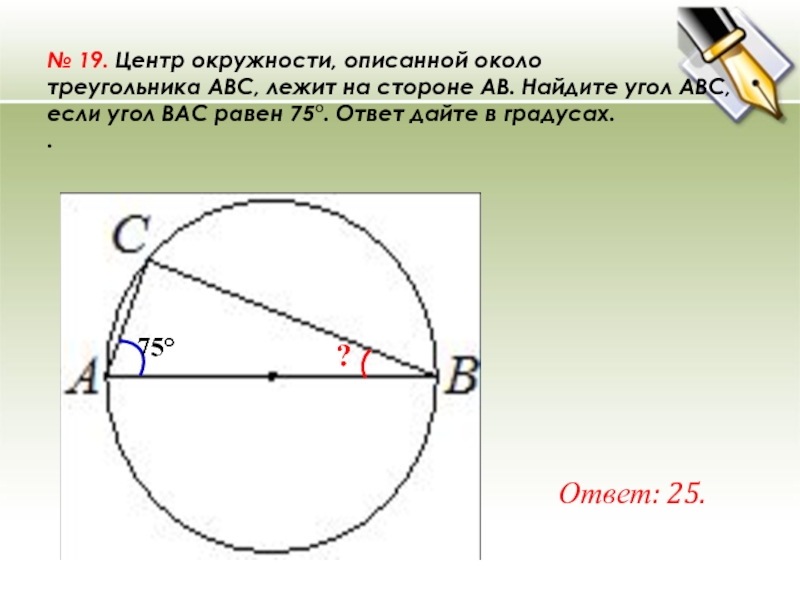
№ 19. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 75°. Ответ дайте в градусах. . Ответ: 25. ? 75°

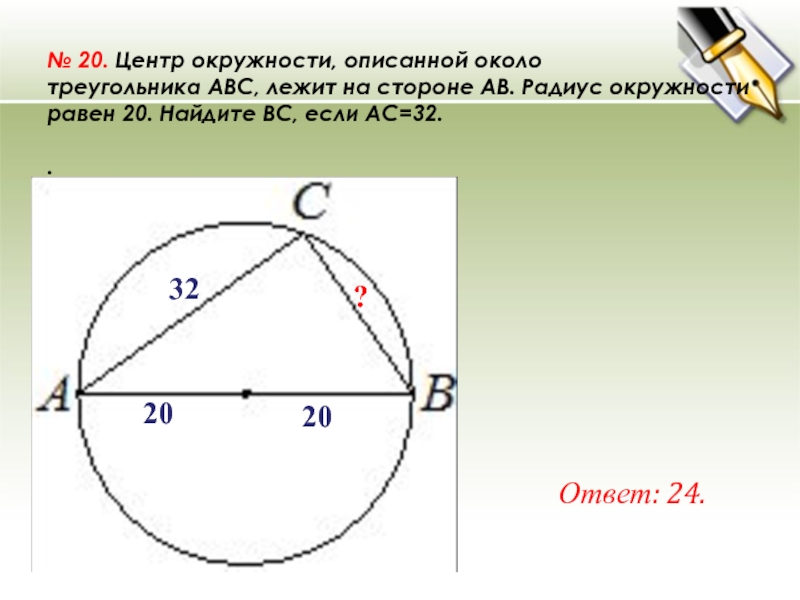
№ 20. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32. . Ответ: 24. ? 20 20 32

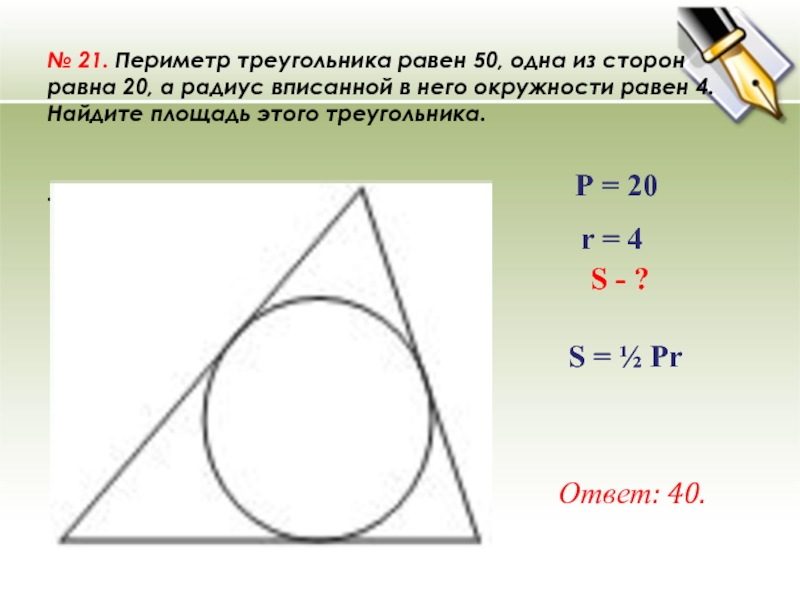
№ 21. Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника. . Ответ: 40. S — ? Р = 20 r = 4 S = ½ Pr

Видео:Как решать задания на окружность ОГЭ 2021? / Разбор всех видов окружностей на ОГЭ по математикеСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 943 человека из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 701 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 331 человек из 72 регионов

Ищем педагогов в команду «Инфоурок»

• Борисова Алла НиколаевнаНаписать 6782 21.05.2018

Номер материала: ДБ-1622909

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Утвержден список федеральных инновационных площадок в образовании на 2022 год

Время чтения: 1 минута

Стартовал региональный этап Всероссийской олимпиады школьников

Время чтения: 2 минуты

Более половины россиян сталкиваются с конфликтами в родительских чатах

Время чтения: 2 минуты

В Роспотребнадзоре заявили о широком распространении COVID-19 среди детей

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Проходной балл ЕГЭ для поступления на бюджет снизился впервые за 10 лет

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Видео:Вписанные и центральные углы #огэ #огэматематика #математикаСкачать

Презентация на тему Окружность (по материалам открытого банка задач ОГЭ по математике) 201 9

Презентация на тему Презентация на тему Окружность (по материалам открытого банка задач ОГЭ по математике) 201 9 из раздела Разное. Доклад-презентацию можно скачать по ссылке внизу страницы. Эта презентация для класса содержит 34 слайдов. Для просмотра воспользуйтесь удобным проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций TheSlide.ru в закладки!

Видео:Математика это не ИсламСкачать

Слайды и текст этой презентации

Окружность
(по материалам открытого банка задач ОГЭ по математике)

Подготовка к ОГЭ

Касательная к окружности
Прямая, имеющая с окружностью единственную общую точку, называется касательной к окружности.

Если прямая а, проходящая через точку на окружности, перпендикулярна радиусу, проведенному в эту точку, то прямая а-касательная к окружности.

Касательная перепндикулярна радиусу, проведенному в точку касания.

р – касательная к окружности с центром О
А – точка касания
OА — радиус

Свойство и признак касательной

Отрезки касательных к окружности, проведенные из одной точки равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Свойство отрезков касательных

Угол с вершиной в центре окружности называется центральным углом.

Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется вписанным углом.

Углы, связанные с окружностью

Величина дуги окружности равна величине центрального угла, на нее опирающегося.

Вписанный угол равен половине угловой величины дуги, на которую он опирается.

Углы, связанные с окружностью

Вписанные углы, опирающиеся на одну и ту же дугу, равны.

Вписанный угол, опирающийся на полуокружность – прямой.

Угол между касательной и хордой
равен половине угловой величины
дуги, заключенной между ними.

Теорема об отрезках пересекающихся хорд

Если две хорды окружности пересекаются, то
произведение отрезков одной хорды равно
произведению отрезков другой хорды.

Если из одной точки проведены к
окружности касательная и секущая,
то произведение всей секущей на
ее внешнюю часть равно квадрату
касательной.

Теорема о касательной и секущей

В любом вписанном четырёхугольнике сумма его противоположных углов равна 180°.

Обратная теорема. Если сумма противоположных улов четырехугольника равна 180 градусов, то около него можно описать окружность.

∠ A + ∠ C = ∠ B + ∠ D = 180°

Свойство вписанного четырёхугольника

В любом описанном четырёхугольнике суммы противоположных сторон равны.

Обратная теорема. Если суммы противоположных сторон выпуклого четырёхугольника равны, то в него можно вписать окружность.

Свойство описанного четырёхугольника

Какие из следующих утверждений верны?

1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.

2) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность не пересекаются.

3) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.

4) Около всякого треугольника можно описать не более одной окружности.

5) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.

Ответ: 1, 3, 4, 6, 8, 9 .

6) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.

7) Около любого ромба можно описать окружность.

8) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.

9) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.

№ 1. Радиус окружности, вписанной в трапецию, равен 42. Найдите высоту этой трапеции.

№ 2. Угол A четырёхугольника ABCD, вписанного в окружность, равен 37°. Найдите угол C этого четырёхугольника. Ответ дайте в градусах.

№ 3. На окружности отмечены точки A и B так, что меньшая дуга AB равна 92°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

№ 4. Через точку A, лежащую вне окружности, проведены
две прямые. Одна прямая касается окружности в точке K.
Другая прямая пересекает окружность в точках B и C, причём AB=4, AC=16. Найдите AK.

№ 5. Четырёхугольник ABCD описан около окружности, AB=7, BC=10, CD=14. Найдите AD.

№ 6. Хорды AC и BD окружности пересекаются в точке P, BP=15, CP=6, DP=10. Найдите AP.

№ 7. Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=8, DK=12, BC=6. Найдите AD.

№ 8. В треугольнике ABC угол C равен 120°, AB=18√3.
Найдите радиус окружности, описанной около этого треугольника.

№ 9. Четырёхугольник ABCD вписан в окружность. Угол ABD равен 39°, угол CAD равен 55°. Найдите угол ABC. Ответ дайте в градусах.

№ 10. В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B, точка O — центр окружности. Найдите угол AOB. Ответ дайте в градусах.

№ 11. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.

№ 12. Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=43°. Найдите угол BCO. Ответ дайте в градусах.

№ 13. Касательные в точках A и B к окружности с центром в точке O пересекаются под углом 72°. Найдите угол ABO. Ответ дайте в градусах.

№ 14. Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ABC=123°. Найдите угол BOC. Ответ дайте в градусах.

№ 15. Четырёхугольник ABCD вписан в окружность. Угол ABC равен 134°, угол CAD равен 81°. Найдите угол
ABD. Ответ дайте в градусах.

№ 16. Треугольник ABC вписан в окружность с центром в точке O. Точки O и C лежат в одной полуплоскости относительно прямой AB. Найдите угол ACB, если угол AOB равен 27°. Ответ дайте в градусах.

№ 17. В окружности с центром в точке O отрезки AC и
BD — диаметры. Угол AOD равен 114°. Найдите угол ACB. Ответ дайте в градусах.

№ 18. Отрезки AC и BD — диаметры окружности с центром в точке O. Угол ACB равен 54°. Найдите угол AOD. Ответ дайте в градусах.

№ 19. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 75°. Ответ дайте в градусах.
.

№ 20. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 20. Найдите BC, если AC=32.

№ 21. Периметр треугольника равен 50, одна из сторон равна 20, а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.

📽️ Видео

Шестнадцатое задание ОГЭ по математике (1) #огэ #огэ2023 #огэматематика #огэпоматематике #математикаСкачать

Удалили с экзамена ОГЭ Устное Собеседование shorts #shortsСкачать

ВПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

191 день до ОГЭСкачать

Функции за 15 секунд #семенкравченко #математика #огэ #умскул #shorts #клипыобразованиеСкачать

Урок 7. Окружность, круг и их элементы. ОГЭ. Вебинар |МатематикаСкачать

Графики функций за 10 секунд #огэ #математика #shortsСкачать

Фокус в математике #огэ #математика #shortsСкачать

Пятнадцатое задание ОГЭ по математике(12) #огэ #огэ2023 #огэпоматематике #математика #огэматематикаСкачать

Лайфхак при делении на 5 #огэ #огэматематика #математикаСкачать

Как строят линейную функцию в США #огэ #математика #shortsСкачать

ОГЭ №18 #огэ #математика #shortsСкачать