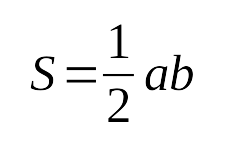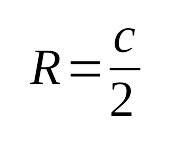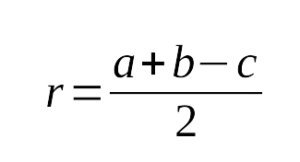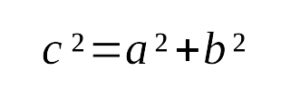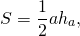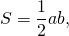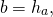Все признаки прямого треугольника

Видео:Свойства прямоугольного треугольника. 7 класс.Скачать

Определение

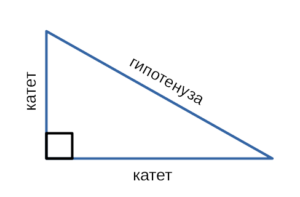
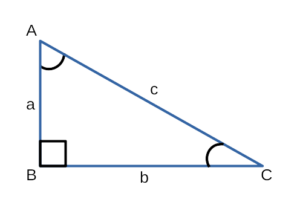
Прямоугольный треугольник — это треугольник, в котором один из углов прямой.

Гипотенуза в прямоугольном треугольнике — это сторона напротив прямого угла.

Катет в прямоугольном треугольнике — это две стороны прилежащие к прямому углу.

Видео:Геометрия 7. Урок 9 - Признаки равенства прямоугольных треугольниковСкачать

Свойства прямоугольного треугольника

В прямоугольном треугольнике:

1. Сумма острых углов 90˚.
2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. Медиана, проведенная к гипотенузе, равна ее половине.
4. Центр описанной окружности — середина гипотенузы.
   

Формулы:

1. Площадь прямоугольного треугольника равна
   половине произведения катетов:
   
2. Радиус описанной окружности около прямоугольного
   треугольника равен половине гипотенузы:
   
3. Радиус вписанной окружности в прямоугольный треугольник
   выражается следующим образом:
   
4. Квадрат гипотенузы равен сумме квадратов катетов:

Видео:7 класс, 36 урок, Признаки равенства прямоугольных треугольниковСкачать

Признаки равенства прямоугольных треугольников

С помощью признаков равенства прямоугольных треугольников
можно доказать что прямоугольные треугольники равны.

1. По двум катетам:
   Если два катета одного прямоугольного треугольника соответственно
   равны двум катетам другого прямоугольного треугольника,
   то такие треугольники равны.
   
2. По катету и гипотенузе:
   Если катет и гипотенуза одного прямоугольного треугольника соответственно
   равны катету и гипотенузе другого прямоугольного треугольника,
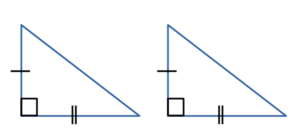
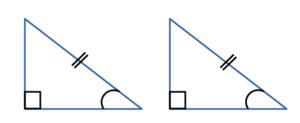
   то такие треугольники равны.
   
3. По гипотенузе и острому углу:
   Если гипотенуза и острый угол одного прямоугольного треугольника соответственно
   равны гипотенузе и острому углу другого прямоугольного треугольника,
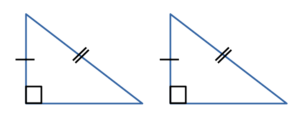
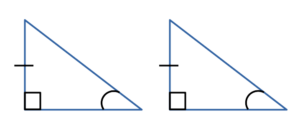
   то такие треугольникиравны.
   
4. По катету и острому углу:
   Если катет и острый угол одного прямоугольного треугольника соответственно
   равны катету и острому углу другого прямоугольного треугольника,
   то такие треугольники равны.

Видео:Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Признаки прямоугольного треугольника

С помощью признаков прямоугольного треугольника можно
доказать, что треугольник прямоугольный.

1. По теореме Пифагора:
   Если квадрат стороны равен сумме квадратов двух других сторон,
   то треугольник прямоугольный.
2. По центру описанной окружности:
   Если центр описанной окружности лежит на стороне треугольника,
   то треугольник прямоугольный.
3. По медиане:
   Если медиана треугольника равна половине стороны, к которой она проведена,
   то треугольник прямоугольный.
4. По площади:
   Если площадь треугольника равна половине произведения двух его сторон,
   то треугольник прямоугольный.
5. По радиусу описанной окружности:
   Если радиус описанной окружности равен половине,
   то треугольник прямоугольный.

Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Признаки подобия прямоугольных треугольников

С помощью признаков подобия прямоугольных треугольников можно
доказать, что прямоугольные треугольники подобны.

Видео:Признаки равенства треугольников. 7 класс.Скачать

Признаки прямоугольного треугольника

Самые известные признаки прямоугольного треугольника являются обратными теоремами к двум его свойствам.

Признаки прямоугольного треугольника.

Если квадрат стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник — прямоугольный.

2. Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник — прямоугольный.

3. Если центр описанной окружности лежит на стороне треугольника, то этот треугольник — прямоугольный.

Сторона, на которой лежит центр описанной около данного треугольника окружности, является гипотенузой.

4. Если радиус окружности, описанной около треугольника, равен половине его стороны, то этот треугольник прямоугольный.

(Если радиус равен половине стороны, то диаметр равен стороне. Значит, угол, лежащий напротив этой стороны — прямой (как вписанный угол, опирающийся на диаметр)).

Если на основании некоторых данных о треугольнике можно сделать вывод о том, что этот треугольник — прямоугольный, то соответствующее утверждение также может быть названо признаком прямоугольного треугольника.

Если площадь треугольника равна половине произведения двух его сторон, то этот треугольник — прямоугольный (а соответствующие стороны — его катеты).

Площадь треугольника можно найти по формуле

где a — стороны треугольника, h — высота, проведённая к стороне a. Если

то есть сторона b является высотой, проведённой к стороне a, а значит, стороны a и b перпендикулярны. Следовательно, такой треугольник — прямоугольный.

Видео:Все про прямоугольный треугольник. Решаем задачи | Математика | TutorOnlineСкачать

Прямоугольный треугольник

Прямоугольный треугольник – треугольник, в котором один угол прямой (то есть равен 90˚).

Сторона, противоположная прямому углу, называется гипотенузой прямоугольного треугольника.

Стороны, прилежащие к прямому углу, называются катетами .

Признаки равенства прямоугольных треугольников

Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны ( по двум катетам ).

Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны ( по катету и острому углу ).

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и острому углу ).

Если гипотенуза и катет одного прямоугольного треугольника равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны ( по гипотенузе и катету ).

Свойства прямоугольного треугольника

1. Сумма острых углов прямоугольного треугольника равна 90˚.

2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.

И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него лежит угол в 30˚.

3. Теорема Пифагора:

, где – катеты, – гипотенуза. Видеодоказательство

4. Площадь прямоугольного треугольника с катетами :

5. Высота прямоугольного треугольника, проведенная к гипотенузе выражается через катеты и гипотенузу следующим образом:

6. Центр описанной окружности – есть середина гипотенузы.

7. Радиус описанной окружности есть половина гипотенузы :

8. Медиана, проведенная к гипотенузе, равна ее половине

9. Радиус вписанной окружности выражается через катеты и гипотенузу следующим образом:

Тригонометрические соотношения в прямоугольном треугольнике смотрите здесь.

💥 Видео

Геометрия 7 класс (Урок№25 - Прямоугольные треугольники.)Скачать

Свойства прямоугольного треугольника. Практическая часть. 7 класс.Скачать

Геометрия 7 класс : Признаки равенства прямоугольных треугольниковСкачать

7 класс, 15 урок, Первый признак равенства треугольниковСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Решение прямоугольных треугольников. Практическая часть. 8 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

35. Некоторые свойства прямоугольных треугольниковСкачать

7 класс, 35 урок, Некоторые свойства прямоугольных треугольниковСкачать

7 кл г. Теорема: «катет лежавший напротив угла в 30 градусов равен половине гипотенузы»Скачать

7 класс. Признаки равенства прямоугольных треугольников.Скачать

Построение высоты в тупоугольном и прямоугольном треугольниках. 7 класс.Скачать

Нахождение стороны прямоугольного треугольникаСкачать