- Ваш ответ
- решение вопроса
- Похожие вопросы
- 10 Угольник вписанный в окружность
- Содержание
- Правильный десятиугольник [ править | править код ]
- Построение [ править | править код ]
- Разбиение правильного десятиугольника [ править | править код ]
- Пространственный десятиугольник [ править | править код ]
- Многоугольники Петри [ править | править код ]
- 🎬 Видео
Видео:Углы, вписанные в окружность. 9 класс.Скачать

Ваш ответ
Видео:Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

решение вопроса
Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

Похожие вопросы
- Все категории
- экономические 43,282
- гуманитарные 33,619
- юридические 17,900
- школьный раздел 607,036
- разное 16,829
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Построение девятиугольника циркулем, приближенноеСкачать

10 Угольник вписанный в окружность
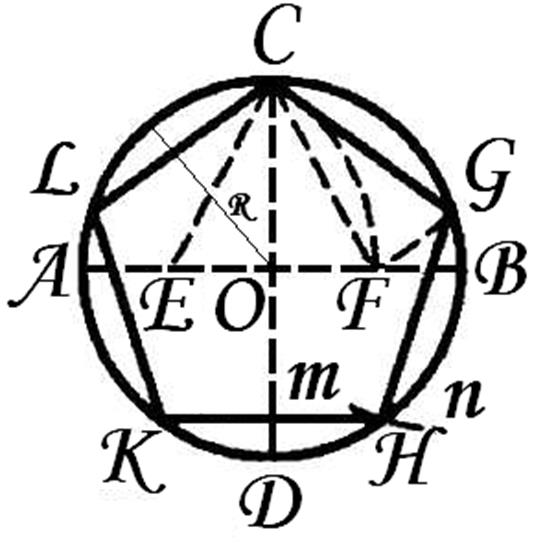
Десятиугольник, вписанный в окружность
Проводим два взаимно перпендикулярных диаметра АВ и CD. Делим пополам радиус АО в точке Е. Из Е радиусом ЕС проводим дугу CF, пересекая ею диаметр АВ в точке F. OF есть сторона искомой фигуры. С помощью циркуля, сделаем на окружности десять последовательных засечек. Получим вершины искомой фигуры. Подобно построению пятиугольника, вписанного в окружность.
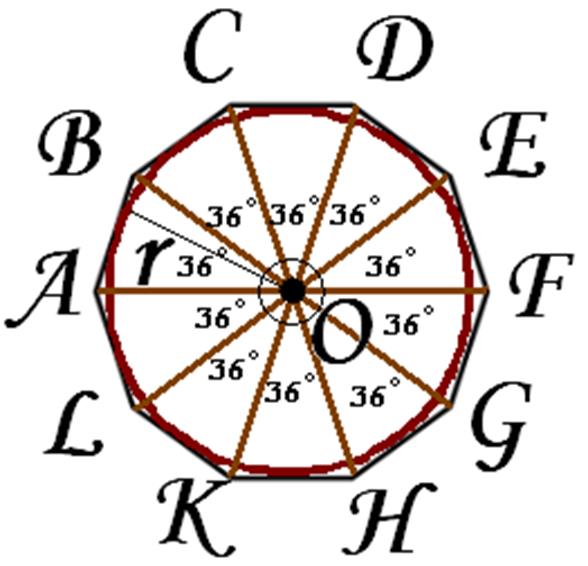
Десятиугольник, описанный около окружности
Имеем исходную окружность с центром в точке O. Так как сумма углов, составляющих центральный угол окружности, равна 360°. Делим данный угол на 10 частей (т.к. строим десятиугольник) с помощью транспортира, т.е. 360°:10=36°. Получаем 10 вершин: A, B, C, D, E, F, G, H, K, L. Соединяем эти вершины, получаем правильный десятиугольник.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Сдача сессии и защита диплома – страшная бессонница, которая потом кажется страшным сном. 8924 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
- Как начертить десятиугольник
- Как начертить угол без транспортира
- Как построить правильный восьмиугольник
- – циркуль;
- – линейка.
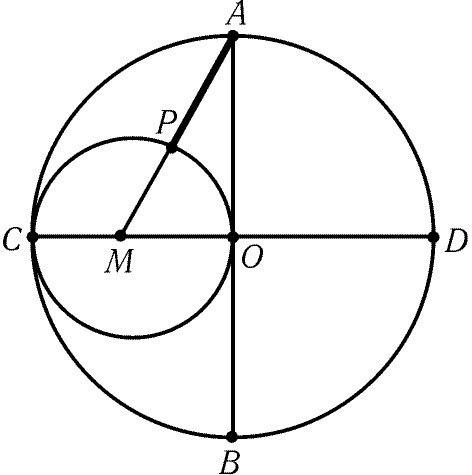
2 способ: Опять же, с помощью циркуля начертите окружность. Центр получившейся окружности обозначьте буквой О. Проведите два перпендикулярных диаметра данной окружности СD и АВ. Разделите один из 4-х радиусов на две равные части. Из рисунка видно, что радиус СО = СМ+МО, где СМ=МО.
Дальше поставьте ножку циркуля в точку М и начертите окружность радиусом, равным половине радиуса первоначальной окружности. С помощью линейки соедините центр маленькой окружности М с любой из 2-х точек (А или В) на перпендикулярном диаметре. На рисунке центр маленькой окружности соединен сточкой А. Длина, получившегося отрезка АМ будет равна длине стороны десятиугольника. Осталось только сделать раствор циркуля, равный длине отрезка АМ, поставить ножку циркуля в точку А и отметить следующую точку на окружности. Далее переместите ножку циркуля в новую точку и отметьте следующую. И так до тех пор, пока на окружности не появится 10 равноудаленных друг от друга точек.
| Правильный десятиугольник | |
|---|---|
 | |
| Сторон и вершин | 10 |
| Символ Шлефли | |
| Внутренний угол | 144° |
| Симметрия | Диэдрическая ( D 10 >  ), порядок 20. ), порядок 20. |
Десятиуго́льник (правильный десятиугольник — декагон) — многоугольник с десятью углами и десятью сторонами.
Видео:Задача 6 №27876 ЕГЭ по математике. Урок 117Скачать

Содержание
Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Правильный десятиугольник [ править | править код ]
У правильного десятиугольника все стороны равной длины, и каждый внутренний угол составляет 144°.
Площадь правильного десятиугольника равна (t — длина стороны):
A = 5 2 t 2 c t g π 10 = 5 t 2 2 5 + 2 5 ≈ 7.694 t 2 . >t^ ctg >= > > >>>approx 7.694t^ .>
Альтернативная формула A = 2.5 d t 
d = 2 t ( cos 3 π 10 + cos π 10 ) , >+cos >
ight),>
и может быть представлен в радикалах как
d = t 5 + 2 5 . >>>.>
Сторона правильного десятиугольника, вписанного в единичную окружность, равна 5 − 1 2 = 1 φ >-1> >= >> 

Радиус описанной окружности десятиугольника равен
R = 5 + 1 2 t , >+1> >t,>
а радиус вписанной окружности
r = 5 + 2 5 2 t . >>> >t.>
Построение [ править | править код ]
По теореме Гаусса — Ванцеля правильный десятиугольник возможно построить, используя лишь циркуль и линейку.
Иначе его можно построить следующим образом:
- Построить сначала правильный пятиугольник.
- Соединить все его вершины с центром описанной окружности прямыми до пересечения с этой же окружностью на противоположной стороне. В этих точках пересечения и находятся остальные пять вершин десятиугольника.
- Соединить по порядку вершины пятиугольника и пять точек, найденные шагом ранее. Искомый десятиугольник построен.
Видео:Геометрия 9 класс (Урок№21 - Правильный многоугольник. Описанная и вписанная окружность.)Скачать

Разбиение правильного десятиугольника [ править | править код ]
Гарольдом Коксетером было доказано, что правильный 2 m 


| Разбиение правильного десятиугольника |
|---|
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

Пространственный десятиугольник [ править | править код ]
| Правильные пространственные десятиугольники | ||
|---|---|---|
| # | # | # |
 | ||
Пентаграммная антипризма с перекрёстом
Пространственный десятиугольник — это пространственный многоугольник с десятью рёбрами и вершинами, но не лежащими в одной плоскости. У пространственного зиг-заг десятиугольника вершины чередуются между двумя параллельными плоскостями.
У правильного пространственного десятиугольника все рёбра равны. В трёхмерном пространстве это зиг-заг пространственный декагон, он может быть обнаружен среди рёбер и вершин пентагональной антипризмы, пентаграммной антипризмы, пентаграммной перекрещивающейся антипризмы с той же D5d [2 + ,10] симметрией порядка 20.
Его также можно найти в некоторых выпуклых многогранниках с икосаэдрической симметрией. Многоугольники по периметру этих проекций (см. ниже) это пространственные десятиугольники.
| Ортогональные проекции многогранников | |||
|---|---|---|---|
 Додекаэдр Додекаэдр | 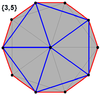 Икосаэдр Икосаэдр |  Икосододекаэдр Икосододекаэдр |  Ромботриаконтаэдр Ромботриаконтаэдр |
Многоугольники Петри [ править | править код ]
Правильный пространственный десятиугольник — это многоугольник Петри для многих многогранников высших размерностей, как показано на этих ортогональных проекциях на различных плоскостях Коксетера.
🎬 Видео
Вписанные и описанные окружности. Вебинар | МатематикаСкачать

9 класс, 22 урок, Окружность, описанная около правильного многоугольникаСкачать

9 класс, 23 урок, Окружность, вписанная в правильный многоугольникСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

ABCDEFGHI – правильный девятиугольник ... | ОГЭ 2017 | ЗАДАНИЕ 11 | ШКОЛА ПИФАГОРАСкачать

9 класс, 21 урок, Правильный многоугольникСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.Скачать

ЕГЭ База Задание 15 (Профиль Задание 6)Скачать

Четырёхугольник ABCD вписан в окружность ... | ОГЭ 2017 | ЗАДАНИЕ 10 | ШКОЛА ПИФАГОРАСкачать

Геометрия ОГЭ. Многоугольники #6 (задача 9 и 11 типа ФИПИ)🔴Скачать

Задача 6 №27916 ЕГЭ по математике. Урок 133Скачать