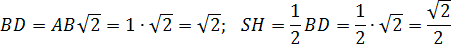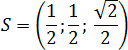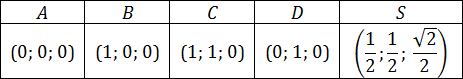Правильный четырехугольник пирамида sabcd (2 видео)

Правильный четырехугольник пирамида sabcd

SO – высота пирамиды, значит SO⊥OD и ΔSOD – прямоугольный.

Запишем для ΔSOD теорему Пифагора:

В основании правильной четырехугольной пирамиды лежит правильный четырехугольник, т.е. квадрат. Рассмотрим квадрат ABCD:

Содержание

Правильный четырехугольник пирамида sabcd
Вершины четырехугольной пирамиды
Что делать, когда ребра разные
Правильная четырехугольная пирамида
💡 Видео

Видео:Геометрия Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SBСкачать

Правильный четырехугольник пирамида sabcd

Решая задачу C2 методом координат, многие ученики сталкиваются с одной и той же проблемой. Они не могут рассчитать координаты точек, входящих в формулу скалярного произведения. Наибольшие трудности вызывают пирамиды. И если точки основания считаются более-менее нормально, то вершины — настоящий ад.

Сегодня мы займемся правильной четырехугольной пирамидой. Есть еще треугольная пирамида (она же — тетраэдр). Это более сложная конструкция, поэтому ей будет посвящен отдельный урок.

Для начала вспомним определение:

— это такая пирамида, у которой:

В основании лежит правильный многоугольник: треугольник, квадрат и т.д.;
Высота, проведенная к основанию, проходит через его центр.

В частности, основанием является квадрат. Прямо как у Хеопса, только чуть поменьше.

Ниже приведены расчеты для пирамиды, у которой все ребра равны 1. Если в вашей задаче это не так, выкладки не меняются — просто числа будут другими.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Вершины четырехугольной пирамиды

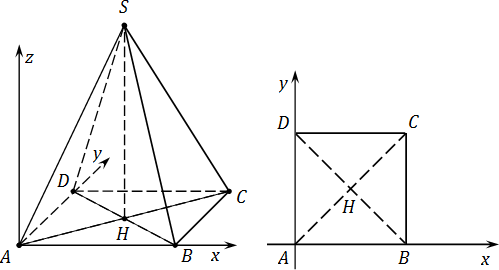
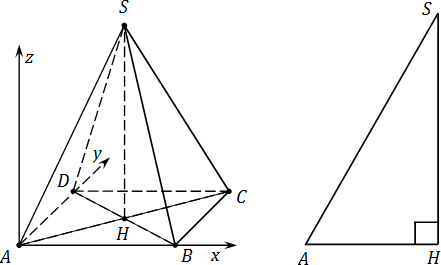
Итак, пусть дана правильная четырехугольная пирамида SABCD , где S — вершина, основание ABCD — квадрат. Все ребра равны 1. Требуется ввести систему координат и найти координаты всех точек. Имеем:

Вводим систему координат с началом в точке A :

Ось OX направлена параллельно ребру AB ;
Ось OY — параллельно AD . Поскольку ABCD — квадрат, AB ⊥ AD ;
Наконец, ось OZ направим вверх, перпендикулярно плоскости ABCD .

Теперь считаем координаты. Дополнительное построение: SH — высота, проведенная к основанию. Для удобства вынесем основание пирамиды на отдельный рисунок. Поскольку точки A , B , C и D лежат в плоскости OXY , их координата z = 0. Имеем:

A = (0; 0; 0) — совпадает с началом координат;
B = (1; 0; 0) — шаг на 1 по оси OX от начала координат;
C = (1; 1; 0) — шаг на 1 по оси OX и на 1 по оси OY ;
D = (0; 1; 0) — шаг только по оси OY .
H = (0,5; 0,5; 0) — центр квадрата, середина отрезка AC .

Осталось найти координаты точки S . Заметим, что координаты x и y точек S и H совпадают, поскольку они лежат на прямой, параллельной оси OZ . Осталось найти координату z для точки S .

Рассмотрим треугольники ASH и ABH :

AS = AB = 1 по условию;
Угол AHS = AHB = 90°, поскольку SH — высота, а AH ⊥ HB как диагонали квадрата;
Сторона AH — общая.

Следовательно, прямоугольные треугольники ASH и ABH равны по одному катету и гипотенузе. Значит, SH = BH = 0,5 · BD . Но BD — диагональ квадрата со стороной 1. Поэтому имеем:

Итого координаты точки S :

В заключение, выпишем координаты всех вершин правильной прямоугольной пирамиды:

Видео:10 кл.Егэ. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S верСкачать

Что делать, когда ребра разные

А что, если боковые ребра пирамиды не равны ребрам основания? В этом случае рассмотрим треугольник AHS :

Треугольник AHS — прямоугольный, причем гипотенуза AS — это одновременно и боковое ребро исходной пирамиды SABCD . Катет AH легко считается: AH = 0,5 · AC . Оставшийся катет SH найдем по теореме Пифагора. Это и будет координата z для точки S .

Видео:Задача про четырёхугольную пирамидуСкачать

Правильная четырехугольная пирамида

Продолжаем рассматривать задачи входящие в ЕГЭ по математике. Мы уже исследовали задачи, где в условии дан составной многогранник и требуется найти расстояние между двумя данными точками либо угол.

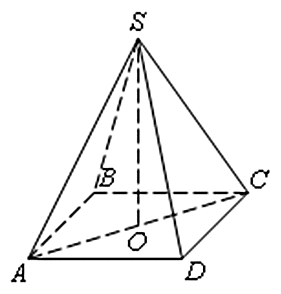
Пирамида — это многогранник, основание которого является многоугольником, остальные грани — треугольники, при чём они имеют общую вершину.

Правильная пирамида — это пирамида в основании которой лежит правильный многоугольник, а его вершина проецируется в центр основания.

Правильная четырехугольная пирамида — снованием является квадрат.Вершина пирамиды проектируется в точку пересечения диагоналей основания (квадрата).

ML — апофема
∠MLO — двугранный угол при основании пирамиды
∠MCO — угол между боковым ребром и плоскостью основания пирамиды

В этой статье мы с вами рассмотрим задачи на решение правильной пирамиды. Требуется найти какой-либо элемент, площадь боковой поверхности, объём, высоту. Разумеется, необходимо знать теорему Пифагора, формулу площади боковой поверхности пирамиды, формулу для нахождения объёма пирамиды.

В статье « Общий обзор. Формулы стереометрии! » представлены формулы, которые необходимы для решения задач по стереометрии. Итак, задачи:

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 51, AC = 136. Найдите боковое ребро SC .

В данном случае в основании лежит квадрат. Это означает, что диагонали AC и BD равны, они пересекаются и точкой пересечения делятся пополам. Отметим, что в правильной пирамиде высота опущенная из её вершины проходит через центр основания пирамиды. Таким образом, SO является высотой, а треугольник SOC прямоугольный. Тогда по теореме Пифагора:

Как извлекать корень из большого числа описано здесь .

Решите самостоятельно:

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SC = 5, AC = 6. Найдите длину отрезка SO.

В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, SC = 5. Найдите длину отрезка AC.

В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 7, а SR = 16. Найдите площадь боковой поверхности.

Площадь боковой поверхности правильной треугольной пирамиды равна половине произведения периметра основания на апофему (апофема это высота боковой грани правильной пирамиды, проведённая из её вершины):

Или можно сказать так: площадь боковой поверхности пирамиды равна сумме площадей трёх боковых граней. Боковыми гранями в правильной треугольной пирамиде являются равные по площади треугольники. В данном случае:

Решите самостоятельно:

В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SR.

В правильной треугольной пирамиде SABC L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 25, объем пирамиды равен 100. Найдите длину отрезка MS.

Основание пирамиды — равносторонний треугольник . Поэтому M является центром основания, а MS — высотой правильной пирамиды SABC . Объем пирамиды SABC равен:

Решите самостоятельно:

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Объем пирамиды равен 1, MS = 1. Найдите площадь треугольника ABC.

На этом закончим. Как видите, задачи решаются в одно-два действия. В будущем рассмотрим с вами другие задачи из данной части, где даны тела вращения, не пропустите!