Правильная пирамида в основании четырехугольник (8 видео)

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Когда человек слышит слово «пирамида», то сразу вспоминает величественные египетские сооружения. Тем не менее древние каменные гиганты являются лишь одним из представителей класса пирамид. В данной статье рассмотрим с геометрической точки зрения свойства правильной четырехугольной пирамиды .

Содержание

Что такое пирамида в общем случае?
Правильная четырехугольная пирамида
Четыре основных линейных параметра
Площадь и объем фигуры
Свойства правильной усеченной четырехугольной пирамиды
Что такое правильная пирамида: определение, виды, свойства
Определение правильной пирамиды
Виды правильной пирамиды
Правильная треугольная пирамида
Правильная четырехугольная пирамида
Правильная шестиугольная пирамида
Свойства правильной пирамиды
Правильная четырехугольная пирамида
В основании пирамиды правильный четырехугольник — квадрат (все стороны которого равны, углы между сторонами основания составляют 90 градусов).
Популярное
📸 Видео

Видео:Найти площадь поверхности правильной четырехугольной пирамидыСкачать

Что такое пирамида в общем случае?

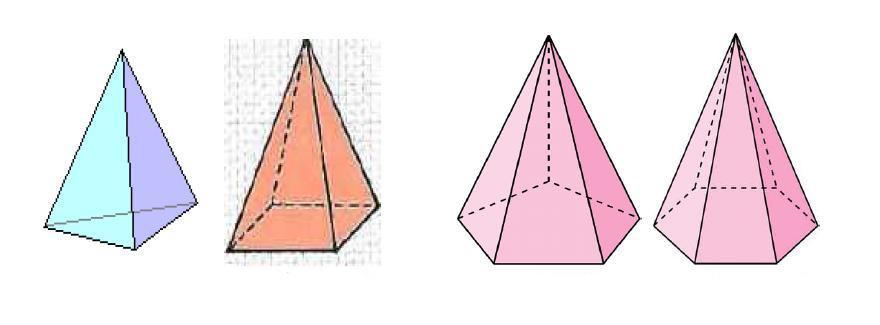
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

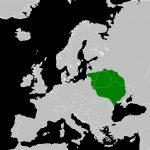
Мы видим что первая фигура имеет треугольное основание, вторая — четырехугольное. Две последние представлены пяти- и шестиугольным основанием. Однако боковая поверхность всех пирамид образована треугольниками. Их число точно равно количеству сторон или вершин многоугольника в основании.

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

в основании должен находиться правильный многоугольник;
боковая поверхность фигуры должна состоять из равных равнобедренных треугольников.

Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Видео:КАК НАЙТИ ПЛОЩАДЬ БОКОВОЙ ПОВЕРХНОСТИ ПИРАМИДЫ?Скачать

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Видео:10 класс, 33 урок, Правильная пирамидаСкачать

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Видео:Построение сечения пирамиды по трем точкамСкачать

Площадь и объем фигуры

Это еще два важных свойства правильной четырехугольной пирамиды . Основание фигуры имеет следующую площадь:

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

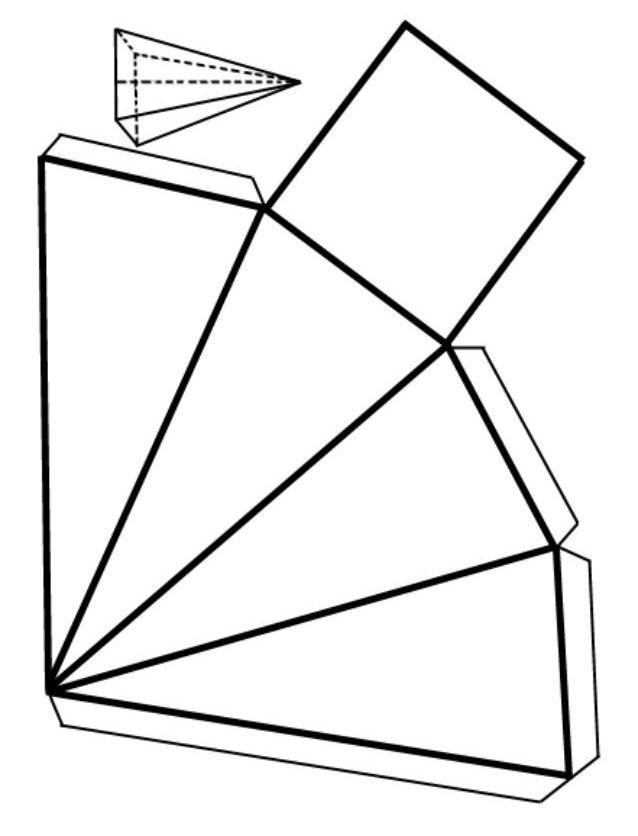
Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Видео:№259. В правильной четырехугольной пирамиде сторона основания равна 6 см, а угол наклона боковойСкачать

Свойства правильной усеченной четырехугольной пирамиды

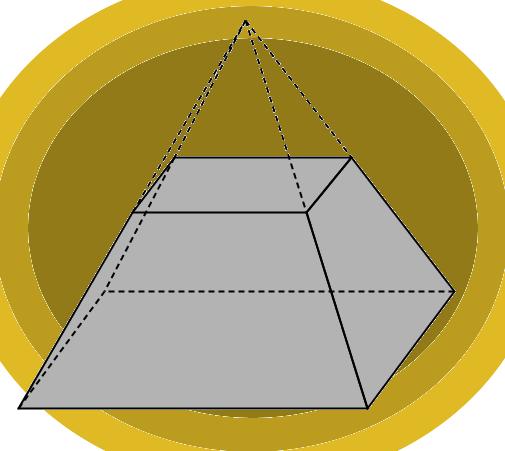
Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Удобнее всего изучать характеристики усеченной пирамиды, если ее основания параллельны друг другу. В этом случае нижнее и верхнее основания будут подобными многоугольниками. Поскольку в четырехугольной правильной пирамиде основание — это квадрат, то образованное при срезе сечение тоже будет представлять квадрат, но уже меньшего размера.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Здесь h — расстояние между основаниями фигуры, So1, So2 — площади нижнего и верхнего оснований.

Видео:Правильная пирамида № 258Скачать

Что такое правильная пирамида: определение, виды, свойства

В данной публикации мы рассмотрим определение, виды (треугольная, четырехугольная, шестиугольная) и основные свойства правильной пирамиды. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Видео:Пирамида. 11 класс.Скачать

Определение правильной пирамиды

Правильная пирамида – это пирамида, основанием которой является правильный многоугольник, а вершина фигуры проецируется в центр ее основания.

Самые распространенные разновидности правильных пирамид: треугольная, четырехугольная и шестиугольная. Рассмотрим их подробнее.

Видео:10 класс, 32 урок, ПирамидаСкачать

Виды правильной пирамиды

Правильная треугольная пирамида

Основание – правильный/равносторонний треугольник ABC.
Боковые грани – одинаковые равнобедренные треугольники: ADC, BDC и ADB.

Примечание: если у правильной треугольной пирамиды все ребра равны, она также называется правильным тетраэдром.

Правильная четырехугольная пирамида

Основание – правильный четырехугольник ABCD, другими словами, квадрат.
Боковые грани – равные равнобедренные треугольники: AEB, BEC, CED и AED.
Проекция вершины E на основание – точка O, является точкой пересечения диагоналей квадрата ABCD.
EO – высота фигуры.
EN и EM – апофемы (всего их 4, на рисунке в качестве примера изображено только два).

Правильная шестиугольная пирамида

Основание – правильный шестиугольник ABCDEF.
Боковые грани – равные равнобедренные треугольники: AGB, BGC, CGD, DGE, EGF и FGA.
Проекция вершины G на основание – точка O, является точкой пересечения диагоналей/биссектрис шестиугольника ABCDEF.
GO – высота пирамиды.
GN – апофема (всего их должно быть шесть).

Видео:Найдите отрезок АС в правильной четырехугольной пирамидеСкачать

Свойства правильной пирамиды

Все боковые ребра фигуры равны. Другими словами вершина пирамиды находится на одинаковом расстоянии от всех углов ее основания.
Угол между всеми боковыми ребрами и основанием одинаковый.
Все грани наклонены к основанию под одним и тем же углом.
Площади всех боковых граней равны.
Все апофемы равны.
Вокруг пирамиды можно описать сферу, центром которой будет точка пересечения перпендикуляров, проведенных к серединам боковых ребер.