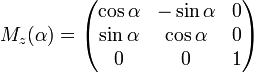Поворот вектора вокруг z

В данной статье на конкретном примере рассматриваются особенности применения различных методов поворота 3D объекта в пространстве. В частности, сравнивается применение углов Эйлера и кватернионов.

Данная статья пригодится вам, если вы уже прочитали определение кватерниона и давно ищете наглядный материал для того, чтобы понять, зачем придумали кватернионы, и чем же они отличаются от углов Эйлера.

Наглядная демонстрация поворота по углам Эйлера уже была описана в статье на Хабре, особенно интересно поиграть с моделью самолётика (ссылки на программу в той же статье внизу).

Заручившись помощью чудесного сайта tinkercad.com представляю вам более наглядную демонстрацию поворотов предмета по углам Эйлера и сравнение с поворотом на основе кватерниона.

Видео:Матрица поворотаСкачать

Демонстрация поворотов по углам Эйлера

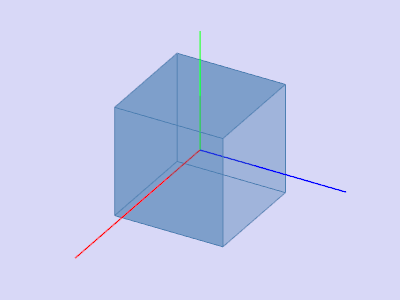
Поворачивать будем избушку на курьих ножках. Вот ссылка на модель: Izba3D.

Рис. 1. Избушка в изометрии

Поворот вокруг оси Z, а потом оси Y

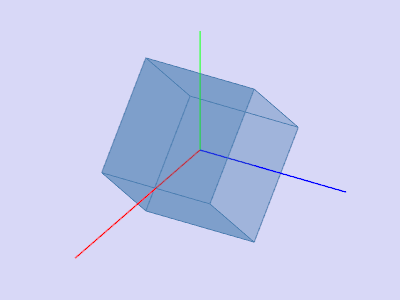
Рис. 2. Результат поворота рисунка 1 на 90 градусов вокруг оси Z

1. Повернуть на 90 градусов вокруг оси Y

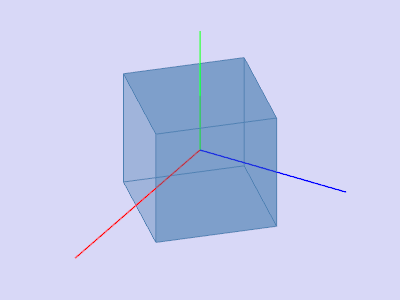
Рис. 3. Результат поворота рисунка 2 на 90 градусов вокруг оси Y

Поворот вокруг оси Y, а потом оси Z

Рис. 4. Результат поворота рисунка 1 на 90 градусов вокруг оси Y

1. Повернуть на 90 градусов вокруг оси Z

Рис. 5. Результат поворота рисунка 4 на 90 градусов вокруг оси Z

Сравнение и выводы

Сравним получившиеся картинки:

Рис. 6. Сравнение результатов поворота

Вывод: Порядок применения поворотов влияет на результат.

Видео:А.7.19 Поворот в трехмерном пространствеСкачать

Кватернион

Гораздо удобнее пользоваться кватернионом, а именно, вектором и величиной поворота вокруг этого вектора.

Допустим, мы хотим повернуть избушку вокруг зелёного крылечка на 90, а потом снова на 90 градусов. Тогда пусть направление вектора совпадает с направлением зелёного крылечка.

Рис. 7. Избушка на курьих ножках с зелёным крылечком

Рис. 8. Поворот на 90 градусов вокруг вектора, совпадающего с крылечком

Рис. 9. Второй поворот на 90 градусов вокруг вектора, совпадающего с крылечком

Видео:Часть 3 Поворот вектораСкачать

Вращение фигуры в 3-х мерном пространстве

Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.

Матрица поворота в трёхмерном пространстве

Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x: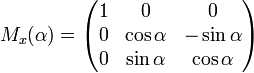

Вращение вокруг оси y: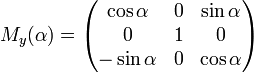

Вращение вокруг оси z:

После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;

По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);

По оси Z
x’=x*cos(L)-y*sin(L);
y’=-x*sin(L)+y*cos(L);
z’=z;

Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.

Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).

Видео:Алгебра 10 класс Поворот точки вокруг начала координат ЛекцияСкачать

Матрицы поворота, углы Эйлера и кватернионы (Rotation matrices, Euler angles and quaternions)

Объект обычно определяется в удобной для его описания локальной системе координат (ЛСК), а его положение в пространстве — в глобальной системе координат (ГСК).

В трёхмерном пространстве переход из одной СК в другую описывается в общем случае системой линейных уравнений:

Уравнения могут быть записаны через матрицы аффинных преобразований в однородных координатах одним из 2-х способов:

В ортогональных СК оси X, Y и Z взаимно перпендикулярны и расположены по правилу правой руки:

На рисунке справа большой палец определяет направление оси, остальные пальцы — положительное направление вращения относительно этой оси.

Все три вектора направлений есть единичными.

Ниже приводится единичная матрица для 2-х способов записи уравнений геометрических преобразований. Такая матрица не описывает ни перемещения, ни вращения. Оси ЛСК и ГСК совпадают.

Далее рассматривается матрица для второго способа матричной записи уравнений (матрица справа). Этот способ встречается в статьях значительно чаще.

При использовании матрицы вы можете игнорировать нижнюю строку. В ней всегда хранятся одни и те же значения 0, 0, 0, 1. Она добавлена для того, чтобы мы могли перемножать матрицы (напомню правило перемножения матриц и отмечу, что всегда можно перемножать квадратные матрицы). Подробнее см. Композиция матриц. Однородные координаты.

Остальные 12 значений определяют координатную систему. Первый столбец описывает компоненты направления оси X(1,0,0). Второй столбец задает направление оси Y(0,1,0), третий – оси Z (0,0,1). Последний столбец определяет положение начала системы координат (0,0,0).

Как будет выглядеть матрица Евклидового преобразования (преобразование движения) для задания ЛСК , с началом в точке (10,5,0) и повёрнутой на 45° вокруг оси Z глобальной СК, показано на рисунке.

Рассмотрим сначала ось X. Если новая система координат повернута на 45° вокруг оси z, значит и ось x повернута относительно базовой оси X на 45° в положительном направлении отсчета углов. Таким образом, ось X направлена вдоль вектора (1, 1, 0), но поскольку вектор системы координат должен быть единичным, то результат должен выглядеть так (0.707, 0.707, 0). Соответственно, ось Y имеет отрицательную компоненту по X и положительную по Y и будет выглядеть следующим образом (-0.707, 0.707, 0). Ось Z направления не меняет (0, 0, 1). Наконец, в четвертом столбце вписываются координаты точки начала системы координат (10, 5, 0).

Частным случаем матриц геометрических преобразований есть матрицы поворота ЛСК относительно базовых осей ГСК. Вектора осей ЛСК здесь выражены через синусы и косинусы углов вращения относительно оси, перпендикулярной к плоскости вращения.

От матрицы преобразований размером 4*4 можно перейти непосредственно к матрице поворота 3*3, убрав нижний ряд и правый столбец. При этом, система линейных уравнений записывается без свободных элементов (лямда, мю, ню), которые определяют перемещение вдоль осей координат.

Путем перемножения базовых матриц можно получать комбинированные вращения. Ниже рассмотрены возможности комбинировать вращениями через матрицы поворота на примерах работы с углами Эйлера.

Видео:Матрицы масштабирования, переноса и поворотаСкачать

Матрицы поворота и углы Эйлера

От выбора осей и последовательности вращения зависит конечный результат. На рисунках отображена следующая последовательность вращения относительно осей ЛСК:

• оси Z (угол alpha);
• оси X (угол beta);
• оси Z (угол gamma).

Получил от читателя этой статьи вопрос: «Как понять, из каких углов поворота вокруг осей X,Y,Z можно получить текущее положение объекта, когда в качестве задания мы уже имеем повернутый объект, а нужно вывести его в это положение, последовательно повернув его из какого-то начального положения до полного совмещения с заданным?»

Мой ответ: «Если я правильно понял вопрос, то Вас интересует, как от начального положения перейти к заданному положению объекта, используя для этого элементарные базовые аффинные преобразования.

Начну с аналогии. Это как в шахматах. Мы знаем как ходит конь. Необходимо переместить его в результате многоходовки в нужную клетку на доске — при условии, что это возможно.

Подробно эта проблематика рассмотрена в статье Преобразование координат при калибровке роботов.

Умение правильно выбирать последовательность элементарных геометрических преобразований помогает в решении множества других задач (см. Примеры геометрических преобразований).»

Можно получить результирующую матрицу, которая определяет положение ГСК относительно ЛСК. Для этого необходимо перемножить матрицы с отрицательными углами в последовательности выполнения поворотов:

Почему знак угла поворота меняется на противоположный? Объяснение этому простое. Движение относительно. Абстрагируемся и представим, что ГСК меняет положение относительно неподвижной ЛСК. При этом направление вращения меняется на противоположное.

Перемножение матриц даст следующий результат:

Результирующую матрицу можно использовать для пересчета координат из ГСК в ЛСК:

Для пересчета координат из ЛСК в ГСК используется результирующая обратная матрица.

В обратной матрице последовательность поворота и знаки углов меняются на противоположные (в рассматриваемом примере снова на положительные) по сравнению с матрицей определения положения ГСК относительно ЛСК.

Перемножение матриц даст следующий результат:

Выше был рассмотрен случай определения углов Эйлера через вращение относительно осей ЛСК. То же взаимное положение СК можно получить, выполняя вращение относительно осей ГСК:

• оси z (угол (gamma+pi/2));
• оси y (угол угол beta);
• оси z (угол (-alpha)).

Определение углов Эйлера через вращение относительно осей ГСК позволяет также просто получить зависимости для пересчета координат из ЛСК в ГСК через перемножение матриц поворота.

В рамках рассматриваемой задачи вместо угла gamma в матрицe Az используем угол gamma+pi/2.

Также легко можно перейти к зависимостям для пересчета координат из ГСК в ЛСК.

Обратная матрица получается перемножением обратных матриц в обратном порядке по сравнению с прямым преобразованием. При этом каждая из обратных матриц вращения может быть получена заменой знака угла на противоположный.

Детально с теоретическими основами аффинных преобразований (включая и вращение) можно ознакомиться в статье Геометрические преобразования в графических приложениях

Примеры преобразований рассмотрены в статьях:

Видео:ИМРС 5.2 Матрица поворотаСкачать

Axis Angle представление вращения

Выбрав подходящую ось (англ. rotation axis) и угол (англ. rotation angle) можно задать любую ориентацию объекта.

Обычно хранят ось вращения в виде единичного вектора и угол поворота вокруг этой оси в радианах или градусах.

q = [ x, y, z, w ] = [ v, w ]

В некоторых случаях удобно хранить угол вращения и ось в одном векторе. Направление вектора при этом совпадает с направлением оси вращения, а его длина равна углу поворота:

q = [ x, y, z]; w=sqrt (x*x +y*y +z*z)

В физике, таким образом хранят угловую скорость. Направление вектора совпадает с направлением оси вращения, а длина вектора равна скорости (в радианах в секунду).

Можно описать рассмотренные выше углы Эйлера через Axis Angle представление в 3 этапа:

q1 = [ 0, 0, 1, alpha]; q2 = [ 1, 0, 0, beta]; q3 = [ 0, 0, 1, gamma ]

Здесь каждое вращение выполняется относительно осей текущего положения ЛСК. Такое преобразование равнозначно рассмотренному выше преобразованию через матрицы поворота:

Возникает вопрос, а можно ли 3 этапа Axis Angle представления объединить в одно, подобно матрицам поворота? Попробуем решить геометрическую задачу по определению координат последнего вектора вращения в последовательности преобразований через Axis Angle представления:

q = [ x, y, z, gamma ]

Есть ли представление q= [x, y, z, gamma] композицией последовательности из 3-х этапов преобразований? Нет! Координаты x, y, z определяют всего лишь положение оси Z ЛСК после первого и второго этапов преобразований:

При этом ось Z, отнюдь, не есть вектор вращения для Axis Angle представления, которое могло бы заменить рассмотренные 3-х этапа преобразований.

Еще раз сформулирую задачу, которая математически пока не решена: «Необходимо найти значение угла (rotation angle) и положение оси (rotation axis), вращением относительно которой на этот угол можно заменить комбинацию из 3-х поворотов Эйлера вокруг осей координат».

К сожалению, никакие операции (типа объединения нескольких преобразований в одно) с Axis Angle представлениями нельзя выполнить. Не будем расстраиваться. Это можно сделать через кватернионы, которые также определяют вращение через параметры оси и угол.

Видео:§35 Формулы поворота координатных осейСкачать

Кватернионы

Кватернион (как это и видно по названию) представляет собой набор из четырёх параметров, которые определяют вектор и угол вращения вокруг этого вектора. По сути такое определение ничем не отличается от Axis Angle представления вращения. Отличия лишь в способе представления. Как же хранят вращение в кватернионе?

q = [ V*sin(alpha/2), cos(alpha/2) ]

В кватернионе параметры единичного вектора умножается на синус половины угла поворота. Четвертый компонент — косинус половины угла поворота.

Таблица с примерами значений кватернионов:

Представление вращения кватернионом кажется необычным по сравнению с Axis Angle представлением. Почему параметры вектора умножаются на синус половины угла вращения, четвертый параметр — косинус половины угла вращения, а не просто угол?

Откуда получено такое необычное представление кватерниона детально можно ознакомиться в статье Доступно о кватернионах и их преимуществах. Хотя программисту не обязательно знать эти детали, точно также как и знать, каким образом получены матрицы преобразования пространства. Достаточно лишь знать основные операции с кватернионами, их смысл и правила применения.

Видео:А.7.18 Вот: это поворот!!! (+ДЗ)Скачать

Основные операции над кватернионами

Кватернион удобно рассматривать как 4d вектор, и некоторые операции с ним выполняются как над векторами.

Видео:A.7.19+ Осторожно! Нюанс с поворотом вокруг Y!Скачать

Сложение, вычитание и умножение на скаляр.

Смысл операции сложения можно описать как «смесь» вращений, т.е. мы получим вращение, которое находится между q и q’.

Что-то подобное сложению кватернионов выполнялось при неудачной попытке объединить 3 этапа Axis Angle представления.

Умножение на скаляр на вращении не отражается. Кватернион, умноженный на скаляр, представляет то же самое вращение, кроме случая умножения на 0. При умножении на 0 мы получим «неопределенное» вращение.

Пример сложения 2-х кватернионов:

Видео:Бесконечно малый поворотСкачать

Норма и модуль

Следует различать (а путают их часто) эти две операции:

Модуль (magnitude), или как иногда говорят «длина» кватерниона:

Через модуль кватернион можно нормализовать. Нормализация кватерниона — это приведение к длине = 1 (так же как и в векторах):

Видео:Формула поворота РодригаСкачать

Обратный кватернион или сопряжение ( conjugate )

Обратный кватернион задает вращение, обратное данному. Чтобы получить обратный кватернион достаточно развернуть вектор оси в другую сторону и при необходимости нормализовать кватернион.

Например, если разворот вокруг оси Y на 90 градусов = (w=0,707; x = 0; y = 0,707; z=0), то обратный = (w=0,707; x = 0; y = -0,707; z=0).

Казалось бы, можно инвертировать только компоненту W, но при поворотах на 180 кватернион представляется как (w=1; x = 0; y = 0; z=0), то есть, у него длина вектора оси = 0.

Фрагмент программной реализации:

Видео:Дынников И.А.- Аналитическая геометрия - 6.Поворот вокруг вектора в пространстве. Двойственный базисСкачать

Инверсный (inverse) кватернион

Существует такой кватернион, при умножении на который произведение дает нулевое вращение и соответствующее тождественному кватерниону (identity quaternion), и определяется как:

Видео:A.7.28 Описание поворотов кватернионамиСкачать

Тождественный кватернион

Записывается как q[0, 0, 0, 1]. Он описывает нулевой поворот (по аналогии с единичной матрицей), и не изменяет другой кватернион при умножении.

Видео:Трехмерные линейные трансформации | Сущность Линейной Алгебры, примечаниеСкачать

Скалярное произведение

Скалярное произведение полезно тем, что дает косинус половины угла между двумя кватернионами, умноженный на их длину. Соответственно, скалярное произведение двух единичных кватернионов даст косинус половины угла между двумя ориентациями. Угол между кватернионами — это угол поворота из q в q’ (по кратчайшей дуге).

Видео:9 класс, 33 урок, ПоворотСкачать

Вращение 3d вектора

Вращение 3d вектора v кватернионом q определяется как

причем вектор конвертируется в кватернион как

и кватернион обратно в вектор как

Видео:Параллельный перенос. Симметрия. Поворот | МатематикаСкачать

Умножение кватернионов

Одна из самых полезных операций, она аналогична умножению двух матриц поворота. Итоговый кватернион представляет собой комбинацию вращений — сначала объект повернули на q, а затем на q’ (если смотреть из глобальной системы координат).

Примеры векторного и скалярного перемножения 2-х векторов векторное произведение — вектор: Скалярное произведение — число:

Пример умножения 2-х кватернионов:

Видео:Unity C#. Transform RotateAround. Справочник. Мусин Михаил.Скачать

Конвертирование между кватернионом и Axis Angle представлением

В разделе Axis Angle представление вращения была сделана неудачная попытка объединить 3 Axis Angle представления в одно . Это можно сделать опосредовано. Сначала Axis Angle представления конвертируются в кватернионы, затем кватернионы перемножаются и результат конвертируется в Axis Angle представление.

Пример конвертирования произведения 2-х кватернионов в Axis Angle представление:

Фрагмент программы на C:

Видео:Кинематика вращательного движения. Часть 2. Матрица поворота.Скачать

Конвертирование кватерниона в матрицу поворота

Матрица поворота выражается через компоненты кватерниона следующим способом:

где

Проверим формулы конвертирования на примере конвертирования произведения 2-х кватернионов в матрицу поворотов:

Определяем элемент матрицы m[0][0] через параметры кватерниона:

Соответствующее произведению кватернионов (q1 и q2) произведение матриц поворотов было получено ранее (см. Матрицы поворота и углы Эйлера):

Как видим, результат m[0][0], полученный через конвертирование, совпал с значением в матрице поворота.

Фрагмент программного кода на С для конвертирования кватерниона в матрицу поворота:

При конвертировании используется только умножения и сложения, что является несомненным преимуществом на современных процессорах.

Часто для задания вращений используют только кватернионы единичной длины, но это не обязательно и иногда даже не эффективно. Разница между конвертированием единичного и неединичного кватернионов составляет около 6-ти умножений и 3-х сложений, зато избавит во многих случаях от необходимости нормировать (приводить длину к 1) кватернион. Если кусок кода критичен по скорости и вы пользуетесь только кватернионами единичной длины тогда можно воспользоваться фактом что норма его равна 1.

Видео:8.1. Поворот системы координатСкачать

Конвертирование матрицы поворота в кватернион

Конвертирование матрицы в кватернион выполняется не менее эффективно, чем кватерниона в матрицу, но в итоге мы получим кватернион неединичной длины. Его можно нормализовать.

Фрагмент программного кода конвертирования матрицы поворота в кватернион:

📸 Видео

Алгебра 10 класс Поворот точки вокруг начала координат СеминарСкачать