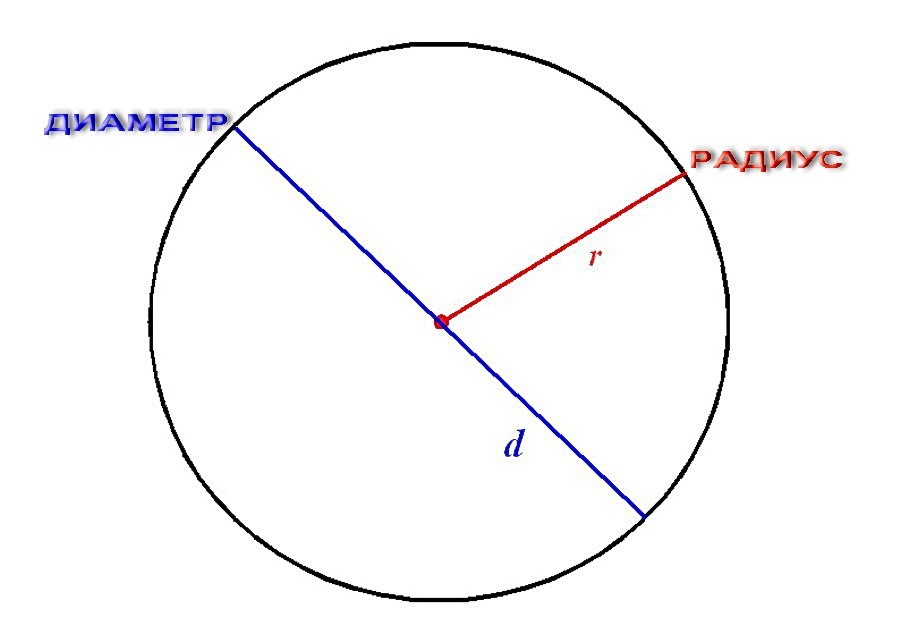
Диаметр и окружность это одно и тоже или нет (4 видео)

Разница между окружностью, диаметром и радиусом

Окружность против диаметра против радиуса Радиус, диаметр и длина окружности — это измерения трех важных свойств круга.Диаметр и радиусКруг определяется как геометрическое место точки на постоянном

Содержание

Содержание:
Круг. Окружность (центр, радиус, диаметр)
Окружность и диаметр одно и тоже или нет
Диаметр и радиус — что это такое?
Понятия радиус и диаметр
Как использовать эти понятия в жизни
Другие понятия
Разница между окружностью, диаметром и радиусом
Содержание:
Круг. Окружность (центр, радиус, диаметр)
📹 Видео

Видео:РАДИУС ОКРУЖНОСТЬ ДИАМЕТР КРУГ / 3 КЛАСС МАТЕМАТИКА. ЧТО ТАКОЕ ОКРУЖНОСТЬ ? ЧТО ТАКОЕ РАДИУС ?Скачать

Содержание:

Окружность против диаметра против радиуса

Радиус, диаметр и длина окружности — это измерения трех важных свойств круга.

Диаметр и радиус

Круг определяется как геометрическое место точки на постоянном расстоянии от фиксированной точки на двумерной плоскости. Фиксированная точка называется центром. Постоянная длина называется радиусом. Это кратчайшее расстояние между центром и локусом. Отрезок, начинающийся от геометрического места, проходящий через центр и заканчивающийся на геометрическом месте, известен как диаметр.

Радиус и диаметр — важные параметры круга, потому что они определяют размер круга. Чтобы нарисовать круг, требуется только радиус или диаметр.

Диаметр и радиус математически связаны следующей формулой

D = 2r

где D это diameter и r эторадиус.

Длина окружности

Геометрическое место точки называется окружностью. Окружность представляет собой изогнутую линию, длина которой зависит от радиуса или диаметра. Математическое соотношение между радиусом (или диаметром) и окружностью задается следующей формулой:

С = 2πr = πD

куда C — длина окружности и π = 3,14. Греческая буква число Пи (π) является константой и играет важную роль во многих математических и физических системах. Это иррациональное число имеет значение 3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 …… В большинстве случаев число пи с точностью до двух знаков после запятой, то есть π = 3,14, равно достаточно для значительной точности.

Часто в школьной математике среднего уровня вышеприведенная формула используется для определения константы число Пи (π) как отношение диаметра круга к его длине окружности, где его значение приблизительно дается как дробь 22/7.

В чем разница между окружностью, радиусом и диаметром?

• Радиус и диаметр — прямые линии, а окружность — замкнутая кривая.

• Диаметр в два раза больше радиуса.

• Окружность равна 2π, умноженному на радиус круга, или π умноженному на диаметр круга.

Видео:Длина окружности. Математика 6 класс.Скачать

Круг. Окружность (центр, радиус, диаметр)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.

Видео:Радиус и диаметрСкачать

Окружность и диаметр одно и тоже или нет

Видео:Окружность и круг, 6 классСкачать

Диаметр и радиус — что это такое?

В жизни человек часто сталкивается с понятием окружность. Все едят с круглых тарелок, грызут круглые яблоки, катаются на велосипеде или ездят на транспорте с круглыми колесами и просто видят круглое солнце.

Видео:Длина окружности. Площадь круга. 6 класс.Скачать

Понятия радиус и диаметр

Немногие задумываются, что на самом деле круг – очень сложная замкнутая фигура. Она состоит из главной точки (так называемый центр), а также из множества точек, которые идут от этого центра. Расстояние от центральной точки до окружности называют радиус. Чаще всего это понятие обозначается букой «R».

Если соединить две противоположные друг другу точки окружности и провести между ними линию, то она и будет диаметром. Диаметр обозначают символом «Ø». То есть радиус всегда будет равен половине диаметра.

Видео:Окружность. Как найти Радиус и ДиаметрСкачать

Как использовать эти понятия в жизни

Вообще с этими понятиями знакомы практически все, кто учил геометрию в школе. Взрослые тоже часто сталкиваются с ними, когда помогают детям делать домашнее задание или просто проверяют его.

Также эти понятия очень часто используются в черчении, к примеру, в архитектуре, когда планируется сделать круглое окно, арку или другую круглую деталь.

В ландшафте тоже не обойтись без радиуса и диаметра, ведь именно они позволят поделить круг на несколько частей, создав яркие цветочные композиции. Последние будут не только радовать глаза, но и помогут отвлечь внимание гостей от грядок с овощами.

Во время конструирования одежды тоже часто встречаются понятия радиус и диаметр. Например, когда шьют шляпы, юбки или круглые накладные воротники.

Понятия диметр и радиус часто используются в программировании и создании сайтов. К примеру, многие создают программы для коррекции кругов (последние используются в разных сферах).

Важно обратить внимание, что понятия диаметр и радиус касаются не только круга. Круг – это фигура, которая лежит на определенной плоскости. Но в геометрии фигуры не всегда лежат на плоскости, некоторые находятся в пространстве. И понятия круг в пространстве вообще не существует, в нем используются объемные фигуры, например, эллипс, цилиндр, конус или шар. Для вычисления объема всех этих фигур тоже понадобится определять диаметр и радиус.

Видео:Окружность, диаметр, хорда геометрия 7 классСкачать

Другие понятия

Существует еще несколько понятий, которые могут пригодиться тем, кто работает с диаметром или радиусом:

Дуга. Это кривая линия, которая является частью окружности. Ее измеряют в градусах. Сумма всех дуг составляет 360 градусов.
Хорда. В отличие от кривой дуги это прямой отрезок, который соединяет две точки на окружности. Хорда отличается и диаметра – последний всегда равен двум радиусам и всегда проходит через центральную точку круга. Хорда же может быть длиннее или короче радиуса и никогда не проходит через центральную точку на круге.
Сектор. Простыми словами, круг – это торт или пирог. Сектор же это треугольный кусок, который вырезается из этого пирога или торта.
Касательная. Это линия, которая проходит рядом с кругом так, что соприкасается только с одной точкой на окружности.

Все перечисленные выше понятия пригодятся не только тем, кто учит геометрию, но и тем, кто имеет дело с кругами в других сферах. В математике существует несколько формул, которые помогут выяснить величину любого из описанных выше понятий по заданным параметрам.

Видео:Длина окружности. Площадь круга - математика 6 классСкачать