- Треугольники, четырёхугольники, многоугольники и их элементы
- Теория к заданию №18
- Разбор типовых вариантов задания №18 ОГЭ по математике
- Первый вариант задания
- Второй вариант задания
- Третий вариант задания
- Демонстрационный вариант ОГЭ 2019
- Четвертый вариант задания
- Пятый вариант задания
- Задание №18 ОГЭ по математике
- Задание 18 ОГЭ по Математике. Треугольники, четырёхугольники, многоугольники и их элементы
- 🌟 Видео
Видео:ОГЭ 2022 по математике. Задания 17,18. Площадь четырехугольников, кругаСкачать

Треугольники, четырёхугольники, многоугольники и их элементы
В 18 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства.
В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры.
Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора?
С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить
заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Ответом в задании 16 является целое число или конечная десятичная дробь.
Теория к заданию №18
Приступим к разбору теории.
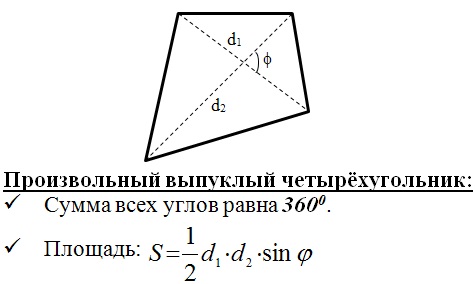
Выпуклый четырехугольник:
Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.
Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:
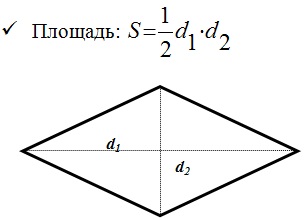
Разберем пример четырехугольника — ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.
Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.
Ниже я разобрал типовые примеры 11 задания. Давайте приступим к их рассмотрению.
Разбор типовых вариантов задания №18 ОГЭ по математике
Первый вариант задания
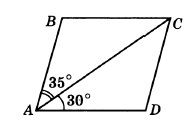
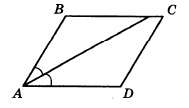
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
Решение:
Найдем угол BAD — это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
∠ABC = ∠ADC = 180 — 65 = 115°
Так как нас просят найти меньший угол, то это 65.
Второй вариант задания
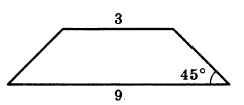
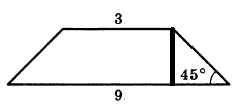
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.
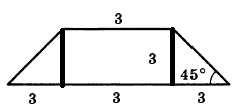
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Третий вариант задания
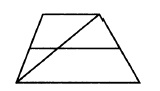
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
Так как нас просят найти больший из отрезков, то ответ 5,5.
Демонстрационный вариант ОГЭ 2019
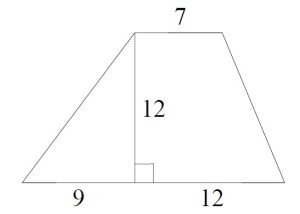
Найдите площадь трапеции, изображённой на рисунке.
Решение:
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это
«полусумма оснований умноженная на высоту»
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²
Четвертый вариант задания
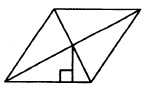
Сторона ромба равна 4, а расстояние от точки пересечения диагоналей ромба до неё равно 1. Найдите площадь ромба.
Решение:
Площадь ромба будем искать по формуле:
где a – сторона ромба, h– высота, опущенная на сторону а.
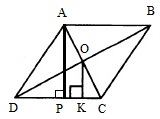
Найдем h. Для этого рассмотрим ∆ОКС и ∆АРС:
Здесь ОК || АР, причем ОК проходит через середину АС (т.к. АВСD ромб, то его диагонали в т.О делятся пополам). Значит, ОК – ср.линия ∆АРС. Поэтому АР=2ОК. Т.к. пор условию ОК=1, то АР=2·1=2. Т.о., h=АР=2.
Пятый вариант задания
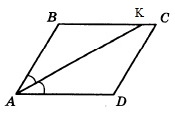
Найдите величину острого угла параллелограмма АВСD, если биссектриса угла А образует со стороной ВС угол, равный 41 0 . Ответ дайте в градусах.
Решение:
Т.к. АК биссектриса, то углы ВАК и КАD равны. Обозначим ∠ВАК через х.
Поскольку АВСD параллелограмм, то ∠В+∠А=180 0 . Т.к. АК биссектриса, то ∠А=2х. Тогда ∠В=180 0 –2х.
По теореме о сумме углов треуг-ка ∠ВАК+∠В+∠ВКА=180 0 .
Видео:Ты точно получишь 1 балл по геометрии за это задание. Все типы задания №18 на ОГЭ по математике!Скачать

Задание №18 ОГЭ по математике
В 18 задании необходимо найти какую-либо часть фигуры, нарисованной на клетчатой бумаге. Именно клетчатая бумага 1×1 является особенностью данного задания. Задание не сложное, необходимо внимательно посчитать количество клеток и при необходимости выполнить действие. Опять же нам понадобятся элементарные знания геометрии для успешного решения данного задания. Ниже я разобрал типичные задания.
Внимательно смотрим на рисунок и видим, что длина одной диагонали ромба равна 2, а второй 4. Так как нас спрашивают длину большей диагонали, то в ответе нужно указать 4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Мы знаем, что средняя линия равна полусумме оснований. Нижнее основание данной трапеции равно 8
Клетка — структурно-функциональная элементарная единица строения и жизнедеятельности всех организмов.
pазбирался: Даниил Романович | обсудить разбор | оценить
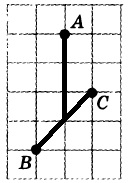
Проведем необходимые отрезки:
Из рисунка можно вычислить длину — это 3.
pазбирался: Даниил Романович | обсудить разбор | оценить
Детализируем рисунок. Проведем вертикальную линию, которая отсекает от сторон угла 2 клетки по горизонтали . В результате получен прямоугольный ∆АВС: 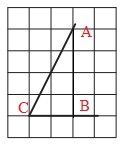
По рисунку подсчитываем длины отрезков АВ и ВС (по кол-ву клеток):
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь параллелограмма вычисляется так:
Обозначим a и ha на рисунке: 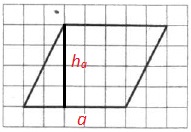
Вычисляем искомую площадь:
pазбирался: Даниил Романович | обсудить разбор | оценить
Площадь ромба будем искать через его диагонали:
Линии диагоналей обозначим на рисунке красным: 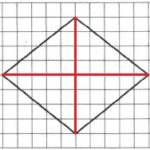
Находим площадь фигуры:
pазбирался: Даниил Романович | обсудить разбор | оценить
На клетчатой бумаге с размером клетки 1х1 изображен треугольник АВС. Найти длину его средней линии, параллельной стороне АС.
Для решения задачи надо вспомнить свойство средней линии: она параллельна основанию и равна его половине. Следовательно, чтобы найти длину средней линии, надо сторону треугольника разделить пополам. Найдем сторону треугольника, которой параллельна средняя линия, т.е. АС, сосчитав клетки, получим, что АС равна 8. Значит, средняя линия равна 8:2=4.
pазбирался: Даниил Романович | обсудить разбор | оценить
Видео:Задание 18 все типы | МАТЕМАТИКА ОГЭ 2023Скачать

Задание 18 ОГЭ по Математике. Треугольники, четырёхугольники, многоугольники и их элементы
7. Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
Решение.
∠BAD = 35° + 30° = 65°
В параллелограмме противоположные углы равны, а сумма соседних 180°.
Значит, ∠ABC = ∠ADC = 180° — 65° = 115°
8. Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение.
Средняя линия трапеции является также и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны , то есть 5, и .
Наш онлайн-курс по Физике
Все темы ЕГЭ с нуля
Можно не только читать, но и смотреть новые объяснения и разборы на нашем YouTube канале!
Пожалуйста, подпишитесь на канал и нажмите колокольчик, чтобы не пропустить новые видео
Задавайте свои вопросы в комментариях и оставляйте задачи, которые вы хотите, чтобы мы разобрали.
Мы обязательно ответим!
Мы заметили, что Вы регулярно пользуетесь нашими материалами для подготовки по физике.
Результат будет выше, если готовиться по отработанной методике.
У нас есть онлайн-курсы как для абитуриентов, так и для преподавателей.
🌟 Видео
ОГЭ 2023 по математике. Летний курс. Геометрия. Площадь треугольника и четырехугольника. Решение №18Скачать

Задание 18 (часть 1) | ОГЭ 2024 Математика | Фигуры на квадратной решёткеСкачать

18 задание ОГЭ по математикеСкачать

ГЕОМЕТРИЯ ОГЭ задание 18 найти площадь четырехугольника с заданными координатами вершинСкачать

Все типы 18 задания ОГЭ математика 2023 | Молодой РепетиторСкачать

ОГЭ 2021. Задание 18. Фигуры на квадратной решеткеСкачать
Задание №18 ОГЭ математика 2024Скачать

18 ЗАДАНИЕ ОГЭ НАЙТИ ПЛОЩАДЬ ТРЕУГОЛЬНИКАСкачать

Геометрия на клетчатой бумаге | Задание 18 ОГЭ | Математика ОГЭ | Площади фигур | МегаШколаСкачать

ОГЭ, математика, задание 18| Треугольник на клетчатой бумагеСкачать
17 задание огэ по математикеСкачать

ОГЭ по математике 2019. Задание 18. Площади фигур. Теория+задачи (часть 1)Скачать

19 задание ОГЭ по математикеСкачать

Пятнадцатое задание ОГЭ по математике(13) #огэ #огэ2023 #огэпоматематике #математика #огэматематикаСкачать

ОГЭ 2024. Математика. Вариант 18. 50 вариантов. Под ред. И.В. Ященко. Задания 1 - 19Скачать

ЗАДАНИЯ НА КЛЕТЧАТОЙ БУМАГЕ (ЯЩЕНКО) | ВСЕ ТИПЫ №18 | ОГЭ ПО МАТЕМАТИКЕ 2023 | ч.1Скачать

задание 18.ОГЭСкачать