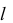Поверхность образованная вращением дуги окружности (6 видео)

Поверхность образованная вращением дуги окружности

Рассмотрим поверхность вращения, образованную вращением дуги плоской кривой АВ вокруг оси, лежащей в ее плоскости, примем ось вращения за ось Ох. Центр тяжести, очевидно, лежит на этой оси, являющейся осью симметрии; остается, следовательно, только определить положение центра тяжести на оси.

Проведем ось Оу перпендикулярно к Ох в плоскости кривой. Пусть — абсциссы концов дуги АВ, и

Пусть — площадь поверхности вращения, — бесконечно малый элемент поверхности с абсциссой Абсцисса искомого центра тяжести определяется общей формулой (п° 216):

Сначала можно просуммировать все элементы имеющие одну и ту же абсциссу и заключенные между двумя плоскостями, перпендикулярными к с абсциссами Эти плоскости вырезают на дуге АВ элемент а сумма рассматриваемых элементов равна поверхности, образованной вращением элемента кривой, имеющего

ординату у. Эта поверхность представляет собой полосу шириной и длиной ее площадь равна поэтому . После этого остается лишь просуммировать по всем элементам и формула приобретает вид:

С другой стороны, площадь равна сумме площадей всех полос:

Применим эти формулы к частному случаю.

Содержание

227. Сферический пояс.
228. Теоремы Гюльдена.
229. Поверхность и объем тора.
Поверхности вращения
Поверхности вращения в начертательной геометрии с примерами
Поверхности вращения
Пересечение поверхностей вращения плоскостью
Развертки поверхностей вращения
Приближенные развертки
Условные развертки
💥 Видео

227. Сферический пояс.

Сферическим поясом называют часть поверхности сферы, заключенную между двумя параллельными плоскостями. Сферический пояс представляет собой, следовательно, поверхность, образованную вращением, дуги АВ окружности вокруг диаметра . Его площадь и центр тяжести определяются поэтому предыдущими формулами.

Пусть а — радиус, тогда уравнение окружности будет

Пусть — абсциссы двух параллельных плоскостей, проведенных через концы А и В образующей дуги пояса;

формулы предыдущего п° принимают вид:

отсюда, разделив эти равенства почленно, получим:

Итак, центр тяжести сферического пояса лежит в середине отрезка, соединяющего центры двух оснований.

228. Теоремы Гюльдена.

Пусть АВ есть дуга плоской кривой, отнесенной к двум прямоугольным осям Ох и Оу. Ордината центра тяжести дуги определяется формулой

где интеграл распространен по дуге АВ.

С другой стороны, площадь поверхности вращения S, образованной той же дугой при ее вращении вокруг Ох, равна

Исключая интеграл, получаем

Отсюда имеем первую теорему Гюльдена:

Площадь поверхности, образованной вращением дуги плоской кривой вокруг прямой, лежащей в ее плоскости, равна произведению длины дуги на длину окружности, описанной ее центром тяжести,

Рассмотрим далее плоскую фигуру с площадью S, отнесенную к двум прямоугольным осям ордината ; ее центра тяжести определяется формулой

где интеграл распространен на все элементы dS площади S.

Предположим, что площадь S заставляют вращаться вокруг оси Ох. Допустим при этом, что площадь S целиком расположена по одну сторону от этой оси. Элемент площади с ординатой у опишет кольцевой бесконечно тонкой объем, измеряемый произведением площади его сечения на его длину .

Объем V тела, образованного вращением всей площади S, выразится интегралом от всех элементарных объемов:

Исключая из двух предыдущих равенств интеграл, получим:

Отсюда имеем вторую теорему Гюльдена:

Объем, образованный вращением плоской фигуры вокруг оси, лежащей в плоскости фигуры вне ее, равен произведению площади фигуры S на длину окружности, описанной ее центром тяжести.

229. Поверхность и объем тора.

Теоремы Гюльдена позволяют непосредственно определить поверхность и объем тора.

Тор есть кольцевая фигура, образованная вращением круга радиуса а вокруг прямой, расположенной в плоскости круга на расстоянии от его центра. Геометрический центр круга есть в то же время его центр тяжести; при вращении вокруг оси он опишет окружность

длиной Длина окружности и площадь образующего круга равны соответственно

Площадь поверхности тора равна поэтому, на основании первой теоремы Гюльдена:

объем тора, в силу второй теоремы Гюльдена, равен:

Видео:Поверхность вращения.Скачать

Поверхности вращения

Поверхность, образованная вращением какой-либо линии I вокруг оси /, называется поверхностью вращения (рис. 67). Линия / называется её образующей. Каждая точка образующей при вращении в пространстве описывает окружность, плоскость которой перпендикулярна оси. Поэтому если ось — проецирующая, то на модели одна из проекций поверхности вращения изображается в виде окружности. Контур другой проекции повторяет форму образующей (рис. 68).

Контуры, ограничивающие изображение поверхности вращения, называются очерками. Очерки разных полей соответственными не являются.

Поверхность, образованная вращением окружности вокруг её диаметра, называется сферической. На эпюре она изображается окружностями одинакового радиуса, но очерки в каждом поле разные (рис. 69).

Поверхность, образованная вращением окружности или её дуги вокруг оси, не совпадающей с диаметром, называется торовой (рис 70).

Тор, представленный на рис. 70, а, образован вращением целой окружности вокруг оси i ± я₂. На горизонтальной проекции внешний очерк тора представляет собой траекторию движения точки А, внутренний очерк — траекторию движения точки В, осевая линия — траекторию движения центра О окружности. Поверхность, образованная вращением выпуклой дуги окружности вокруг оси / _L л₂, показана на рис. 70, б. Вращением вогнутой дуги окружности образована поверхность, изображённая на рис. 70, в.

Прямой круговой конус и прямой круговой цилиндр

При вращении прямой линии вокруг оси образуется прямой круговой конус, если прямая пересекает ось, или прямой круговой цилиндр, если прямая параллельна оси. Их модели показаны на рис. 71, 72.

На всех чертежах показаны проекции очерков и очерковых образующих поверхностей.

Конус и цилиндр можно рассматривать и как линейчатые, и как поверхности вращения.

Поверхности, образующие или рёбра которых перпендикулярны плоскости проекций, называются проецирующими. Такими являются прямой цилиндр и прямая призма.

Видео:Лекция 5.Поверхности вращения. Часть 5.Скачать

Поверхности вращения в начертательной геометрии с примерами

Содержание:

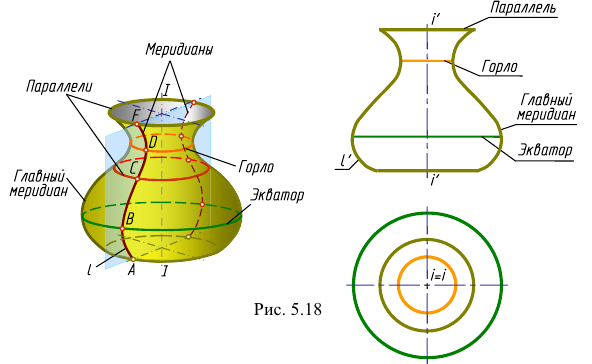
Поверхностей вращения существует множество: цилиндр, конус, сфера, эллипсоиды, торы и др. Поверхность вращения общего вида образуется вращательным перемещением образующей линии вокруг неподвижной оси. Каждая точка образующей линии при вращении вокруг неподвижной оси описывает окружность с центром на оси вращения. Эти окружности называются параллелями.

Наибольшую из параллелей (окружностей) поверхности вращения называют экватором поверхности, а наименьшую — горлом (шейкой) поверхности. Плоскости, проходящие через ось поверхности вращения, называют меридиональными, а линии, по которым они пересекают поверхность, — меридианами. Меридиональная плоскость, параллельная плоскости проекции, называется плоскостью главного меридиана, а линия пересечения этой плоскости с поверхностью вращения называется главным меридианом.

Видео:Лекция 5. Поверхности вращения. часть 1.Скачать

Поверхности вращения

Поверхностью вращения называется поверхность, описываемая кривой (или прямой) образующей при ее вращении вокруг неподвижной оси (рис. 5.18). Эта поверхность определяется на чертеже заданием образующей и оси вращения.

Каждая точка образующей

Плоскость, проходящую через ось поверхности вращения, называют меридиональной. Линию ее пересечения с поверхностью — меридианом. Меридиан, параллельный фронтальной плоскости проекций, называется главным меридианом. Все меридианы равны между собой.

На чертеже ось вращения располагают перпендикулярно к одной из плоскостей проекций, например горизонтальной. Тогда все параллели проецируются на эту плоскость в истинную величину. Экватор и горло определят горизонтальный очерк поверхности. Фронтальным очерком такой поверхности будет главный меридиан, то есть меридиан, расположенный во фронтальной плоскости.

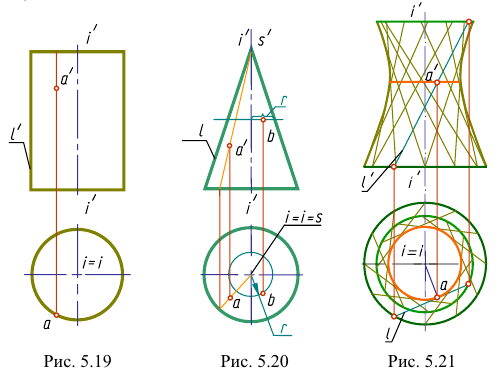
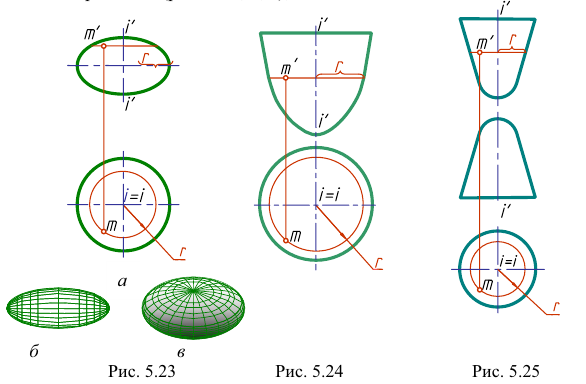
Точки на поверхностях вращения могут быть построены с помощью параллелей, то есть окружностей на поверхности (рис. 5.20, рис. 5.22, а, б, в, рис. 5.23 — рис. 5.25).

Рассмотрим некоторые тела и поверхности вращения.

1 .Поверхности, образованные вращением прямой линии:

а) цилиндр вращения — поверхность, полученная вращением прямой вокруг параллельной ей оси (рис. 5.19);

б) конус вращения — поверхность, образованная вращением прямой вокруг пересекающейся с ней осью (рис. 5.20);

в) однополостный гиперболоид вращения — поверхность, полученная вращением прямой вокруг скрещивающейся с ней осью (рис. 5.21).

Точка А, лежащая на перпендикуляре к оси вращения и образующей, будет описывать наименьшую окружность, являющуюся горлом гиперболоида. Однополостный гиперболоид может быть также получен вращением гиперболы вокруг ее мнимой оси.

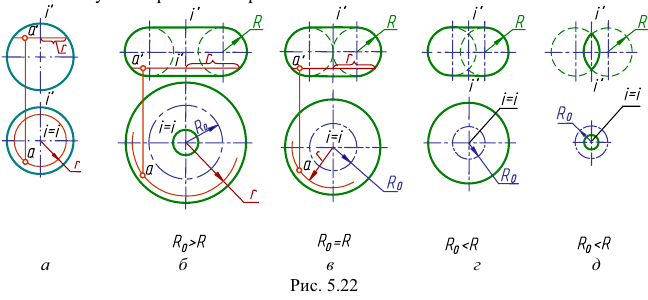
2. Поверхности, образованные вращением окружности вокруг неподвижной оси: а) сфера — поверхность, полученная вращением окружности вокруг ее диаметра (рис. 5. 22, а);

б) тор — поверхность, полученная вращением окружности вокруг оси лежащей в плоскости этой окружности, но не проходящей через ее центр (рис. 5.22, б-д).

Если ось вращения проходит вне окружности, то поверхность называется «открытый тор» или «тор — кольцо» (рис. 5.22, б); если ось касается окружности, то образованная поверхность называются «закрытый тор» (рис. 5.22, в); если ось пересекает окружность — «самопересекающийся тор» (рис. 5.22, г, д)). Тор, изображенный на рис. 5.22, г, называется также «тор-яблоко», а на рис. 5.22, д — «тор-лимон». Сфера — частный случай торовой поверхности.

3. Поверхности вращения, образованные вращением кривых второго порядка:

а) эллипсоид вращения — поверхность, полученная вращением эллипса вокруг оси (рис. 5.23). Поверхность, образованная вращением эллипса вокруг его большой оси, называется вытянутым эллипсоидом вращения (рис. 5.23, б), при вращении вокруг малой оси — сжатым элипсоидом вращения (рис. 5.23, а, в);

б) параболоид вращения — поверхность, образованная вращением параболы вокруг ее оси (рис. 5.24);

в) двухполостный гиперболоид вращения — поверхность, образованная вращением гиперболы вокруг ее действительной оси (рис. 5.25).

Пересечение поверхностей вращения плоскостью

При пересечении поверхности вращения плоскостью получается линия сечения — плоская фигура. Построение проекций линии пересечения необходимо начинать с определения опорных точек. К ним относятся точки, расположенные на очерковых образующих поверхности (точки, определяющие границы видимости проекций кривой), и точки, удаленные на экстремальные (максимальное и минимальное) расстояния от плоскостей проекций. После этого определяют произвольные (промежуточные) точки линии пересечения.

Для определения точек, принадлежащих линии пересечения, можно использовать различные методы. Один из них — метод вспомогательных секущих плоскостей. Суть его заключается в том, что заданные плоскость и поверхность вращения пересекают вспомогательными плоскостями. Находят линии пересечения этой плоскости с заданными плоскостью и поверхностью вращения. Затем отмечают точки, в которых пересекаются полученные линии пересечения. Построенные точки фигуры сечения соединяют плавной кривой линией.

Развертки поверхностей вращения

Построение разверток поверхностей вращения имеет большое значение, особенно при конструировании из листового материала моделей различных сооружений, форм для металлических отливок, сосудов, трубопроводов, резервуаров и т.п.

Приближенные развертки

Поверхности, которые можно совместить с плоскостью без разрывов и складок, называют развертывающимися поверхностями. Фигуру, полученную при совмещении развертывающейся поверхности с плоскостью, называют разверткой. Для развертывающихся поверхностей можно построить приближенную развертку (условно-развертываемые поверхности). При построении приближенной развертки поверхность аппроксимируют поверхностями вписанных или описанных многогранников, имеющих грани в форме прямоугольников или треугольников. Поэтому при графическом выполнении разверток поверхности всегда приходится производить разгибание или спрямление кривых линий, принадлежащих поверхности, что неизбежно приводит к потере точности.

Условные развертки

Неразвертывающиеся поверхности не могут быть совмещены сплоскостью без разрывов и складок, т.е. теоретически они не имеют своей развертки. Поэтому говорят лишь об условном решении задачи по построению разверток неразвертывающихся поверхностей. На практике для получения развертки неразвертываемой поверхности, выполненной из листового материала, приходится кроме изгибания производить растяжение и сжатие определенных участков листа.

Построение условной развертки неразвертывающейся поверхности состоит в том, что отсеки заданной поверхности аппроксимируются отсеками развертывающихся поверхностей — гранными, цилиндрическими или коническими.

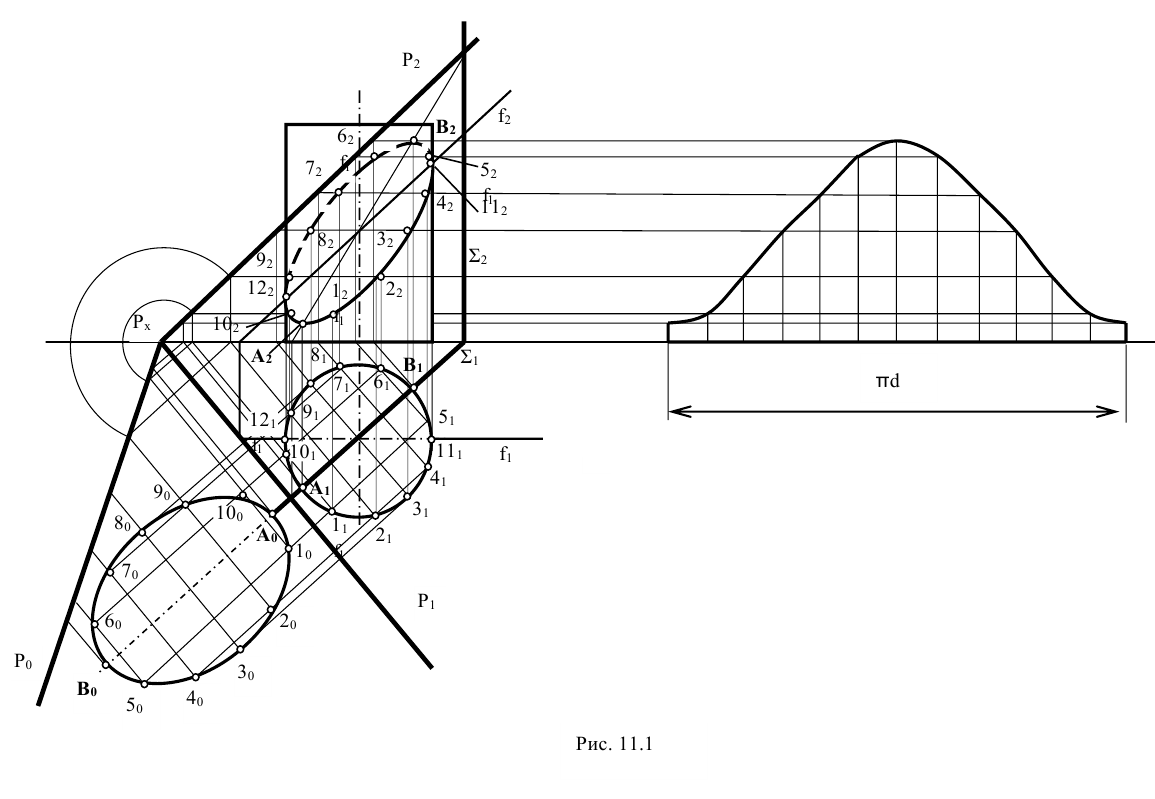
Задание: построить проекции и натуральный вид фигуры сечения поверхности цилиндра плоскостью Р (рис. 11.1). Построить развёртку боковой поверхности усечённой части цилиндра.

Решение: на рисунке 11.1 изображены прямой круговой цилиндр, основание которого принадлежит горизонтальной плоскости проекций и секущая плоскость Р общего положения. Поскольку секущая плоскость наклонена к оси цилиндра, то боковая поверхность цилиндра пересекается по эллиптической кривой.Форма сечения в этом случае зависит от того, пересекает ли плоскость Р основания цилиндра. В рассматриваемом случае секущая плоскость Р не пересекает оснований цилиндра. Это видно из того, что горизонтальная проекция нижнего основания не пересекается с горизонтальным следом плоскости Р, а горизонтальная проекция горизонтали , по которой плоскость Р пересекается с плоскостью верхнего основания, не пересекает его горизонтальную проекцию.

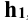
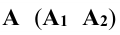
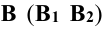
Для нахождения эллипса сечения плоскости Р с боковой поверхностью цилиндра находят сначала его низшую и высшую точки.

Эти точки являются концами большой оси эллипса сечения и лежат на линии наибольшего наклона плоскости Р к горизонтальной плоскости проекций. Следовательно, прямая АВ перпендикулярна к горизонтальному следу плоскости Р и пересекает ось цилиндра.

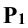
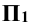
Для нахождения точек А и В проводят плоскость Σ, перпендикулярную к горизонтальному следу и проходящую через ось цилиндра. Эта плоскость перпендикулярна к плоскости . Затем находят линию пересечения плоскостей Р и Σ.

Боковая поверхность цилиндра является горизонтально проецирующей и поэтому проецируется на горизонтальную плоскость проекций в окружность. Так как отрезок АВ является частью линии пересечения плоскостей Р и Σ, а точки А и В лежат на боковой поверхности цилиндра, то горизонтальные проекции точек А и В должны лежать на одной окружности и на горизонтальной проекции прямой пересечения плоскостей Р и Σ. По горизонтальным проекциям точек А и В находят их фронтальные проекции, исходя из условия, что точки А и В лежат на найденной прямой пересечения плоскостей Р и Σ.

Для определения остальных точек эллипса сечения на цилиндрической поверхности выбирают ряд образующих. За первую образующую выбирают ту, на которой лежит точка А. Остальные образующие получают делением окружности (горизонтальной плоскости цилиндрической поверхности) на 12 равных частей (можно делить на другое количество частей). Затем находят точки пересечения образующих с плоскостью Р. В рассматриваемом примере все образующие перпендикулярны к горизонтальной плоскости проекций. Следовательно, горизонтальные проекции точек пересечения образующих с плоскостью Р совпадают с горизонтальными проекциями самих образующих.

Далее наносят горизонтальные проекции точек пересечения образующих с плоскостью Р (1, 2, 3, 4, 5, 6, 7, 8, 9, 10) и находят фронтальные проекции этих точек, проводя через них горизонтали в плоскости.

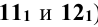
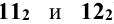
Кривая линия, ограничивающая фронтальную проекцию фигуры сечения, включает видимые и невидимые участки. Точки, являющиеся границей видимости кривой, лежат на очерковых образующих. Отмечают горизонтальные проекции этих точек () и находят фронтальные проекции (), проводя через эти точки в плоскости Р горизонтали. Полученные точки соединяют плавной кривой линией. Кривая от точки 12 через точки 10, А, 1, 2, 3, 4 до точки 11 на фронтальной плоскости проекций является видимой, а остальная часть — невидимой.

Видимую часть кривой обводят сплошной линией, а невидимую — штриховой. Малой осью эллипса сечения является отрезок 3 — 8, проецирующийся в натуральную величину на горизонтальную плоскость проекций. Натуральная величина малой оси эллипса в рассматриваемом примере равна диаметру цилиндра. Натуральную величину эллипса сечения строят путём совмещения плоскости Р с горизонтальной плоскостью проекций.

Развёртка боковой поверхности прямого кругового цилиндра, не усечённого плоскостью, представляет собой прямоугольник с основанием, равным длине окружности основания цилиндра, и высотой, равной высоте цилиндра. При построении развёртки боковой поверхности цилиндра, пересечённого плоскостью, на развёртке необходимо наносить точки, принадлежащие линии пересечения, и затем эти точки соединять плавной кривой линией (рис. 11.1).

Для этого на развёртке боковой поверхности цилиндра проводят 12 образующих, отстоящих друг от друга на равном расстоянии. За первую образующую рекомендуется выбирать ту, на которой лежит точка А. Затем наносят на все образующие последовательно точки А, 1, 2, 3, 4, 11, 5, В, 6, 7, 8, 9, 12, 10. Расстояние от этих точек до нижнего (или верхнего) основания проецируется на фронтальную плоскость проекций в натуральную величину. Соединив полученные точки плавной кривой линией, получают развёртку боковой поверхности усечённой части цилиндра.

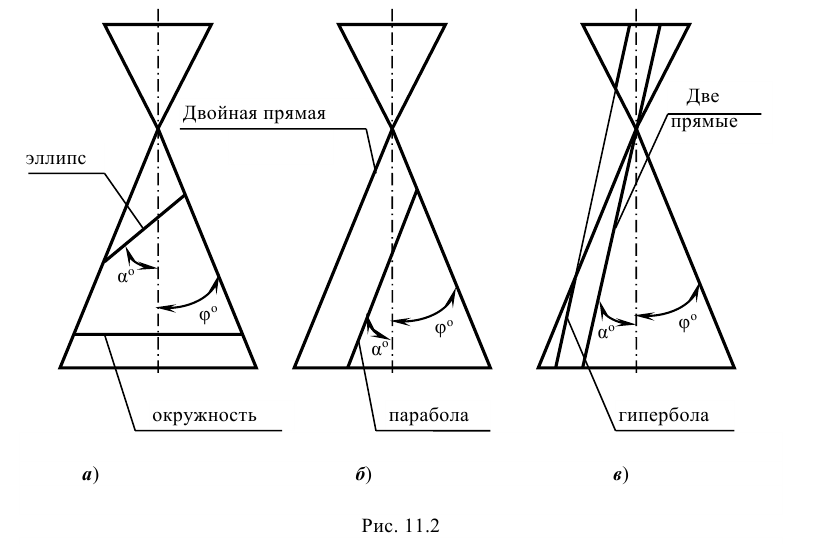
Задание: построить проекции и натуральную величину линии пересечения поверхности конуса плоскостью Р (рис. 11.3).

Решение: поверхность прямого кругового конуса относится к поверхностям вращения и является носителем кривых второго порядка: окружности, эллипса, параболы и гиперболы. Все эти кривые являются плоскими и, следовательно, могут быть получены в результате сечения конической поверхности плоскостью.

На рис. 11.2 приведены фронтальные проекции поверхности прямого кругового конуса, следы фронтально проецирующих секущих плоскостей и указан вид получаемой в сечении кривой. Можно установить признаки, обеспечивающие получение в сечении той или иной кривой второго порядка. Так, если обозначить угол наклона образующей конической поверхности к его оси через φ а угол между секущей плоскостью и той же осью через α , то можно утверждать, что при α > φ (рис. 11.2, а) в сечении получается эллипс (в частном случае, если α =90° — окружность), при α = φ (рис. 11.2, б) — парабола, и при α

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.