В прямоугольнике abcd через точку p проведена прямая km параллельная сторонам ad bc

Школе NET

Register

Do you already have an account? Login

Login

Don’t you have an account yet? Register

Newsletter

Submit to our newsletter to receive exclusive stories delivered to you inbox!

• Главная 
• Вопросы & Ответы 
• Вопрос 10258000

Таня Масян

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

В прямоугольнике ABCD через точку P проведены прямая KM, параллельная сторонам AD и BC, и прямая LN, параллельная сторонам AB и CD. Периметр прямоугольника KBLP равен 8 см, а периметр прямоугольника NPMD равен 18 см. Найдите периметр прямоугольника ABCD

Видео:Геометрия Через точку о пересечение диагоналей параллелограмма ABCD проведена прямая, пересекающаяСкачать

В прямоугольнике abcd через точку p проведена прямая km параллельная сторонам ad bc

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

На плане (см. рисунок) изображён район города, в котором проживает Вика. Сторона каждой клетки на плане равна 15 м. Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐центр. В 15 м от магазина расположен дом, где живёт одноклассник Вики Артём. В 30 м от детской площадки находится дом, где живёт Олег. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Через дорогу от дома дедушки расположен рынок, а недалеко от него – мебельный центр площадью 2025 м 2 .

Решение . Рядом с домом Вики, обозначенным на плане цифрой 4, находится одноэтажный магазин площадью 900 м 2 и фитнес‐центр. Значит, магазин отмечен цифрой 7, а фитнес-центр — цифрой 5. 30 м от детской площадки находится дом, где живёт Олег. Следовательно, дом, где живёт Олег, обозначен цифрой 1. Если выйти из фитнес‐центра, пройти небольшой ельник, обозначенный цифрой 6, и детскую площадку, то приходишь к угловому дому, где живёт дедушка Вики. Рядом с ним находится мастерская по ремонту бытовой техники. Значит, мастерская отмечена цифрой 2.

Видео:№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

Проверочная работа «16 задание ПРОФИЛЬ ЕГЭ математика»

Видео:Через середину К медианы ВМ треугольника АВС и вершину А проведена прямая пересекающая сторону ВС вСкачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

ПРОФИЛЬ ЕГЭ математика

1. Окружность, вписанная в ромб ABCD , касается сторон CD и BC в точках M и Q соответственно. Прямые AM и BC пересекаются в точке P.

а) Докажите, что

б) Найдите угол если DM = 4 и MC = 9.

2. Две окружности касаются внешним образом в точке C. Прямая касается меньшей окружности в точке A, а большей — в точке B, отличной от A. Прямая AC вторично пересекает большую окружность в точке D, прямая BC вторично пересекает меньшую окружность в точке E.

а) Докажите, что прямая AE параллельна прямой BD.

б) Пусть L — отличная от D точка пересечения отрезка DE с большей окружностью. Найдите EL, если радиусы окружностей равны 2 и 5.

3. В равнобедренной трапеции ABCD длины оснований AD и BC соответственно равны 4 и 3. Точки M и N лежат на диагонали BD, причем точка M расположена между точками B и N, а отрезки AM и CN перпендикулярны диагонали BD.

а) Докажите, что BN : DM = 3 : 4.

б) Найдите длину отрезка CN, если известно, что BM : DN = 2 : 3.

4. Дан треугольник ABC. Серединный перпендикуляр к стороне AB пересекается с биссектрисой угла BAC в точке K, лежащей на стороне BC.

а) Докажите, что

б) Найдите радиус окружности, вписанной в треугольник AKB , если а площадь треугольника AKC равна

5. Диагонали AC и BD четырёхугольника ABCD, вписанного в окружность, пересекается в точке P, причём BC = CD.

а) Докажите, что

б) Найдите площадь треугольника COD, где O — центр окружности, вписанной в треугольник ABD, если дополнительно известно, что BD — диаметр описанной около четырёхугольника ABCD окружности, AB = 6, а

6. Две окружности касаются внутренним образом. Третья окружность касается первых двух и их линии центров.

а) Докажите, что периметр треугольника с вершинами в центрах трёх окружностей равен диаметру наибольшей из этих окружностей.

б) Найдите радиус третьей окружности, если известно, что радиусы первых двух равны 6 и 2.

7. На окружности с центром O и диаметром MN, равным 34, взята точка K на расстоянии 15 от этого диаметра. Хорда KE пересекает радиус OM в точке F под углом, равным

а) Докажите, что KF : FE = 125 : 29.

б) Найдите площадь треугольника KEN.

8. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что ∠ ABM = ∠ DBC = ∠ MBD .

б) Найдите расстояние от точки О, точки пересечения диагоналей, до отрезка СМ, если BC = 42.

9. Две окружности касаются внутренним образом в точке С. Вершины A и B равнобедренного прямоугольного треугольника ABC c прямым углом C лежат на большей и меньшей окружностях соответственно. Прямая AC вторично пересекает меньшую окружность в точке D. Прямая BC вторично пересекает большую окружность в точке E.

а) Докажите, что AE параллельно BD.

б) Найдите AC, если радиусы окружностей равны 8 и 15.

10. Четырёхугольник ABCD вписан в окружность радиуса R = 10. Известно, что AB = BC = CD = 6.

а) Докажите,что прямые BC и AD параллельны.

ПРОФИЛЬ ЕГЭ математика

1. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.

б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если

2. В прямоугольном треугольнике ABC проведена высота CH из вершины прямого угла. В треугольники ACH и BCH вписаны окружности с центрами O₁ и O₂ соответственно, касающиеся прямой CH в точках M и N соответственно.

а) Докажите, что прямые AO₁ и CO₂ перпендикулярны.

б) Найдите площадь четырёхугольника MO₁NO₂, если AC = 20 и BC = 15.

3. В прямоугольную трапецию ABCD с прямым углом при вершине A и острым углом при вершине D вписана окружность с центром O. Прямая DO пересекает сторону AB в точке M, а прямая CO пересекает сторону AD в точке K.

а) Докажите, что

б) Найдите площадь треугольника AOM, если и

4. Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.

б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E, F последовательно расположены на окружности, а радиус окружности равен

5. Окружность с центром О₁ касается оснований ВС и AD и боковой стороны АВ трапеции ABCD. Окружность с центром O₂ касается сторон ВС, CD и AD. Известно, что АВ = 10, ВС = 9, CD = 30, AD = 39.

а) Докажите, что прямая О₁О₂ параллельна основаниям трапеции АВСD.

6. Треугольник ABC прямоугольный с прямым углом C. Проведена высота CH. На сторонах AC и BC соответственно отмечены точки M и N так, что угол MHN прямой.

а) Докажите, что треугольники и ABC подобны.

б) Найдите BN, если

7. На гипотенузе AB и на катетах BC и AC прямоугольного треугольника ABC отмечены точки M, N и K соответственно, причем прямая KN параллельна прямой AB и BM = BN = Точка P — середина отрезка KN.

а) Докажите, что четырехугольник BCPM — равнобедренная трапеция.

б) Найдите площадь треугольника ABC, если и

8. Две окружности с центрами O₁ и O₂ и радиусами 3 и 4 пересекаются в точках A и B. Через точку A проведена прямая MK пересекающая обе окружности в точках M и K, причем точка A находится между ними.

а) Докажите, что треугольники BMK и O₁AO₂ подобны.

б) Найдите расстояние от точки B до прямой MK, если O₁O₂ = 5, MK = 7.

9. Две окружности пересекаются в точках P и Q. Прямая, проходящая через точку P, второй раз пересекает первую окружность в точке A, а вторую — в точке D. Прямая, проходящая через точку Q параллельно AD, второй раз пересекает первую окружность в точке B, а вторую — в точке C.

а) Докажите, что четырёхугольник ABCD — параллелограмм.

б) Найдите отношение CP : PB, если радиус первой окружности втрое больше радиуса второй.

10. Дан равнобедренный треугольник ABC с основанием AC. Вписанная в него окружность с центром O касается боковой стороны BC в точке P и пересекает биссектрису угла B в точке Q.

а) Докажите, что отрезки PQ и OC параллельны.

б) Найдите площадь треугольника OBC, если точка O делит высоту BD треугольника в отношении BO : OD = 3 : 1 и AC = 2.

ПРОФИЛЬ ЕГЭ математика

1. Четырёхугольник ABCD вписан в окружность радиуса R = 8. Известно, что AB = BC = CD = 12.

а) Докажите,что прямые BC и AD параллельны.

2. В треугольнике MPK биссектриса угла K пересекает сторону MP в точке A. Окружность, описанная около треугольника AMK пересекает сторону PK в точке B.

а) Докажите, что треугольник ABM равнобедренный.

б) Найдите площадь треугольника ABM, если MK = 9, PK = 6, MP = 5.

3. К окружности с диаметром AB = 10 проведена касательная BC так что Прямая AC вторично пересекает окружность в точке D. Точка E диаметрально противоположна точке D. Прямые ED и BC пересекаются в точке F.

а) Докажите, что

б) Найдите площадь треугольника FBE.

4. Точка M лежит на стороне BC выпуклого четырёхугольника ABCD, причём B и C — вершины равнобедренных треугольников с основаниями AM и DM соответственно, а прямые AM и MD перпендикулярны.

а) Докажите, что биссектрисы углов при вершинах B и C четырёхугольника ABCD, пересекаются на стороне AD.

б) Пусть N — точка пересечения этих биссектрис. Найдите площадь четырёхугольника ABCD, если известно, что BM : MC = 3 : 4, а площадь четырёхугольника, стороны которого лежат на прямых AM, DM, BN и CN, равна 24.

5. Дана окружность с центром в точке O и радиусом 5. Точка K делит диаметр AD в отношении 1 : 9, считая от точки D. Через точку K проведена хорда BC перпендикулярно диаметру AD. На меньшей дуге AB окружности взята точка M.

а) Докажите, что BM · CM 2 .

б) Найдите площадь четырёхугольника ACBM, если дополнительно известно, что площадь треугольника BCM равна 24.

6. Дана равнобедренная трапеция ABCD с основаниями AD и BC. Окружность с центром O, построенная на боковой стороне AB как на диаметре, касается боковой стороны CD и второй раз пересекает большее основание AD в точке H, точка Q — середина CD.

а) Докажите, что четырёхугольник DQOH — параллелограмм.

б) Найдите AD, если ∠ BAD = 75° и BC = 1.

7. В равнобедренном треугольнике ABC с углом 120° при вершине A проведена биссектриса BD. В треугольник ABC вписан прямоугольник DEFH так, что сторона FH лежит на отрезке BC, а вершина E — на отрезке AB.

а) Докажите, что FH = 2DH.

б) Найдите площадь прямоугольника DEFH, если AB = 4.

8. Из вершины С прямого угла прямоугольного треугольника ABC проведена высота CH.

а) Докажите, что отношение площадей кругов, построенных на отрезках AH и BH соответственно как на диаметрах равно

б) Пусть точка O₁ — центр окружности диаметра AH, вторично пересекающей отрезок AC в точке P, а точка O₂ — центр окружности с диаметром BH, вторично пересекающей отрезок BC в точке Q. Найдите площадь четырёхугольника O₁PQO₂, если

9. Дана трапеция KLMN с основаниями KN и LM. Окружности, построенные на боковых сторонах KL и MN как на диаметрах, пересекаются в точках A и B.

а) Докажите, что средняя линия трапеции лежит на серединном перпендикуляре к отрезку AB.

б) Найдите AB, если известно, что боковые стороны трапеции равны 26 и 28, а средняя линия трапеции равна 15.

10. На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а) Докажите, что точки A, B, K и E лежат на одной окружности.

б) Найдите радиус этой окружности, если AB = 24, CH = 7.

ПРОФИЛЬ ЕГЭ математика

1. Четырёхугольник ABCD вписан в окружность. Диаметр CC₁ перпендикулярен стороне AD и пересекает её в точке M, а диаметр DD₁ перпендикулярен стороне AB и пересекает её в точке N.

а) Пусть AA₁ также диаметр окружности. Докажите, что

б) Найдите углы четырехугольника ABCD, если

2. Прямая, проходящая через вершину В, прямоугольника ABCD, перпендикулярная диагонали АС и пересекает сторону АD в точке M, равноудаленной от вершин В и D.

а) Докажите, что BM и ВD делят угол В на три равных угла.

б) Найдите расстояние от точки пересечения диагоналей прямоугольника ABCD до прямой СМ, если

3. Отрезок CH — высота прямоугольного треугольника ABC с прямым углом C. На катетах AC и BC выбраны точки M и N соответственно такие, что

a) Докажите, что треугольник MNH подобен треугольнику ABC.

б) Найдите CN, если BC = 2, AC = 4, CM = 1.

4. Хорды AD, BE и CF окружности делят друг друга на три равные части.

а) Докажите, что эти хорды равны.

б) Найдите площадь шестиугольника ABCDEF, если точки A, B, C, D, E последовательно расположены на окружности, а радиус окружности равен

5. Дана трапеция с диагоналями равными 6 и 8. Сумма оснований равна 10.

а) Докажите, что диагонали перпендикулярны.

б) Найдите высоту трапеции.

6. Две окружности касаются внутренним образом в точке A, причем меньшая окружность проходит через через центр O большей. Диаметр BC большей окружности вторично пересекает меньшую окружность в точке M, отличной от A. Лучи AO и AM вторично пересекают большую окружность в точках P и Q соответственно. Точка C лежит на дуге AQ большей окружности, не содержащей точку P.

а) Докажите, что прямые PQ и BC параллельны.

б) Известно, что sinAOC = Прямые PC и AQ пересекаются в точке K. Найдите отношение QK:KA.

7. Окружность проходит через вершины B и C треугольника ABC и пересекает AB и AC в точках C₁ и B₁ соответственно.

а) Докажите, что треугольник ABC подобен треугольнику AB₁C₁.

б) Найдите радиус данной окружности, если ∠ A = 45°, B₁C₁ = 6 и площадь треугольника AB₁C₁ в восемь раз меньше площади четырёхугольника BCB₁C₁.

8. В четырёхугольнике ABCD противоположные стороны не параллельны. Диагонали четырёхугольника ABCD пересекаются в точке O под прямым углом и образуют четыре подобных треугольника, у каждого из которых одна из вершин — точка O.

а) Докажите, что около четырёхугольника ABCD можно описать окружность.

б) Найдите радиус вписанной окружности, если AC = 10, BD = 26.

9. На катетах AC и BC прямоугольного треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M — середина гипотенузы AB, H — точка пересечения прямых CM и DK.

а) Докажите, что CMDK.

б) Найдите MH, если известно, что катеты треугольника ABC равны 30 и 40.

10. Окружность с центром О, вписанная в треугольник АВС, касается его сторон ВС, АВ и АС в точках K, L и М соответственно. Прямая КМ вторично пересекает в точке Р окружность радиуса АМ с центром А.

а) Докажите, что прямая АР параллельна прямой ВС.

б) Пусть AM = 3, CM = 2, Q — точка пересечения прямых КМ и АВ, а Т — такая точка на отрезке РQ, что Найдите QT.

🎥 Видео

№158. Через вершину В ромба ABCD проведена прямая ВМ, перпендикулярная к его плоскости. НайдитеСкачать

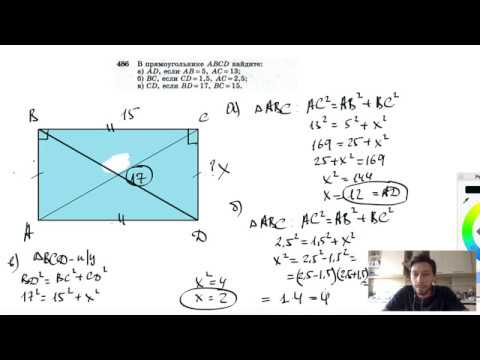
№486. В прямоугольнике ABCD найдите:Скачать

№150. Через вершину А прямоугольника ABCD проведена прямая АК, перпендикулярная к плоскостиСкачать

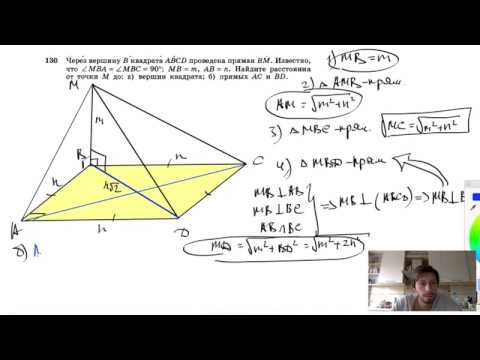
№130. Через вершину В квадрата ABCD проведена прямая ВМ. Известно, что ∠MBA = ∠MBC=90°, МВ =m, АВСкачать

№120. Через точку О пересечения диагоналей квадрата со стороной а проведена прямая ОКСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

№131. В тетраэдре ABCD точка М — середина ребра ВС, АВ = AC, DB = DC. Докажите, что плоскостьСкачать

ОГЭ бе рекламы математика 2021 задача 25 1 и 2 вариантСкачать

№374. Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке КСкачать

№152. Через вершину В квадрата ABCD проведена прямая BF, перпендикулярная к его плоскости. НайдитеСкачать

Геометрия Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точкахСкачать

№68. Точки М и N — середины ребер АВ и АС тетраэдра ABCD. Докажите, что прямая MN параллельнаСкачать

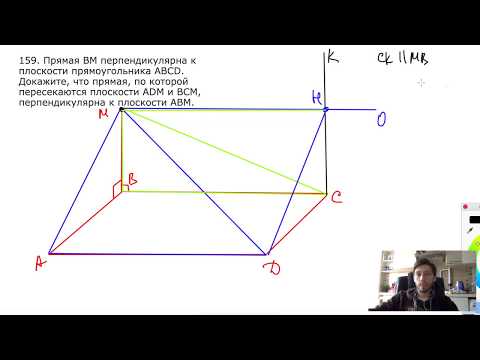
№159. Прямая ВМ перпендикулярна к плоскости прямоугольника ABCD. ДокажитеСкачать

ОГЭ 2022 Ященко 2 вариант ФИПИ школе полный разбор!Скачать

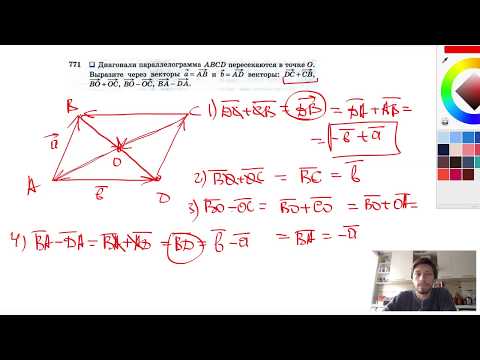
№771. В параллелограмме ABCD диагонали пересекаются в точке ОСкачать

№ 101-200 - Геометрия 9 класс МерзлякСкачать