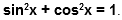Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.
Вот что мы видим на этом рисунке:
Видео:Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

А теперь подробно о тригонометрическом круге:
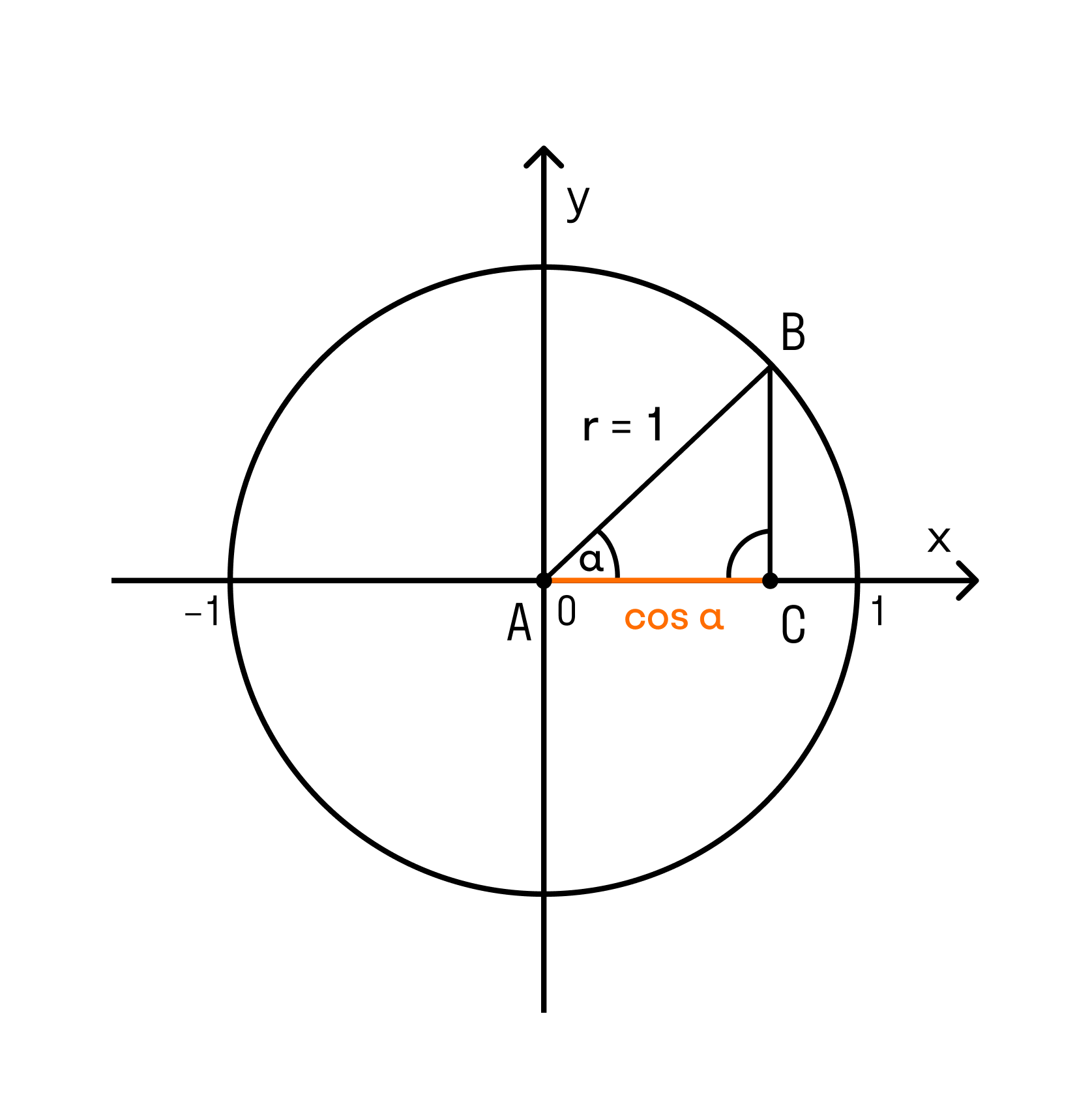
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.
Мы отсчитываем углы от положительного направления оси против часовой стрелки.
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.
Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .
Всё это легко увидеть на нашем рисунке.
Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :
Простым следствием теоремы Пифагора является основное тригонометрическое тождество:
Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).
Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.
Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.
Легко заметить, что
Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:
где — целое число. То же самое можно записать в радианах:
Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,
Видео:Отбор корней по окружностиСкачать

Единичная окружность
О чем эта статья:
10 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Видео:Как решать тригонометрические неравенства?Скачать

Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
- Если угол находится в первом квадранте, все тригонометрические функции имеют положительные значения.
- Для угла во втором квадранте все функции, за исключением sin и cos, отрицательны.
- В третьем квадранте значения всех функций, кроме tg и ctg, меньше нуля.
- В четвертом квадранте все функции, за исключением cos и sec, имеют отрицательные значения.
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
- 2π радиан = 360°
- 1 радиан = (360/2π) градусов
- 1 радиан = (180/π) градусов
- 360° = 2π радиан
- 1° = (2π/360) радиан
- 1° = (π/180) радиан
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Видео:🔴 ТРИГОНОМЕТРИЯ С НУЛЯ (Тригонометрическая Окружность на ЕГЭ 2024 по математике)Скачать

Функция y = sin x, её свойства и график
п.1. Развертка ординаты движения точки по числовой окружности в функцию от угла
При движении точки по числовой окружности её ордината является синусом соответствующего угла (см. §2 данного справочника).
Рассмотрим, как изменяется синус, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=sinx на этом отрезке.
Если мы продолжим движение по окружности для углов x > 2π, кривая продолжится вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x синусоидой .
Часть синусоиды для 0≤x≤2π называют волной синусоиды .
Часть синусоиды для 0≤x≤π называют полуволной или аркой синусоиды .
п.2. Свойства функции y=sinx
1. Область определения (xinmathbb) — множество действительных чисел.
2. Функция ограничена сверху и снизу
Область значений (yin[-1;1])
3. Функция нечётная
4. Функция периодическая с периодом 2π
5. Максимальные значения (y_=1) достигаются в точках
Минимальные значения (y_=-1) достигаются в точках
Нули функции (y_=sinx_0=0) достигаются в точках (x_0=pi k)
6. Функция возрастает на отрезках
$$ -fracpi2+2pi kleq xleqfracpi2+2pi k $$
Функция убывает на отрезках
$$ fracpi2+2pi kleq xleqfrac+2pi k $$
7. Функция непрерывна.
п.3. Примеры
Пример 1. Найдите наименьшее и наибольшее значение функции y=sinx на отрезке:
a) (left[fracpi6; fracright]) $$ y_=sinleft(fracpi6right)=frac12, y_=sinleft(fracpi2right)=1 $$ б) (left[frac; fracright]) $$ y_=sinleft(fracright)=-1, y_=sinleft(fracright)=frac12 $$
Пример 2. Решите уравнение графически:
a) (sinx=3x)
Один корень: x = 0
б) (sinx=2x-2pi)
Один корень: x = π
в) (sinx-sqrt=0)
(sinx=sqrt)
Один корень: x = π
г*) (sinx=left(x-fracpi2right)^2-frac)
(y=left(x-fracpi2right)^2-frac) – парабола ветками вверх, с осью симметрии (x_0=fracpi2) и вершиной (left(fracpi2; -fracright)) (см. §29 справочника для 8 класса)
Два корня: (x_1=0, x_2=pi)
Пример 3. Постройте в одной системе координат графики функций $$ y=sinx, y=-sinx, y=2sinx, y=sinx+2 $$
(y=-sinx) – отражение исходной функции (y=sinx) относительно оси OX. Область значений (yin[-1;1]).
(y=2sinx) – исходная функция растягивается в 2 раза по оси OY. Область значений (yin[-2;2]).
(y=sinx+2) — исходная функция поднимается вверх на 2. Область значений (yin[1;3]).
Пример 4. Постройте в одной системе координат графики функций $$ y=sinx, y=sin2x, y=sinfrac $$
Амплитуда колебаний у всех трёх функций одинакова, область значений (yin[-1;1]).
Множитель под синусом изменяет период колебаний.
(y=sin2x) — период уменьшается в 2 раза, полная волна укладывается в отрезок (0leq xleq pi).
(y=sinfrac) — период увеличивается в 2 раза, полная волна укладывается в отрезок (0leq xleq 4pi).
🎥 Видео
Решаем уравнение: 2sin²(π/2-x)+sin2x=0Скачать

How to Solve cos(x) + sin(2x) = 0 (Trigonometric Equations)Скачать

Математика| Преобразование тригонометрических выражений. Формулы и задачиСкачать

✓ Тригонометрия: с нуля и до ЕГЭ | #ТрушинLive #030 | Борис ТрушинСкачать

ТЕОРЕМА СИНУСОВ И ТЕОРЕМА КОСИНУСОВ. Тригонометрия | МатематикаСкачать

Solve the trig equation sin 2x - sin x = 0 in [0,2pi)Скачать

Синус, косинус, тангенс, котангенс за 5 МИНУТСкачать

(sin2x+2sin^2 x)/√(-cosx)=0 Задание 13 Профильный ЕГЭ по математике Исследование ОДЗСкачать

Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.Скачать

Solve: sin 2x - cos x = 0Скачать

Solve equation 2 cos x + sin 2x =0 over [0, 2pi). Double Angle FormulaСкачать

Три способа отбора корней в задании 13 ЕГЭ профильСкачать

Solving Trigonometric Equations sin2x+sinx=0, How to Solve Trigonometric EquationsСкачать

Синус, косинус, тангенс и котангенс углов от 0 до 180 градусов.Скачать
Реальный ЕГЭ-2022, профильная математика, задача 12: sin2x-2sin(-x)-cos(-x)-1=0.Скачать

Как решать тригонометрическое уравнение 3cos^2x-sinx-1=0 Замена sinx=t Уравнение с косинусом и синусСкачать