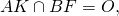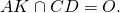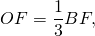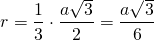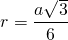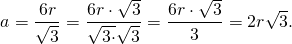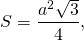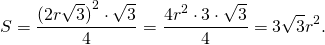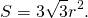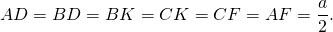Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла |
 Формулы для радиуса окружности, вписанной в треугольник Формулы для радиуса окружности, вписанной в треугольник |
 Вывод формул для радиуса окружности, вписанной в треугольник Вывод формул для радиуса окружности, вписанной в треугольник |
- Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
- Формулы для радиуса окружности, вписанной в треугольник
- Вывод формул для радиуса окружности, вписанной в треугольник
- Центр вписанной окружности является точкой пересечения его медиан
- Окружность, вписанная в правильный треугольник
- 🎬 Видео
Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Существование окружности, вписанной в треугольник. Основное свойство биссектрисы угла
Определение 1 . Биссектрисой угла называют луч, делящий угол на две равные части.
Теорема 1 (Основное свойство биссектрисы угла) . Каждая точка биссектрисы угла находится на одном и том же расстоянии от сторон угла (рис.1).
Доказательство . Рассмотрим произвольную точку D , лежащую на биссектрисе угла BAC , и опустим из точки D перпендикуляры DE и DF на стороны угла (рис.1). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны острые углы DAF и DAE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1) . Если некоторая точка находится на одном и том же расстоянии от сторон угла, то она лежит на биссектрисе угла (рис.2).
Доказательство . Рассмотрим произвольную точку D , лежащую внутри угла BAC и находящуюся на одном и том же расстоянии от сторон угла. Опустим из точки D перпендикуляры DE и DF на стороны угла (рис.2). Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE , а гипотенуза AD – общая. Следовательно,
что и требовалось доказать.
Определение 2 . Окружность называют окружностью, вписанной в угол , если она касается касается сторон этого угла.
Теорема 3 . Если окружность вписана в угол, то расстояния от вершины угла до точек касания окружности со сторонами угла равны.
Доказательство . Пусть точка D – центр окружности, вписанной в угол BAC , а точки E и F – точки касания окружности со сторонами угла (рис.3).
Прямоугольные треугольники ADF и ADE равны, поскольку у них равны катеты DF и DE (как радиусы окружности радиусы окружности ), а гипотенуза AD – общая. Следовательно
что и требовалось доказать.
Замечание . Теорему 3 можно сформулировать и по-другому: отрезки касательных касательных , проведенных к окружности из одной точки, равны.
Определение 3 . Биссектрисой треугольника называют отрезок, являющийся частью биссектрисы угла треугольника, и соединяющий вершину треугольника с точкой на противоположной стороне.
Теорема 4 . В любом треугольнике все три биссектрисы пересекаются в одной точке.
Доказательство . Рассмотрим две биссектрисы, проведённые из вершин A и C треугольника ABC , и обозначим точку их пересечения буквой O (рис. 4).
Опустим из точки O перпендикуляры OD , OE и OF на стороны треугольника. Поскольку точка O лежит на биссектрисе угла BAC , то в силу теоремы 1 справедливо равенство:
Поскольку точка O лежит на биссектрисе угла ACB , то в силу теоремы 1 справедливо равенство:
Следовательно, справедливо равенство:
откуда с помощью теоремы 2 заключаем, что точка O лежит на биссектрисе угла ABC . Таким образом, все три биссектрисы треугольника проходят через одну и ту же точку, что и требовалось доказать
Определение 4 . Окружностью, вписанной в треугольник , называют окружность, которая касается всех сторон треугольника (рис.5). В этом случае треугольник называют треугольником, описанным около окружности .
Следствие . В любой треугольник можно вписать окружность, причем только одну. Центром вписанной в треугольник окружности является точка, в которой пересекаются все биссектрисы треугольника.
Видео:Медианы | Свойства медиан | Точка пересечения медиан на прямой ЭйлераСкачать

Формулы для радиуса окружности, вписанной в треугольник
Формулы, позволяющие найти радиус вписанной в треугольник окружности , удобно представить в виде следующей таблицы.
| Фигура | Рисунок | Формула | Обозначения | |||||||||||||||||||
| Произвольный треугольник |  | |||||||||||||||||||||
| Равнобедренный треугольник |  | |||||||||||||||||||||
| Равносторонний треугольник |  | |||||||||||||||||||||
| Прямоугольный треугольник |  | |||||||||||||||||||||
| Произвольный треугольник | ||
 | ||
| Равнобедренный треугольник | ||
 | ||
| Равносторонний треугольник | ||
 | ||
| Прямоугольный треугольник | ||
 | ||
| Произвольный треугольник |
 |
где
a, b, c – стороны треугольника,
S –площадь,
r – радиус вписанной окружности,
p – полупериметр

где
a, b, c – стороны треугольника,
r – радиус вписанной окружности,
p – полупериметр


где
a – сторона равностороннего треугольника,
r – радиус вписанной окружности

Видео:ГЕОМЕТРИЯ 8 класс: 4 замечательные точкиСкачать

Вывод формул для радиуса окружности, вписанной в треугольник
Теорема 5 . Для произвольного треугольника справедливо равенство
где a, b, c – стороны треугольника, r – радиус вписанной окружности, 
с помощью формулы Герона получаем:
что и требовалось.
Теорема 6 . Для равнобедренного треугольника справедливо равенство
где a – боковая сторона равнобедренного треугольника, b – основание, r – радиус вписанной окружности (рис. 7).
то, в случае равнобедренного треугольника, когда
что и требовалось.
Теорема 7 . Для равностороннего треугольника справедливо равенство
где a – сторона равностороннего треугольника, r – радиус вписанной окружности (рис. 8).
то, в случае равностороннего треугольника, когда
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в равносторонний треугольник, непосредственно, т.е. без использования общих формул для радиусов окружностей, вписанных в произвольный треугольник или в равнобедренный треугольник.
Теорема 8 . Для прямоугольного треугольника справедливо равенство
Доказательство . Рассмотрим рисунок 9.
Поскольку четырёхугольник CDOF является прямоугольником прямоугольником , у которого соседние стороны DO и OF равны, то этот прямоугольник – квадрат квадрат . Следовательно,
В силу теоремы 3 справедливы равенства
Следовательно, принимая также во внимание теорему Пифагора, получаем
что и требовалось.
Замечание . Рекомендуем читателю вывести в качестве упражнения формулу для радиуса окружности, вписанной в прямоугольный треугольник, с помощью общей формулы для радиуса окружности, вписанной в произвольный треугольник.
Видео:Точка пересечения медиан.Скачать

Центр вписанной окружности является точкой пересечения его медиан
Какие из следующих утверждений верны?
1) Около всякого треугольника можно описать не более одной окружности.
2) В любой треугольник можно вписать не менее одной окружности.
3) Центром окружности, описанной около треугольника, является точка пересечения биссектрис.
4) Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.
Если утверждений несколько, запишите их номера в порядке возрастания.
Проверим каждое из утверждений.
1) «Около всякого треугольника можно описать не более одной окружности.» — верно, oколо треугольника можно описать окружность, притом только одну.
2) «В любой треугольник можно вписать не менее одной окружности.» — верно, в любой треугольник можно вписать окружность.
3) «Центром окружности, описанной около треугольника, является точка пересечения биссектрис.» — неверно, центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров треугольника.
4) «Центром окружности, вписанной в треугольник, является точка пересечения серединных перпендикуляров к его сторонам.» — неверно, центром вписанной в треугольник окружности является точка пересечения биссектрис треугольника.
Выражение «не более одной» означает, что окружностей не может быть больше одной. Выражение «не менее одной» означает, что окружностей не может быть меньше одной. В частности, «ровно одна окружность» удовлетворяет как условию «не более одной», так и условию «не менее одной».
Утверждение «В любой треугольник можно вписать не менее одной окружности» можно сформулировать так: «В любой треугольник можно вписать хотя бы одну окружность». Если бы это утверждение было неверным, это означало бы, что существуют треугольники, в которые нельзя вписать хотя бы одну окружность, но таких треугольников не существует, поэтому утверждение является верным.
Видео:Вписанные и описанные окружности. Вебинар | МатематикаСкачать

Окружность, вписанная в правильный треугольник
Окружность, вписанная в правильный треугольник, помимо свойств вписанной в произвольный треугольник окружности, обладает своими собственными свойствами.
1) Центр вписанной в треугольник окружности — точка пересечения его биссектрис.
Поскольку в равностороннем треугольнике биссектрисы, медианы и высоты совпадают, то центр вписанной в правильный треугольник окружности является точкой пересечения не только его биссектрис, но также медиан и высот.

точка O — центр вписанной окружности.
AK, BF и CD — биссектрисы, медианы и высоты треугольника ABC.
2) Расстояние от центра вписанной окружности до точки касания её со стороной треугольника равно радиусу. Так как центр вписанной в правильный треугольник окружности лежит на пересечении его медиан, а медианы треугольника в точке пересечения делятся в отношении 2:1, считая от вершины, то радиус вписанной в равносторонний треугольник окружности равен одной третьей длины медианы:
Таким образом, формула для радиуса вписанной в правильный треугольник окружности
Обратно, сторона равностороннего треугольника через радиус вписанной окружности:
3) Так как формула для нахождения площади равностороннего треугольника через сторону
можем найти площадь через r:
Таким образом, формула площади правильного треугольника через радиус вписанной окружности —
3) Все отрезки, на которые стороны равностороннего треугольника делятся точками касания вписанной окружности, равны половине его стороны:
4) Центр вписанной в правильный треугольник окружности является также центром описанной около него окружности.
5) Радиус вписанной в равносторонний треугольник окружности в два раза меньше радиуса описанной окружности:
🎬 Видео
Вписанная и описанная окружность - от bezbotvyСкачать

Центр вписанной окружности #ShortsСкачать

Центром вписанной в треугольник окружности ... | ОГЭ 2017 | ЗАДАНИЕ 13 | ШКОЛА ПИФАГОРАСкачать

Вписанная окружность | Геометрия 7-9 класс #74 | ИнфоурокСкачать

#207. Окружность девяти точек | лемма о трезубце | ортотреугольник | прямая ЭйлераСкачать

Задание 16 ЕГЭ по математикеСкачать

Геометрия 8 класс (Урок№32 - Вписанная окружность.)Скачать

Замечательные точки треугольника | Ботай со мной #030 | Борис Трушин ||Скачать

Стереометрия 10 класс. Часть 1 | МатематикаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Точка O центр окружности описанной около остроугольного треугольникаСкачать

Пересечение биссектрис треугольника в одной точке, Геометрия 7 классСкачать

Точка пересечения биссектрис, медиан, высот, серединных перпендикуляровСкачать

Окружность, вписанная в треугольник. Как найти центр и радиус. Геометрия 7-8 классСкачать

#31. Регион ВсОШ 2023, 11.5Скачать