Вписанная окружность в угол 120

Вписанная окружность — это окружность, которая вписана
в геометрическую фигуру и касается всех его сторон.

Окружность, точно можно вписать в такие геометрические фигуры, как:

• Треугольник
• Выпуклый, правильный многоугольник
• Квадрат
• Равнобедренная трапеция
• Ромб

В четырехугольник, можно вписать окружность,
только при условии, что суммы длин
противоположных сторон равны.

Во все вышеперечисленные фигуры
окружность, может быть вписана, только один раз.

Окружность невозможно вписать в прямоугольник
и параллелограмм, так как окружность не будет
соприкасаться со всеми сторонам этих фигур.

Геометрические фигуры, в которые вписана окружность,
называются описанными около окружности.

Описанный треугольник — это треугольник, который описан
около окружности и все три его стороны соприкасаются с окружностью.

Описанный четырехугольник — это четырехугольник, который описан
около окружности и все четыре его стороны соприкасаются с окружностью.

Свойства вписанной окружности

В треугольник

1. В любой треугольник может быть вписана окружность, причем только один раз.
2. Центр вписанной окружности — точка пересечения биссектрис треугольника.
3. Вписанная окружность касается всех сторон треугольника.
4. Площадь треугольника, в который вписана окружность, можно рассчитать по такой формуле:

[ S = frac(a+b+c) cdot r = pr ]

p — полупериметр четырехугольника.
r — радиус вписанной окружности четырехугольника.

Примеры вписанной окружности

• Треугольник
  
• Четырехугольник
  
• Многоугольник
  

Примеры описанного четырехугольника:
равнобедренная трапеция, ромб, квадрат.

Примеры описанного треугольника:
равносторонний, равнобедренный,
прямоугольный треугольники.

Верные и неверные утверждения

1. Радиус вписанной окружности в треугольник и радиус вписанной
   в четырехугольник вычисляется по одной и той же формуле. Верное утверждение.
2. Любой параллелограмм можно вписать в окружность. Неверное утверждение.
3. В любой четырехугольник можно вписать окружность. Неверное утверждение.
4. В любой ромб можно вписать окружность. Верное утверждение.
5. Центр вписанной окружности треугольника это точка пересечения биссектрис. Верное утверждение.
6. Окружность вписанная в треугольник касается всех его сторон. Верное утверждение.
7. Угол вписанный в окружность равен соответствующему центральному
   углу опирающемуся на ту же дугу. Неверное утверждение.
8. Радиус вписанной окружности в прямоугольный треугольник равен
   половине разности суммы катетов и гипотенузы. Верное утверждение.
9. Вписанные углы опирающиеся на одну и ту же хорду окружности равны. Неверное утверждение.
10. Вписанная окружность в треугольник имеет в общем
    три общие точки со всеми сторонами треугольника. Верное утверждение.

Окружность вписанная в угол

Окружность вписанная в угол — это окружность, которая
лежит внутри этого угла и касается его сторон.

Центр окружности, которая вписана в угол,
расположен на биссектрисе этого угла.

К центру окружности вписанной в угол, можно провести,
в общей сложности два перпендикуляра со смежных сторон.

Длина диаметра, радиуса, хорды, дуги вписанной окружности
измеряется в км, м, см, мм и других единицах измерения.

Видео:Геометрия Точка O центр окружности вписанной в треугольник ABC BC = a AC = b угол AOB = 120 НайдитеСкачать

В угол 120 градусов вписана окружность радиуса 8 см?

Геометрия | 5 — 9 классы

В угол 120 градусов вписана окружность радиуса 8 см.

Найдите расстояние между точками касания окружности со сторонами угла.

Рассмотрим получившийся четырёхуголльник.

Угол, в который вписана окружность, равен 120.

Касательные перпендикулярны радиусам окружности = &gt ;

углы между ними равны 90.

Центральный угол равен 360 — 120 — 180 = 60.

Он равнобедренный, т.

К. две его стороны — радиусы.

Центральный угол равен 60, = &gt ; треугольник — равносторонний.

= &gt ; искомый отрезок равен 8.

Видео:Вписанная и описанная окружность - от bezbotvyСкачать

Две окружности, каждая из которых вписана в острый угол 60 градусов, касаются друг друга внешним образом?

Две окружности, каждая из которых вписана в острый угол 60 градусов, касаются друг друга внешним образом.

Найдите расстояние от точки касания окружностей до стороны угла, если радиус большей окружности равен 23.

Видео:Задача 6 №27862 ЕГЭ по математике. Урок 105Скачать

Радиус окружности, вписанной в равнобочную трапецию, равен 3, а площадь трапеции равна 108?

Радиус окружности, вписанной в равнобочную трапецию, равен 3, а площадь трапеции равна 108.

Найдите расстояние между точками касания окружности боковых сторон трапеции.

Видео:Окружность вписанная в треугольник и описанная около треугольника.Скачать

Две окружности вписанные в угол 60 градусов касаются друг друга внешним образом найти расстояние от точки касания окружности до стороны угла?

Две окружности вписанные в угол 60 градусов касаются друг друга внешним образом найти расстояние от точки касания окружности до стороны угла.

Радиус большей окружности 23.

Видео:ЕГЭ Математика Задание 6#27862Скачать

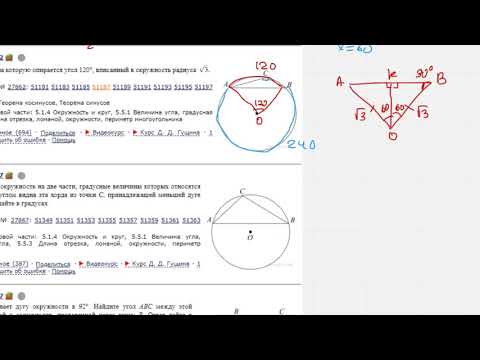
В острый угол вписана окружность радиуса 1, 3?

В острый угол вписана окружность радиуса 1, 3.

Найти расстояние от вершины угла до точки касания, если расстояние между точками касания равно 2, 4.

Видео:Всё про углы в окружности. Геометрия | МатематикаСкачать

В ТРЕУГОЛИНИКЕ 30, 70, 80 ГРАДУСОВ ВПИСАНА ОКРУЖНОСТЬ?

В ТРЕУГОЛИНИКЕ 30, 70, 80 ГРАДУСОВ ВПИСАНА ОКРУЖНОСТЬ.

НАЙДИТЕ УГЛЫ ТРЕУГОЛНИКА, ВЕРШИНАМИ КОТОРОГО ЯВЛЯЮТСЯ ТОЧКИ КАСАНИЯ ВПИСАННОЙ ОКРУЖНОСТИ СО СТОРОНАМИ ДАННОГО ТРЕУГОЛЬНИКА.

Видео:Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса кореньСкачать

В угол АВС, равный 76 градусам, вписана окружность с центром О, имеющая со сторонами угла АСВ точки касания А и В?

В угол АВС, равный 76 градусам, вписана окружность с центром О, имеющая со сторонами угла АСВ точки касания А и В.

Найдите величину угла АОВ.

Ответ дайте в градусах.

Видео:Задача 6 №27900 ЕГЭ по математике. Урок 128Скачать

В угол равный 120 град вписана окружность радиуса 8 см?

В угол равный 120 град вписана окружность радиуса 8 см.

Найдите расстояние между точками касания окружности со сторонами угла.

Видео:Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса через тСкачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.

Найдите угол АОВ.

Видео:8 класс, 38 урок, Вписанная окружностьСкачать

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности?

В угол C величиной 72 градуса вписана окружность, которая касается сторон угла в точках А и В, Где О — центр окружности.

Найдите угол АОВ.

Видео:Построение угла 120 градусов с помощью циркуля и линейки.Скачать

В тругольнике авс угол а = 60 градусов?

В тругольнике авс угол а = 60 градусов.

Радиус окружности вписанный в этот треугольник равен 1 найти расстояние от точки касания окружности и прямой АС до вершины А.

На этой странице сайта, в категории Геометрия размещен ответ на вопрос В угол 120 градусов вписана окружность радиуса 8 см?. По уровню сложности вопрос рассчитан на учащихся 5 — 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

В треугольнике АВО ∠В = ∠А = 30⇒∠О = 180 — 60 = 120°⇒ Углы между диагоналями 120°и 60°.

В р. б. Треугольнике углы при основании равны, значит.

Тангенс угла АОБ = БА / ОА = 8 / 8 = 1.

AM + PO + ML — PL = (AM + ML) + (PO — PL) = AL + OL.

Рассмотрим треуг — ки ANC и AMC : У них общее основание — АС, и равные углы при основании, т. К. углы при основании в равнобедренном треугольнике равны. Имеем : угол NAC = углу MCA по условию задачи, но углы BAC = BCA, то есть равны и другие части ..

Формула а + б разделить на 2 и умножить на высоту.

180 — 30 = 150 150 : 2 = 75 ответ : 75 ; 105.

1) N = K = 45° + 65° = 110° M = P = 360° — (N + K) = 360° — 220° / 2 = 140° / 2 = 70° 2) плохо видно цифру, поэтому напишу как вижу– 35° угол MKF = углу MFK = 35° F = K = 35°×2 = 70° M = E = 360° — (F + K) = 360° — 140° / 2 = 220° / 2 = 110° 3) B = C..

Вот решение задание которое нужно.

В треугольнике 180 градусов : 180 — (80 + 56) = 44.

Видео:Решение задач на тему центральные и вписанные углы.Скачать

Окружность: вписанная в многоугольник или угол

Определения

Окружность (S) вписана в угол (alpha) , если (S) касается сторон угла (alpha) .

Окружность (S) вписана в многоугольник (P) , если (S) касается всех сторон (P) .

В этом случае многоугольник (P) называется описанным около окружности.

Теорема

Центр вписанной в угол окружности лежит на его биссектрисе.

Доказательство

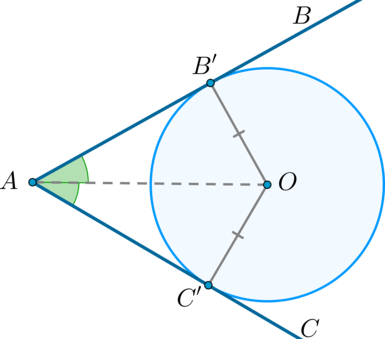
Пусть (O) – центр некоторой окружности, вписанной в угол (BAC) . Пусть (B’) – точка касания окружности и (AB) , а (C’) – точка касания окружности и (AC) , тогда (OB’) и (OC’) – радиусы, проведённые в точки касания, следовательно, (OC’perp AC) , (OB’perp AB) , (OC’ = OB’) .

Значит, треугольники (AC’O) и (AB’O) – прямоугольные треугольники, у которых равны катеты и общая гипотенуза, следовательно, они равны, откуда (angle CAO = angle BAO) , что и требовалось доказать.

Теорема

В любой треугольник можно вписать единственную окружность, причём центр этой вписанной окружности есть точка пересечения биссектрис треугольника.

Доказательство

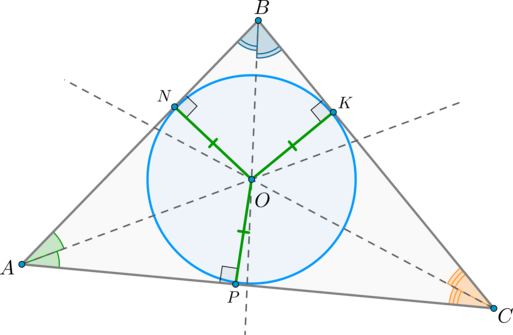
Проведем биссектрисы углов (angle A) и (angle B) . Пусть они пересеклись в точке (O) .

Т.к. (O) лежит на биссектрисе (angle A) , то расстояния от точки (O) до сторон угла равны: (ON=OP) .

Т.к. (O) также лежит на биссектрисе (angle B) , то (ON=OK) . Таким образом, (OP=OK) , следовательно, точка (O) равноудалена от сторон угла (angle C) , следовательно, лежит на его биссектрисе, т.е. (CO) – биссектриса (angle C) .

Таким образом, точки (N, K, P) равноудалены от точки (O) , то есть лежат на одной окружности. По определению это и есть вписанная в треугольник окружность.

Данная окружность единственна, т.к. если предположить, что существует другая вписанная в (triangle ABC) окружность, то она будет иметь тот же центр и тот же радиус, то есть будет совпадать с первой окружностью.

Таким образом, попутно была доказана следующая теорема:

Следствие

Биссектрисы треугольника пересекаются в одной точке.

Теорема о площади описанного треугольника

Если (a,b,c) – стороны треугольника, а (r) – радиус вписанной в него окружности, то площадь треугольника [S_=pcdot r] где (p=dfrac2) – полупериметр треугольника.

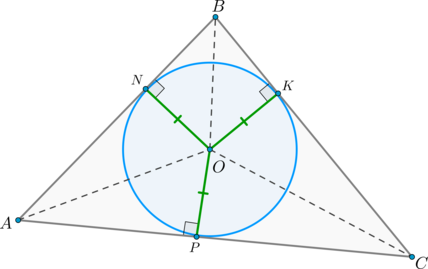
Доказательство

Но (ON=OK=OP=r) – радиусы вписанной окружности, следовательно,

Следствие

Если в многоугольник вписана окружность и (r) – ее радиус, то площадь многоугольника равна произведению полупериметра многоугольника на (r) : [S_<text>=pcdot r]

Теорема

В выпуклый четырёхугольник можно вписать окружность тогда и только тогда, когда суммы его противоположных сторон равны.

Доказательство

Необходимость. Докажем, что если в (ABCD) вписана окружность, то (AB+CD=BC+AD) .

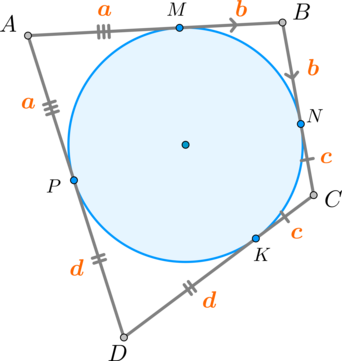
Пусть (M,N,K,P) – точки касания окружности и сторон четырехугольника. Тогда (AM, AP) – отрезки касательных к окружности, проведенные из одной точки, следовательно, (AM=AP=a) . Аналогично, (BM=BN=b, CN=CK=c, DK=DP=d) .

Достаточность. Докажем, что если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность.

Проведем биссектрисы углов (angle A) и (angle B) , пусть они пересекутся в точке (O) . Тогда точка (O) равноудалена от сторон этих углов, то есть от (AB, BC, AD) . Впишем окружность в (angle A) и (angle B) с центром в точке (O) . Докажем, что эта окружность будет касаться и стороны (CD) .

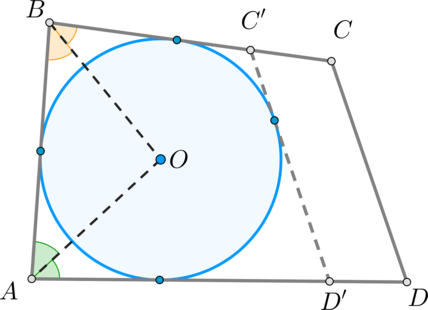
Предположим, что это не так. Тогда (CD) либо является секущей, либо не имеет общих точек с окружностью. Рассмотрим второй случай (первый будет доказываться аналогично).

Проведем касательную прямую (C’D’ parallel CD) (как показано на рисунке). Тогда (ABC’D’) – описанный четырехугольник, следовательно, (AB+C’D’=BC’+AD’) .

Т.к. (BC’=BC-CC’, AD’=AD-DD’) , то:

[AB+C’D’=BC-CC’+AD-DD’ Rightarrow C’D’+CC’+DD’=BC+AD-AB=CD]

Получили, что в четырехугольнике (C’CDD’) сумма трех сторон равна четвертой, что невозможно*. Следовательно, предположение ошибочно, значит, (CD) касается окружности.

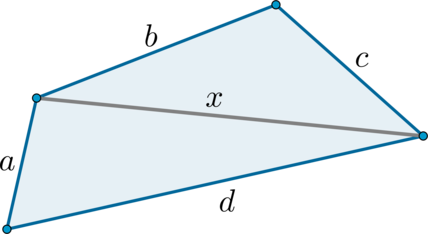
Замечание*. Докажем, что в выпуклом четырехугольнике не может сторона равняться сумме трех других.

Т.к. в любом треугольнике сумма двух сторон всегда больше третьей, то (a+x>d) и (b+c>x) . Складывая данные неравенства, получим: (a+x+b+c>d+x Rightarrow a+b+c>d) . Следовательно, сумма любых трех сторон всегда больше четвертой стороны.

Теоремы

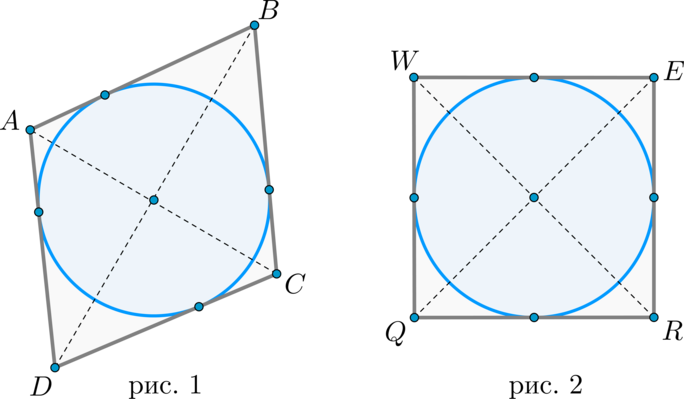
1. Если в параллелограмм вписана окружность, то он – ромб (рис. 1).

2. Если в прямоугольник вписана окружность, то он – квадрат (рис. 2).

Верны и обратные утверждения: в любой ромб и квадрат можно вписать окружность, и притом только одну.

Доказательство

1) Рассмотрим параллелограмм (ABCD) , в который вписана окружность. Тогда (AB+CD=BC+AD) . Но в параллелограмме противоположные стороны равны, т.е. (AB=CD, BC=AD) . Следовательно, (2AB=2BC) , а значит, (AB=BC=CD=AD) , т.е. это ромб.

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей ромба.

2) Рассмотрим прямоугольник (QWER) . Т.к. прямоугольник является параллелограммом, то согласно первому пункту (QW=WE=ER=RQ) , т.е. это ромб. Но т.к. все углы у него прямые, то это квадрат.

Обратное утверждение очевидно, причем центр этой окружности лежит на пересечении диагоналей квадрата.

🔥 Видео

Как начертить три линии под 120 градусов и шестиугольникСкачать

Углы, вписанные в окружность. 9 класс.Скачать

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

Четырехугольники, вписанные в окружность. 9 класс.Скачать

Нахождение диаметра описанной окружностиСкачать

Математика | 5 ЗАДАЧ НА ТЕМУ ОКРУЖНОСТИ. Касательная к окружности задачиСкачать

ВПИСАННАЯ ОКРУЖНОСТЬ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать