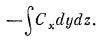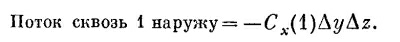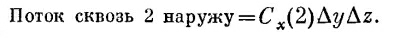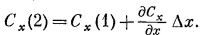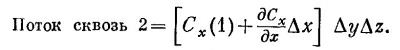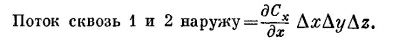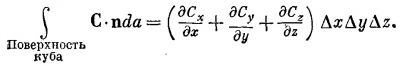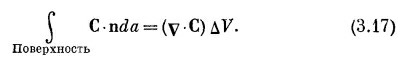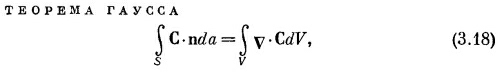| Теорема Гаусса для вектора магнитной индукции |   |
Как было показано выше, в природе нет магнитных зарядов. В 1931 г. П. Дирак высказал предположение о существовании обособленных магнитных зарядов, названных впоследствии монополи Дирака. Однако до сих пор они не найдены. Это приводит к тому, что линии вектора В соответствии с вышеизложенным, можно сделать заключение, что поток вектора Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие:
Это теорема Гаусса для Этот результат является математическим выражением того, что в природе нет магнитных зарядов – источников магнитного поля, на которых начинались и заканчивались бы линии магнитной индукции. Заменив поверхностный интеграл в (1.7.1) объемным, получим:
где Это условие должно выполняться для любого произвольного объема V, а это, в свою очередь, возможно, если подынтегральная функция в каждой точке поля равна нулю. Таким образом, магнитное поле обладает тем свойством, что его дивергенция всюду равна нулю:
В этом его отличие от электростатического поля, которое является потенциальным и может быть выражено скалярным потенциалом φ, магнитное поле – вихревое, или соленоидальное (см. рис. 1.3 и 1.8). Компьютерная модель магнитного поля Земли, подтверждающая вихревой характер, изображена на рис. 1.9. На рисунке 1.10 показаны магнитное поле постоянного магнита. Линии магнитной индукции замыкаются в окружающем пространстве. Содержание Видео:Билет №16 "Теорема о циркуляции и теорема Гаусса для магнитного поля"Скачать  Поток из куба; теорема Гаусса
Так как куб считается малым, этот интеграл можно заменить значением Сх в центре грани [эту точку мы обозначили (1)], умноженным на площадь грани ΔyΔz:
Подобным же образом поток наружу через грань 2 равен
Величины Сх(1) и Сх(2), вообще говоря, слегка отличаются. Если Δx достаточно мало, то можно написать
Существуют, конечно, и другие члены, но в них входит (Δx) 2 и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен
Складывая потоки через грани 1 и 2, получаем
Производную нужно вычислять в центре грани 1, т. е. в точке [х, y + (Δy/2), z+(Δz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z). Повторяя те же рассуждения с каждой парой граней, мы получаем
А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что
Сумма производных в скобках как раз есть v·С, a ΔxΔyΔz=ΔV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба
Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р. Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.
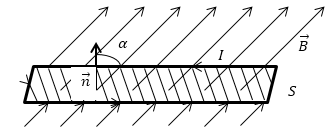
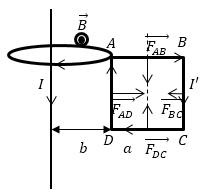
где S — произвольная замкнутая поверхность, V — объем внутри нее. Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать  Поток вектора магнитной индукции (магнитный поток)Вы будете перенаправлены на Автор24 Видео:Индукция магнитного поля | Физика 9 класс #37 | ИнфоурокСкачать  ОпределениеПотоком вектора магнитной индукции (магнитным потоком) (Ф) через площадку S называют скалярную величину равную: где $alpha $ угол между $overrightarrow$ и $overrightarrow$, $overrightarrow$ — нормаль к площадке S. Ф равен количеству линий магнитной индукции, которые пересекают площадку S (рис.1). Поток магнитной индукции может быть положительным и отрицательным. Знак потока зависит от выбора положительного направлении нормали к площадке S. Обычно, положительное направление нормали связывают с направлением обхода контура током. За положительное направление нормали принимают поступательное перемещение правого винта, при вращении его по току. В том случае, если магнитное поле неоднородно, S не является плоской, то поверхность можно разбить на элементарные площадки dS, которые рассматриваются как плоские, а поле на этой площадке можно считать однородным. В таком случае магнитный поток (dФ) можно через такую поверхность определить как: Тогда полный поток через поверхность S находится как: Основная единица измерения магнитного потока в системе СИ — вебер (Вб). $1 Вб=frac$. Видео:Электромагнитная индукция. Магнитный поток. Правило Ленца | Физика 11 класс #4 | ИнфоурокСкачать  Связь магнитного потока и работы сил магнитного поляЭлементарную работу ($delta A$), которую совершают силы магнитного поля можно выразить через элементарное изменение потока вектора магнитной индукции (dФ): [delta A=IdФ left(4right).] В том случае, когда проводник с током совершил конечное перемещение, а сила тока постоянна, то работа сил поля равна: где $Ф_1$ — поток через контур в начале перемещения, $Ф_2$ — поток через контур в конце перемещения. Видео:Теорема о циркуляции вектора магнитной индукции. Магнитный поток.Скачать  Теорема Гаусса для магнитного поляСуммарный магнитный поток через замкнутую поверхность S равен нулю: Уравнение (6) справедливо для любых магнитных полей. Это уравнение аналог теоремы Остроградского — Гаусса в электростатике (в вакууме): Уравнение (6) означает, что источником магнитного поля являются не магнитные заряды (их в природе не существует), а электрические токи. Данную теорему мы подробно рассматривали в разделе «Отсутствие в природе магнитных зарядов». Задание: Недалеко от бесконечно длинного прямого проводника с током I находится квадратная рамка, по которой течет ток с силой $I’$. Сторона рамки равна $а$. Рамка лежит в плоскости с проводом (рис.2). Расстояние от ближайшей стороны рамки до проводника равно b. Найдите работу магнитной силы при удалении рамки из поля. Считать токи постоянными. Индукция магнитного поля длинного проводника с током в части, где расположена квадратная рамка, направлена на нас. При решении этой задачи необходимо помнить, что рамка с током находится в неоднородном поле, магнитная индукция убывает при удалении от провода. В качестве основы для решения задачи используем формулу связи потока и работы: $I’$- сила тока в рамке, $Ф_1$- поток через квадратную рамку, когда расстояние от ее стороны, ближайшей к проводу равна $b$. $Ф_2=0$, так как в конечном положении рамка вне магнитного поля по условию. Следовательно, формула (1.1) запишется как: Выберем направление нормали ($overrightarrow$) к квадратному контуру от нас (по правилу правого винта). Тогда для всех элементов поверхности, которая ограничена контуром квадратной рамки угол между нормалью $overrightarrow$ и вектором $overrightarrow$ равен $pi $. Тогда формула для потока через поверхность рамки на расстоянии x от провода имеет вид: где индукция магнитного поля бесконечно длинного проводника с током силы I равна: Следовательно, весь поток из (1.3) найдем как: Подставим формулу (1.5) в выражение (1.2) найдем искомую работу: 🎥 ВидеоПоток вектора магнитной индукцииСкачать  Урок 222. Поток вектора напряженности электрического поляСкачать  ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ сила Ампера правило левой рукиСкачать  Электромагнетизм Пр3.3. Теорема Гаусса. Поле плоскости. Поток через грань кубаСкачать  Билет №02 "Теорема Гаусса"Скачать  Электромагнитная индукция. Простыми словамиСкачать  Урок 281. Электромагнитная индукция. Магнитный поток. Правило ЛенцаСкачать  53. Теорема о циркуляции вектора индукцииСкачать  Физика 11 класс (Урок№5 - Электромагнитная индукция.)Скачать  Урок 270. Магнитное поле и его характеристикиСкачать  Магнитное поле соленоидаСкачать  Галилео. Эксперимент. Электромагнитная индукцияСкачать  Урок 271. Модуль вектора магнитной индукции. Закон АмпераСкачать  Физика 9 класс (Урок№19 - Индукция магнитного поля.)Скачать  Электромагнитная индукция. ЕГЭ Физика. Николай НьютонСкачать  |

 не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности:
не имеют ни начала, ни конца. Мы знаем, что поток любого вектора через поверхность равен разности числа линий, начинающихся у поверхности, и числа линий, оканчивающихся внутри поверхности: .
. ,
, (в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.
(в интегральной форме): поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. ,
, – оператор Лапласа.
– оператор Лапласа. или
или 



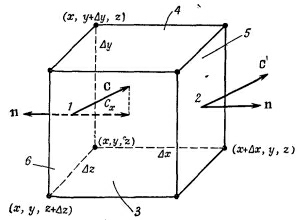 Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен
Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен