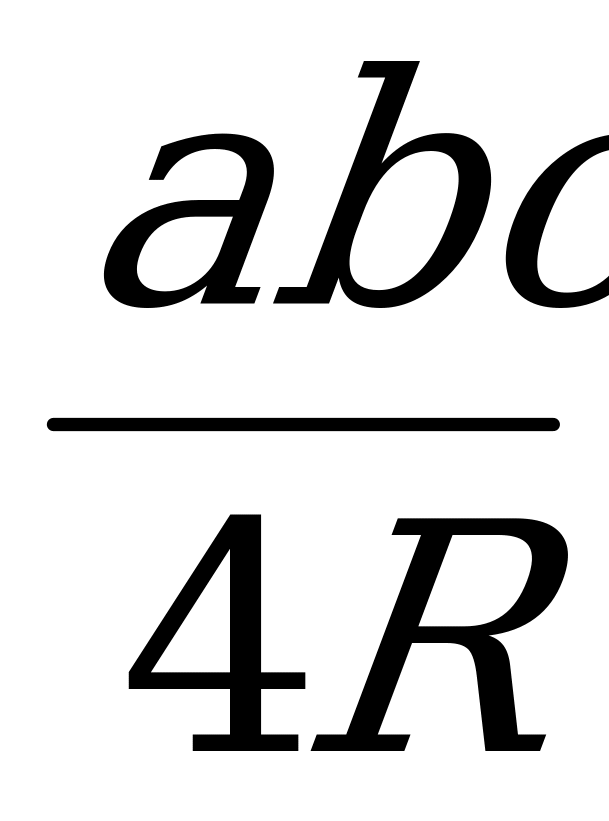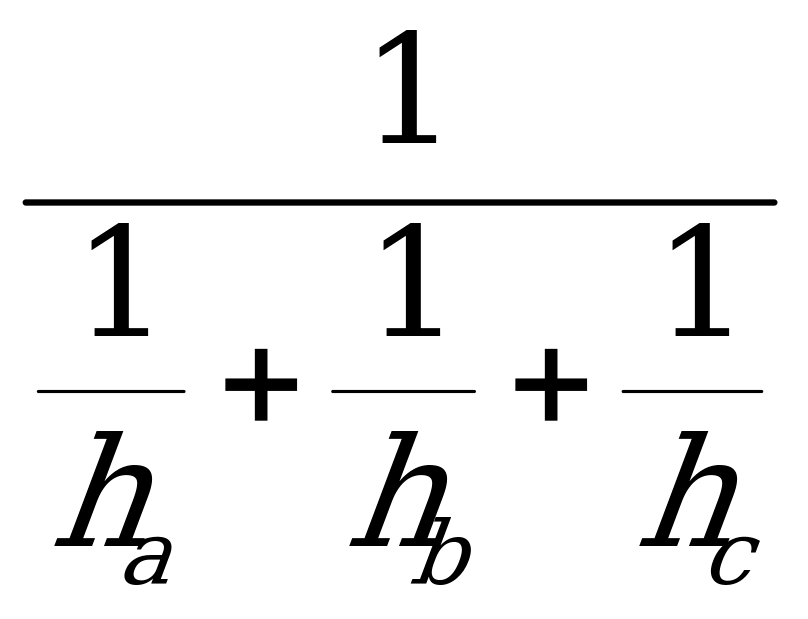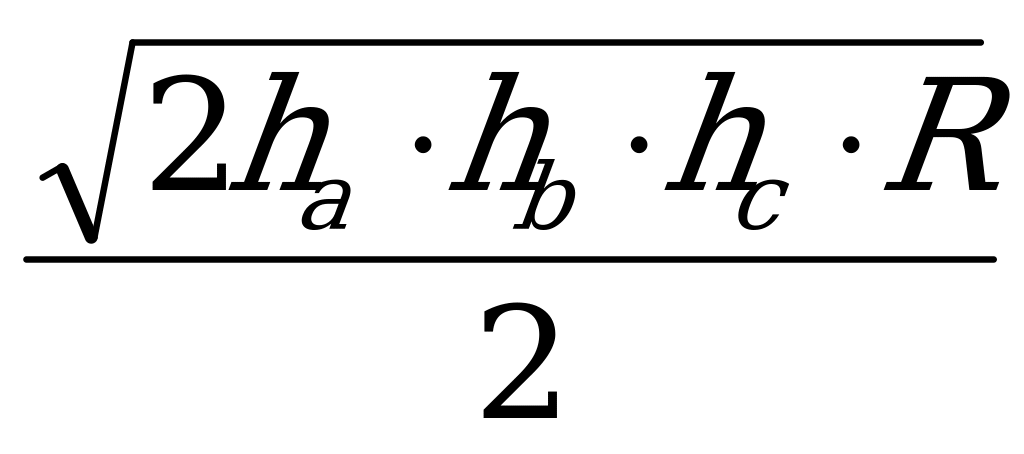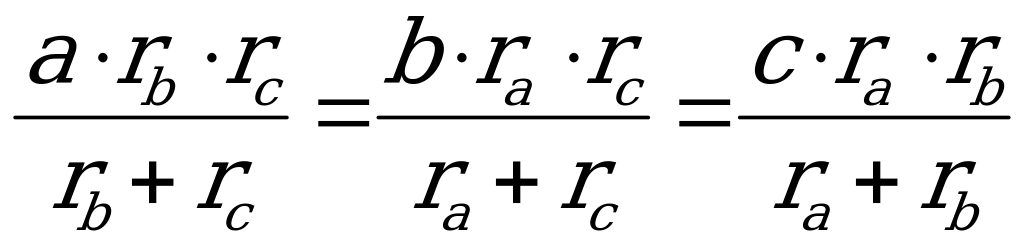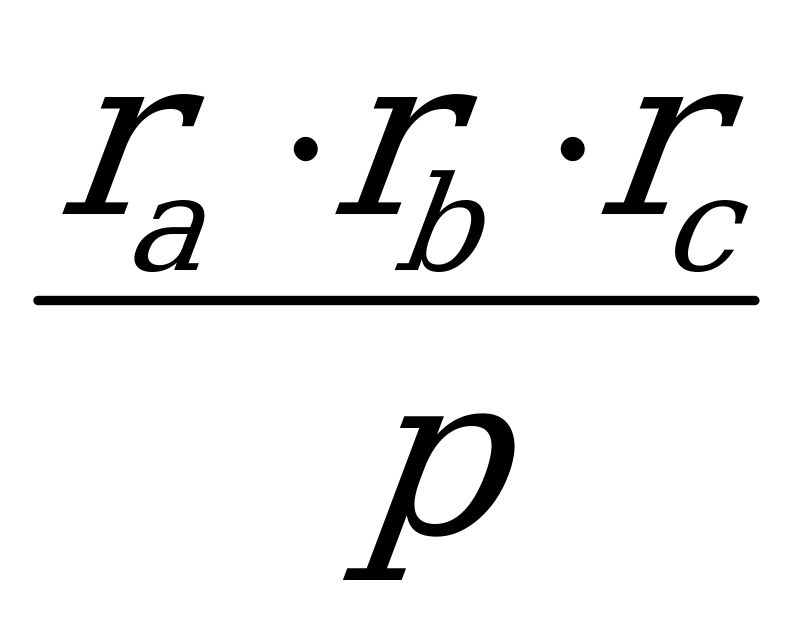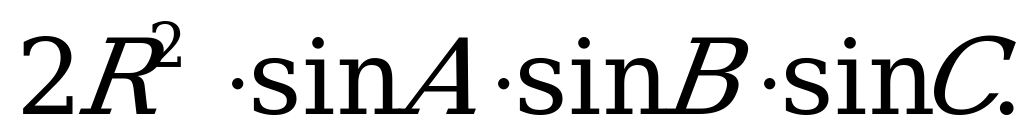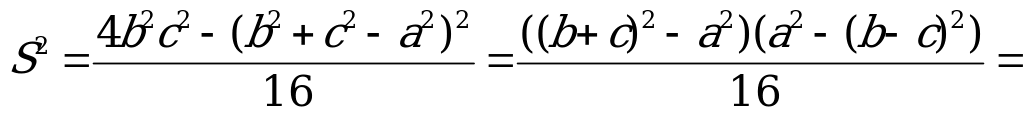Доклад на тему площадь треугольника

Видео:Геометрия 9 класс (Урок№14 - Теорема о площади треугольника.)Скачать

Определение площади треугольника

Площадь треугольника — это величина, которая
показывает какие размеры у треугольника.

Сейчас, на примере покажем, что такое площадь,
а также, как можно найти площадь треугольника.

Площадь треугольника, можно очень легко объяснить
на примере прямоугольного треугольника в клеточном поле.
Площадь, в нашем случае, будет равна количеству клеток.

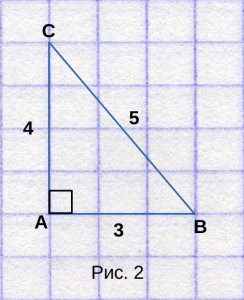
Для наглядности, нарисуем прямоугольный треугольник
ABC, со длинами сторон 3, 4 и 5, как на рисунке 2. Отметим, что он прямоугольный.

Посчитаем количество клеток, которые занимает треугольник.
3 полных клетки, и 4 неполных клетки, но для того, чтобы узнать
площадь треугольника в клеточном поле нам нужно узнать количество
полных клеток, которые занимает весь треугольник. Наша задача в том,
чтобы неполные клетки преобразовать в полные.

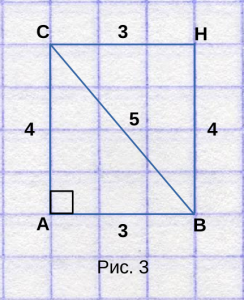
Для этого нарисуем второй треугольник, так,
чтобы получился прямоугольник, как на рисунке 3.

Как видим, весь прямоугольник занимает 12 полных клеток.

Формула площади прямоугольника равна произведению
одной стороны на другую — ​ ( S = ab ) ​,
поэтому площадь прямоугольника равна 3 * 4 = 12 клеткам.

Площадь треугольника, из которого состоит прямоугольник,
можно найти по другой формуле: ​ ( S = frac2 ab ) ​.
Подставив значения длин сторон, получаем — S = 0.5 * 3 * 4,
из чего следует, что S = 6 клетками, или же квадратным сантиметрам.

Прямоугольник можно условно разделить
на два треугольника, поэтому площадь треугольника
равна половине площади прямоугольника.

Формула площади треугольника — это формула,
по которой можно найти площадь треугольника.

Формулы площади треугольника применяют, только,
и только тогда, когда невозможно узнать площадь
треугольника, глядя на рисунок, или просто посчитав клетки.

Видео:Площадь треугольника. Как найти площадь треугольника?Скачать

Формулы площади треугольника

Ⅰ. Через высоту и основание

a — сторона, на которую падает высота,
b — высота.

Самая известная формула площади треугольника.
Зная только высоту и сторону, на которую падает
эта высота, можно найти площадь треугольника.

Ⅱ. Через все стороны и периметр

p — полупериметр, вычисляется по формуле: ​ ( p = frac ) ​,
a, b, c — стороны треугольника.

Это формулу, нужно использовать когда известны
все три стороны треугольника. Зная три стороны
треугольника можно найти периметр, а дальше
найти и площадь заданного треугольника.

Эту формулу площади также называют формулой Герона.

Ⅲ. Через две стороны и угол между ними

[ S = frac a cdot b cdot sin β ]

a, b — стороны между которыми расположен угол β,
sin β — синус угла β.

Формула применяется, когда известен
один из углов, и две стороны, образующие
этот угол. В некоторых задачах площадь
треугольника можно найти только по этой формуле.

Ⅳ. Через периметр и радиус вписанной окружности

[ S = r cdot frac

2 ]

r — радиус вписанной окружности,
P — периметр треугольника.

Тут даже не обязательно знать все стороны треугольника,
достаточно знать периметр и радиус описанной окружности.

Ⅴ. Через все стороны и радиус описанной окружности

abc — произведение всех сторон треугольника,
R — радиус описанной окружности.

Пожалуй, единственная формула, где площадь
треугольника можно найти только через радиус
описанной окружности и произведение трех сторон.

Ⅵ. Через сторону и два прилежащих к ней угла

a — сторона треугольника,
sin α — синус угла α,
sin β — синус угла β.

Готов поспорить, вы даже ни разу не видели этой формулы.
Эта очередная формула площади треугольника, применяется
в крайне редких случаях — когда известны два угла и сторона,
к которой эти углы примыкают.

Видео:9 класс, 12 урок, Теорема о площади треугольникаСкачать

Реферат по геометрии на тему «Площадь треугольника»

Просмотр содержимого документа
«Реферат по геометрии на тему «Площадь треугольника»»

Реферат по геометрии

1.Необходимость измерения площадей в древности и в современной

2. Справочная таблица: «Площадь треугольника».

3. Вывод формул площади треугольника, используемых в школьном

4. Понятие о вневписанной окружности.

5. Вывод некоторых формул площади треугольника через элементы

6. Примеры решения задач на применение формул площади треугольника.

7. Значение данной темы в развитии представлений о свойствах геометрических фигур.

Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.

Ещё 4-5 тыс. лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служил эталоном при измере- нии площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, ими можно заполнить плоскость без пробелов 1 .

Древние египтяне 4000 лет назад пользовались почти теми

же приемами, что и мы, для измерения площади прямоугольни-

ка, треугольника и трапеции: основание треугольника дели- а

л ось пополам и умножалось на высоту; для трапеции же сумма

параллельных сторон делилась пополам и умножалась на d

высоту. Для вычисления площади S четырехугольника со b

с торонами а, b, c, d (рис.1) применялась формула

S = , (1) (рис. 1)

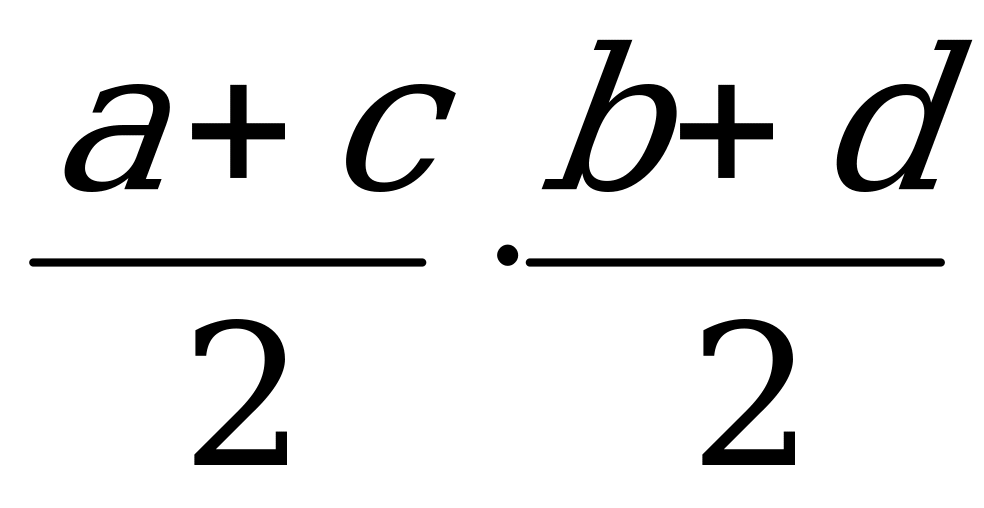
т. е. умножались полусуммы противоположных сторон. Эта формула верна только для прямоугольника. С её помощью можно вычислить приближённо площадь таких четырёхугольников, у которых углы близки к прямым.

Для определения площади S равнобедренного треугольника АВС, в котором

АВ = АС, египтяне пользовались приближённой формулой:

S = 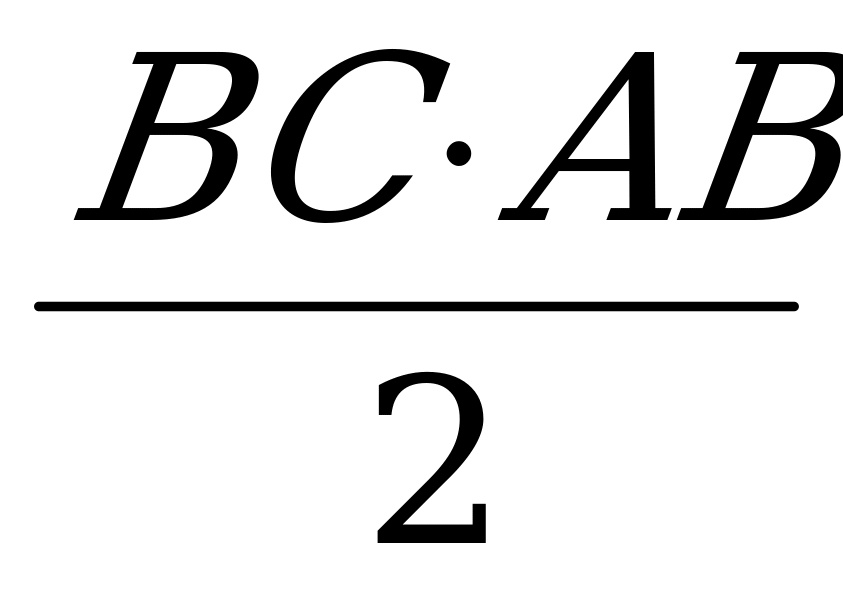. (2)

Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной АВ и высотой АD треугольника , иными словами, чем ближе вершина В ( и С ) к основанию В высоты из А. Вот почему приближённая формула (2) применима лишь для треугольников с сравнительно малым углом при вершине.

Потребность измерения расстояний и площадей приве-

л а к созданию и на Руси рукописей геометрического содержа-

ния чисто практического характера. Первые сведения о таких

рукописях относятся к XVI в. Спустя столетие, в 1629 г., а а 2 а 2

в сохранившейся рукописи «Книга сошного письма» имеется а

глава «О земном верстании, как земля верстать». В этой главе (рис. 2)

собраны правила измерения площадей фигур различной кон-

фигурации и приведён ряд примеров, как этими правилами S=a 2 + a 2 = a 2

пользоваться. Но выводов и обоснований указанных правил

нет. В рукописи рекомендуется производить измерение и вы-

числение площадей различных фигур посредством измерения площадей простейших

фигур: квадрата, прямоугольника, треугольника и трапеции. Площадь прямоуголь-ника согласно указаниям в этой рукописи следует вычислять путём выделения из

прямоугольника наибольшего квадрата, а площадь оставшегося после отсечения

квадрата прямоугольника вычислить, узнав, какую долю наибольшего квадрата составляет его площадь, посредством сравнения длины стороны квадрата и малого прямоугольника (см. рис.2, на котором обозначения даны современные).

Для вычисления площади треугольника в рукописи рекомендуется произведение большей и меньшей сторон разделить на два. Это правило даёт лишь приближённое значение истинного размера площади.

Из сказанного можно заключить, что точного измерения и вычисления площадей

треугольников и трапеций составители этой рукописи не знали.

Вопреки сохранившимся рукописям создание «русскими мастерами каменных

дел» различных грандиозных сооружений (кремлёвских стен и башен, храмов)

говорит о том что эти мастера обладали довольно основательными знаниями в области геометрии. Без таких знаний сооружение прекрасных зданий, как храм Василия Блаженного в Москве, вряд ли можно совершить.

В своей практической деятельности человек часто имеет дело с площадями.

Чтобы найти, например, урожайность с 1 га, надо знать площадь поля и сколько всего зерна собрано с этого поля. О площади, занимаемой каким — либо государством, мы узнаём из курса географии. Площадь поверхности стен в помещении нужно знать, например, для того, чтобы рассчитать необходимое для их покрытия количество краски, обоев или кафеля. Площадь поверхности дороги нужно знать, например, при расчёте необходимого для её покрытия количества асфальта. Что же такое площадь и как её находить? Чтобы упростить задачу, мы будем сначала рассматривать простые фигуры. Фигуру будем называть простой,

если её можно разбить на конечное число треугольников.

Для простых фигур площадь – это положительная величина, численное значение которой обладает следующими свойствами:

1) Равные фигуры имеют равные площади.

2) Если фигура разбивается на части, являющиеся простыми фигурами, то площадь этой фигуры равна сумме площадей её частей.

3) Площадь квадрата со стороной, равной единице измерения, равна единице.

Какие же единицы используются при изменении площадей?

Если сторона квадрата 1 см, то его площадь 1 см 2 ; если сторона квадрата 1 дм, то площадь 1 дм 2 . А 1 м 2 – это площадь квадрата со стороной 1 м, 1 км 2 – это площадь квадрата со стороной 1 км. Употребляются и такие единицы площади, как 1 гектар (1 га), 1 ар. 1 га – это площадь квадрата со стороной 100 м, а 1 ар – квадрата со стороной 10 м. 1 ар часто называют соткой. Она содержит 100 м 2 ; например, говорят: «Дачный участок имеет площадь 6 соток».

В справочной литературе мы находим старинные единицы площадей: 1 акр, 1 десятина.

Прямое измерение площадей на практике затруднено, поэтому применяются косвенные методы, наиболее употребительным из которых является вычисление площадей по формулам. Некоторые формулы вычисления площадей я приведу в своей работе.

Формулы площади треугольника.

1. S = ah_a

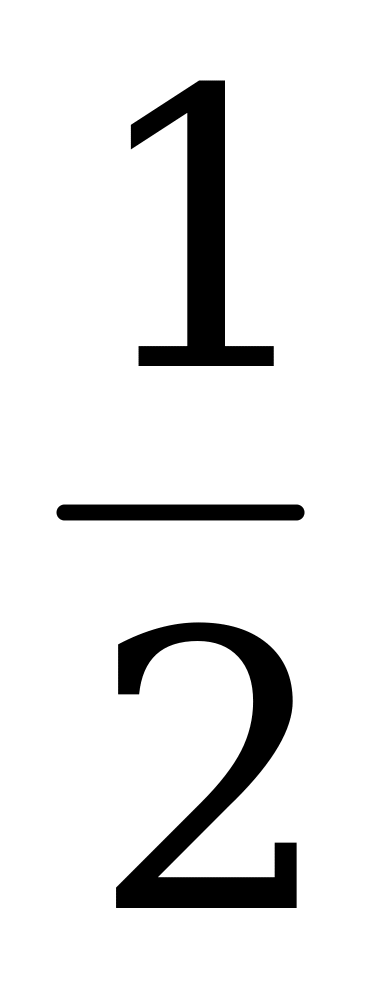
2. S = ab sin C

3. S = p r

4. S =

5. S = , p=

6. S =

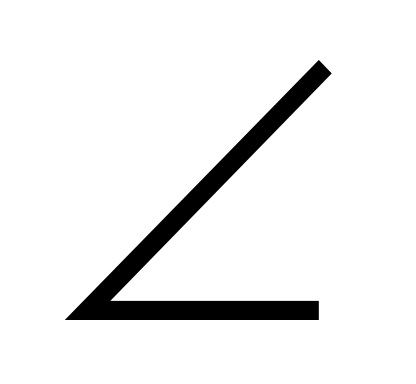
7. S =

8. S =

9. S = (h_a+h_b+h_c)

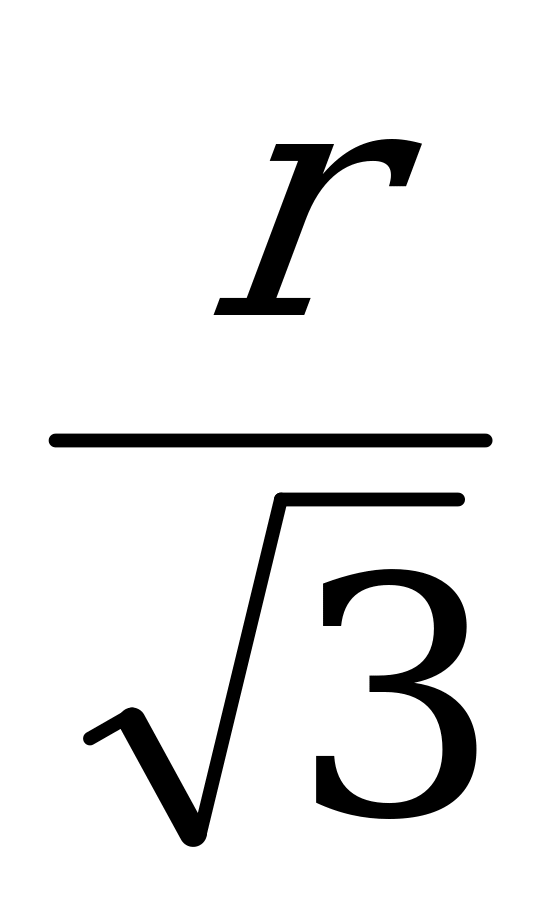
10. S = 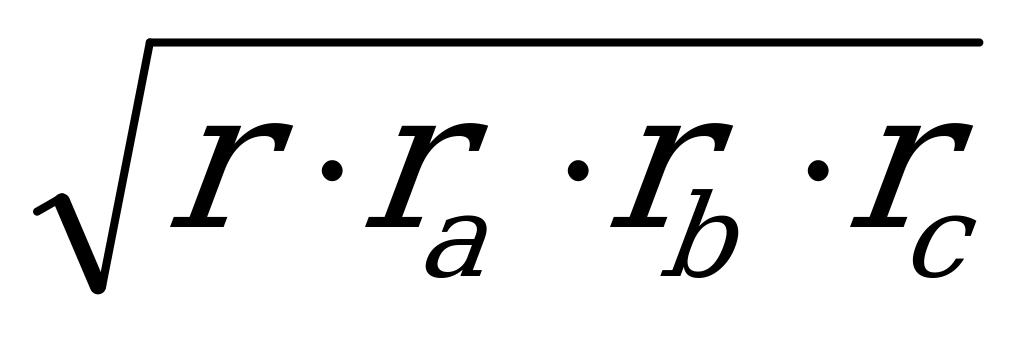, r_a , r_b , r_c – радиусы

11. S = r_a(p – a) = r_b(p – b) = r_c(p – c)

12. S =

13. S =

14. S =

15. S =

Условимся одну из сторон треугольника называть основанием, а перпендикуляр, проведённый из противоположной вершины к прямой, содержащей эту вершину,- высотой.

Выведем несколько формул площади треугольника, часто используемых при решении задач.

Площадь треугольника равна половине произведения

его основания на высоту. А К

Доказательство. Пусть АВС – данный треугольник,

а S — его площадь (рис. 3). Достроим треугольник h

АВС до параллелограмма. Площадь параллелограмма

А КВС равна сумме площадей треугольников АВС и С D a B

АВК. Так как эти треугольники равны, то площадь

параллелограмма равна удвоенной площади треуголь- (рис. 3)

ника АВС : S_АКВС = 2S = ah, так как высота паралле-

лограмма, соответствующая стороне ВС, равна высоте треугольника АВС, прове-дённой к стороне ВС. Поэтому

S = ah , (1)

где ВС = а, AD = h. Теорема доказана.

Cледствие 1. Площадь прямоугольного треугольника равна половине произведения его катетов.

Следствие 2. Треугольники, имеющие равные основания и равные высоты, равновелики.

Площадь треугольника равна половине произведения двух сторон на синус угла между ними .

Доказательство. Проведём в треугольнике АВС высоту

B D (рис.4,а). Имеем: S= АС . Из прямоугольного B

треугольника ABD : BD = AB 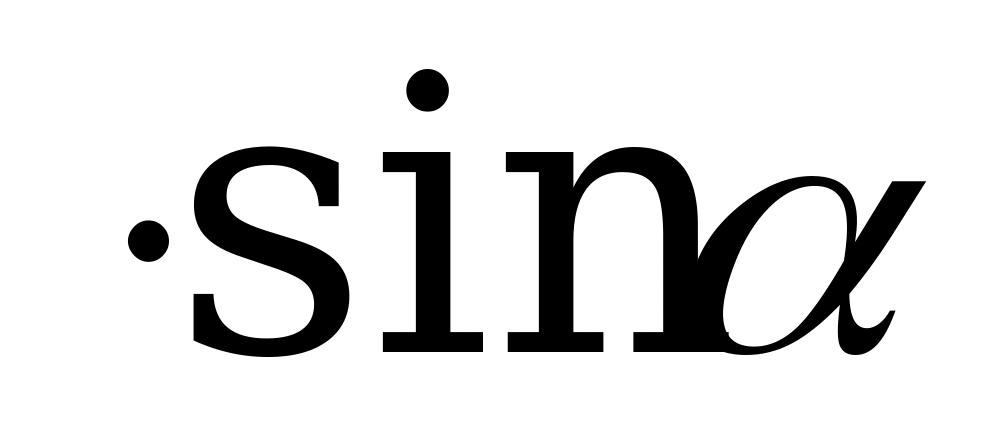, если угол

острый (рис.4, а), BD = AB ( — ), если угол

тупой (рис.4,б). Так как sin a

( ) = sin , то в C D А

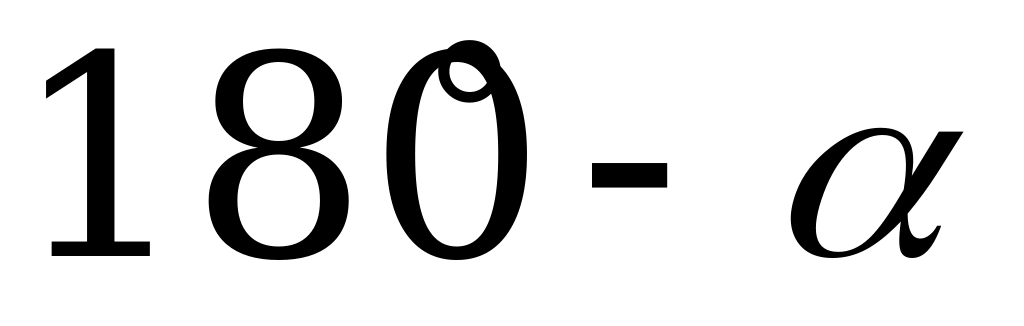
любом случае BD = AB 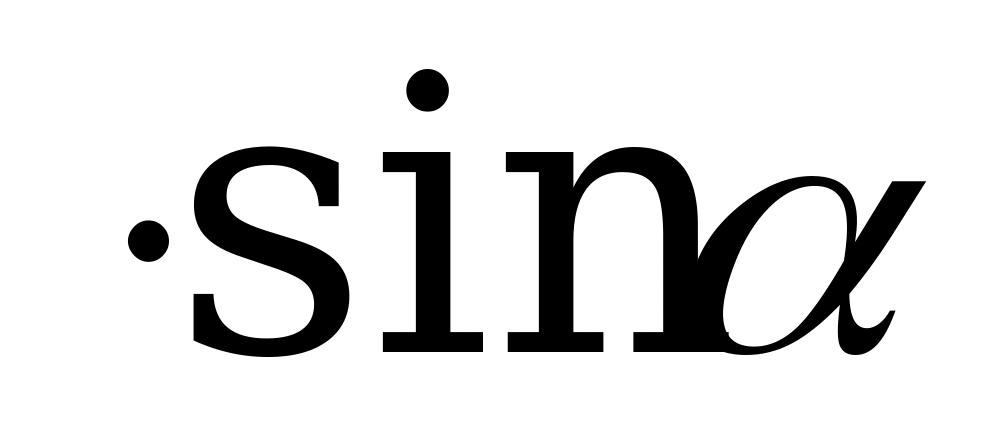.Следовательно, площадь (рис. 4, а)

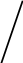
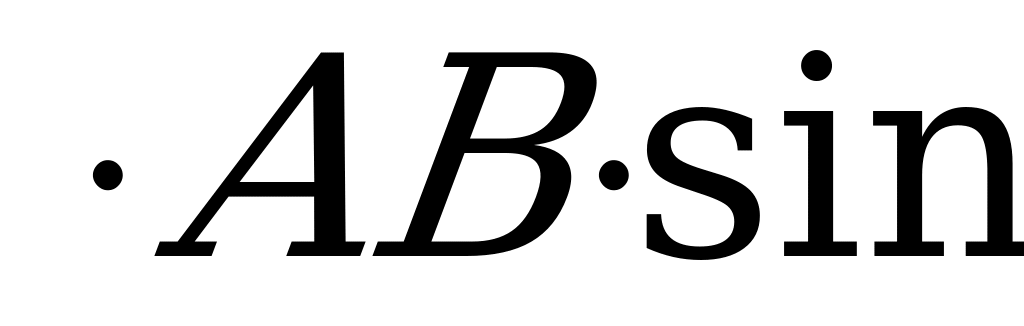
т реугольника S = AC A. В

S = bс C . (2)

а

Площадь треугольника равна произведению его полупериметра на радиус вписанной

о кружности:

S = pr , (3)

г де p = (a + b + c). В

Доказательство. Пусть О – центр

окружности, вписанной в треугольник, с а

r – её радиус (рис. 5). Соединив центр r

О с вершинами А, В и С, получим О r

треугольники АОВ, ВОС и АОС с

высотами, равными r. Согласно r r

свойству площадей A b С

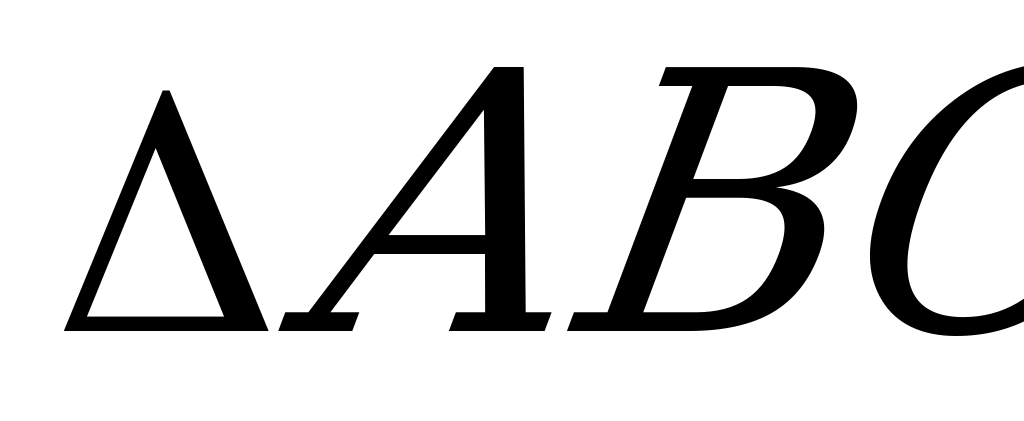
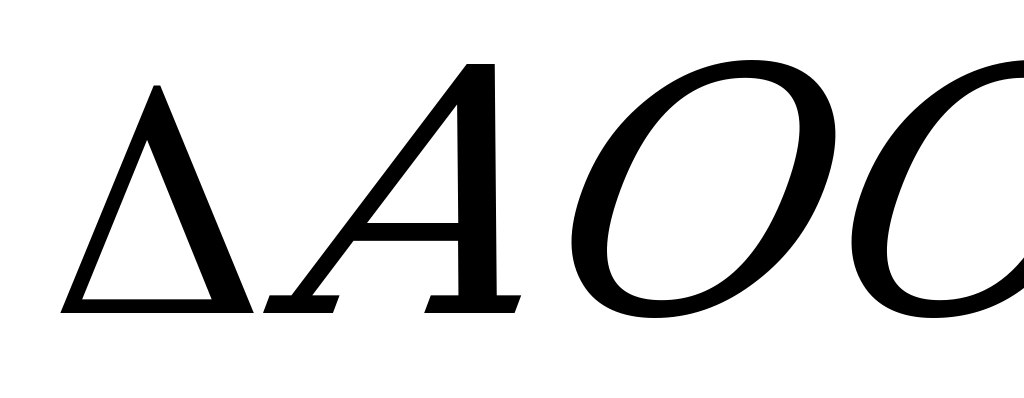
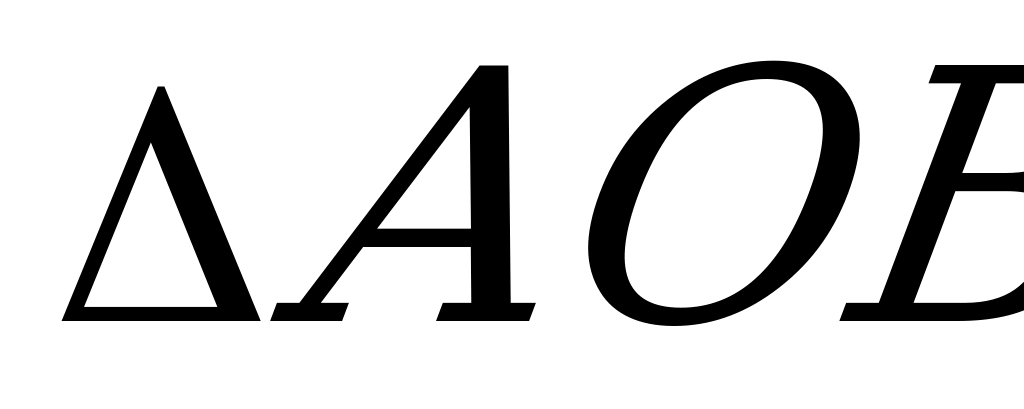
S = S + S +S = (a + b + c) = pr,

что и требовалось доказать.

Площадь треугольника равна произведению всех его сторон, деленному на учетверенный радиус описанной окружности

S = . (4)

Доказательство. согласно формуле (2)

S = bс C.

По теореме синусов

2R,

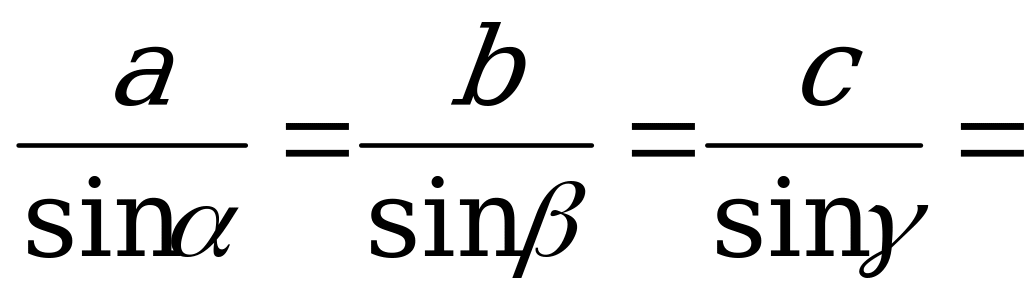
где R – радиус окружности, описанной около треугольника. Из равенства

sin = .

Подставляя выражение для в формулу (2), получим

S = .

Формула Герона. Площадь треугольника

S = 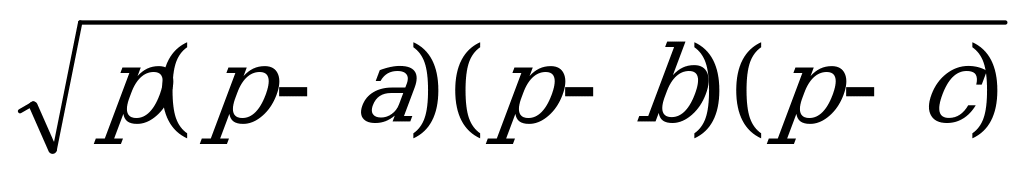, (5)

г де p = – половина периметра треугольника.

Доказательство. Из формулы S = bc C находим

sin = ;

по теореме косинусов a 2 = b 2 + c 2 – 2bc 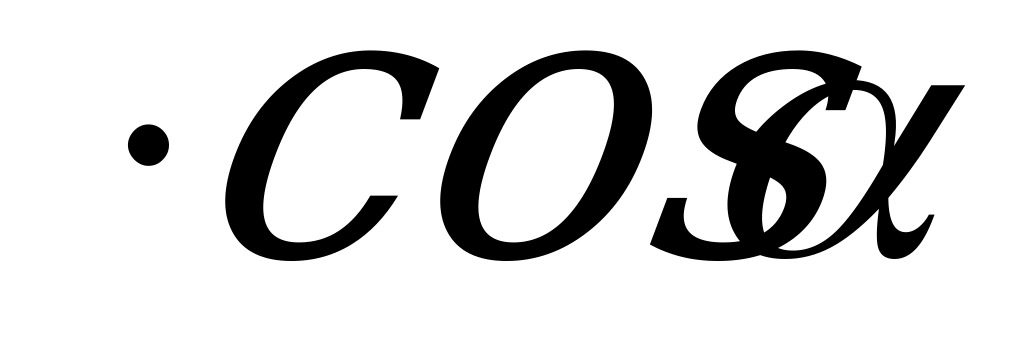, или

.

Используем основное тригонометрическое тождество 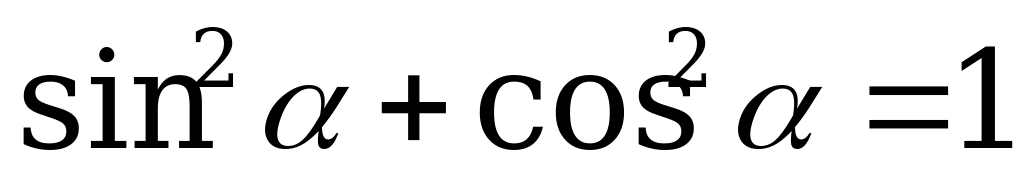. Получим

.

Отсюда, применяя формулу для разности квадратов, имеем

;

S = .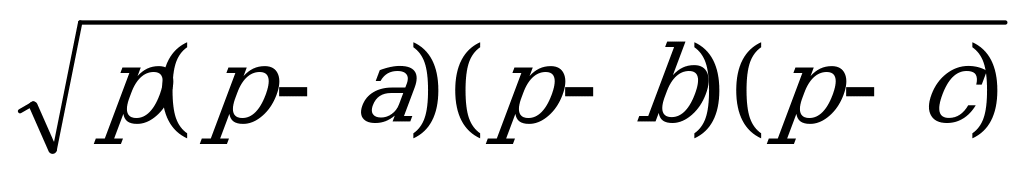

Формула Герона позволяет вычислить площадь треугольника по его трём

сторонам. Итак, для вычисления площади треугольника получены формулы (1) – (5).

Формулы (3) и (4) можно использовать для вычисления радиусов вписанной и

описанной окружностей, если известны стороны треугольника. Тогда его площадь

можно вычислить по формуле Герона, а затем найти , .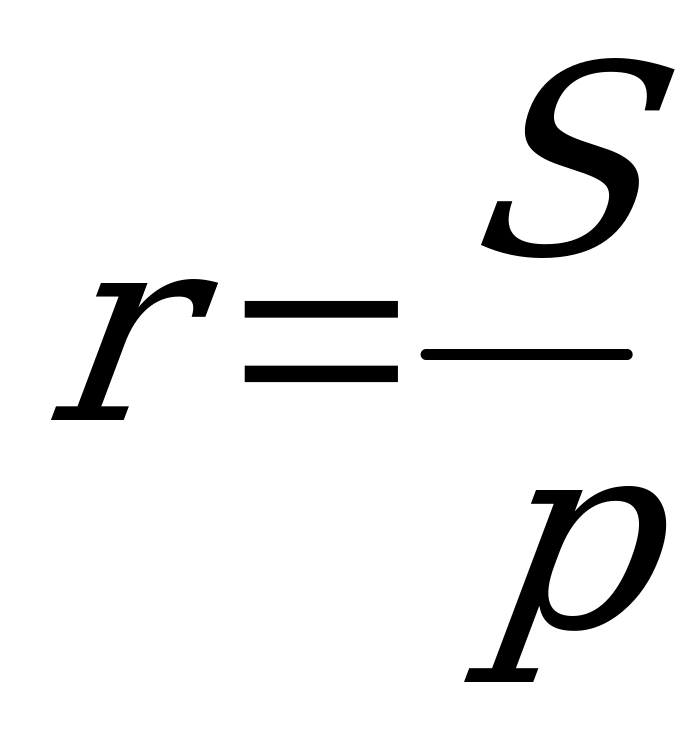

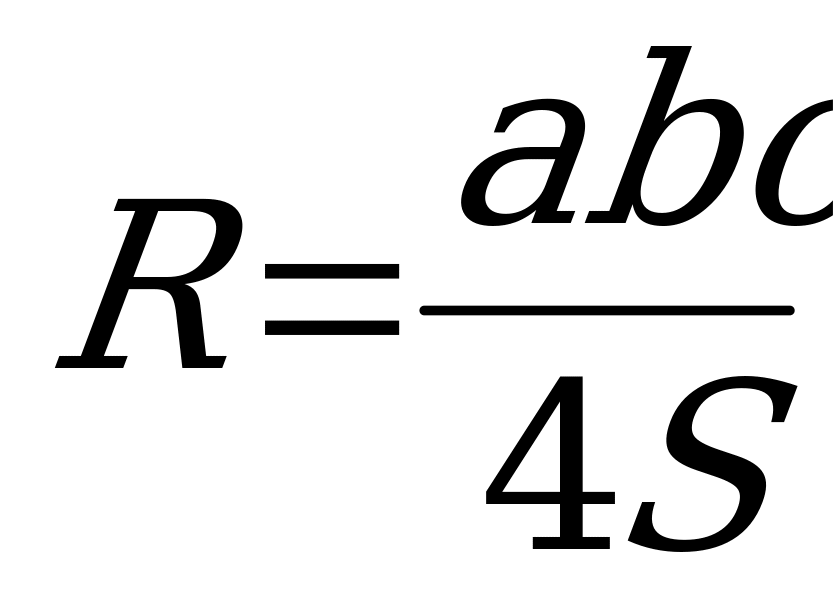
Решение некоторых типов геометрических задач, и, прежде всего задач на построение, связано с использованием этого понятия.

Опр. Вневписанной окружностью треугольника называется окружность, касающая-ся одной из его сторон и продолжений двух других.

Для каждого треугольника существует три вневписанных окружности, кото-рые расположены вне треугольника, почему они и получили название вневписанных.

Выясняется, что центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника. Рассматривая рисунок, замечаем, что центром окружности, вписанной в угол А, служит точка О_а (точка пересечения биссектрис внешних углов треугольника, не смежных с углом А); радиус этой окружности есть отрезок перпендикуляра, проведённого из точки О_а

к какой-либо стороне (или её продолжению):

O_c B O_a

Видео:Геометрия 8 класс (Урок№10 - Площадь треугольника.)Скачать

Как найти площадь треугольника. Формулы треугольника

Вы будете перенаправлены на Автор24

Видео:Площадь треугольника. Формула площади. Геометрия 8 класс.Скачать

Понятие площади

Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.

Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.

Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется

Тогда площадь треугольника равняется

Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.

Видео:Как найти площадь треугольника? #треугольник #математика #егэ #shorts #подготовкакегэ #огэ #площадьСкачать

Как найти площадь треугольника через высоту и основание

Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.

Математически это выглядит следующим образом

где $a$ — длина стороны, $h$ — высота, проведенная к ней.

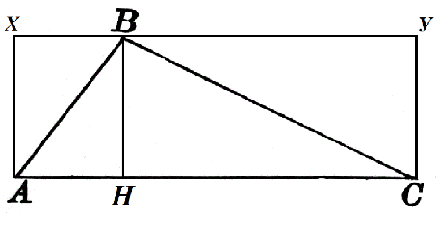
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.

Площадь прямоугольника $AXBH$ равняется $hcdot AH$, а прямоугольника $HBYC$ равняется $hcdot HC$. Тогда

$S_ABH=frachcdot AH$, $S_CBH=frachcdot HC$

Следовательно, искомая площадь треугольника, по свойству 2, равняется

$S=S_ABH+S_CBH=frachcdot AH+frachcdot HC=frachcdot (AH+HC)=fracαh$

Готовые работы на аналогичную тему

Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице

Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим

$S=fraccdot 9cdot 9=40,5$

Видео:100. Теорема о площади треугольникаСкачать

Формула Герона

Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом

здесь $ρ$ означает полупериметр этого треугольника.

Рассмотрим следующий рисунок:

По теореме Пифагора из треугольника $ABH$ получим

Из треугольника $CBH$, по теореме Пифагора, имеем

Из этих двух соотношений получаем равенство

Так как $ρ=frac$, то $α+β+γ=2ρ$, значит

По теореме 1, получим

Видео:8 класс, 14 урок, Площадь треугольникаСкачать

Площадь равностороннего треугольника

Площадь равностороннего треугольника определяется как произведение квадрата стороны с числом $frac<sqrt>$.

Математически это выглядит следующим образом

где $α$ – сторона треугольника.

Пусть нам дан равносторонний треугольник, у которого сторона равняется $α$. Проведем высоту $h$ (рис. 5).

Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора

Значит по теореме 1:

Найти площадь равностороннего треугольника, если его сторона равняется $2$.

Используя теорему 3, получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Дата последнего обновления статьи: 07 07 2021 Автор этой статьи

📽️ Видео

Геометрия 8 Площадь треугольникаСкачать

Площади фигур - треугольника, параллелограмма, трапеции, ромба. Формула Пика и ЕГЭСкачать

ПЛОЩАДЬ ТРЕУГОЛЬНИКА формула 9 класс геометрия АтанасянСкачать

Найдите площадь треугольника на рисунке ★ Два способа решенияСкачать

Геометрия 8. Урок 14 - Площадь треугольников. Формулы и задачи.Скачать

КАК найти площадь трапеции? Геометрия 8 класс | МатематикаСкачать

Как найти площадь треугольника без формулы?Скачать

11 класс, 47 урок, Формулы площади треугольникаСкачать

Геометрия 9 класс : Теорема о площади треугольникаСкачать

Площадь параллелограмма, треугольника, трапецииСкачать

Высшая математика. 3 урок. Аналитическая геометрия. Вычисление площади треугольникаСкачать

Площадь треугольника. Видеоурок по геометрии 8 классСкачать