Поток вектора через замкнутую поверхность куба

Рассмотрим теперь частный случай потока из маленького кубика и получим интересную формулу. Ребра куба пусть направлены вдоль осей координат (фиг. 3.5), координаты вершины, ближайшей к началу, суть х, у, z, ребро куба в направлении х равно Δx:, ребро куба (а точнее, бруска) в направлении у равно Δу, а в направлении z равно Δz. Мы хотим найти поток векторного поля С через поверхность куба. Для этого вычислим сумму потоков через все шесть граней. Начнем с грани 1 (см. фиг. 3.5). Поток наружу сквозь нее равен x-компоненте С с минусом, проинтегрированной по площади грани. Он равен

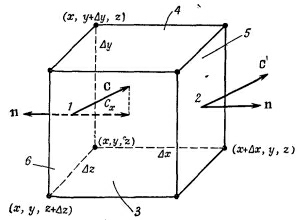
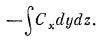Так как куб считается малым, этот интеграл можно заменить значением С_х в центре грани [эту точку мы обозначили (1)], умноженным на площадь грани ΔyΔz:

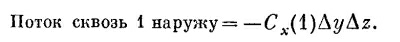Подобным же образом поток наружу через грань 2 равен

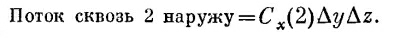Величины С_х(1) и С_х(2), вообще говоря, слегка отличаются. Если Δx достаточно мало, то можно написать

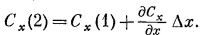Существуют, конечно, и другие члены, но в них входит (Δx) 2 и высшие степени Δx, и в пределе малых Δx ими запросто можно пренебречь. Значит, поток сквозь грань 2 равен

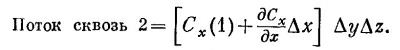Складывая потоки через грани 1 и 2, получаем

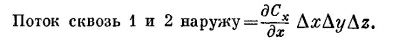Производную нужно вычислять в центре грани 1, т. е. в точке [х, y + (Δy/2), z+(Δz/2)]. Но если куб очень маленький, мы сделаем пренебрежимую ошибку, если вычислим ее в вершине (х, у, z).

Повторяя те же рассуждения с каждой парой граней, мы получаем

А общий поток через все грани равен сумме этих членов. Мы обнаруживаем, что

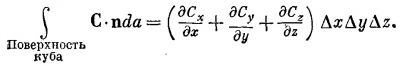Сумма производных в скобках как раз есть v·С, a ΔxΔyΔz=ΔV (объем куба). Таким образом, мы можем утверждать, что для бесконечно малого куба

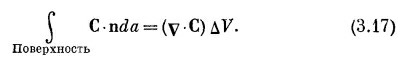Мы показали, что поток наружу с поверхности бесконечно малого куба равен произведению дивергенции вектора на объем куба. Теперь мы понимаем «смысл» понятия дивергенции вектора. Дивергенция вектора в точке Р — это поток С («истечение» С наружу) на единицу объема, взятого в окрестности Р.

Мы связали дивергенцию С с потоком С из бесконечно малого объема. Для любого конечного объема можно теперь использовать факт, доказанный выше, что суммарный поток из объема есть сумма потоков из отдельных его частей. Иначе говоря, мы можем проинтегрировать дивергенцию по всему объему. Это приводит нас к теореме, согласно которой интеграл от нормальной составляющей произвольного вектора по замкнутой поверхности может быть представлен также в виде интеграла от дивергенции вектора по объему, заключенному внутри поверхности. Теорему эту называют теоремой Гаусса.

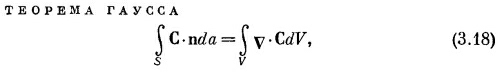где S — произвольная замкнутая поверхность, V — объем внутри нее.

Видео:Поток через замкнутую поверхность. Формула Остроградского-ГауссаСкачать

Поток вектора через замкнутую поверхность куба

Поток вектора напряженности электрического поля. Пусть небольшую площадку D S (рис.1.2) пересекают силовые линии электрического поля, направление которых составляет с нормалью n к этой площадке угол a . Полагая, что вектор напряженности Е не меняется в пределах площадки D S, определим поток вектора напряженности через площадку D S как

Поскольку густота силовых линий равна численному значению напряжённости E, то количество силовых линий, пересекающих площадку D S , будет численно равно значению потока D F _E через поверхность D S . Представим правую часть выражения (1.3) как скалярное произведение векторов E и D S = n D S , где n – единичный вектор нормали к поверхности D S . Для элементарной площадки d S выражение (1.3) принимает вид

Через всю площадку S поток вектора напряженности вычисляется как интеграл по поверхности

Поток вектора электрической индукции. Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля

В определениях потоков заметна некоторая неоднозначность, связанная с тем, что для каждой поверхности можно задать две нормали противоположного направления. Для замкнутой поверхности положительной считается внешняя нормаль.

Теорема Гаусса. Рассмотрим точечный положительный электрический заряд q , находящийся внутри произвольной замкнутой поверхности S (рис. 1.3). Поток вектора индукции через элемент поверхности d S равен
(1.4)

Составляющую d S_D = d S cos a элемента поверхности d S в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q .

Учитывая, что d S_D / r 2 равен элементарному телесному углу d w , под которым из точки нахождения заряда q виден элемент поверхности d S, преобразуем выражение (1.4) к виду d F _D = q d w / 4 p , откуда после интегрирования по всему окружающему заряд пространству, т. е. в пределах телесного угла от 0 до 4 p , получим

Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен заряду, заключенному внутри этой поверхности.

Если произвольная замкнутая поверхность S не охватывает точечный заряд q (рис. 1.4), то, построив коническую поверхность с вершиной в точке нахождения заряда, разделим поверхность S на две части: S₁ и S₂. Поток вектора D через поверхность S найдем как алгебраическую сумму потоков через поверхности S₁ и S₂:

.

Обе поверхности из точки нахождения заряда q видны под одним телесным углом w . Поэтому потоки равны

.

Поскольку при вычислении потока через замкнутую поверхность используется внешняя нормаль к поверхности, легко видеть, что поток Ф _{1D 2D} > 0. Суммарный поток Ф _D = 0. Это означает, что поток вектора электрической индукции через замкнутую поверхность произвольной формы не зависит от зарядов, расположенных вне этой поверхности.

Если электрическое поле создаётся системой точечных зарядов q ₁, q ₂, ¼ , q_n , которая охватывается замкнутой поверхностью S, то, в соответствии с принципом суперпозиции, поток вектора индукции через эту поверхность определяется как сумма потоков, создаваемых каждым из зарядов. Поток вектора электрической индукции через замкнутую поверхность произвольной формы равен алгебраической сумме зарядов, охваченных этой поверхностью:

(1.5)

Следует отметить, что заряды q_i не обязательно должны быть точечными, необходимое условие — заряженная область должна полностью охватываться поверхностью. Если в пространстве, ограниченном замкнутой поверхностью S, электрический заряд распределен непрерывно, то следует считать, что каждый элементарный объём d V имеет заряд . В этом случае в правой части выражения (1.5) алгебраическое суммирование зарядов заменяется интегрированием по объёму, заключённому внутри замкнутой поверхности S:

(1.6)

Выражение (1.6) является наиболее общей формулировкой теоремы Гаусса: поток вектора электрической индукции через замкнутую поверхность произвольной формы равен суммарному заряду в объеме, охваченном этой поверхностью, и не зависит от зарядов, расположенных вне рассматриваемой поверхности. Теорему Гаусса можно записать и для потока вектора напряженности электрического поля :

_.

Из теоремы Гаусса следует важное свойство электрического поля: силовые линии начинаются или заканчиваются только на электрических зарядах или уходят в бесконечность. Еще раз подчеркнем, что, несмотря на то, что напряжённость электрического поля E и электрическая индукция D зависят от расположения в пространстве всех зарядов, потоки этих векторов через произвольную замкнутую поверхность S определяются только теми зарядами, которые расположены внутри поверхности S.

Дифференциальная форма теоремы Гаусса. Отметим, что интегральная форма теоремы Гаусса характеризует соотношения между источниками электрического поля (зарядами) и характеристиками электрического поля (напряженностью или индукцией) в объеме V произвольной, но достаточной для формирования интегральных соотношений, величины. Производя деление объема V на малые объемы V_i , получим выражение

справедливое как в целом, так и для каждого слагаемого. Преобразуем полученное выражение следующим образом:

(1.7)

и рассмотрим предел, к которому стремится выражение в правой части равенства, заключенное в фигурных скобках, при неограниченном делении объема V. В математике этот предел называют дивергенцией вектора (в данном случае вектора электрической индукции D):

Дивергенция вектора D в декартовых координатах:

Таким образом выражение (1.7) преобразуется к виду:

_.

Учитывая, что при неограниченном делении сумма в левой части последнего выражения переходит в объемный интеграл, получим

Полученное соотношение должно выполняться для любого произвольно выбранного объема V . Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством

или для вектора напряженности электростатического поля

.

Эти равенства выражают теорему Гаусса в дифференциальной форме.

Отметим, что в процессе перехода к дифференциальной форме теоремы Гаусса получается соотношение, которое имеет общий характер:

_.

Выражение называется формулой Гаусса — Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем.

1) В чем заключается физический смысл теоремы Гаусса для электростатического поля в вакууме

2) В центре куба находится точечный заряд q . Чему равен поток вектора Е:

а) через полную поверхность куба; б) через одну из граней куба.

Изменятся ли ответы, если:

а) заряд находится не в центре куба, но внутри его ; б) заряд находится вне куба.

3) Что такое линейная, поверхностная, объемная плотности заряда.

4) Укажите связь объемной и поверхностной плотности зарядов.

5) Может ли поле вне разноименно и однородно заряженных параллельных бесконечных плоскостей быть отличным от нуля

6) Электрический диполь помещен внутрь замкнутой поверхности. Каков поток сквозь эту поверхность

Видео:Поток векторного поля через замкнутую поверхностьСкачать

Поток вектора через замкнутую поверхность куба

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

💥 Видео

Формула Остроградского-ГауссаСкачать

Семинар 12. Формула Остроградского — Гаусса.Скачать

Демидович №4441б: поток радиус-вектора через замкнутую поверхностьСкачать

Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Урок 223. Теорема ГауссаСкачать

Найти поток векторного поля через замкнутую поверхность S (нормаль внешняя).Скачать

Работа сил электрического поля. 10 класс.Скачать

Полярная система координатСкачать

#3.2 Найти поток вектора a=x^3i+y^3j=z^3k через всю поверхность куба в направлении внешней нормалиСкачать

Билет №02 "Теорема Гаусса"Скачать

Урок 222. Поток вектора напряженности электрического поляСкачать

Непосредственное вычисление потокаСкачать

Поток через замкнутую поверхность, формула ОстроградскогоСкачать

Урок 225. Задачи на поток вектора напряженности электрического поляСкачать

2421. Формула Остроградского.Скачать

Урок 34 (осн). Сила упругости. Закон ГукаСкачать

Физика. 10 класс. Поток вектора напряженности электрического поля. Теорема Гаусса /18.01.2021/Скачать

Демидович №4442: поток вектора через цилиндрСкачать