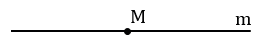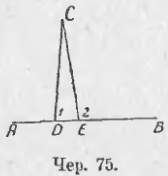Перпендикулярные прямые через треугольник

Примеры:

1. Даны прямая и точка на ней. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, M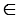m.

Построить: МPm.

Решение:

Произвольно строим с помощью линейки прямую m и отмечаем на ней точку М.

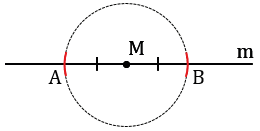
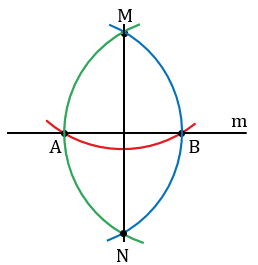
На лучах прямой m, исходящих из точки М, с помощью циркуля откладываем равные отрезки МА и МВ (МА = МВ). Для этого строим окружность с центром в точке М, при этом всю окружность строить не обязательно, достаточно сделать пометки по разные стороны от точки М (смотри выделенное красным).

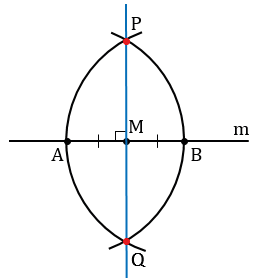
Затем строим две окружности с центрами в точках А и В радиуса АВ (полностью окружности строить необязательно, смотри выделенное фиолетовым и красным цветом).

Данные окружности пересекаются в двух точках, обозначим их Р и Q. Проведем с помощью линейки через точку М и одну из точек Р или Q прямую, например, МР.

Докажем, что прямая МР — искомая прямая, т.е. что МPm.

Рассмотрим треугольник АРВ.

АР = ВР, т.к. по построению это радиусы одинаковых окружностей, следовательно, АРВ — равнобедренный. По построению МА = МВ, т.е. МР — медиана равнобедренного треугольника, тогда по свойству равнобедренного треугольника МР и высота, т.е. МPm. Что и требовалось доказать.

2. Даны прямая и точка не лежащая на этой прямой. Построить прямую проходящую через данную точку и перпендикулярную к данной прямой.

Дано: прямая m, M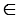m.

Построить: МNm.

Решение:

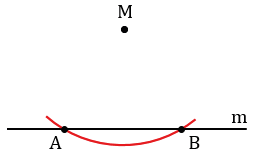
Произвольно строим с помощью линейки прямую m и отмечаем точку М, не лежащую на прямой m.

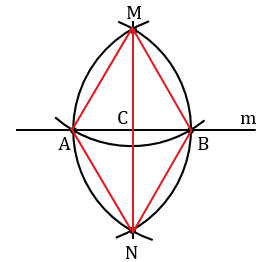
Далее строим окружность с центром в данной точке М, пересекающую прямую m в двух точках, которые обозначим буквами А и В (всю окружность строить необязательно, смотри выделенное красным цветом).

Затем построим две окружности с центрами в точках А и В, проходящие через точку М (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Эти окружности пересекутся в точке М и еще в одной точке, которую обозначим буквой N. Проведем прямую МN.

Докажем что, прямая МN — искомая, т.е. МNm.

В АМN и ВМN: АМ = АN = ВМ = ВN — радиусы, МN — общая, следовательно, АМN =ВМN (по трем сторонам), значит, углы ВМС и АМС равны (С точка пересечения прямых m и МN). Отсюда следует, что отрезок МС — биссектриса равнобедренного треугольника АМВ (АМ = ВМ — радиусы) с основанием АВ, тогда по свойству равнобедренного треугольника АМ — высота, значит, МNАВ, т.е. МNm.

Поделись с друзьями в социальных сетях:

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Математика

68. В п. 63 мы научились строить прямой угол. Так как две прямые, составляющие прямые углы, называются перпендикулярными друг другу (п. 60), то построение п. 63 можно выразить словами иначе: мы можем построить прямую, перпендикулярную к данной.

Мы теперь должны эту общую задачу разобрать подробнее и прежде всего разделим ее на две отдельных задачи:

1) Дана прямая и точка на ней, построить чрез данную точку перпендикуляр к данной прямой. (Можно ли и сколько?).

2) Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой. (Можно ил и сколько?).

В скобках указаны те вопросы, которые должны быть выяснены при выполнении построений.

69. 1-я задача . Дана прямая и точка на ней; построить чрез данную точку перпендикуляр к данной прямой.

Здесь остается повторить то построение, какое было дано в п. 63.

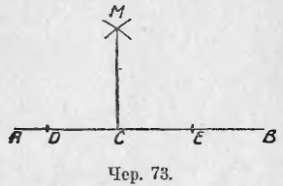
Пусть дана прямая AB и точка C на ней (чер. 73), построить чрез C перпендикуляр к AB.

От точки C откладываем по AB в разные стороны два произвольных, но равных отрезка CD = CE и затем, принимая последовательно точки D и E за центры, строим две окружности (или две дуги, достаточные для нахождения одной точки пересечения окружностей) одинаковыми радиусами, большими, чем отрезок CD. Точку пересечения M этих окружностей соединяем с C, тогда MC и есть искомый перпендикуляр, так как MC есть половина диагонали ромба, 3 вершины которого суть D, E и M.

Слово «перпендикуляр» пишут для сокращения знаком ⊥; мы построили

(CM перпендикуляр к AB).

Итак, выполнив это построение, мы можем признать, что чрез всякую точку, данную на прямой, можно построить к ней перпендикуляр (говорят иногда: восставить перпендикуляр к данной прямой). Остается еще вопрос: сколько?

Если луч CM повернуть около точки C в ту или другую сторону, то новые углы, составляемые этим лучом с прямою AB, уже не будут прямыми; поэтому заключаем, что возможно построить чрез точку прямой линии к этой прямой лишь один перпендикуляр .

70. 2-я задача . Дана прямая и точка вне ее; построить чрез данную точку перпендикуляр к данной прямой.

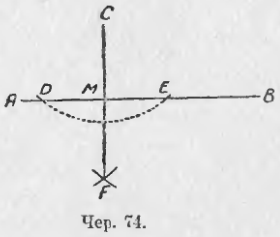
Пусть дана прямая AB и точка C вне ее (чер. 74); требуется чрез C построить перпендикуляр к AB.

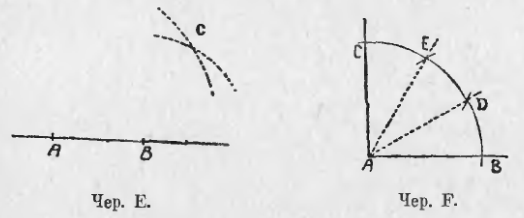
Задача сводится к построению такого ромба, чтобы его одна вершина расположилась в точке C и одна его диагональ шла по прямой AB. Для построения такого ромба опишем, принимая C за центр, окружность (или дугу), выбрав ее радиус столь большим, чтобы эта окружность пересекалась с прямою AB; пусть она пересечет прямую AB в точках D и E. Тогда будут найдены еще две вершины ромба. Затем, принимая последовательно за центры точки D и E, построим два круга (или две дуги) тем же самым радиусом и найдем точку их пересечения, расположенную по другую сторону от прямой AB сравнительно с точкою C, пусть эта точка есть F. Тогда все 4 вершины ромба найдены; остается построить его диагональ CF, она, как мы знаем, и будет перпендикулярна к AB, т. е. CF ⊥ AB или CM ⊥ AB.

Стороны ромба DC, CE, EF и FD нет надобности строить.

Выполнив указанное построение, мы должны признать, что из всякой точки, данной вне прямой, мы можем построить перпендикуляр к данной прямой (говорят иногда: опустить перпендикуляр на данную прямую). Остается еще вопрос: сколько?

Для решения этого вопроса допустим, что чрез точку C (чер. 75) построено: 1) CD ⊥ AB и 2) CE ⊥ AB. Тогда ∠CDB или ∠1 и ∠CEB или ∠2 оба должны быть прямыми и, следов., равны между собою. Но ∠CEB есть внешний угол для ∆CDE, а мы знаем (п. 49), что внешний угол треугольника должен быть больше внутреннего с ним несмежного. Это противоречие показывает, что наше допущение не верно, т. е. Нельзя построить чрез точку C двух перпендикуляров к прямой AB. Итак:

Чрез точку, данную вне прямой, можно построить только один перпендикуляр к этой прямой .

Замечание . Если, как мы получили в этом п., CF ⊥ AB (чер. 74), то, очевидно, и AB ⊥ CF.

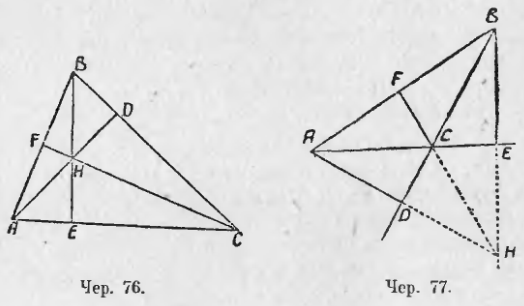
71. Построим какой-либо ∆ABC (чер. 76) и из каждой его вершины опустим перпендикуляр на противоположную сторону (здесь под именем сторона треугольника надо понимать бесконечную прямую). Каждый из этих перпендикуляров называется высотою треугольника. Следовательно, наша задача может быть выражена так: построить высоты треугольника. Если мы выполним построение перпендикуляров с возможною тщательностью, то в результате увидим, что по-видимому, все три высоты пересекаются в одной точке H, впоследствии мы выясним, что это свойство высот обязательно для всякого треугольника.

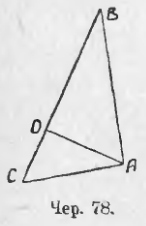
При построении высот может быть три случая: 1) все три высоты идут внутри треугольника (чер. 76); 2) две высоты BE и AD располагаются вне треугольника и общая точка H пересечения всех трех высот лежит вне треугольника (чер. 77) и 3) две высоты сливаются со сторонами треугольника (чер. 78), где BA ⊥ AC и CA ⊥ AB.

72. Для разбора вышеописанных трех случаев расположения высот условимся в обозначениях и названиях.
Прямой угол обозначают буквою d; тогда выпрямленный угол равен 2d, так как прямой угол есть половина выпрямленного угла. Если какой-либо угол больше прямого угла, то он называется тупым углом, а угол, меньший прямого угла, называется острым . Если ∠BAC (чер. 79) прямой, т. е., если ∠BAC = d, то ∠DAC > d и, следов., тупой, а ∠EAC сумма внутренних углов треугольника = 2d (или двум прямым углам ).

Ясно, что 3-й случай расположения высот в треугольнике, когда две его высоты сливаются со сторонами (чер. 78), имеет место, если ∠BAC треугольника прямой (∠BAC = d); такой треугольник с прямым углом называется прямоугольным . Так как сумма всех углов треугольника = 2d, а в этом случае ∠A прямой, или = d, то два другие угла (∠B и ∠C) в сумме составляют тоже прямой угол, а следовательно каждый из них в отдельности меньше прямого, или, другими словами, каждый из них острый угол.

Нетрудно теперь различать и два остальных случая: случай, данный на чер. 76, имеет место тогда, когда все 3 угла в треугольнике острые, а случай, данный на чер. 77, имеет место тогда, когда один из внутренних углов (на чер. 77 ∠BCA) тупой.

Ясно также, что если в треугольнике один угол тупой (или > d), то сумма двух других углов должна быть 1-й признак. Если два катета одного прямоугольного треугольника соответственно равны двум катетам другого, то эти прямоугольные треугольники равны.

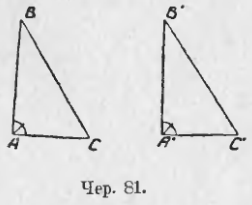
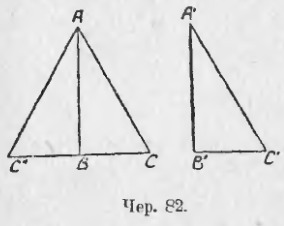
В самом деле это тот же самый признак, знакомый нам: если 2 стороны и угол между ними одного треугольника равны соответственно двум сторонам и углу между ними другого, то треугольники равны. Теперь про углы не говорится потому, что между катетами расположены прямые углы, а они всегда равны (на чер. 81). ∠A = ∠A’, как прямые, и достаточно для равенства ∆ABC и ∆A’B’C’ знать, что AB = A’B’ и AC = A’C’).

2-й признак. Если катет и прилежащий острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого, то эти прямоугольные треугольники равны.

Это опять-таки знакомый нам признак: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого треугольника, то эти треугольники равны. Теперь про равенство углов, прилегающих к равным катетам у другого конца каждого, не говорится, так как эти углы прямые, а они всегда равны (на чер. 81, где ∠A и ∠A’ прямые, достаточно для равенства треугольников знать, что AB = A’B’ и ∠B = ∠B’).

Можно вместо прилежащих углов к катетам взять углы, противолежащие этим катетам: если ∠C = ∠C’, то и ∠B = ∠B’, так как ∠B + ∠C = d и ∠B’ + ∠C’ = d.

Признак равенства треугольников по трем равным сторонам здесь нет нужды применять: мы уже знаем, что для равенства прямоугольных треугольников достаточно знать равенство двух сторон, а именно двух катетов (1-й признак).

3-й признак. Если гипотенуза и острый угол одного треугольника соответственно равны гипотенузе и острому углу другого, то эти прямоугольные треугольники равны.

Этот признак является следствием общего признака: если 2 угла и сторона между ними одного треугольника соответственно равны двум углам и стороне между ними другого, то эти треугольники равны. В самом деле, пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 81), у которых BC = B’C’ и ∠С = ∠С’. Так как мы знаем, что ∠B + ∠C = d (сумма всех трех внутренних углов ∆ABC = 2d, но ∠A = d, следов., ∠B + ∠C = d) и ∠B’ + ∠C’ = d (ибо ∠A’ = d), а нам известно, что ∠C = ∠C’, то отсюда приходим к заключению, что ∠B = ∠B’ и тогда сторона BC и два прилегающих к ней угла ∠C и ∠B одного треугольника равны соответственно стороне B’C’ и двум прилегающим к ней углам другого ∠C’ и ∠B’, а мы знаем, что в этом случае ∆ABC = ∆A’B’C’.

4-й признак. Если гипотенуза и катет одного прямоугольного треугольника равны соответственно гипотенузе и катету другого, то такие прямоугольные треугольники равны.

Этот признак удобнее всего выяснить следующим образом. Пусть имеем 2 прямоугольных треугольника ABC и A’B’C’ (чер. 82), причем ∠B = d и ∠B’ = d, у которых AC = A’C’ и AB = A’B’. Приложим ∆A’B’C’ и ∆ABC так, чтобы у них совпали равные катеты, т. е. A’B’ совпал бы с AB, и сами треугольники расположились бы по разные стороны от прямой AB, для этого иногда (напр., в случае, данном на чертеже) придется ∆A’B’C’ перевернуть другою стороною. Тогда сторона B’C’ должна пойти по такому направлению BC», чтобы ∠ABC» оказался прямым (ибо ∠B’ = d), а, следов., ∠CBC» оказался бы выпрямленным, т. е. Направление BC» должно быть продолжением стороны CB. Если точка C’ попадет в точку C», то, построив сторону AC», получим ∆ABC», равный ∆A’B’C’. Так как CBC» есть прямая линия, то получим еще ∆ACC», у которого сторона AC = AC», потому что AC» есть гипотенуза A’C’ треугольника A’B’C’, помещенного в положение ABC». Следовательно, ∆ACC» равнобедренный, а в таком случае углы при его основании равны, т. е. ∠C = ∠C», или ∠C = ∠C’. Оказалось, что у ∆ABC и ∠A’B’C’ имеется еще по равному острому углу, а в таком случае, на основании предыдущего признака, мы можем заключить, что ∆ABC = ∆A’B’C’.

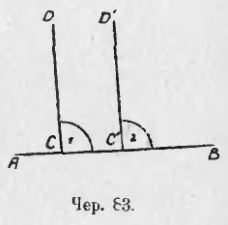
75. Пусть построено: 1) CD ⊥ AB и 2) C’D’ ⊥ AB (чер. 83); тогда, напр., ∠1 = ∠2, так как оба они прямые. Но эти углы суть соответственные при прямых CD и C’D’, пересеченных секущею AB, – следов., CD || C’D’.

Наоборот, пусть построено: 1) CD || C’D’ и 2) AB ⊥ CD (чер. 83); тогда AB должна пересечь и прямую C’D’ (п. 32, 1), напр. в точке C’. Легко увидим, что ∠2 = ∠1, так как эти углы соответственные при параллельных CD и C’D’ и секущей AB, но ∠1 = d, так как AB ⊥ CD, – следов., и ∠2 = d, т. е. AB ⊥ C’D’.
Поэтому имеем два заключения:

1) Два перпендикуляра к прямой параллельны.

2) Прямая, перпендикулярная к одной из параллельных, перпендикулярна и к другой.

76. Упражнения.

1. Построить прямоугольный ∆ по катетам.
2. Построить прямоугольный ∆ по катету и одному из острых углов.
3. Построить прямоугольный ∆ по гипотенузе и острому углу.
4. Построить прямоугольный ∆ по гипотенузе и катету.
5. Построить высоты параллелограмма. Указать среди них равные.
6. Задачу «построить перпендикуляр к данной прямой чрез данную вне ее точку» можно решить следующим построением: на данной прямой берем 2 произвольных точки A и B (чер. E) и, принимая их последовательно за центры, построим два круга радиусами AC и BC, где C данная точка. Окончить это построение и выяснить его справедливость.
7. Разделить прямой угол на 3 равных части.

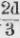
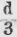
Третью часть прямого угла легко построить: каждый внутренний угол равностороннего треугольника = , а его половина = . Наиболее удобное расположение построения следующее: принимая вершину A прямого угла за центр (чер. F), строим произвольным радиусом окружность: затем, принимая за центры точки C и B – точки пересечения построенной окружности со сторонами прямого угла – строим тем же радиусом дуги, пересекающие построенную окружность в точках D и E. Тогда ∆AEB и ∆ACD равносторонние, и лучи AD и AE делят прямой ∠A на 3 равных части.

Видео:Перпендикулярные прямыеСкачать

Перпендикулярные прямые через треугольник

Из всех возможных положений прямой, пересекающей плоскость, отметим случай, когда прямая перпендикулярна к плоскости, и рассмотрим свойства проекций такой прямой.

На рис. 185 задана плоскость, определяемая двумя пересекающимися прямыми AN и AM, причем AN является горизонталью, а AM — фронталью этой плоскости. Прямая АВ, изображенная на том же чертеже, перпендикулярна к AN и к AM и, следовательно, перпендикулярна к определяемой ими плоскости.

Перпендикуляр к плоскости перпендикулярен к любой прямой, проведенной в этой плоскости. Но чтобы при этом проекция перпендикуляра к плоскости общего положения оказалась перпендикулярной к одноименной проекции какой-либо прямой этой плоскости, прямая должна быть горизонталью, или фронталью, или профильной прямой плоскости. Поэтому, желая построить перпендикуляр к плоскости, берут в общем случае две такие прямые (например, горизонталь и фронталь, как это показано на рис. 185).

Итак, у перпендикуляра к плоскости его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, фронтальная проекция перпендикулярна к фронтальной проекции фронтали, профильная проекция перпендикулярна к профильной проекции профильной прямой этой плоскости.

Очевидно, в случае, когда плоскость выражена следами (рис. 186), мы получаем следующий вывод: если прямая перпендикулярна к плоскости, то горизонтальная проекция этой прямой перпендикулярна к горизонтальному следу плоскости, а фронтальная проекция перпендикулярна к фронтальному следу плоскости.

Итак, если в системе π₁ п₂ горизонтальная проекция прямой перпендикулярна к горизонтальному следу и фронтальная проекция прямой перпендикулярна к фронтальному следу плоскости, то в случае плоскостей общего положения (рис. 186), а также горизонтально и фронтально-проецирующих прямая перпендикулярна к плоскости. Но для профильно-проецирующей плоскости может оказаться, что прямая к этой плоскости не перпендикулярна, хотя проекции прямой соответственно перпендикулярны к горизонтальному и фронтальному следам плоскости. Поэтому в случае профильно-проецирующей плоскости надо рассмотреть также взаимное положение профильной проекции прямой и профильного следа данной плоскости и лишь после этого установить, будут ли перпендикулярны между собой данные прямая и плоскость.

Очевидно (рис. 187), горизонтальная проекция перпендикуляра к плоскости сливается с горизонтальной проекцией линии ската, проведенной в плоскости через основание перпендикуляра.

На рис. 186 из точки А проведен перпендикуляр к пл. a (А»С» ⊥ f»_0a , А’С’ ⊥ h’_0a ) и показано построение точки Е, в которой перпендикуляр АС пересекает пл. а. Построение выполнено с помощью горизонтально-проецирующей пл. β, проведенной через перпендикуляр АЕ.

На рис. 188 показано построение перпендикуляра к плоскости, определяемой треугольником АВС. Перпендикуляр проведен через точку А.

Так как фронтальная проекция перпендикуляра к плоскости должна быть перпендикулярна к фронтальной проекции фронтали плоскости, а его горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали, то в плоскости через точку А проведены фронталь с проекциями A’D’ и A»D» и горизонталь А»Е», А’Е’. Конечно, эти прямые не обязательно проводить именно через точку А.

Далее проведены проекции перпендикуляра: M»N» ⊥ A»D», M’N’ ⊥ А’Е’. Почему проекции на рис. 188 на участках A»N» и А’М’ показаны штриховыми линиями? Потому, что здесь рассматривается плоскость, заданная треугольником АВС, а не только этот треугольник: перпендикуляр находится частично перед плоскостью, частично за ней.

На рис. 189 и 190 показано построение плоскости, проходящей через точку А перпендикулярно к прямой ВС. На рис. 189 плоскость выражена следами. Построение начато с проведения через точку А горизонтали искомой плоскости: так как горизонтальный след плоскости должен быть перпендикулярен к В’С’ то и горизонтальная проекция горизонтали должна быть перпендикулярна к В’С’. Поэтому A’N’ ⊥ В’С. Проекция A»N» || оси х, как это должно быть у горизонтали. Затем проведен через точку N» (N» — фронтальная проекция фронтальною следа горизонтали AN) след f’_0a ⊥ »ѻ, получена точка Х_a и проведен след h’_0a || A’N’ (h’_0a ⊥ В’С’).

На рис. 190 плоскость определена ее фронталью AM и горизонталью AN. Эти прямые перпендикулярны к ВС (А»М» ⊥ »ѻ, A’N’ ⊥ В’С); определяемая ими плоскость перпендикулярна к ВС.

Так как перпендикуляр к плоскости перпендикулярен к каждой прямой, проведенной в этой плоскости, то, научившись проводить плоскость перпендикулярно к прямой, можно воспользоваться этим для проведения перпендикуляра из некоторой точки А к прямой общего положения ВС. Очевидно, можно наметить следующий план построения проекций искомой прямой:

1) через точку А провести плоскость (назовем ее ϒ), перпендикулярную к ВС;

2) определить точку К пересечения прямой ВС с пл. ϒ;

3) соединить точки А и К отрезком прямой линии.

Прямые АК и ВС взаимно перпендикулярны.

Пример построения дан на рис. 191. Через точку А проведена плоскость (ϒ), перпендикулярная к ВС. Это сделано при помощи фронтали, фронтальная проекция A»F» которой проведена перпендикулярно к фронтальной проекции »ѻ и горизонтали, горизонтальная проекция которой перпендикулярна к В’С’.

Затем найдена точка К, в которой прямая ВС пересекает пл. ϒ. Для этого через прямую ВС проведена горизонтально-проецируюшая плоскость β (на чертеже она задана только горизонтальным следом β’). Пл. β пересекает пл. ϒ по прямой с проекциями 1’2‘ и 1″2″. В пересечении этой прямой с прямой ВС получается точка К. Прямая АК является искомым перпендикуляром к ВС. Действительно, прямая АК пересекает прямую ВС и находится в пл. ϒ, перпендикулярной к прямой ВС; следовательно, АК ⊥ ВС.

На рис. 192 изображены плоскость общего положения а, проходящая через точку А, и перпендикуляр AM к этой плоркости, продолженный до пересечения с пл. п₁, в точке В’.

Угол ф₁ между пл. а и пл. п₁ и угол ф между прямой AM и пл. п₁ являются острыми углами прямоугольного треугольника В’АМ’ и, следовательно, ф₁ +ф = 90°. Аналогично, если пл. а составляет с пл. п₂ угол σ₂, а прямая AM, перпендикулярная к а, составляет с пл. п₂ угол σ, то σ₂ + σ = 90°. Из этого, прежде всего, следует, что плоскость общею положения, которая должна составлять с пл. п₁ угол ф₁ а с пл. п₂ угол σ₂, может быть построена, лишь если 180° > Ф₁ + σ2 > 90°.

Действительно, складывая почленно Ф₁ + Ф = 90° и σ₂ + σ = 90°, получим Ф₁ + σ₂ + Ф + σ = 180°, т. е. Ф₁ + σ₂ 90°. Если взять Ф₁ + σ₂ =90°, то получится профильно-проецирующая плоскость, а если взять Ф₁ + σ₂ = 180°, то получится профильная плоскость, т. е. в обоих этих случаях плоскость не общего положения, а частного.

ПОСТРОЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ ПЛОСКОСТЕЙ

Построение плоскости β, перпендикулярной к плоскости a, может быть произведено двумя путями: 1) пл. β проводится через прямую, перпендикулярную к пл. а; 2) пл. β проводится перпендикулярно к прямой, лежащей в пл. а или параллельной этой плоскости. Для получения единственного решения требуются дополнительные условия.

На рис. 193 показано построение плоскости, перпендикулярной к плоскости, заданной треугольником CDE. Дополнительным условием здесь служит то, что искомая плоскость должна проходить через прямую А В. Следовательно, искомая плоскость определяется прямой АВ и перпендикуляром к плоскости треугольника. Для проведения этого перпендикуляра к пл. CDE в ней взяты фронталь CN и горизонталь СМ: если B»F» ⊥ C“N» и B’F’⊥C’M’, то BF⊥ пл. CDE.

Образованная пересекающимися прямыми АВ и BF плоскость перпендикулярна к пл. СОЕ, так как проходит через перпендикуляр к этой плоскости. На рис. 194 горизонтально-проецирующая плоскость β проходит через точку К перпендикулярно к плоскости, заданной треугольником АВС. Здесь дополнительным условием являлась перпендикулярность искомой плоскости сразу к двум плоскостям: к пл. АВС и к пл. п₁. Поэтому и ответом служит горизонтально-проецирующая плоскость. А так как она проведена перпендикулярно к горизонтали AD, т. е. к прямой, принадлежащей пл. АВС, то пл. β перпендикулярна к пл. АВС.

Может ли перпендикулярность одноименных следов плоскостей служить признаком перпендикулярности самих плоскостей?

К очевидным случаям, когда это так, относится взаимная перпендикулярность двух горизонтально-проецирующих плоскостей, у которых горизонтальные следы взаимно перпендикулярны. Также это имеет место при взаимной перпендикулярности фронтальных следов фронтально-проецирующих плоскостей; эти плоскости взаимно перпендикулярны.

Рассмотрим (рис. 195) горизонтально-проецирующую плоскость β, перпендикулярную к плоскости общего положения а.

Если пл. β перпендикулярна к пл. л, п₁ пл. а, то β⊥h’_0a как к линии пересечения пл. а и пл. п₁. Отсюда h’_0a ⊥ β и, следовательно, h’_0a ⊥ β , как к одной из прямых в пл. β.

Итак, перпендикулярность горизонтальных следов плоскости общего положения и горизонтально-проецирующей соответствует взаимной перпендикулярности этих плоскостей.

Очевидно, перпендикулярность фронтальных следов фронтально-проецирующей плоскости и плоскости общего положения также соответствует взаимной перпендикулярности этих плоскостей.

Но если одноименные следы двух плоскостей общего положения взаимно перпендикулярны, то самые плоскости не перпендикулярны между собой, так как здесь не соблюдается ни одно из условий, изложенных в начале этого параграфа.

В заключение рассмотрим рис. 196. Здесь имеет место случай взаимной перпендикулярности одноименных следов в обеих их парах и перпендикулярности самих плоскостей: обе плоскости особого (частного) положения — профильная ϒ и профильно-проецирующая а.

📺 Видео

Перпендикулярные прямые. 6 класс.Скачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

7 класс, 12 урок, Перпендикулярные прямыеСкачать

Наклонная, проекция, перпендикуляр. 7 класс.Скачать

6 класс. Математика. Перпендикулярные прямые. Построение. Тупоугольный треугольник.Скачать

Эксперт (Короткометражка, Русский дубляж)Скачать

6 класс, 43 урок, Перпендикулярные прямыеСкачать

№194. Начертите треугольник. Через каждую вершину этого треугольника с помощью чертежногоСкачать

Перпендикулярные прямые. Перпендикуляр. Теорема о перпендикулярной прямой проходящей через точку.Скачать

6 класс. Математика. Перпендикулярные прямые. Построение. Остроугольный треугольник.Скачать

КАК ПОСТРОИТЬ ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕ? Примеры | МАТЕМАТИКА 6 классСкачать

6 .7 кл Построение параллельных прямых.Как построить параллельные прямыеСкачать

Взаимно перпендикулярные плоскости. Определение кратчайшей расстоянии от точки до прямойСкачать

Геометрия 7 класс (Урок№7 - Перпендикулярные прямые.)Скачать

6 класс. Математика. Перпендикулярные прямые. Построение. Прямоугольный треугольник.Скачать

Теорема о трех перпендикулярах. Признак перпендикулярности плоскостей | Математика | TutorOnlineСкачать

Перпендикулярные прямые - 7 класс геометрияСкачать

Тема ПЕРПЕНДИКУЛЯРНЫЕ ПРЯМЫЕСкачать