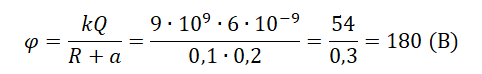Потенциал электрического поля в центре окружности

По тонкому проволочному кольцу равномерно распределен заряд с линейной плотностью τ = 100 пКл/м. Определить потенциал Φ электрического поля в центре кольца.

Эта задача была размещена посетителями в разделе Решаем вместе 8 октября 2007 года.

Потенциал в центре проволочного кольца определим по принципу суперпозиции, разбив кольцо на элементарные участки с зарядом q_i. Получим формулу (на рисунке слева), в которой:

i — количество разбиений,

потенциал Φ_i, создаваемый в центре кольца элементарным зарядом q_i, равен:

Из формулы линейной плотности заряда кольца

выразим:

Произведем суммирование Φ:

Выполнив расчеты, получим: Φ = 5.65 В.

Видео:Потенциал электрического поля. 10 класс.Скачать

Потенциал электрического поля в центре окружности

2016-12-11
Найти напряженность и потенциал электрического поля на оси равномерно заряженного тонкого кольца радиуса $R$, на расстоянии $x$ от его центра. Заряд кольца $Q$.

Разобьем кольцо на малые, равные (для удобства подсчета) фрагменты, такие, что заряды на этих участках можно считать точечными, и воспользуемся принципом суперпозиции:

где $vec_$ — напряженность в точке А, отстоящей на расстояние х от центра О, $vec_$ — напряженность электрического поля, создаваемая в точке А зарядом i-го фрагмента.

Вектор $vec$ направлен вдоль оси кольца. Это утверждение следует либо из соображений симметрии, либо из рассмотрения правой части (1). Действительно, на каждый i-ый участок кольца найдется симметричный ему участок. Таким образом, $sum vec_$ разбивается на пары векторов, сумма которых направлена вдоль оси. Следовательно, $sum vec_$ так же направлена вдоль оси.

Спроецируем (1) на ось:

$E = sum E_ = sum E_ cos alpha = cos alpha sum E_ = cos alpha sum frac <R^+ x^> = frac < sqrt<R^+ x^>> cdot frac<R^+x^> sum Delta Q_ = frac<(R^+x^)^>$. (2)

Видео:Билет №03 "Потенциал"Скачать

Электростатическое поле точечного заряда и заряженной сферы

теория по физике 🧲 электростатика

Любые заряженные тела создают вокруг себя электростатическое поле. Рассмотрим особенности электростатического поля, создаваемого точечным зарядом и заряженной сферой.

Видео:Поле заряженного кольцаСкачать

Электростатическое поле точечного заряда

Направление силовых линий электростатического поля точечного заряда

Положительный заряд +Q	Отрицательный заряд –Q
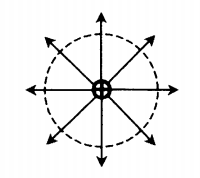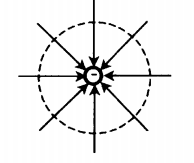У положительного заряда силовые линии направлены по радиальным линиям от заряда.	У отрицательного заряда силовые линии направлены по радиальным линиям к заряду.

Модуль напряженности не зависит от значения пробного заряда q₀:

E = F K q 0 . . = k Q q 0 r 2 q 0 . . = k Q r 2 . .

Модуль напряженности точечного заряда в вакууме:

Модуль напряженности точечного заряда в среде:

Сила Кулона:

Потенциал не зависит от значения пробного заряда q₀:

φ = W p q o . . = ± k Q q 0 r q 0 . . = ± k Q r . .

Потенциал точечного заряда в вакууме:

Потенциал точечного заряда в среде:

Внимание! Знак потенциала зависит только от знака заряда, создающего поле.

Эквипотенциальные поверхности для данного случая — концентрические сферы, центр которых совпадает с положением заряда.

Работа электрического поля по перемещению точечного заряда:

A 12 = ± q ( φ 1 − φ 2 )

Пример №1. Во сколько раз увеличится модуль напряженности электрического поля, созданного точечным зарядом Q в некоторой точке, при увеличении значения этого заряда в 5 раз? Модуль напряженности электрического поля, созданного точечным зарядом, определяется формулой:

Формула показывает, что модуль напряженности и электрический заряд — прямо пропорциональные величины. Следовательно, если заряд, который создает поле, увеличится в 5 раз, то модуль напряженности создаваемого поля тоже увеличится в 5 раз.

Видео:НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО ПОЛЯ суперпозиция полейСкачать

Электростатическое поле заряженной сферы

Направление силовых линий электростатического поля заряженной сферы:

Положительно заряженная сфера +Q	Отрицательно заряженная сфера –Q
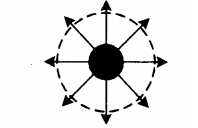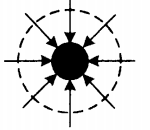У положительно заряженной сферы силовые линии — это радиальные линии, которые начинаются из этой сферы.	У отрицательно заряженной сферы силовые линии — это радиальные линии, которые заканчиваются в этой сфере.

Модуль напряженности электростатического поля заряженной сферы:

E = k Q r 2 . . = k Q ( R + a ) 2 . .

a — расстояние от поверхности сферы до изучаемой точки. r — расстояние от центра сферы до изучаемой точки.

Сила Кулона:

Потенциал:

φ = ± k Q r . . = ± φ = ± k Q R + a . .

Пример №2. Определить потенциал электростатического поля, создаваемого заряженной сферой радиусом 0,1 м, в точке, находящейся на расстоянии 0,2 м от этой сферы. Сфера заряжена положительна и имеет заряд, равный 6 нКл.

6 нКл = 6∙10 –9 Кл

Так как сфера заряжена положительно, то потенциал тоже положителен:

Два неподвижных точечных заряда действуют друг на друга с силами, модуль которых равен F. Чему станет равен модуль этих сил, если один заряд увеличить в n раз, другой заряд уменьшить в n раз, а расстояние между ними оставить прежним?

Алгоритм решения

Решение

Запишем исходные данные:

F K = k | q 1 | | q 2 | r 2 . .

Применим закон Кулона к парам зарядов. Закон Кулона для первой пары:

F K 1 = k | q 1 | | q 2 | r 2 . .

Закон Кулона для второй пары:

F K 2 = k | n q 1 | ∣ ∣ q 2 n . . ∣ ∣ r 2 . . = k | q 1 | | q 2 | r 2 . .

Коэффициент n сократился. Следовательно, силы, с которыми заряды взаимодействуют друг с другом, не изменятся:

После изменения зарядов модуль силы взаимодействия между ними останется равным F.

pазбирался: Алиса Никитина | обсудить разбор | оценить

В трёх вершинах квадрата размещены точечные заряды: +q, – «>– q, +q (q >0) (см. рисунок). Куда направлена кулоновская сила, действующая со стороны этих зарядов на точечный заряд +2q, находящийся в центре квадрата?

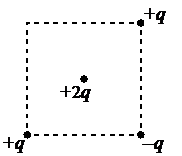
Алгоритм решения

Решение

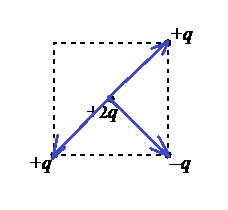
Сделаем чертеж. В центр помещен положительный заряд. Он будет отталкиваться от положительных зарядов и притягиваться к отрицательным:

Модули всех векторов сил, приложенных к центральному точечному заряду равны, так как модули точечных зарядов, расположенных в вершинах квадрата равны, и находятся они на одинаковом расстоянии от этого заряда.

Складывая векторы геометрически, мы увидим, что силы, с которыми заряд +2q отталкивается от точечных зарядов +q, компенсируют друг друга. Поэтому на заряд действует равнодействующая сила, равная силе, с которой он притягивается к отрицательному точечному заряду –q. Эта сила направлена в ту же сторону (к нижней правой вершине квадрата).

pазбирался: Алиса Никитина | обсудить разбор | оценить

На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка O – центр шарика, OA = 3R/4, OB = 3R, OC = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке C равен EC. Определите модуль напряжённости электростатического поля заряда Q в точке A и точке B?

Установите соответствие между физическими величинами и их значениями.

К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

🎥 Видео

Лекция 2-2 Потенциал - примерыСкачать

Электрическое поле/Напряженность и потенциал поля/Разность потенциалов/Работа поляСкачать

Урок 229. Работа электрического поля. Потенциал. Электрическое напряжениеСкачать

Физика 10 класс (Урок№27 - Напряжённость и потенциал электростатического поля.Разность потенциалов.)Скачать

Электрическое поле. Напряженность электрического поля. Силовые линии электрического поля. 10 класс.Скачать

Задача №2. Потенциал проводящей сферы.Скачать

Билет №04 "Потенциал электростатического поля"Скачать

Урок 218. Напряженность электрического поляСкачать

3.9Скачать

Напряжённость и потенциал электростатического поля. Разность потенциаловСкачать

Урок 234. Задачи на электрический потенциал - 2Скачать

Потенциал электростатического поля, разность потенциалов | Физика 10 класс #50 | ИнфоурокСкачать

Урок 235. Задачи на электрический потенциал - 3Скачать

3.1.5 Потенциал электростатического поляСкачать

Падение потенциала вдоль проводникаСкачать

Потенциал электрического поля. Практическая часть. 10 класс.Скачать