- 1. Как найти неизвестную сторону треугольника
- 2. Как узнать сторону прямоугольного треугольника
- 3. Формулы сторон равнобедренного треугольника
- 4. Найти длину высоты треугольника
- Формулы для нахождения высоты треугольника
- Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
- Примеры задач
- Как найти площадь треугольника
- По формуле Герона
- Через основание и высоту
- Через две стороны и угол
- Через сторону и два прилежащих угла
- Площадь прямоугольного треугольника
- Площадь равнобедренного треугольника через стороны
- Площадь равнобедренного треугольника через основание и угол
- Площадь равностороннего треугольника через стороны
- Площадь равностороннего треугольника через высоту
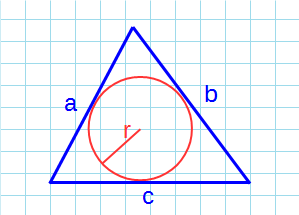
- Площадь равностороннего треугольника через радиус вписанной окружности
- Площадь равностороннего треугольника через радиус описанной окружности
- Площадь треугольника через радиус описанной окружности и три стороны
- Площадь треугольника через радиус вписанной окружности и три стороны
- 📹 Видео
Видео:№255. В равнобедренном треугольнике CDE с основанием СЕ проведена высота CF.Скачать

1. Как найти неизвестную сторону треугольника
Вычислить длину стороны треугольника: по стороне и двум углам или по двум сторонам и углу.
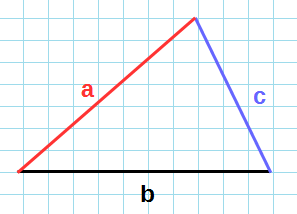
a , b , c — стороны произвольного треугольника
α , β , γ — противоположные углы
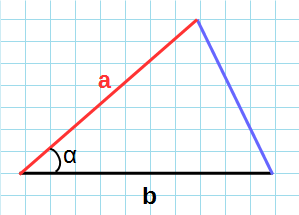
Формула длины через две стороны и угол (по теореме косинусов), ( a ):
* Внимательно , при подстановке в формулу, для тупого угла ( α >90), cos α принимает отрицательное значение
Формула длины через сторону и два угла (по теореме синусов), ( a):
Видео:№260. Высота, проведенная к основанию равнобедренного треугольника, равна 7,6 см, а боковая сторонаСкачать

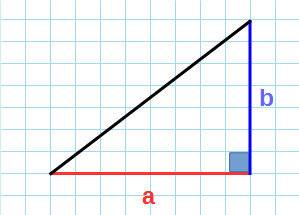
2. Как узнать сторону прямоугольного треугольника
Есть следующие формулы для определения катета или гипотенузы
a , b — катеты
c — гипотенуза
α , β — острые углы
Формулы для катета, ( a ):
Формулы для катета, ( b ):
Формулы для гипотенузы, ( c ):
Формулы сторон по теореме Пифагора, ( a , b ):
Видео:Формулы равностороннего треугольника #shortsСкачать

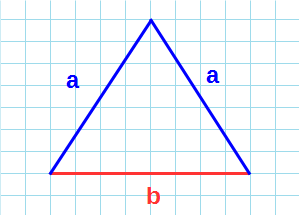
3. Формулы сторон равнобедренного треугольника
Вычислить длину неизвестной стороны через любые стороны и углы
b — сторона (основание)
a — равные стороны
α — углы при основании
β — угол образованный равными сторонами
Формулы длины стороны (основания), (b ):
Формулы длины равных сторон , (a):
Видео:№259. Угол, противолежащий основанию равнобедренного треугольника, равен 120°. Высота, проведеннаяСкачать

4. Найти длину высоты треугольника
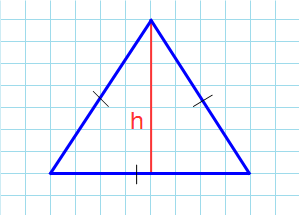
Высота— перпендикуляр выходящий из любой вершины треугольника, к противоположной стороне (или ее продолжению, для треугольника с тупым углом).
Высоты треугольника пересекаются в одной точке, которая называется — ортоцентр.

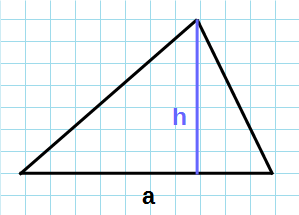
a — сторона, основание
b, c — стороны
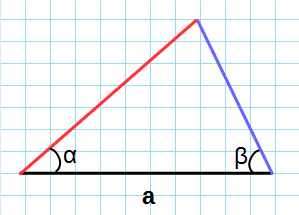
β , γ — углы при основании
p — полупериметр, p=(a+b+c)/2
R — радиус описанной окружности
S — площадь треугольника
Формула длины высоты через стороны, ( H ):
Формула длины высоты через сторону и угол, ( H ):
Формула длины высоты через сторону и площадь, ( H ):
Формула длины высоты через стороны и радиус, ( H ):
Видео:№107. В равнобедренном треугольнике основание в два раза меньше боковой стороны, а периметрСкачать

Формулы для нахождения высоты треугольника
В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.
Видео:№492. Найдите высоты треугольника со сторонами 10 см, 10 см и 12 см.Скачать

Нахождение высоты треугольника
Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.
Высота в разностороннем треугольнике
Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:
1. Через площадь и длину стороны
где S – площадь треугольника.
2. Через длины всех сторон
где p – это полупериметр треугольника, который рассчитывается так:
3. Через длину прилежащей стороны и синус угла
4. Через стороны и радиус описанной окружности
где R – радиус описанной окружности.
Высота в равнобедренном треугольнике
Длина высоты ha, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:
Высота в прямоугольном треугольнике
Высота, проведенная к гипотенузе, может быть найдена:
1. Через длины отрезков, образованных на гипотенузе
2. Через стороны треугольника
Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.
Высота в равностороннем треугольнике
Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:
Видео:№496. Основание D высоты CD треугольника ABC лежит на стороне АВ, причем AD=BC.Скачать

Примеры задач
Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.
Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:
Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.
Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:
Видео:№490. Найдите боковую сторону и площадь равнобедренного треугольника, если: а) основание равноСкачать
Как найти площадь треугольника
На данной странице калькулятор поможет рассчитать площадь треугольника онлайн. Для расчета задайте высоту, ширину и длину.
Треугольник – это многоугольник с тремя сторонами.
По формуле Герона
Формула Герона для нахождения площади треугольника:
Через основание и высоту
Формула нахождения площади треугольника с помощью половины его основания и высоту:
Через две стороны и угол
Формула нахождения площади треугольника через две стороны и угол между ними:
Через сторону и два прилежащих угла
Формула нахождения площади треугольника через сторону и два прилежащих к ней угла:
Площадь прямоугольного треугольника
Прямоугольный треугольник — треугольник у которого один из углов прямой, т.е. равен 90°.
Формула нахождения площади прямоугольного треугольника через катеты:
Площадь равнобедренного треугольника через стороны
Равнобедренный треугольник — треугольник, в котором две стороны равны. А значит, равны и два угла.
Формула нахождения площади равнобедренного треугольника через две стороны:
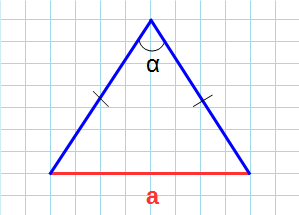
Площадь равнобедренного треугольника через основание и угол
Формула нахождения площади равнобедренного треугольника через основание и угол:
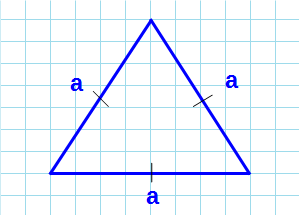
Площадь равностороннего треугольника через стороны
Равносторонний треугольник — треугольник, в котором все стороны равны, а каждый угол равен 60°.
Формула нахождения площади равностороннего треугольника через сторону:
Площадь равностороннего треугольника через высоту
Формула нахождения площади равностороннего треугольника через высоту:
Площадь равностороннего треугольника через радиус вписанной окружности
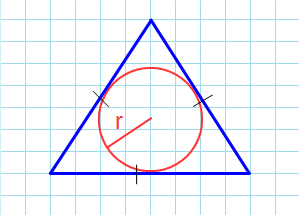
Формула нахождения пощади равностороннего треугольника через радиус вписанной окружности:
Площадь равностороннего треугольника через радиус описанной окружности
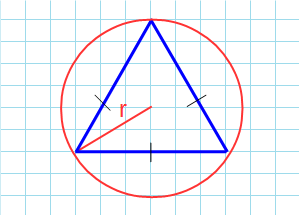
Формула нахождения пощади равностороннего треугольника через радиус описанной окружности:
Площадь треугольника через радиус описанной окружности и три стороны
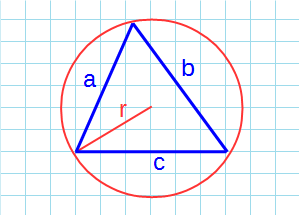
Формула нахождения пощади треугольника через радиус описанной окружности и три стороны:
Площадь треугольника через радиус вписанной окружности и три стороны
Формула нахождения пощади треугольника через радиус вписанной окружности и три стороны:
📹 Видео
№468. Пусть а — основание, h — высота, a S — площадь треугольника. Найдите:Скачать

№261. Докажите, что в равнобедренном треугольнике высоты, проведенные из вершин основания, равны.Скачать

Задача, которую исключили из экзамена в АмерикеСкачать

НАЙДИТЕ ВЫСОТУ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКАСкачать

Высоты треугольника.Скачать

7 класс, 17 урок, Медианы, биссектрисы и высоты треугольникаСкачать

Высота, биссектриса, медиана. 7 класс.Скачать

Площадь треугольника. Как найти площадь треугольника?Скачать

Вычисляем высоту через координаты вершин 1Скачать

7 класс, 18 урок, Свойства равнобедренного треугольникаСкачать

Почему площадь треугольника равна половине произведения основания на высотуСкачать
Определение натуральной величины треугольника АВС методом замены плоскостей проекцииСкачать