Сколько прямых параллельных данной плоскости можно провести в пространстве через точку не

Математика | 10 — 11 классы

Сколько прямых параллельных данной плоскости можно провести через данную точку не принадлежащей плоскости?

Через данную точку не принадлежащей плоскости можно провести бесконечное число прямых, параллельных плоскости.

Видео:10 класс, 4 урок, Параллельные прямые в пространствеСкачать

Даны три точки, не принадлежащие одной прямой?

Даны три точки, не принадлежащие одной прямой.

Докажите, что все прямые, пересекающие два из трёх отрезков, соединяющих данные точки, лежат в одной плоскости.

Видео:Параллельные прямые | Математика | TutorOnlineСкачать

Cколько плоскостей может проходить через 3 данные точки?

Cколько плоскостей может проходить через 3 данные точки?

При каком расположении трех точек через них можно провести бесконечно много плоскостей ?

Видео:Геометрия 10 класс (Урок№4 - Параллельность прямых, прямой и плоскости.)Скачать

Даны три точки, не принадлежащие одной прямой?

Даны три точки, не принадлежащие одной прямой.

Докажите, что все прямые, пересекающие два из трех отрезков, соединяющих данные точки, лежат в одной плоскости.

Видео:Геометрия 10 класс (Урок№6 - Параллельность плоскостей.)Скачать

Дана прямая, параллельная некоторой плоскости?

Дана прямая, параллельная некоторой плоскости.

Докажите что через любую точку этой плоскости проходит прямая, параллельная данной прямой.

Видео:Параллельность прямой и плоскости. 10 класс.Скачать

Лемма о параллельных прямых, пересекающих даную плоскость?

Лемма о параллельных прямых, пересекающих даную плоскость.

Видео:Параллельность прямых. 10 класс.Скачать

Сможете решить?

Нет? нужно описание?

* через всякую ли прямую можно провести плоскость параллельную данной плоскости?

(ответ : нет) нужно описание и чертеж!

Отмечу как лучший сразу!

Видео:Стереометрия 10 класс. Часть 1 | МатематикаСкачать

На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой?

На плоскости проведена прямая и отмечена точка, не лежащая на этой прямой.

Сколько прямых, параллельных данной, можно провести через эту точку?

Могут ли пересечься две прямые, перпендикулярные одной и той же прямой?

Видео:Параллельность прямых и плоскостей в пространстве. Практическая часть - решение задачи. 10 класс.Скачать

Укажите номер верного утверждения 1?

Укажите номер верного утверждения 1.

Существует точка плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной 2.

Через любые две различные точки плоскости можно провести прямую.

Видео:Перпендикулярность прямой и плоскости. 10 класс.Скачать

Стереометрия, 10 класс помогите?

Стереометрия, 10 класс помогите!

Из данных утверждений выберите верное : а) через точку, не принадлежащую двум данным плоскостям, можно провести прямую им параллельную ; б) через любую точку пространства проходит прямая параллельная данной плоскости и притом только одна ; в) если одна из двух параллельных плоскостей параллельна прямой, то и другая параллельная той же прямой ; г) утверждения а — в не верны.

Видео:Взаимное расположение прямых в пространстве. 10 класс.Скачать

Верны ли утверждения :1) Через точку, не принадлежащую данной плоскости, проходит единственнаяплоскость, параллельная данной?

Верны ли утверждения :

1) Через точку, не принадлежащую данной плоскости, проходит единственная

плоскость, параллельная данной.

2) Если две прямые, лежащие в одной плоскости, соответственно параллельны

двум прямым, лежащим в другой плоскости, то эти плоскости параллельны.

3) Существует бесконечно много прямых, параллельных данной плоскости и

проходящих через точку, не принадлежащую этой плоскости.

4) Если одна из двух данных плоскостей параллельна двум пересекающимся

прямым, лежащим в другой плоскости, то эти плоскости параллельны.

3. Докажите, что две плоскости, параллельные одной и той же третьей плоскости,

параллельны между собой.

4. Отрезки AB и CD лежат соответственно в параллельных плоскостях  и  (рис.

2). Как могут располагаться относительно друг друга прямые AC и BD?

На этой странице вы найдете ответ на вопрос Сколько прямых параллельных данной плоскости можно провести через данную точку не принадлежащей плоскости?. Вопрос соответствует категории Математика и уровню подготовки учащихся 10 — 11 классов классов. Если ответ полностью не удовлетворяет критериям поиска, ниже можно ознакомиться с вариантами ответов других посетителей страницы или обсудить с ними интересующую тему. Здесь также можно воспользоваться «умным поиском», который покажет аналогичные вопросы в этой категории. Если ни один из предложенных ответов не подходит, попробуйте самостоятельно сформулировать вопрос иначе, нажав кнопку вверху страницы.

Видео:10 класс, 10 урок, Параллельные плоскостиСкачать

Стереометрия. Страница 2

Видео:Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

1. Параллельность прямых в пространстве

Теорема. Через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.

Доказательство. Пусть b данная прямая и точка А, не лежащая на данной прямой. Проведем через точку А и прямую b плоскость α. А через точку А прямую a, параллельную прямой b. (Рис.1)

Допустим, что существует другая прямая а’, параллельная прямой b и проходящая через точку А. Тогда через них можно провести плоскость β. Отсюда следует, что через точку А и прямую b можно провести две плоскости. А это невозможно согласно теореме о единственности существования плоскости, проведеной через прямую и не лежащую на ней точку. Таким образом, плоскости α и β совпадают. А следовательно, согласно аксиоме, прямые а и a’ совпадают также.

5. Пример 1

Докажите, что если прямые АВ и CD скрещивающиеся, то прямые АС и BD тоже скрещиваются.

Доказательство:

Пусть даны две скрещивающиеся прямые АВ и CD. Проведем через прямую АВ и точку С плоскость α (Рис.5). Так как прямые АВ и CD скрещивающиеся, то прямая CD не лежит в плоскости α, а пересекает ее в одной точке С.

Отсюда следует, что точка D не принадлежит плоскости α. Она лежит вне ее.

Таким образом, если мы проведем прямую АС, то она полностью будет принадлежать плоскости α, так как две ее точки А и С принадлежат плоскости α.

А прямая BD не будет принадлежать плоскости α, так как точка D не принадлежит плоскости α. Прямая BD будет пересекать плоскость α в одной точке В.

Отсюда можно сделать вывод, что прямая АС не может пересекать прямую BD, так как прямая АС полностью принадлежит плоскости α. А прямая BD имеет только одну общую точку с плоскостью α, точку В. Но так как точка В не лежит на прямой АС, следовательно, прямые АС и BD не пересекаются. Они являются скрещивающимися.

Рис.5 Задача. Докажите, что если прямые АВ и CD скрещивающиеся.

Пример 2

Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем плоскость α через точки A, D, C и плосксоть α’ через точки А, В, С (Рис.6). Точки P, S, F, E являются серединами отрезков AB, BC, AD и CD соответственно. Необходимо доказать, что прямая PS параллельна прямой FE.

Рассмотрим треугольник АВС. Он полностью лежит в плоскости α’, так как три его вершины лежат в данной плоскости по построению. Отрезок PS представляет собой среднюю линию треугольника, которая параллельна АС.

Теперь рассмотрим треугольник АСD. Он полностью лежит в плоскости α, так как три его вершины лежат в данной плоскости по построению. Отрезок FE представляет собой среднюю линию треугольника, которая также параллельна АС.

Отсюда можно сделать вывод: если две прямые PS и FE параллельны третьей прямой АС, то они параллельны и между собой. И равны половине основанию АС. Таким образом, PSEF представляет собой параллелограмм.

Рис.6 Задача. Точки А, В, С, D не лежат в одной плоскости.

Пример 3

Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины отрезков АВ и ВС, АС и BD, AD и BC пересекаются в одной точке.

Доказательство:

Пусть даны четыре точки А, В, С, D, которые не лежат в одной плоскости. Проведем отрезки EP, VS, FT, которые соединят середины сторон AB и CD, BC и AD, AC и BD соответственно (Рис.7).

Из предыдущей задачи нам известно, что четырехугольник EVPS, вершины которого являются серединами отрезков АВ, ВС, СD и AD, есть параллелограмм, у которого EP и VS диагонали. Эти диагонали пересекаются в точке О и делятся этой точкой пополам.

Теперь рассмотрим четырехугольник VTSF. Данный четырехугольник также является параллелограммом, так как его вершины — это середины отрезков BC, BD, AC и AD. А его диагонали VS и FT пересекаются в точке О и делятся этой точкой пополам.

Так как у отрезка VS середина одна, т.е. точка О, то все три диагонали EP, VS и FT пересекаются в этой точке.

Рис.7 Задача. Даны четыре точки А, В, С, D, не лежащие в одной плоскости.

Пример 4

Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость α по параллельным прямым, то прямая а параллельна плоскости α.

Доказательство:

Пусть даны две плоскости β и γ, пересекающиеся по прямой а (Рис.8). Эти плоскости пересекают плоскость α по параллельным прямым b и с. Необходимо доказать, что прямая а параллельна плоскости α.

Прямая b — это множество точек, которые одновременно принадлежат плоскостям α и γ. Прямая с — это множество точек, которые одновременно принадлежат плоскостям α и β. Так как прямые b и с параллельны, то на этих прямых нет ни одной точки, которая одновременно принадлежала бы трем плоскостям.

Прямая а — это множество точек, которые принадлежат двум плоскостям β и γ. Допустим, что она пересекает плоскость α. Тогда на ней должна быть точка, которая принадлежала бы одновременно трем плоскостям. А следовательно, она одновременно лежала бы на прямых b и с. Но это противоречит условию задачи, так как прямые b и с не пересекаются. Следовательно, прямая а параллельна прямым b и с. А отсюда следует, что она параллельна плоскости α.

Рис.8 Задача. Докажите, что если две плоскости, пересекающиеся по прямой а.

Пример 5

Докажите, что если четыре прямые, проходящие через точку О, пересекают плоскость α в вершинах параллелограмма, то они пересекают любую плоскость, параллельную α и не проходящую через точку О, тоже в вершинах параллелограмма.

Доказательство:

Пусть даны четыре прямые, проходящие через точку О, ОА, ОВ, ОС и OD (Рис.9). Они пересекают плоскость α в точках А, В, С и D соответственно. Проведем плоскость α’, параллельную плоскости α. Тогда прямые ОА, ОВ, ОС и OD пересекут плоскость α’ в точках A’B’C’D’.

Проведем плоскость β через точки А, В, A’, B’. Тогда прямые АВ и A’B’ не пересекаются, так как это прямые пересечения двух параллельных плоскостей α и α’ с секущей плоскостью β.

Отсюда следует, что прямые ВС и В’С’, CD и C’D’, AD и A’D’ параллельны. А так как АВ параллельна CD, а ВС параллельна AD, то следовательно, А’В’ параллельна C’D’, а В’С’ параллельна A’D’.

Таким образом, A’B’C’D’ также является параллелограммом.

Рис.9 Задача. Докажите, что если четыре прямые, проходящие через точку А.

Видео:ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ и ПЛОСКОСТИ 10 11 класс стереометрияСкачать

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Две прямые в пространстве называются параллельными , если они лежат в одной плоскости и не пересекаются. Прямые, которые не пересекаются и не лежат в одной плоскости называются скрещивающимися. Прямая и плоскость в пространстве называются параллельными, если они не пересекаются.

Прямая параллельна плоскости, если она параллельна какой-нибудь прямой, лежащей в этой плоскости.

Две плоскости называются параллельными, если они не пересекаются.

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны. Через точку, не лежащую в данной плоскости, можно провести параллельную плоскость, и притом только одну.

, так как

Отрезки параллельных прямых между параллельными плоскостями равны.

= =

Прямые в пространстве называются перпендикулярными, если они пересекаются под прямым углом. Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой в плоскости, проходящей через точку их пересечения.

Прямая, пересекающая плоскость, перпендикулярна плоскости, если она перпендикулярна двум прямым в плоскости, проходящим через точку их пересечения.

.

Через каждую точку плоскости можно провести перпендикулярную ей прямую, и только одну. Все прямые, перпендикулярные данной плоскости, параллельны.

Перпендикуляр, опущенный из данной точки на данную плоскость, — это отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, которая перпендикулярна плоскости. Основание перпендикуляра — это его конец, лежащий в плоскости.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного от этой точки на плоскость.

Наклонная, проведенная из данной точки к данной плоскости, — это любой отрезок, соединяющий данную точку с точкой плоскости, который не является перпендикуляром к плоскости. Конец отрезка, который лежит в плоскости, — это основание наклонной. Проекция наклонной — это отрезок, который соединяет основания перпендикуляра (точку С) и наклонной (точку А).

Если прямая, проведённая на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной. И обратно, если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

Две пересекающиеся плоскости называются перпендикулярными, если плоскость, перпендикулярная прямой их пересечения, пересекает данные плоскости по перпендикулярным прямым.

Так как , то .

Поделись с друзьями в социальных сетях:

📹 Видео

Параллельность прямой к плоскостиСкачать

10 класс, 6 урок, Параллельность прямой и плоскостиСкачать

Построение параллельной плоскости на расстояние 30 мм.Скачать

Урок ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕСкачать

Главная > Учебные материалы > Математика: Стереометрия. Страница 2 1.Параллельность прямых в пространстве. 2.Признак параллельности прямых. 3.Признак параллельности плоскостей. 4.Свойства параллельных плоскостей. 5.Примеры.

1 2 3 4 5 6 7 8

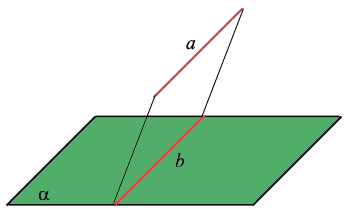
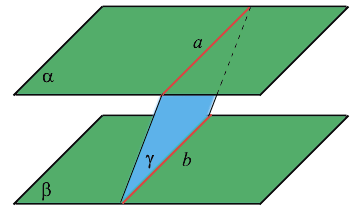
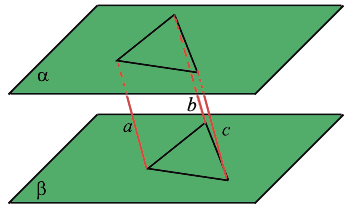
Рис. 1 Параллельность прямых в пространстве. Видео:Построение прямой, параллельной даннойСкачать 2.Признак параллельности прямых Теорема. Две прямые, параллельные третьей прямой, параллельны. Доказательство. Пусть прямые а и b лежат в разных плоскостях и параллельны прямой с. Доказать, что прямые а и b параллельны между собой. (Рис.2) Проведем через прямую a и c плоскость α. Через прямые b и c плоскость β. Прямая с — прямая пересечения плоскостей α и β. Отметим на прямой а точку А. Проведем через точку А и прямую b плоскость γ. Тогда плоскость γ будет пересекать плоскость α по прямой а’. Прямая a’ либо паралельна прямой c, либо ее пересекает. Допустим прямая а’ пересекает прямую с. Тогда эта точка пересечения принадлежит плоскости β, т.к. прямая с принадлежит двум плоскостям α и β. А т.к. прямая а’ полностью принадлежит плоскости γ, а прямая b есть прямая пересечения плоскостей γ и β, то это означает, что она пересекает и прямую b. А это означает, что прямые b и c пересекаются, т.к. прямая a’ пересекает плоскость β только в одной точке, которая должна принадлежать двум прямым b и с. А это противоречит условию. Следовательно прямая a’ не пересекает прямую с. Она ей параллельна. Согласно аксиоме, на плоскости α, через точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной. И эта прямая а. Т.е. прямые а и а’ совпадают. Это значит, что прямые а и b параллельны. Рис.2 Признак параллельности прямых Видео:Видеоурок "Параллельные прямые в пространстве"Скачать 3. Признак параллельности плоскостей Теорема: если две пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости, то эти плоскости параллельны. Доказательство. Пусть α и β данные плоскости. Прямая а параллельна прямой а 1 . Прямая b параллельна b 1 (Рис.3). Допустим, что плоскости α и β пересекаются по прямой с. Тогда прямая с должна пересекать, как минимум, одну из прямых на каждой плоскости. Пусть это будут прямые а и а 1 . Т.к. прямые а и а 1 параллельны, следовательно они пересекают прямую с в разных точках Е и Е 1 . Проведем через две параллельные прямые а и а 1 плоскость γ. Тогда точки Е и Е 1 , которые лежат на прямой с, будут принадлежать плоскости γ. Следовательно, прямая с полностью принадлежит плоскости γ. Отсюда следует, что: а ∈ α, γ. а 1 ∈ β, γ. с ∈ α, β,γ т.е. плоскости α и γ пересекаются по двум прямым а и с, а плоскости β и γ пересекаются по прямым а 1 и с. Рис. 3 Признак параллельности плоскостей. Согласно аксиоме стереометрии, это невозможно, т.к. две плоскости могут пересекаться только по одной прямой. И следовательно, наше предположение неверно. Плоскости α и β не пересекаются, они параллельны. Видео:Параллельность прямых. Практическая часть. 10 класс.Скачать 4. Свойства параллельных плоскостей Теорема: Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Доказательство. Пусть даны две параллельные плоскости α и β (Рис.4). Плоскость γ пересекает их по прямым а и b. Допустим, что прямые пересечения плоскостей пересекаются. Это прямые а и b’. Прямая а — это множество точек, принадлежащих плоскостям α и γ. А так как прямая b’ представляет собой множество точек, пренадлежащих двум плоскостям β и γ, то отсюда следует, что существует точка пересечения прямых а и b’, которая принадлежит плоскости α. И следовательно, плоскости α и β имеют общую точку. А это противоречит условию, т.к. плоскости α и β не пересекаются, они параллельны. Следовательно, прямые а и b лежат в одной плоскости и не пересекаются. Т.е. они тоже параллельны. Рис. 4 Свойства параллельных плоскостей.
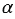
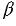
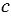