- Ваш ответ
- решение вопроса
- Похожие вопросы
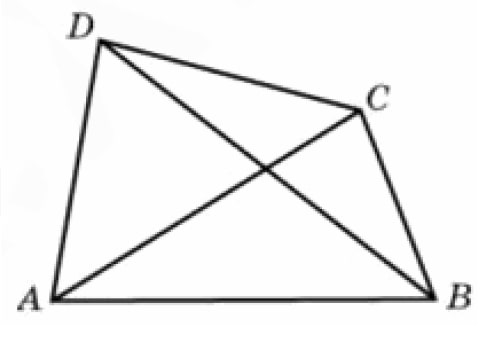
- Решение №636 Диагонали четырехугольника равны 7 и 10.
- В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. — презентация
- Похожие презентации
- Презентация на тему: » В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.» — Транскрипт:
- 🎦 Видео
Видео:ЕГЭ Математика Задание 6#27845Скачать

Ваш ответ
Видео:Найти периметр четырехугольника, вершины которого лежат на серединах сторон другого четырехугольникаСкачать

решение вопроса
Видео:Диагонали четырехугольника равны 4 и 5.Скачать

Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,701
- разное 16,822
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Геометрия Найдите диагональ четырехугольника, если его периметр равен 80 см, а периметрыСкачать

Решение №636 Диагонали четырехугольника равны 7 и 10.
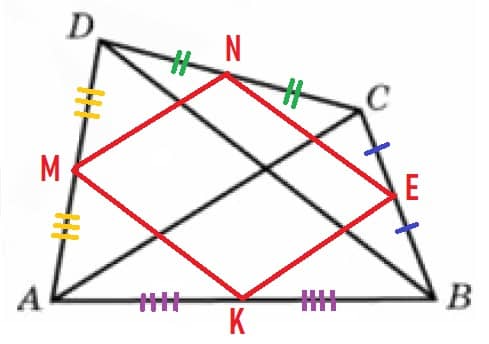
Диагонали четырехугольника равны 7 и 10. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Стороны четырёхугольника MNEK, являются средними линиями соответствующих треугольников и равны половине оснований Δ:
MN = AC/2= 7/2 = 3,5
KE = AC/2= 7/2 = 3,5
MK = DB/2= 10/2 = 5
NE = DB/2= 10/2 = 5
Периметр равен:
P = MN + KE + MK + NE = 3,5 + 3,5 + 5 + 5 = 17
Ответ: 17.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.5 / 5. Количество оценок: 2
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время
В отзыве оставляйте контакт для связи, если хотите, что бы я вам ответил.
Видео:№406. Найдите периметр ромба ABCD, в котором ∠B=60°, АС = 10,5 см.Скачать

В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. — презентация
Презентация была опубликована 8 лет назад пользователемschool4.vx6.ru
Похожие презентации
Видео:№502. Высоты параллелограмма равны 5 см и 4 см, а периметр равен 42 см. Найдите площадь параллелограСкачать

Презентация на тему: » В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.» — Транскрипт:
1 В А D С Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника. E F Q Р 4 5 Применим свойство средней линии треугольника. QP = 5 : 2 = 2,5 QP – средняя линия треугольника ADC EF = 5 : 2 = 2,5 EF – средняя линия треугольника ABC PF = 4 : 2 = 2 PF – средняя линия треугольника DBC QE = 4 : 2 = 2 QE – средняя линия треугольника DBA P = (2,5+2)*2 = х 1 0 х В 4 9
2 Открытый банк заданий по математике b a (a+b) : 2
3 В А D С В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию F E O OBE – равнобедренный BE = OE OFC – равнобедренный FO = FC DC = 2FO AB = 2OE DC + AB = 2FO + 2OE = 2 FE = 24 (DC + AB) : 2 = 24 : 2 = 12 Средняя линия трапеции равна полусумме оснований+2. 3 х 1 0 х В 4 1 2
4 В А D С Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции F E EL = 1,5 FL = 1 EF = 0,5–3 2L Применим свойство средней линии треугольника. FL = 2 : 2 = 1 FL – средняя линия треугольника BDC EL = 3 : 2 = 1,5 EL – средняя линия треугольника ABC F – середина DB по условию L – середина СВ по теореме Фалеса 3. 3 х 1 0 х В 4 0, 5
5 В А D С Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции. L E 2F EL = = 7 EL – средняя линия треугольника ADC 4. x x+2 Это значит, что один из отрезков НА 2 больше другого. x + x + 2 = 12 x = 5 AB = 7 * 2 = 14 3 х 1 0 х В 4 1 4
6 В А D С Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции. F E 5. x x+4 x + x + 4 = 14 2x = 10 Средняя линия трапеции равна полусумме оснований * 2 x = 5 AB = 9 3 х 1 0 х В 4 9
7 Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции А D С F E Средняя линия трапеции равна полусумме оснований. * 2 x x x B 2x 2x + x + x = 80 4 x = 80 x = 20 3 х 1 0 х В Периметр равен 80
8 Основания трапеции относятся как 2 : 3, а средняя линия равна 5. Найдите меньшее основание.7. В А D С F E 2x2x2x2x 3x3x3x3x 2x + 3x = 10 5x = 10 Средняя линия трапеции равна полусумме оснований * 2 x = 2 DC = 4 3 х 1 0 х В 4 45 Пусть х – 1 часть
9 Периметр трапеции равен 50, а сумма непараллельных сторон равна 20. Найдите среднюю линию трапеции.8. В А D С F E Сумма непараллельных сторон равна 20. Значит, можно найти сумму параллельных сторон. 3 х 1 0 х В – 20 = 30 сумма параллельных сторон, т.е. сумма оснований30
10 Основания равнобедренной трапеции равны 15 и 9, один из углов равен Найдите высоту трапеции.9. А DС В равнобедренной трапеции построим две высоты. Получим два равных прямоугольных треугольника и прямоугольник. 3 х 1 0 х В 4 3 F 45 0 E AF = (15 – 9) : 2 = 3 B 3 Треугольник прямоугольний и равнобедренный
11 В А D С Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции E 10 F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник – 4 = 6 отрезок EF 6 Средняя линия трапеции равна полусумме оснований 3 х 1 0 х В = 14
12 В А DС Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции. E P ADE = P ABCD = DC + CB + BE + EA + AD = DE DE + EA + AD =15 = 23 3 х 1 0 х В 4 2 3
13 В равнобедренной трапеции основания равны 12 и 27, острый угол равен Найдите ее периметр. 12. В А D С 12 E F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник. (27 – 12) : 2 = 7,5 отрезки AF, BE 3 х 1 0 х В ,5
14 В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними Найдите меньшее основание В А D С E F В равнобедренной трапеции построим вторую высоту. Получим два равных прямоугольных треугольника и прямоугольник. 25 – (5+5) = 15 отрезки EF и DC 3 х 1 0 х В
15 Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из ее диагоналей.14. В А D С E F L EL = 10 : 2 = 5 EL – средняя линия треугольника ADB FL = 4 : 2 = 2 FL – средняя линия треугольника DBC 3 х 1 0 х В
16 Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции В А D С E F 3 х 1 0 х В Средняя линия трапеции равна полусумме оснований.1828 * 2
17 Найдите среднюю линию трапеции, если ее основания равны 30 и В А D С E F 3 х 1 0 х В Средняя линия трапеции равна полусумме оснований.
18 Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 50 0 ? Ответ дайте в градусах В А DС x x+50 Это значит, что один из углов НА 50 0 больше другого. В равнобедренной трапеции углы при основании равны x x+50 x + x + 50 =180 сумма односторонних углов при параллельных прямых равна 180 0, AB II DC, AD — секущая 2x + 2(x + 50) =360 сумма углов четырехугольника способ 2 способ x = 65 Тогда тупой уго трапеции равен = х 1 0 х В
🎦 Видео
ЕГЭ 2017 | Задание 3 | Диагонали четырехугольника равны ... ✘ Школа ПифагораСкачать

Четырехугольник ABCD. Свойства. Диагональ. Геометрия 8 класс. Глава 5.Скачать
Сложные примеры с поиском периметра 3 задание проф. ЕГЭ по математикеСкачать

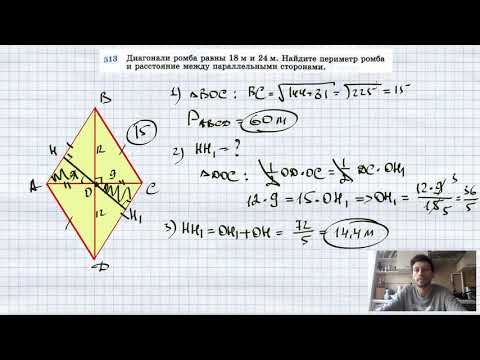
№513. Диагонали ромба равны 18 м и 24 м. Найдите периметр ромба и расстояние между параллельными стоСкачать
38. Геометрия на ЕГЭ по математике. Задача на тему "Средняя линия треугольника"Скачать

8 задание ЕГЭ по математике профильному.Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объемСкачать

№403. В прямоугольнике ABCD диагонали пересекаются в точке О. Найдите периметрСкачать

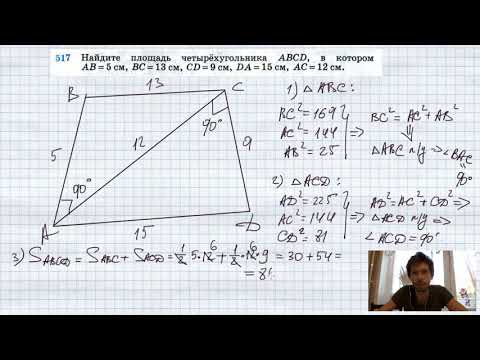
№517. Найдите площадь четырехугольника ABCD, в котором АВ = 5 см, ВС = 13 см, CD = 9 см, DA =15 смСкачать
Геометрия Найдите периметр ромба, диагонали которого равны 24 см и 32 смСкачать

Периметр прямоугольника. Как найти периметр прямоугольника?Скачать

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

8 класс, 3 урок, ЧетырехугольникСкачать

Задание 3 ЕГЭ по математике. Урок 46Скачать

8 класс, 4 урок, ПараллелограммСкачать