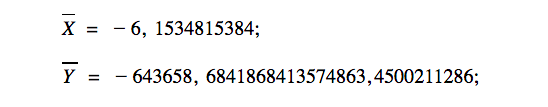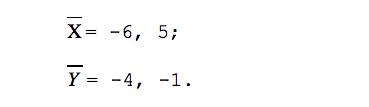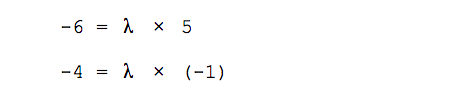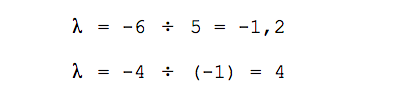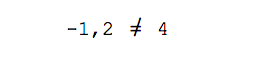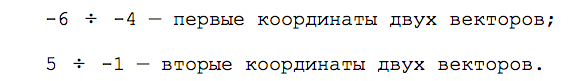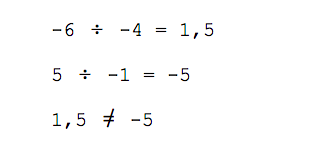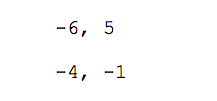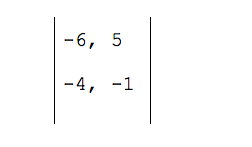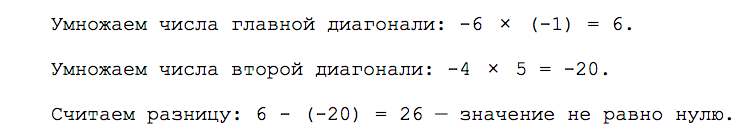Построить три неколлинеарных вектора

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы напомним основные определения и рассмотрим типовые задачи на компланарные векторы.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

Видео:№776. Начертите два неколлинеарных вектора х и у и постройте векторы: a) x+2y; б) ½y + х; в) 3x+½yСкачать

Векторы: третий уровень сложности

Знакомимся с коллинеарностью.

Для большинства людей искусственный интеллект — это нечто сложное и таинственное. А для математиков это синоним фразы «перемножение матриц». С точки зрения человека, который владеет линейной алгеброй, в искусственном интеллекте нет ничего загадочного.

Мы хотим, чтобы вы тоже смогли понять искусственный интеллект на уровне математики. Для этого у нас идёт цикл статей про линейную алгебру:

Сама тема несложная, но конкретно этот шаг вам ничего не даст в практическом смысле. Но если вам хватит терпения, на базе этих знаний мы уже перейдём к матрицам.

Видео:№778. Начертите попарно неколлинеарные векторы а, b и c. Постройте векторы:Скачать

Что за коллинеарность

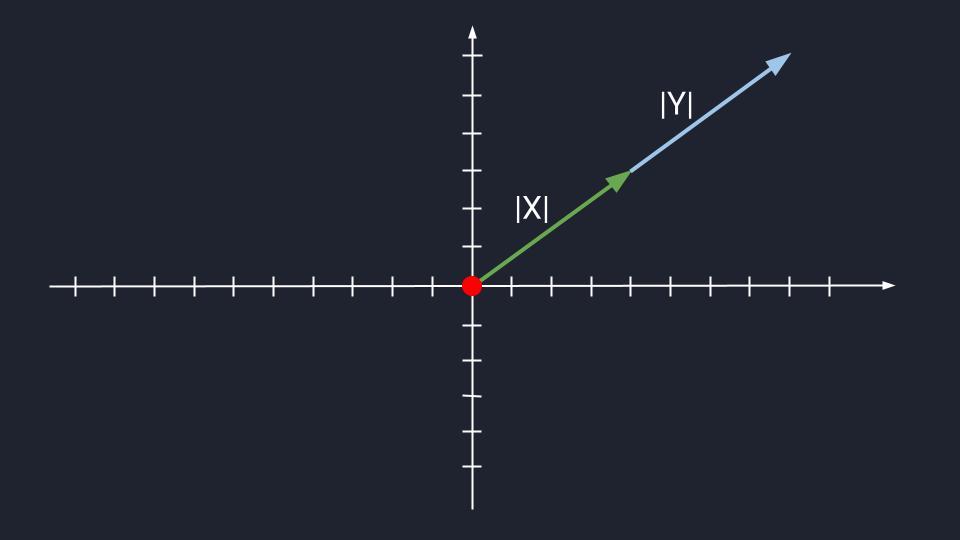
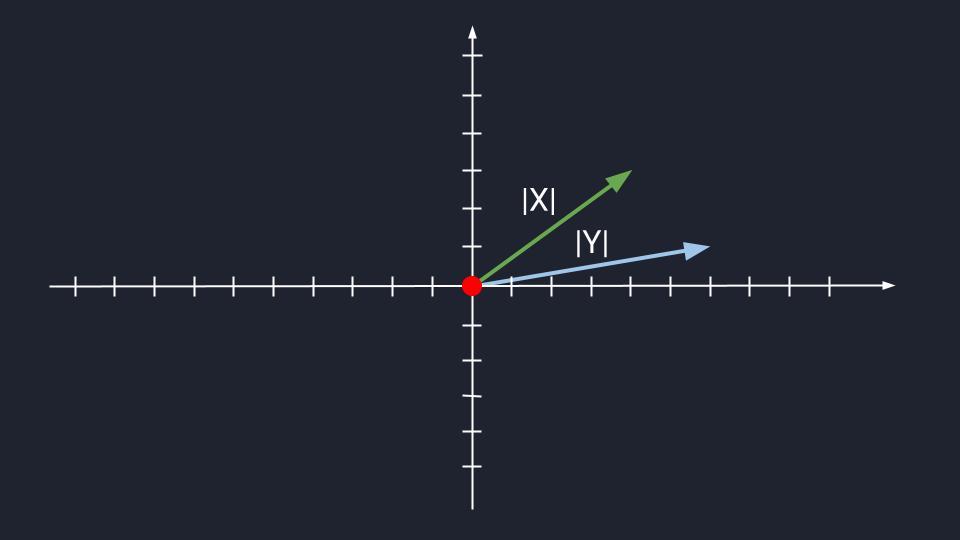
Представьте два вектора, которые находятся в одной плоскости и располагаются параллельно друг другу. При этом у них может быть разная длина. Такое расположение делает связку векторов коллинеарными, или, по-простому, линейно зависимыми.

И наоборот: если вектора находятся в одной плоскости и располагаются не параллельно друг относительно друга, то их считают линейно независимыми — неколлинеарными. Пока что ничего сложного.

Коллинеарные векторы Неколлинеарные векторы

Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Сложение коллинеарных и неколлинеарных векторов

Очевидно, что сложить два коллинеарных вектора очень легко: откладываем второй вектор от начала первого, получится новый вектор. Он будет коллинеарным своим слагаемым, они все будут лежать, грубо говоря, на одной линии.

Можно представить, что вы идёте прямо: каждый ваш шаг — это вектор. Каждый новый шаг — новый вектор. Но если все их сложить, получится один большой прямой вектор длиной как все ваши шаги.

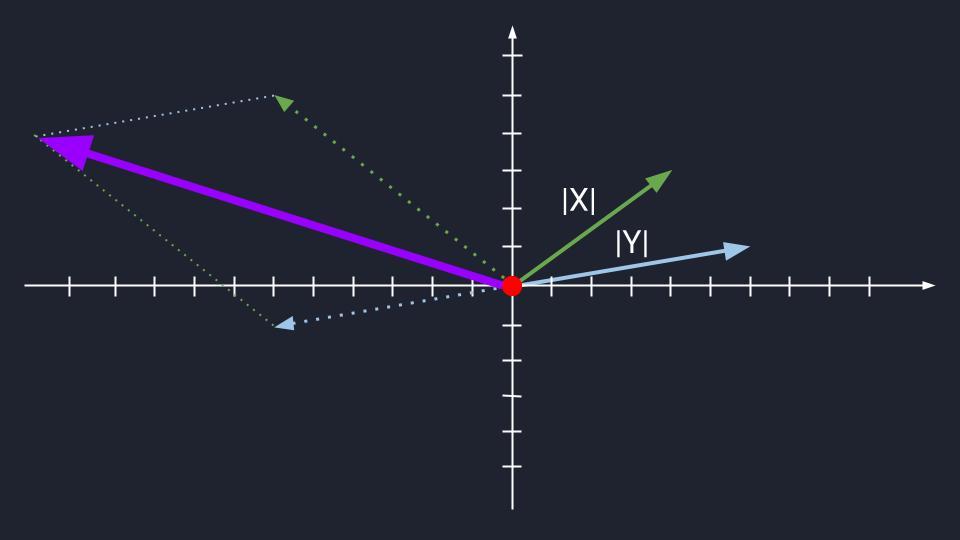
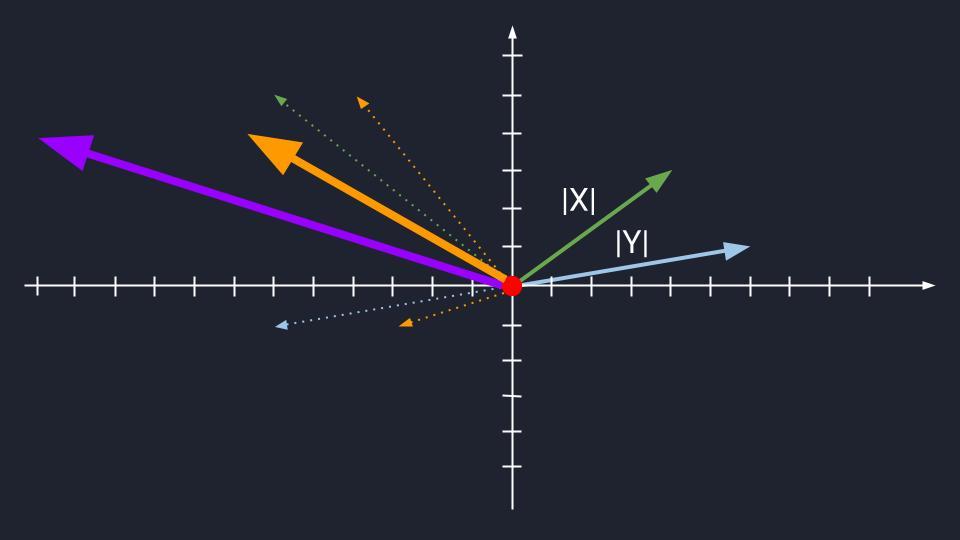
Теперь попробуем сложить пару неколлинеарных векторов. Это как если бы мы сначала сделали шаг немного правее, а потом сделали бы шаг влево. Шага два, но если соединить начало и конец пути, он не будет совпадать с траекториями наших шагов. Появится какой-то новый вектор, с новым направлением, и он будет неколлинеарным по отношению к своим слагаемым.

Также пару неколлинеарных векторов из одной плоскости можно растянуть и развернуть в пространстве. Если их сложить, также появится новый вектор.

У математиков такой вектор называют базисом. Когда базис находится на плоскости или в пространстве, то он может единственным образом превращаться обратно в пару неколлинеарных векторов, которые его сформировали.

Правило работает, когда мы масштабируем и меняем расположение векторов в пространстве. Если мы изменим направление исходных векторов, то получим новый базис.

Базис — понятие из высшей математики, поэтому, если сейчас сложно, не отчаивайтесь. Студенты-математики когда-то тоже отчаивались.

Мы изменили пару неколлинеарных векторов и сформировали из них базис — получили новый фиолетовый вектор с собственной системой координат Теперь мы изменили исходные неколлинеарные векторы и получили новый базис — это оранжевый вектор

Видео:№754. Начертите попарно неколлинеарные векторы х, у , z и постройте векторы x+у, x+z, z+y.Скачать

Как определять неколлинеарность

Когда мы работаем с короткими векторами, всё очевидно: нарисовали систему координат, отложили на ней векторы, они либо совпали, либо не совпали. Если совпали — коллинеарные, если нет — неколлинеарные.

А теперь представьте, что вектора настолько огромные, что мы физически не можем их нарисовать и сопоставить. Например,

Как такое нарисовать? Как проверить коллинеарность? Вот тут начинается магия алгебры.

Есть три способа проверки линейной зависимости векторов. Для простоты вычислений проверим эти три способа на вот этих всё ещё простых векторах:

По этим координатам ответим на два вопроса: являются ли предложенные вектора линейно зависимыми (то есть коллинеарными) и можно ли их раскладывать по базису.

Первый способ. Запишем простую систему уравнений: возьмём первую координату каждого вектора и приравняем её ко второй координате каждого вектора, умноженной на неизвестное число λ. Вычислим λ и сравним результаты.

👉 Знак λ здесь по традиции и для удобства. На самом деле это просто некое неизвестное число. Вместо этой буквы могли быть X, Y, Z или N, но так как у нас вектора уже называются X и Y, а N в математике используется для других целей, возьмём λ — это греческая буква «лямбда», давний предок нашей русской буквы «Л».

Составляем систему уравнений:

Вычисляем значение λ:

Сравниваем результат и делаем вывод:

Мы получили разное значение для неизвестного числа λ и поэтому наши векторы будут считаться линейно независимыми. Из них можно получить базис.

Если бы значение λ совпало, то мы бы имели дело с линейно зависимыми векторами.

Второй способ. Проверяем координаты векторов на пропорциональность: берём первую координату первого вектора, делим её на первую координату второго вектора. Повторяем это же действие со вторыми координатами: берём вторую координату первого вектора и делим её на вторую координату второго вектора.

Получаем такую пропорцию:

Считаем значение и сравниваем результат:

Равенство не выполняется, и поэтому между векторами нет зависимости.

Третий способ. Используем четыре элемента наших координат для поиска определителя — скалярной величины, с которой мы подробно познакомимся в следующих статьях во время решения матричных уравнений. Сейчас нам не нужны подробности, и для проверки линейной зависимости достаточно формулы.

Записываем в две строки координаты наших векторов:

Переводим координаты векторов в определитель — добавляем с двух сторон вертикальную черту и получаем простую квадратную матрицу размером 2 на 2:

В полученной матрице две диагонали. Числа −6 и −1 образуют главную диагональ; числа −4 и 5 — вторую диагональ. Чтобы найти определитель, нам нужно умножить числа главной и второй диагонали, а затем вычесть их разницу.

Если из координат вектора мы получили определитель и он не равен нулю, то векторы считаются линейно независимыми и подходят для разложения по базису.

И наоборот: нулевой определитель указывает на линейную зависимость векторов.

Видео:10 класс, 45 урок, Разложение вектора по трем некомпланарным векторамСкачать

Что из этого нужно запомнить

• С точки зрения векторов важно, они сонаправленные или нет. По-другому — они коллинеарны или нет.
• Коллинеарность влияет на то, что можно делать с этими векторами. Например, неколлинеарные векторы можно разложить по базису.
• Базис — это вектор, который можно разложить на те самые неколлинеарные векторы.
• Коллинеарность легко проверяется через уравнения. Строить векторы на координатной плоскости необязательно.

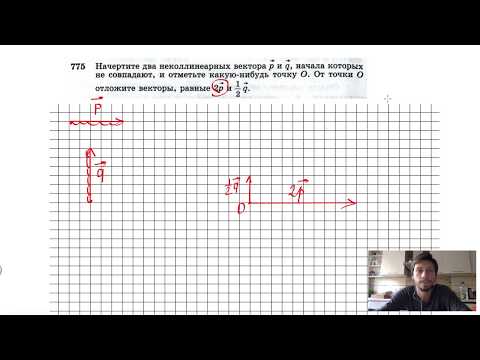
Видео:№777. Начертите два неколлинеарных вектора р и q , начала которых не совпадают.Скачать

Что дальше

Следующий шаг — матрицы. Это те самые, которые лежат в основе всех нейронок и искусственного интеллекта. Матрица — это таблица чисел, с которыми можно проводить различные вычисления.

Видео:№756. Начертите попарно неколлинеарные векторы х , у , z и постройте векторыСкачать

Даны три неколлинеарных вектора a, b, c Начертите, пожалуйста, как построить : а)А + б — с б) — 2а — б + 3с в) а + 2б — 1 / 2с?

Геометрия | 5 — 9 классы

Даны три неколлинеарных вектора a, b, c Начертите, пожалуйста, как построить : а)А + б — с б) — 2а — б + 3с в) а + 2б — 1 / 2с.

Я посчитала токо что.

Видео:№775. Начертите два неколлинеарных вектора р и q , начала которых не совпадаютСкачать

Даны 2 неколлинеарных вектора а и b построить 2b — a?

Даны 2 неколлинеарных вектора а и b построить 2b — a.

Видео:№741. Начертите два неколлинеарных вектора а и b. Изобразите несколько векторов:Скачать

Даны три неколлинеарных вектора a — &gt ; b — &gt ; c — &gt ; ?

Даны три неколлинеарных вектора a — &gt ; b — &gt ; c — &gt ; .

Постройте вектор равный их сумме.

Видео:9 класс, 1 урок, Разложение вектора по двум неколлинеарным векторамСкачать

Даны неколлинеарные векторы a и b постройте вектор с если с = a — 3b?

Даны неколлинеарные векторы a и b постройте вектор с если с = a — 3b.

Видео:Вычитание векторов. 9 класс.Скачать

Начертить два неколлинеарных вектора a и b, нужно построить вектор С если : 1)с = 2а + 3б 2)с = а — 3б?

Начертить два неколлинеарных вектора a и b, нужно построить вектор С если : 1)с = 2а + 3б 2)с = а — 3б.

Видео:Коллинеарные векторы.Скачать

СРОООЧНО?

№1Начертите попарно неколлинеарные векторы : х, у, z и постройте векторы х — у , z — y , x — z, — — х, — — у, — — z.

( и как понять попарно неколлинеарные векторы ) №2 Начертите попарно неколлинеарные векторы х, у , z, и постройте векторы х + у, х + z, z + y РЕШИТЕ ПОЖАЛУСТА НА ЛИСТОЧКЕ И ДОБАВЬТЕ ВО ВЛОЖЕНИЯ!

КТО СДЕЛАЕТ ЭТО ЗАДАНИЕ ТОМУ БУДУ ОЧЕНЬ БЛАГОДАРНА.

Видео:Разложение вектора на неколлинеарные вектора.Скачать

ПОЖАЛУЙСТА ПОМОГИТЕ ЗАВТРА КОНТРОЛЬНАЯ?

ПОЖАЛУЙСТА ПОМОГИТЕ ЗАВТРА КОНТРОЛЬНАЯ!

1) начертите пять попарно неколлинеарных векторов а б с д е построейте вектор а + в + с + д + е 2) упростите выражение : PG + EF + AE + GA 3)Дан прямоугольный треугольник АВС с гипотенузой АВ.

Постройте вектор m = ВА + ВС — СА и найдите |m| если ВС = 9 см.

Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать

Начертите попарно три неколлинеарные векторы a, b и c?

Начертите попарно три неколлинеарные векторы a, b и c.

Постройте вектор p.

Видео:Геометрия 9 класс (Урок№7 - Разложение вектора по двум неколлинеарным векторам. Координаты вектора.)Скачать

Начертите неколлинеарные векторы а и в с разными началами и постройте их сумму по правилу параллелограмма?

Начертите неколлинеарные векторы а и в с разными началами и постройте их сумму по правилу параллелограмма.

Видео:Координаты вектора. 9 класс.Скачать

Начертите неколлинеарные векторы m и n и постройте вектор равный 3m — 1 / 2n?

Начертите неколлинеарные векторы m и n и постройте вектор равный 3m — 1 / 2n.

Видео:ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать

Начертите неколлинеарные векторы p и q и постройте вектор равный 2p + 1 / 3q (ПЖ срочно)?

Начертите неколлинеарные векторы p и q и постройте вектор равный 2p + 1 / 3q (ПЖ срочно).

Вы находитесь на странице вопроса Даны три неколлинеарных вектора a, b, c Начертите, пожалуйста, как построить : а)А + б — с б) — 2а — б + 3с в) а + 2б — 1 / 2с? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.

70 — 20 = 50 угол BAD 50 — 20 = 30 уголDAC.

🎦 Видео

Разложение вектора по базису. 9 класс.Скачать

№779. Дан вектор р = 3а , где а ≠ 0. Напишите, как направлен каждый из векторов а , -а , ½а, -2аСкачать

Урок 3. Произведение векторов и загадочный угол между векторами. Высшая математика | TutorOnlineСкачать