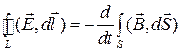Тангенциальная составляющая вектора электрического поля (8 видео)

Граничные условия для тангенциальных составляющих электрического поля

Методика решения данной задачи полностью совпадает с той, которая использовалась при определении граничных условий для тангенциальных составляющих магнитного поля. Отличие состоит в том, что вместо второго уравнения Максвелла (закона полного тока) используется первое уравнение (закон электромагнитной индукции):

В соответствии с этим для малого контура, проведенного по границе раздела двух сред, будем иметь:

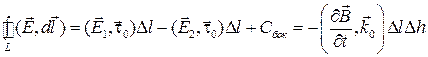
Проводя аналогичные рассуждения, получим

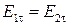
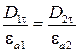
Таким образом, тангенциальные составляющие векторов напряженности электрического поля на границе раздела сред непрерывны, однако аналогичные составляющие векторов электрической индукции, вообще говоря, претерпевают разрыв.

Рассмотрим отдельно граничные условия в том случае, когда средой 2 является идеальный металл. Здесь, как уже известно, 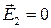. Если бы внутри идеального металла существовала конечная напряженность электрического поля, то это привело бы к протеканию здесь бесконечно больших токов проводимости, и, как следствие, выделению бесконечно большого количества тепла, что противоречит физической сущности задачи. Таким образом, с учетом сказанного, граничное условие для идеального проводника принимает вид

В соответствии с этим условием силовые линии электрического поля должны подходить к поверхности идеального металла по направлению нормали. Понятие «идеальный металл» является абстрактным, и на границе раздела с реальным металлом некоторая тангенциальная составляющая поля все же имеется. Однако, для многих случаев она весьма мала и в реальных задачах ее можно не учитывать.

Дата добавления: 2015-10-19 ; просмотров: 1089 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Содержание

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред
Вектор электрической индукции
Вектор индукции
Связь вектора напряженности и вектора электрического смещения
🔥 Видео

Видео:46. Граничные условия для электрического поляСкачать

Граничные условия для векторов электрического и магнитного поля на границе раздела двух сред

А) Граничные условия для вектора электрической индукции.

Рассмотрим границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе элементарный цилиндр, как показано на рис. 3.1.1.

Тангенциальная составляющая вектора электрического поля

Рис.1.4.1.Элементарный цилиндр, выделенный на границе раздела двух сред для определения граничных условий на вектор электрической индукции. и — нормали к поверхности S.

Согласно теореме Гаусса-Остроградского поток вектора электрической индукции через замкнутую поверхность S равен алгебраической сумме зарядов внутри объема V, ограниченного этой поверхностью:

(3.1.1)

Устремим высоту цилиндра к нулю . Тогда (3.1.1) преобразуется так:

(3.1.2)

Где , – компоненты вектора индукции, перпендикулярные границе раздела, S — площадь основания цилиндра.

Введем поверхностную плотность заряда:

(3.1.3)

Размерность поверхностной плотности заряда = Кл/м2 (Кулон на квадратный метр).

Тогда (3.1.2) можно переписать в виде

(3.1.4)

Если плотность поверхностного заряда равна нулю (), то

. (3.1.5)

Мы можем сформулировать следующее важное утверждение:

На границе раздела, не содержащей поверхностных зарядов, нормальная составляющая вектора электрической индукции непрерывна.

Б) Граничные условия для вектора магнитной индукции.

Рассмотрим границу раздела двух сред, обладающих различной магнитной проницаемостью. Из тех же соображений, что и в предыдущем пункте и принимая во внимание, что магнитных зарядов не существует, можно записать

(3.1.6)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред нормальная составляющая вектора магнитной индукции всегда непрерывна.

В) Граничные условия для вектора напряженности электрического поля .

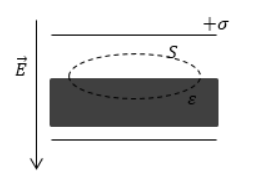
Рассмотрим снова границу раздела двух сред с различными диэлектрическими проницаемостями и . Выделим на границе замкнутый контур в соответствии с рис. 3.1.2. и используем закон электромагнитной индукции:

Где L — выбранный контур, L = 2 (1 + ) , S — площадь поверхности, ограниченная контуром L.

Рис.3.1.2. Контур на границе раздела двух сред, используемый при определении граничных условий для векторов напряженности электрического поля.

Устремим ширину контура к нулю, тогда поток вектора через поверхность S обратится в ноль, и мы получим

(3.1.7)

Откуда следует, что

(3.1.8)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред касательная составляющая вектора напряженности электрического поля всегда непрерывна.

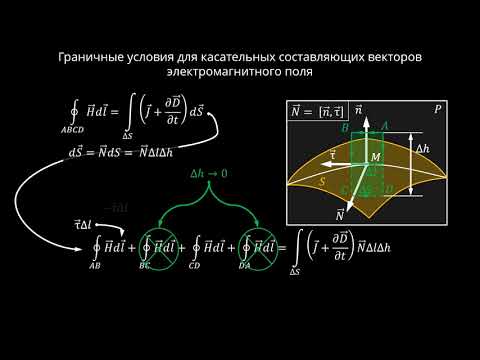
Г) Граничные условия для вектора напряженности магнитного поля Н.

Как в предыдущем случае выделим на границе раздела двух сред замкнутый контур L (рис.1.4.2). Воспользуемся законом полного тока

(3.1.9)

Где — плотность тока, протекающего через поверхность S, ограниченную контуром L.

Учтем, что вдоль границы раздела может течь ток проводимости, тогда при стремлении следует ввести поверхностную плотность тока:

(3.1.10)

Размерность поверхностной плотности тока [] = А/м. Теперь (3.1.9) можно переписать так:

Откуда следует, что

(3.1.11)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред разность касательных составляющих напряженности магнитного поля равна поверхностной плотности тока.

При отсутствии поверхностного тока

(3.1.12)

Это равенство равносильно следующему утверждению:

На границе раздела двух сред, по которой не течет поверхностный ток, касательная составляющая магнитного поля непрерывна.

Д) Граничные условия на поверхности идеального проводника.

Определим идеальный проводник, как проводник, внутрь которого не может проникать электромагнитное поле . Для полей СВЧ-диапазона хорошие проводники (серебро, медь) можно в первом приближении рассматривать как идеальные. На поверхности такого проводника, тем не менее, может течь ток проводимости и формироваться поверхностный заряд. Поэтому на поверхности идеального проводника

, ,

, .

Силовые линии электрического поля перпендикулярны к поверхности идеального проводника; силовые линии магнитного поля касательны к поверхности идеального проводника, как показано на рис.3.1.3.

Рис.3.1.3. Силовые линии электрического и магнитного полей вблизи поверхности идеального проводника.

Видео:44. Электрическое поле в диэлектрике. Вектор поляризованностиСкачать

Вектор электрической индукции

Вектором электрической индукции (электрического смещения) D → называют физическую величину, определяемую по системе С И :

D → = ε 0 E → + P → , где ε 0 — электрическая постоянная, E → — вектор напряженности, P → — вектор поляризации.

Вектор электрического смещения в СНС определяется как:

Видео:Физика - Магнитное полеСкачать

Вектор индукции

Значение вектора D → не является только полевым, потому как он учитывает поляризованность среды. Имеется связь с объемной плотностью заряда, выражаемая соотношением:

По уравнению d i v D → = ρ видно, что для D → единственным источником будут являться свободные заряды, на которых данный вектор начинается и заканчивается. В точках с отсутствующими свободными зарядами вектор электрической индукции является непрерывным. Изменения напряженности поля, вызванные наличием связанных зарядов, учитываются в самом векторе D → .

Видео:Поток вектора напряженности электрического поля. Теорема Гаусса. 10 класс.Скачать

Связь вектора напряженности и вектора электрического смещения

При наличии изотропной среды запись связи вектора напряженности и вектора электрического смещения запишется как:

D → = ε 0 E → + ε 0 χ E → = ε 0 + ε 0 χ E → = ε ε 0 E → .

Где ε – диэлектическая проницаемость среды.

Наличие D → способствует облегчению анализа поля при наличии диэлектрика. Используя теорему Остроградского-Гаусса в интегральном виде с диэлектриком, фиксируется как:

Проходя через границу разделов двух диэлектриков для нормальной составляющей, вектор D → может быть записан:

D 2 n — D 1 n = σ

n 2 → D 2 → — D 1 → = σ ,

где σ – поверхностная плотность распределения зарядов на границе диэлектриков, n 2 → — нормаль, проведенная в сторону второй среды.

Формула тангенциальной составляющей:

D 2 τ = ε 2 ε 1 D 1 τ .

Единица вектора электрической индукции измеряется в системе С И как К л м 2 .

Поле вектора D → изображается при помощи линий электрического смещения.

Определение направления и густоты идет аналогично линиям вектора напряженности. Но линии вектора электрической индукции начинаются и заканчиваются только на свободных зарядах.

Имеются пластины плоского конденсатора с зарядом q . Произойдет ли изменение вектора электрической индукции при заполненном воздухом пространстве между пластинами и диэлектрика с диэлектрической проницаемостью ε ≠ ε υ o z d .

Поле конденсатора в первом случае характеризовалось вектором смещения ε v o z d = 1 , то есть D 1 → = ε v o z d ε 0 E 1 → = ε 0 E 1 → .

Необходимо заполнить пространство между пластинами конденсатора однородным и изотропным диэлектриком. При наличии поля в конденсаторе диэлектрик поляризуется. Тогда начинают появляться связанные заряды с плотностью σ s υ на его поверхности. Создается дополнительное поле с напряженностью:

Векторы полей E → ‘ и E 1 → имеют противоположные направления, причем:

Запись результирующего поля с диэлектриком примет вид:

E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ .

Формула плотности связанных зарядов:

Произведем подстановку σ s υ = χ ε 0 E в E = E 1 — E ‘ = σ ε 0 — σ s υ ε 0 = 1 ε 0 σ — σ s υ , тогда:

Далее выражаем из ( 1 . 6 ) напряженность поля Е . Формула принимает вид:

E = E 1 1 + χ = E 1 ε .

Отсюда следует, что значение вектора электрической индукции в диэлектрике равняется:

D = ε ε 0 E 1 ε = ε 0 E 1 = D 1 .

Ответ: вектор электрической индукции не изменяется.

Была внесена пластина из диэлектрика с диэлектрической проницаемостью ε без свободных зарядов в зазор между разноименными заряженными пластинами. На рисунке 1 показана при помощи штриховой линии замкнутая поверхность. Определить поток электрической индукции Φ D через эту поверхность.

Рисунок 1 . Замкнутая поверхность

Формула записи потока вектора электрического смещения Φ D через замкнутую поверхность S :

Φ D = ∫ S D → · d S → .

Используя теорему Остроградского-Гаусса, можно сказать, что Φ D равняется суммарному свободному заряду, находящемуся внутри заданной поверхности. Из условия видно отсутствие свободных зарядов в диэлектрике и в имеющемся пространстве между пластинами конденсатора, а поток вектора индукции равняется нулю.

Изображена замкнутая поверхность S , проходящая с захватом части пластины изотропного диэлектрика на рисунке 2 . Поток вектора электрической индукции через нее равняется нулю, а поток вектора напряженности > 0 . Какой вывод можно сделать из данной задачи?

Рисунок 2 . Замкнутая поверхность с захватом части пластины изотропного диэлектрика

Из условия имеем, что поток вектора электрического смещения Φ D через замкнутую поверхность равняется нулю, то есть:

Если использовать теорему Остроградского-Гаусса, то значение Φ D – это суммарный свободный заряд, находящийся внутри заданной поверхности. Следует, что внутри такой поверхности отсутствуют свободные заряды:

Φ D = ∫ S D → · d S → = Q = 0 .

Имеем, что поток вектора напряженности не равен нулю, но он считается как сумма свободных и связанных зарядов. Отсюда вывод – диэлектрик содержит связанный заряды.

Ответ: свободные заряды отсутствуют, а связанные есть, причем с положительной их суммой.