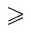Построить четырехугольник по трем сторонам и углам прилежащим к четвертой

Содержание:

Основные задачи на построение циркулем и линейкой:

В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.

При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:

1. с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
2. с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.

Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.

Видео:Построение четырёхугольника по 3 сторонам и 2 углам, прилежащим к 4 сторонеСкачать

Задача 1 (построение угла, равного данному)

От данного луча OF отложите угол, равный данному углу ABC.

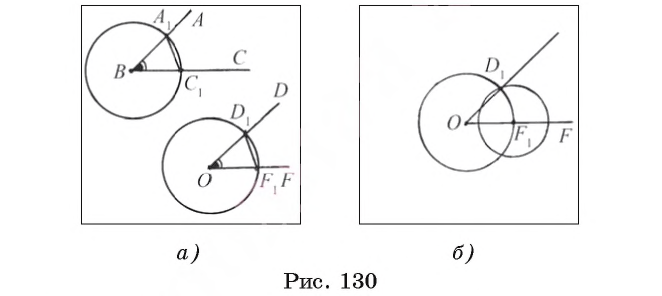
Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).

Пусть

1) Строим окружность (В, R) , где R — произвольный радиус, и отмечаем точки А₁ и С₁ пересечения ее со сторонами угла ABC.

2) Строим окружность 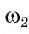(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F₁ с лучом OF.

3) Строим окружность (F₁, A₁C₁).

4) Пусть D₁ — одна из точек пересечения окружностей 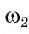(0, R) и (F₁, A₁C₁) (рис. 130, б). Тогда угол D₁OF — искомый. Докажем, что D₁OF =ABC.

Равенство D₁OF =ABC следует из равенства треугольников А₁ВС₁ и D₁OF₁. Действительно, по построению А₁В = D₁O = С₁В = F₁O. Кроме того, по построению F₁D₁ = А₁С₁, следовательно, треугольники А₁ВС₁ и D₁OF₁ равны по трем сторонам. Отсюда следует, что D₁OF =А₁ВС₁, т. е. построенный угол D₁OF равен данному углу ABC.

Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Задача 2 (построение серединного перпендикуляра к отрезку)

Постройте серединный перпендикуляр к данному отрезку АВ.

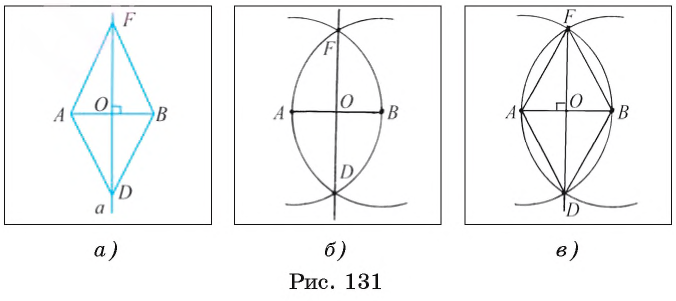
Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности (B, BF) и BF > ОВ. Аналогично AF =AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко увидеть, что AF = BF. Таким образом, точки F и D лежат также и на окружности (A, BF).

1) Строим окружности (A, R) и (B, R) , где R AВ. Пусть, например, R = AB: (A, AB) и (B, AB) (рис. 131, б).

2) Отмечаем точки F и D пересечения окружностей (A, AB) и (B, AB).

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.

Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, AFD = BFD. Отсюда следует, что в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, и высотой и медианой, т. е. прямая FO — серединный перпендикуляр к отрезку АВ.

Видео:Построение треугольника по стороне и двум прилежащим к ней углам. 7 класс. Геометрия.Скачать

Задача 3 (построение биссектрисы угла)

Постройте биссектрису данного угла ABC.

Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.

1) Строим окружность (B, R₁) произвольного радиуса R₁ с центром в вершине В данного угла (рис. 132, б).

2) Отмечаем точки F и D, в которых окружность (B, R) пересекает соответственно стороны ВА и ВС данного угла.

3) Строим окружности (F, R₂) и (D, R₂), где R2 > FD. Отмечаем точку Т их пересечения, которая лежит внутри данного угла.

4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.

Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что FBT = DBT, т. е. луч ВТ — биссектриса угла ABC.

Видео:Построение треугольника по двум сторонам и углу между ними. 7 класс. Геометрия.Скачать

Построение треугольника по трем элементам

В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.

Видео:Построение треугольника по трем сторонам. 7 класс.Скачать

Задача 4 (построение треугольника по двум сторонам и углу между ними)

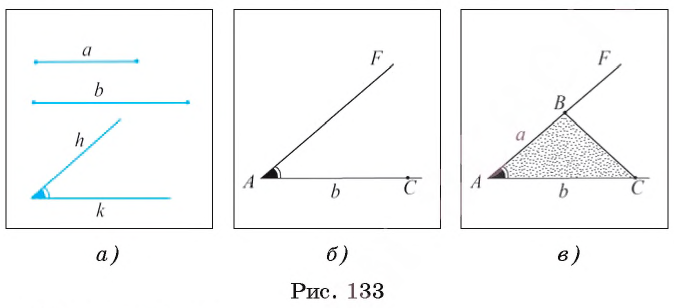
Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.

Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.

1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).

2) Строим угол CAF, равный углу hk.

3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).

По построению имеем, что АС = b, АВ = а и BAC = hk.

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.

Видео:9 класс, 15 урок, Решение треугольниковСкачать

Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)

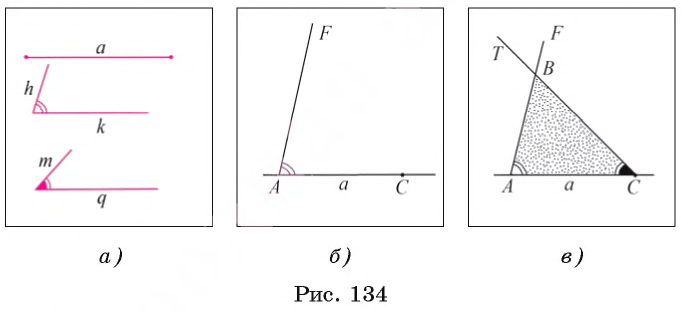
Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.

Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.

1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).

2) Строим угол CAF, равный углу hk.

3) Строим угол ACT, равный углу mq.

4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).

По построению имеем, что АС = a, BAC = hk и ACB = mq.

Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.

Видео:Строим треугольник по стороне и двум углам (Задача 7).Скачать

Задача 6 (построение треугольника по трем сторонам)

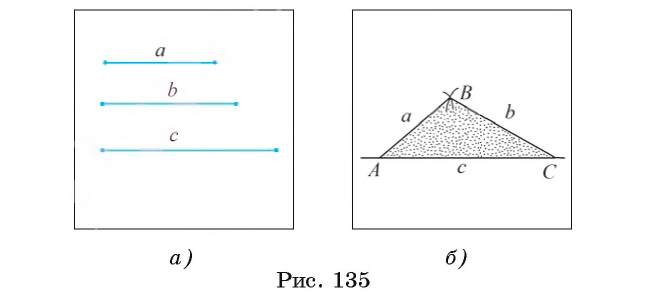
Постройте треугольник, стороны которого равны данным отрезкам а, b, с.

Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.

1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).

2) Строим окружность (A, a).

3) Строим окружность (C, b).

4) Пусть В — одна из точек пересечения окружностей (A, a) и (C, b). Тогда треугольник ABC — искомый.

По построению АС = с, АВ = а, ВС = b.

Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.

• Задачи на построение по геометрии
• Угол — определение, виды, как обозначают с примерами
• Перпендикулярные прямые в геометрии
• Признаки равенства треугольников
• Соотношения между сторонами и углами треугольника
• Неравенство треугольника — определение и вычисление
• Свойства прямоугольного треугольника
• Расстояние между параллельными прямыми

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Строим треугольник по трем сторонам (Задача 5).Скачать

Методы решения задач на построение

Трейдинг криптовалют на полном автомате по криптосигналам. Сигналы из первых рук от мощного торгового робота и команды из реальных профессиональных трейдеров с опытом трейдинга более 7 лет. Удобная система мгновенных уведомлений о новых сигналах в Телеграмм. Сопровождение сделок и индивидуальная помощь каждому. Сигналы просты для понимания как для начинающих, так и для опытных трейдеров. Акция. Посетителям нашего сайта первый месяц абсолютно бесплатно .

Пример 2. Построить четырёхугольник, зная его углы и противоположные

Анализ. Положим, что в четырёхугольнике АВСD стороны BC и AD и углы А, В, С имеют данные значения. Перенесём BC параллельно самой себе в AE, тогда составится треугольник AED, в котором известны две стороны AE и AD и угол EAD, равный разности двух известных углов, данного угла BAD и угла FBC, смежного с данным

CBA. Такой треугольник легко построить. Затем легко провести прямые EC и CD, потому что первая образует известный угол с прямой EA (угол CEG равен углу FBC); а вторая образует известный угол CDA со стороною AD. После этого остаётся только провести CB параллельно EA и решение очевидно.

Строим треугольник АЕD;

Эта задача имеет только одно решение: углы и отношение двух противоположных сторон четырёхугольника вполне определяют его вид.

Основная идея метода подобия состоит в следующем:

Сначала строят фигуру, подобную искомой так, чтобы она удовлетворяла всем условиям задачи, кроме одного. Затем строят уже искомую фигуру, подобную искомой и удовлетворяющую опущенному требованию.

Метод подобия находит применение обычно в случаях, когда среди данных лишь одно является отрезком, а все остальные данные-либо углы, либо отношения отрезков.

Обычно целесообразно вспомогательную фигуру строить так, чтобы она была подобна не только искомой, но и подобно расположена с ней. Успех решения зависит в этих случаях от выбора центра подобия.

При решении задач на построение методом подобия часто воспользоваться следующим замечанием. Если две фигуры подобны, то коэффициент подобия равен отношению любых двух соответствующих отрезков. Если отрезкам a, b, c,… фигуры Ф соответствуют отрезки a1, b1, c1,… подобной фигуры Ф1, то коэффициент подобия равен также отношениям:

Пример 1. Дан Ð АВС и внутри его точка М. Найти на стороне ВС точку Х, расположенную на одинаковом расстоянии от прямой АВ и от точки М.

Анализ. Пусть точка Х найдена так, что перпендикуляр ХY = МХ. Задача сводится к построению фигуры YХМ. Представим целый ряд фигур, подобных искомой фигуре. Достаточно построить одну из этих фигур, например РКN, так как останется провести из точки М прямую параллельную КР и задача будет решена.

Для построения фигуры РКN замечаем, что В есть центр подобия искомых фигур, и поэтому точки М, H, К и В лежат на одной прямой ВМ и PN ^ АВ, PN = BN, положение же точки Р произвольно. Поэтому для построения фигуры PKN надо в произвольной точке Р восстановить PN ^ АВ, из центра N описать радиусом PN дугу, которая пересечёт ВМ в точке К. Проводя МХ ║КN, можно определить искомую точку Х.

Доказательство. Опустив перпендикуляр ХY, из подобия треугольников находим МХ: GH = BX: BN = XY: GE, откуда МХ: GH = =XY: GE, но так как по построению HG = GE, то МХ = YX.

Исследование. Задача всегда возможна и имеет два решения, так как дуга из центра G встречает ВМ всегда в двух точках.

Пример 2. Построить треугольник АВС, если известно отношение АВ: ВС, Ð АВС и радиус вписанной окружности.

Анализ. Так как в искомом треугольнике известен угол и отношение сторон этого угла, то, оставив остальные условия, построим треугольник, подобный искомому. Для этого на сторонах данного угла отложим BD, равную m каких-нибудь равных частей, и ВЕ, равную n таких же частей, и соединим точки D и E. Тогда искомый треугольник и треугольник DBE подобны, так как они имеют по равному углу, заключённому между пропорциональными сторонами. Проводя в угле АВС отрезки, параллельные DE, будем получать треугольники, подобные искомому, но с различными радиусами вписанных окружностей; из всех этих треугольников надо выбрать один, у которого радиус вписанной окружности равен r. Определив центр О, легко построить сам треугольник.

Через G проводим AC ║ DE;

Доказательство. Следует из построения.

Исследование. Возможное решение всегда одно.

Метод геометрического места точек

Геометрическим местом точек называется совокупность точек, обладающих свойствами, исключительно им принадлежащими. Если задача приводится к определению точки, то можно отбросить одно из условий, которому эта точка должна удовлетворять; тогда искомая точка станет способна принять бесчисленное количество последовательных положений, и все эти положения составят геометрическое место точек, обладающих всеми требуемыми свойствами, кроме отброшенного. Фигура этого геометрического места чаще бывает нам заранее известна; в противном случае её надо определить вспомогательными построениями. Затем, приняв отброшенное условие и откинув какое-либо другое условие задачи, мы вновь увидим, что искомая точка станет способна принять бесчисленное множество новых положений, образующих новое геометрическое место. Определим фигуру этого нового геометрического места, если она нам неизвестна. Тогда искомая точка должна лежать и на первом и на втором геометрическом месте, а потому определяется их пересечением.

Иногда для определения точки достаточно построить одно геометрическое место, потому что другое дано в условии задачи. Если же искомая точка подчинена таким условиям, которые все в совокупности определяют только одно геометрическое место, то задача становится неопределённой.

Отсюда видно, как важно знать различные геометрические места. Знание геометрических мест иногда позволяет сразу видеть, где находится неизвестная точка.

Пример 1. Постройте треугольник, если заданы сторона, прилежащий к ней угол и сумма двух других сторон.

Анализ. Пусть ∆АВС уже построен, тогда положение вершин В иС можно считать известным. Остаётся найти вершину А. Выясним свойства точки А. Во-первых, точка А принадлежит лучу (BA), так как дан угол АВС, во-вторых, точка А является вершиной ломанной, состоящей из двух звеньев, сумма которых равна длине данного отрезка, являющегося суммой АВ и АС сторон искомого треугольника.

На продолжении стороны ВА за точку А отложим отрезок АА1, равный отрезку АС. Теперь можно построить треугольник А1ВС по двум сторонам и углу между ними. В равнобедренном (по построению) треугольнике А1АС серединный перпендикуляр к стороне А1С пересечёт луч ВА1 в точке А.

построить ∆ВА1С по сторонам ВС и ВА1 = АВ + АС и углу между ними;

провести серединный перпендикуляр к стороне А1С;

найти точку пересечения луча (BA) и построенного серединного перпендикуляра. Точка пересечения и будет искомой вершиной А.

Доказательство. В построенном ∆АВС сторона ВС, сумма сторон АВ и АС, угол В-данные.

Исследование проведём по ходу построения. Треугольник ВА1С по двум сторонам и углу между ними можно построить единственным образом. Провести серединный перпендикуляр к отрезку А1С – тоже единственным образом. Точка пересечения луча (BA) и серединного перпендикуляра существует и она единственная. Пример 2. Постройте треугольник по стороне, разности углов при при этой стороне и сумме двух других сторон.

Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Геометрические методы решения задач на построение

Видео:Геометрия 10 класс (Урок№2 - Четырехугольники.)Скачать

«Календарь счастливой жизни:
инструменты и механизм работы
для достижения своих целей»

Сертификат и скидка на обучение каждому участнику

Видео:Построение треугольника по углу и двум сторонам. 7 класс.Скачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Описание презентации по отдельным слайдам:

Геометрические методы решения задач на построение

Задача на построение состоит в том, что требуется построить наперед указанными инструментами некоторую фигуру. Каждая фигура, удовлетворяющая условиям задачи, называется решением этой задачи.

Построения более сложных задач сводят к некоторым типичным комбинациям простейших построений, которые называются основными построениями.

Основные построения Отложить на данном луче от его начала отрезок, равный данному отрезку. Отложить от данного луча в данную полуплоскость угол, равный данному углу. Построить треугольник по трем сторонам. Построить треугольник по двум сторонам и углу между ними. Построить треугольник по стороне и двум прилежащим углам. Построить биссектрису данного неразвернутого угла. Построить серединный перпендикуляр данного отрезка Построить середину данного отрезка. Построить прямую, проходящую через данную точку и перпендикулярную данной прямой. Построить прямую, проходящую через данную точку и параллельную данной прямой. Построить прямоугольный треугольник по гипотенузе и острому углу. Построить прямоугольный треугольник по гипотенузе и катету. Построить касательную к окружности, проходящую через данную на ней точку

Схема решения задач на построение Анализ Построение Доказательство Исследование

1. Метод пересечения множеств Сущность метода пересечения состоит в следующем. Задачу сводят к построению одной точки, удовлетворяющей двум условиям α1 и α2 которые вытекают из условий задачи. Пусть F1 – множество точек, удовлетворяющих первому условию, F2 – множество точек, удовлетворяющее второму условию. Тогда искомая фигура находится как пересечение этих множеств точек F1 и F2. Методы решения задач на построение

ТЕОРЕМА. Три отрезка могут быть сторонами треугольника тогда и только тогда, когда один из них меньше суммы и больше разности двух других

Задача. Построить окружность, касательную к двум данным параллельным прямым a и b и проходящую через точку Р. Анализ. Если расстояние между прямыми a и b обозначим d, то радиус окружности равен d/2. Задача сводится к нахождению центра окружности, удовлетворяющего двум условиям: 1) центр равноудален от прямых a и b; 2) центр отстоит от точки Р на расстояние d/2. ● Р d a b

Построение Из произвольной точки А прямой a опускаем перпендикуляр АВ на прямую b Строим серединный перпендикуляр к отрезку АВ Строим множество точек, отстоящих от Р на расстояние d/2, то есть окружность L (P; d/2) с центром в точке Р и радиуса d/2 Строим пересечение L (P; d/2) и с Строим окружность L1 (O; OP), где О принадлежит пересечению L (P; d/2) и с a b ●А ● B ● P c ● ● О

Доказательство Окружность касается прямых, а и b, так как по построению центрокружности находится на одинаковом расстоянии d/2 от прямых, а и b. Кроме того окружность проходит через точку Р. Исследование Возможны три случая расположения точки Р относительно прямых, а и b. 1. Если точка Р лежит между прямыми, а и b, то существуют две окружности, то есть множество L (P; d/2) состоит из двух точек. 2. Если Р принадлежит одной из прямых, а и b, то задача имеет единственное решение. 3. Если точка Р лежит вне полосы, ограниченной прямыми, а и b, то задача не имеет решения. а b • P a b a b • P • P

2. Метод параллельного переноса Сущность метода параллельного переноса заключается в том, что применяя преобразования параллельного переноса, мы приводим данные и искомые элементы фигуры в удобное для построения положение, то есть задача сводится к более простой задаче. В основном метод параллельного переноса применяется при построении многоугольников.

Задача. Построить трапецию по основанию , диагоналям и углу между диагоналями Дано: ●А ●Д ●А ●С ●В ●Д ● О Д А Анализ Допустим что трапеция АВСD построена. Если СК параллельна диагонали ВD, то в треугольнике АСК известны стороны АС, СК и угол между ними. А В С К D

Построение Строим треугольник АСК по сторонам АС,СК и углу АСК На луче АК от точки А откладываем отрезок АD, равный стороне трапеции Строим отрезок DВ параллельно СК Соединяем точку В с точками А и С. Четырехугольник АВСD является искомой трапецией Доказательство По построению, отрезки ВD, АС совпадают с диагоналями трапеции, угол АОD совпадает с данным. Исследование Четырехугольник АВСD строится однозначно, если сторона АD меньше АК Задача решена ● A B● С ● ●D K О

Построить четырехугольник, зная его стороны и угол ϕ, образуемый противоположными сторонами. Дано • A •B • B • C •D • C •A • D Анализ Допустим, что построили искомый четырехугольник АВСD. Если отрезок АО параллелен и равен ВС, то в треугольнике АОD известны две стороны и угол между ними. A B C D O φ φ

Построение Строим треугольник АОD по двум сторонам АО, АD и углу DАО. На стороне ОD строим треугольник ОСD по сторонам ОС и СD. Через точку С проведем прямую параллельно АО Через точку А строим прямую параллельно ОС. Точку пересечения двух построенных прямых обозначим В. Четырехугольник является искомым ● A B● ●D O● ●С Доказательство По построению стороны четырехугольника АВСD равны искомым, угол между прямыми АD и ВС равен углу DAO Исследование Как следует из построения, задача имеет единственное решение. Задача решена

3. Метод симметрии Две точки на плоскости называются симметричными относительно прямой S, они расположены на одном перпендикуляре к прямой S и прямая S делит отрезок АВ пополам. Преобразование, при котором каждой точке данной фигуры ставится в соответствие точка, симметричная ей относительно прямой S, называется осевой симметрией . Метод симметрии заключается в следующем. Предполагают задачу решенной и одной из данных точек отражают в какой-нибудь известной оси. Тогда полученную симметричную точку подчиняют тем же условиям, которым должна быть удовлетворять замененная точка. Причем за ось симметрии выбирается по возможности данная прямая или прямая, которая может быть легко построена. Полученную задачу решают методами и способами ранее известными.

Задача. На данной прямой АВ найти точку Х, соединив которую с данными точками М и N, получим углы NXB и MXA, из которых один вдвое больше другого. А B N M X L C Анализ Пусть точка Х построена так, что 18 слайд

Построение Построим точку С, симметричную М относительно АВ Построим окружность с центром в точке С радиуса СL Из точки N проводим касательную NK к окружности Точка Х пересечение прямой NK с прямой АВ является искомой. B ●N M● ●X L ●C K A Доказательство По построению угол МХL равен углу СХL, а угол КХL в два раза больше угла СХL Исследование Задача всегда имеет решение, если точки М и N не лежат на прямой АВ. Из точки N можно провести две касательные к окружности, поэтому существуют две точки на прямой АВ, удовлетворяющие условию задачи. Аналогичные построения и для точки М. Задача имеет четыре решения.

: Метод вращения вокруг точки Пусть в плоскости даны точки ориентированный угол α. Каждой точке М данной плоскости будем ставить в соответствии такую точку М1, что ОМ=ОМ1 и 20 слайд

Построить квадрат так, чтобы три его вершины лежали на трех данных параллельных прямых a, b и c. Анализ Допустим, что АВСD является искомым квадратом. При вращении плоскости вокруг точки В на 90 градусов, точка С переходит в точку А. Следовательно, точка А должна лежать на прямой с, полученной из С при вращении на 90 градусов. А В С D a b c

Построение Построим образ С прямой с при вращении плоскости вокруг В на 90 градусов. Точку пересечения прямых а и с обозначим А. Радиусом АС с центром в точке В построим окружность γ. Точку пересечения окружности и с обозначим через С С центрами в точках А и С построим окружности γ2 и γ3 радиуса ВС. Тогда, D= γ2 ∩γ3 Доказательство По построению все стороны четырехугольника АВСD равны между собой. Кроме того, угол АВС является прямым. Тогда, очевидно, АВСD является квадратом Исследование Задача всегда имеет решение. Выбирая точку В на различных прямых а, b, c получим три различных решения. Если одна точка из прямых равноудалена от двух других, то полученные квадраты равны. А В D b c a

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 967 человек из 79 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 338 человек из 71 региона

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 691 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

• Рагимов Заур КюроглиевичНаписать 1355 02.03.2020

Номер материала: ДБ-1031815

01.03.2020 17

01.03.2020 25

01.03.2020 47

28.02.2020 22

28.02.2020 17

27.02.2020 92

27.02.2020 33

27.02.2020 24

Не нашли то, что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России

Время чтения: 1 минута

Число участников РДШ за 2021 год выросло в три раза

Время чтения: 2 минуты

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов

Время чтения: 1 минута

Минпросвещения готовит рекомендации по построению «идеальной школы»

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

📺 Видео

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Что такое угол? Виды углов: прямой, острый, тупой, развернутый уголСкачать

Правильные многоугольники. Геометрия 9 класс | Математика | TutorOnlineСкачать

8 класс, 4 урок, ПараллелограммСкачать

Задача, которую боятсяСкачать

7 класс Атанасян. Вся геометрия за 100 минут. Треугольник, окружность, задачи на построениеСкачать

3 правила для вписанного четырехугольника #shortsСкачать

Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать