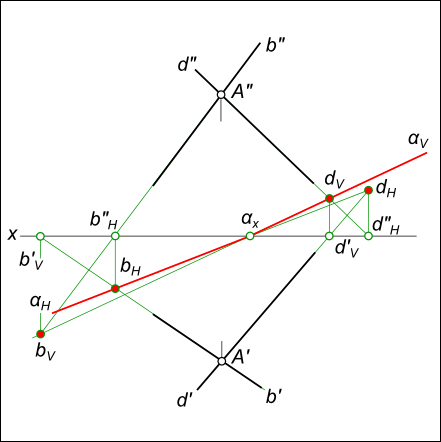
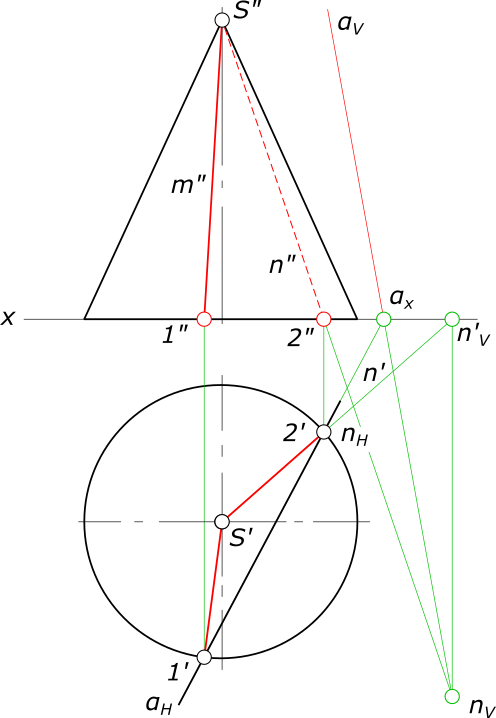
Построение следов плоскости бывает необходимо, когда плоскость задана прямыми, точкой и прямой и тремя точками. Построение следов плоскости производят из условия: если прямая общего положения лежит в плоскости, то ее следы лежат на одноименных следах этой плоскости. Построение следов плоскости α, заданной двумя пересекающимися прямыми
выполняют исходя из того что следы плоскости — это пересекающиеся прямые. Для проведения каждого следа на эпюре необходимы две точки: — для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно; — для фронтального следа αV найдены dV и αx, фронтальный след прямой d и точка схода следов соответственно.
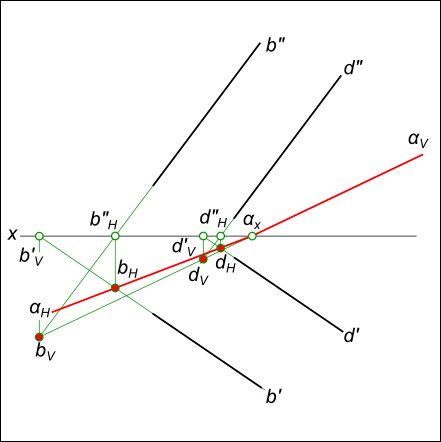
Построение следов плоскости α, заданной двумя параллельными прямыми
Для проведения каждого следа на эпюре необходимы две точки: — для горизонтального следа αH найдены bH и dH, горизонтальные следы прямых b и d соответственно; — для фронтального следа αV найдены bV и αx, фронтальный след прямой d и точка схода следов соответственно.
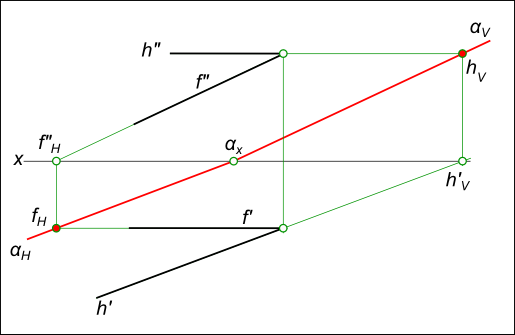
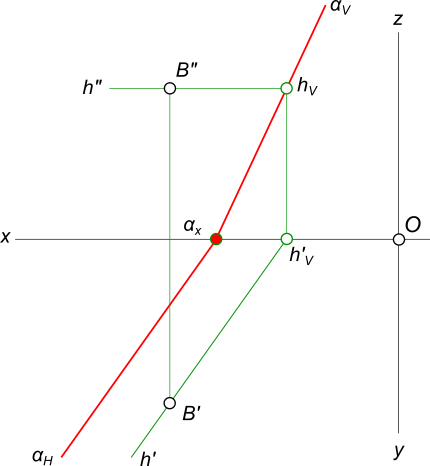
Построение следов плоскости α, заданной пересекающимися горизонталью и фронталью
Для проведения каждого следа на эпюре необходима одна точка: — для горизонтального следа αH найдены fH ; — для фронтального следа αV могут быть использованы hV или αx, фронтальный след прямой h или точка схода следов соответственно.
Если требуется выполнить построение следов плоскости, заданной тремя точками, тогда следует соединить одноименные проекции точек прямыми линиями, которые или пересекаются или параллельны между собой . Дальнейший ход решения показан в выше изложенных примерах.
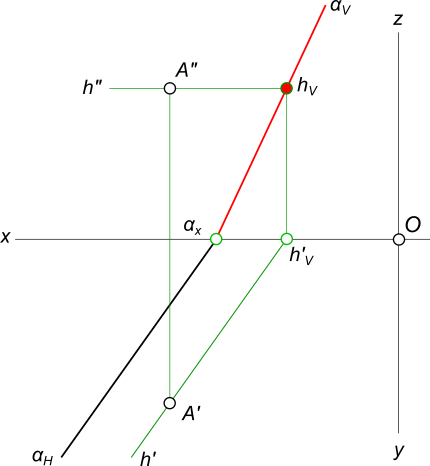
Построение следов плоскости заданной одним из следов и точкой
Через точку A проводим горизонталь h плоскости и находим ее след hV. Проводим фронтальный след плоскости α через след прямой hV и точку схода следов αx.
Построение следов плоскости бывает необходимо, из условия принадлежности точки или прямой плоскости.
Через точку B проводим произвольную прямую h — горизонталь плоскости и находим ее след hV. Проводим фронтальный след αV через след hV произвольного направления. Проводим горизонтальный след αH через точку схода следов αx.
Видео:43. Построение следов плоскости, заданной двумя пересекающимися прямымиСкачать

Следы плоскости
На рисунке показана плоскость общего положения α. Она пересекает плоскости проекций П1, П2, П3 по прямым h0α, f0α и p0α. Эти прямые называются горизонтальным, фронтальным и профильным следом плоскости α.
Оси координат пл. α пересекает в точках Xα, Yα и Zα. Они называются точками схода следов. При этом Xα = h0α ∩ f0α, Yα = h0α ∩ p0α, Zα = f0α ∩ p0α. Здесь знак ∩ означает пересечение.
На комплексном чертеже плоскость можно задать проекциями двух её следов. Это обеспечивает наглядность изображения и удобство при выполнении ряда построений. Стоит отметить, что угол, образованный следами плоскости на комплексном чертеже, не равен углу между ними в пространстве.
Алгоритм построения следов плоскости
На рисунке, который представлен ниже, некоторая плоскость α задана проекциями двух пересекающихся прямых a и b. Чтобы найти её следы, необходимо:
- Построить точки Ha и Hb – горизонтальные следы прямых a и b. Провести через них h0α – горизонтальный след пл. α до пересечения его с осью x.
- Построить точки Fa и Fb – фронтальные следы прямых a и b. Провести через них f0α – одноименный след плоскости α.
- Если построения выполнены верно, то прямые h0α и f0α пересекутся между собой в точке Xα, расположенной на оси проекций.
Решение задачи можно сократить. Для этого, построив горизонтальный след плоскости, фронтальный нужно провести через Xα и одну из точек, Fa или Fb. Таким образом, вместо четырех следов прямых a и b будет достаточно найти три.
Видео:Следы плоскостиСкачать

Задание 1. Построение следов плоскости и определение расстояния от точки до плоскости
Видео:Построение следов плоскостиСкачать

1.1. Условие задания
Построить следы плоскости, заданной ∆BCD, и определить расстояние от точки А до заданной плоскости методом прямоугольного треугольника (координаты точек А, В, С и D см. в Таблице 1 раздела Задания);
Видео:Следы прямойСкачать

1.2. Пример выполнения задания № 1
Первое задание представляет комплекс задач по темам:
1. Ортогональное проецирование, эпюр Монжа, точка, прямая, плоскость: по известным координатам трех точек B, C, D построить горизонтальную и фронтальную проекции плоскости, заданной ∆BCD;
2. Следы прямой, следы плоскости, свойства принадлежности прямой плоскости: построить следы плоскости, заданной ∆BCD;
3. Плоскости общего и частного положения, пересечение прямой и плоскости, перпендикулярность прямой и плоскости, пересечение плоскостей, метод прямоугольного треугольника: определить расстояние от точки А до плоскости ∆BCD.
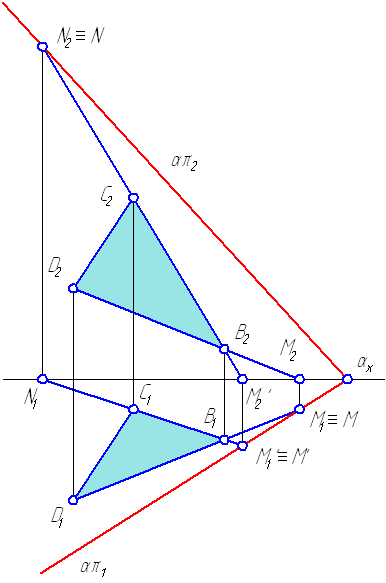
1.2.1. По известным координатам трех точек B, C, D построим горизонтальную и фронтальную проекции плоскости, заданной ∆BCD (Рисунок 1.1), для чего необходимо построить горизонтальные и фронтальные проекции вершин ∆BCD, а затем одноименные проекции вершин соединить.
Известно, что следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с плоскостью проекций.
У плоскости общего положения 3 следа: горизонтальный, фронтальный и профильный.
Для того чтобы построить следы плоскости, достаточно построить следы (горизонтальный и фронтальный) любых двух прямых, лежащих в этой плоскости, и соединить их между собой. Таким образом, след плоскости (горизонтальный или фронтальный) будет однозначно определен, поскольку через две точки на плоскости (в данном случае этими точками будут следы прямых) можно провести прямую, и при том, только одну.
Основанием для такого построения служит свойство принадлежности прямой плоскости: если прямая принадлежит заданной плоскости, то ее следы лежат на одноименных следах этой плоскости.
Следом прямой называется точка пересечения этой прямой с плоскостью проекций.
Горизонтальный след прямой лежит в горизонтальной плоскости проекций, фронтальный – во фронтальной плоскости проекций.
Рассмотрим построение горизонтального следа прямой DB, для чего необходимо:
1. Продолжить фронтальную проекцию прямой DB до пересечения с осью X, точка пересечения М2 является фронтальной проекцией горизонтального следа;
2. Из точки М2 восстановить перпендикуляр (линию проекционной связи) до его пересечения с горизонтальной проекцией прямой DB или ее продолжением. Точка пересечения М1 и будет являться горизонтальной проекцией горизонтального следа (Рисунок 1.1), которая совпадает с самим следом М.
Аналогично выполняется построение горизонтального следа отрезка СВ прямой: точка М’.
Чтобы построить фронтальный след отрезка CB прямой, необходимо:
1. Продолжить горизонтальную проекцию прямой CB до пересечения с осью X, точка пересечения N1 является горизонтальной проекцией фронтального следа;
2. Из точки N1 восстановить перпендикуляр (линию проекционной связи) до его пересечения с фронтальной проекцией прямой CB или ее продолжением. Точка пересечения N2 и будет являться фронтальной проекцией фронтального следа, которая совпадает с самим следом N.
Соединив точки M′1 и M1 отрезком прямой, получим горизонтальный след плоскости απ1. Точка αx пересечения απ1 с осью X называется точкой схода следов. Для построения фронтального следа плоскости απ2 необходимо соединить фронтальный след N2 с точкой схода следов αx
Рисунок 1.1 — Построение следов плоскости
Алгоритм решения этой задачи может быть представлен следующим образом:
1.2.2. Для решения второй части первого задания необходимо знать, что:
- расстояние от точки А до плоскости ∆BCD определяется длиной перпендикуляра, восстановленного из этой точки на плоскость;
- любая прямая перпендикулярна к плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости;
- на эпюре проекции прямой, перпендикулярной плоскости, перпендикулярны наклонным проекциям горизонтали и фронтали этой плоскости или одноименным следам плоскости (рис. 1.2) (см. в лекциях Теорему о перпендикуляре к плоскости).
Чтобы найти основание перпендикуляра, необходимо решить задачу на пересечение прямой (в данной задаче такой прямой является перпендикуляр к плоскости) с плоскостью:
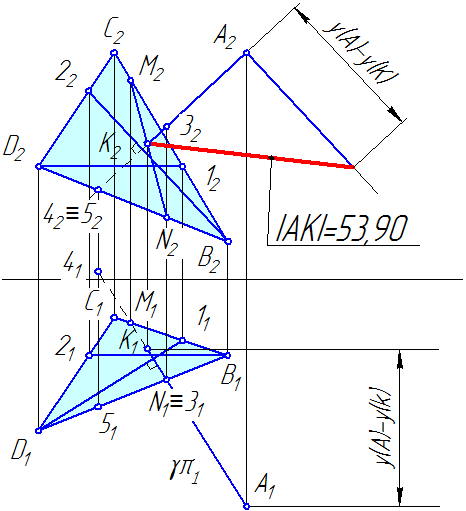
1. Заключить перпендикуляр во вспомогательную плоскость, в качестве которой следует взять плоскость частного положения (горизонтально-проецирующую или фронтально-проецирующую, в примере в качестве вспомогательной плоскости взята горизонтально-проецирующая γ, то есть перпендикулярная к π1, ее горизонтальный след γ1 совпадает с горизонтальной проекцией перпендикуляра);
2. Найти линию пересечения заданной плоскости ∆BCD со вспомогательной γ (MN на рис. 1.2);
3. Найти точку пересечения линии пересечения плоскостей MN с перпендикуляром (точка К на рис. 1.2).
4. Для определения истинной величины расстояния от точки А до заданной плоскости ∆BCD следует воспользоваться методом прямоугольного треугольника: истинная величина отрезка есть гипотенуза прямоугольного треугольника, одним катетом которого является одна из проекций отрезка, а другим – разность расстояний от его концов до плоскости проекций, в которой ведётся построение.
5. Определите видимость участков перпендикуляра методом конкурирующих точек. На примере — точки N и 3 для определения видимости на π1, точки 4, 5 — для определения видимости на π2.
Рисунок 1.2 — Построение перпендикуляра к плоскости 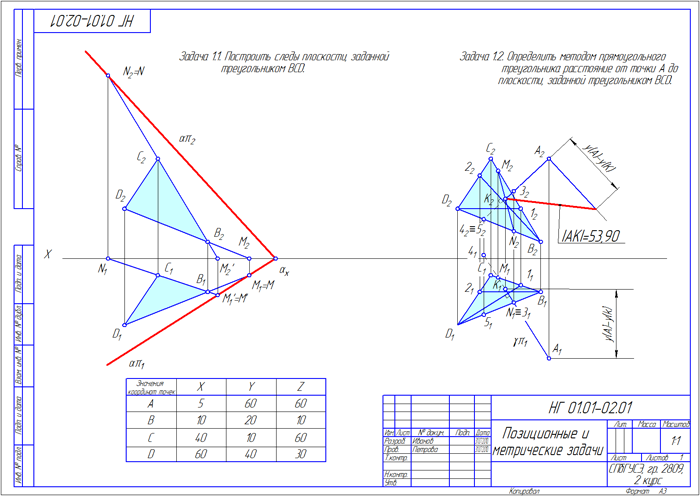
Рисунок 1.3 — Пример оформления контрольного задания №1
🎦 Видео
14. Построение следа плоскости, заданной треугольникомСкачать

Следы плоскости общего положения заданной фронталью и горизонталью. Начертательная геометрия легкоСкачать

Построение следов плоскости заданную пересекающимися прямыми #задачиначертательнаягеометрияСкачать

Следы прямойСкачать

3 Нахождение следов прямойСкачать

Следы прямой Взаимное положение двух прямыхСкачать

Следы плоскостиСкачать

Параллельность прямой к плоскостиСкачать

Построение следов плоскости, заданной треугольникомСкачать

Построение недостающей проекции плоскости. Принадлежность прямой к плоскостиСкачать

Следы плоскости расстоянотточкидоплоскости2653 3Скачать

Построение точки пересечения прямой с плоскостью, заданной следамиСкачать
Построение недостающих проекций, следы плоской фигурыСкачать
Построение параллельной плоскости на расстояние 30 мм.Скачать

Лекция 4. ПлоскостьСкачать

Определение кратчайшего расстояние между скрещивающимися прямыми методом замены плоскостей проекцииСкачать