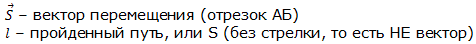Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.
Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.
Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.
Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.
Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.
Видео:Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать
Вектор перемещения
Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.
Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.
Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).
Рис. 1.1. Вектор перемещения и пройденный путь.
Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.
Правило сложения векторов
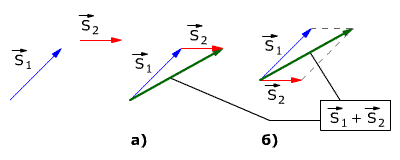
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).
Рис. 1.2. Сложение векторов перемещений.
На рис 1.2 показаны правила сложения векторов S1 и S2:
а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма
Видео:Понятие вектора. Коллинеарные вектора. 9 класс.Скачать
Проекции вектора перемещения
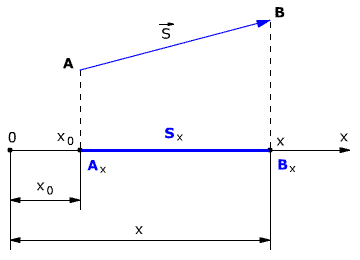
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения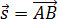 
(рис. 1.3).
Выберем ось ОХ так, чтобы вектор 
лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно Аx и Вx. Длина отрезка АxВx на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть
Рис. 1.3. Проекция вектора перемещения.
Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:
Здесь x0, y0, z0 — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).
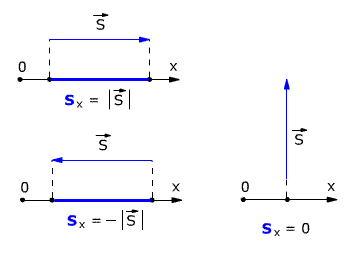
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).
Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).
Рис. 1.4. Модули проекции вектора перемещения.
Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.
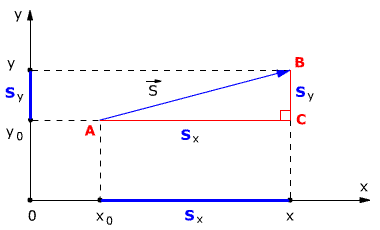
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х0 и у0, то есть А(х0, у0). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.
Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).
Рис. 1.5. Движение тела на плоскости.
Определим проекции вектора перемещения на осях ОХ и OY:
На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как
По теореме Пифагора
Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:
Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.
Видео:Зачем нужен ВЕКТОР. Объяснение смыслаСкачать
Введение в тригонометрию
план-конспект занятия по алгебре (10 класс) по теме
Выступление на заседании районного МО учителей математики.
Видео:Разложение вектора по базису. 9 класс.Скачать
Скачать:
| Вложение | Размер |
|---|---|
| eysert_svetlana_nikolaevna.docx | 262.38 КБ |
Видео:✓ Что такое вектор? Чем отличается понятие "вектор" от понятия "направленный отрезок" | Борис ТрушинСкачать
Предварительный просмотр:
Тема: ВВЕДЕНИЕ В ТРИГОНОМЕТРИЮ
Эйсерт Светлана Николаевна
Муниципальное бюджетное образовательное учреждение средняя общеобразовательная школа № 2
ПОНЯТИЕ УГЛА. Вв едем на плоскости прямоугольную систему координат хОу и рассмотрим окружность радиуса R=1 с центром в начале координат. Обозначим точки пересечения окружности с осями координат: А(1; 0), В(0; 1), С(-1; 0), Д(0; -1).
Пусть на окружности дана точка М. Вектор, начало которого – точка О, а конец точка М, движущаяся по окружности. Этот вектор назовем подвижным вектором . Угол АОМ получен поворотом подвижного вектора до вектора . В тригонометрии принято считать, что любой поворот подвижного вектора образует угол. Если подвижный вектор совершил такой поворот, что впервые его конечное положение совпало с начальным положением (вектор ), то такой поворот называют полным поворотом. В тригонометрии принято считать углы, образованные поворотом подвижного вектора против часовой стрелки, положительными , а углы, образованные поворотом подвижного вектора по часовой стрелке отрицательными . Если подвижный вектор не совершил поворота, то считаем, что образован нулевой угол . Если подвижный вектор совершил поворот, равный 1360 части полного поворота против часовой стрелки, то говорят, что образован угол, градусная мера которого равна одному градусу или угол в один градус . Совершив полный оборот против часовой стрелки, получим угол в 360° , а совершив один полный оборот по часовой стрелке, получим угол в -360 °. Строя углы в половину полного оборота, в четверть полного оборота против часовой, или по часовой стрелке, получаем углы 180°, -180°, 90°, -90° . Напомним, что одна минута равна 160 градуса, а одна секунда равна 160 минуты.
От начального вектора можно отложить любой угол градусной меры α , где α – любое действительное число, в положительном направлении при α больше нуля и в отрицательном направлении при а меньше нуля. Градусную меру такого угла можно записать в виде: α = + 360k, где k- некоторое целое число, — угол от 0 ° до 360 °.
РАДИАННАЯ МЕРА УГЛА
Если подвижный вектор совершил поворот против часовой стрелки так, что его конец прошел расстояние равное радиусу окружности, то говорят, что образован угол в один радиан, радианная мера которого равна одному радиану. Радиан -это величина центрального угла окружности радиуса R , опирающегося на дугу длины R. это определение не зависит от R , поэтому обычно выбирают R = 1. Длина окружности равна 2πR, поэтому совершив один полный оборот против часовой стрелки, получим угол в 2π радиан, равный 360°. Угол 180 ° равен π радианам. Аналогично градусную меру любого угла можно перевести в радианную. Градусную меру любого угла можно записать в виде:
α = +2Пk, где k – некоторое целое число.
ОПРЕДЕЛЕНИЕ СИНУСА И КОСИНУСА УГЛА
Число, равное ординате точки единичной окружности, соответствующей углу, называют синусом угла α и обозначают sinα . Число, равное абсциссе точки единичной окружности, соответствующей углу, называют косинусом угла α и обозначают cosα .
х = cosα, у =sin α . Любая точка единичной окружности имеет координаты М(cosα;sin α )Для любого угла существует единственное значение синуса и косинуса.
Отрезок АВ назовем линией косинусов , отрезок СД назовем линией синусов .
В первой и в четвертой координатных четвертях абсциссы точек положительны, во второй и третьей четвертях – отрицательны поэтому значения косинусов для углов от 0° до 90 ° и для углов от 180° до 270° – положительны, а для углов от 90°до 180° и для углов от 270° до 360° — отрицательны. В первой и во второй координатных четвертях ординаты точек положительны, в третьей и четвертой четвертях – отрицательны, поэтому значения синусов для углов от 0° до 180° — положительные, а для углов от 180° до 360° – отрицательные. В силу периодичности тригонометрических функций, можно определить знаки синусов, косинусов, тангенсов и котангенсов для любых углов.
Координаты точек: А; В; С; Д помогут определить значения синусов и косинусов для углов 0°; 90°; 180°; 360°: А(1; 0), cos0° = 1, sin0° = 0; В(0; 1), cos90° = 0, sin90° = 1; С(-1;0), cos180° = -1, sin180° = 0; Д(0; -1), cos360° = 0, sin360° = -1 .
Так как тангенс есть отношение синуса угла к косинусу, котангенс есть отношение косинуса к синусу, то tg 0° = 0, tg90° — не существует, tg180° = 0, tg360° – не существует, ctg0° – не существует, ctg90° = 0, ctg180° – не существует, ctg360° = 0
ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ НЕКОТОРЫХ УГЛОВ
Построим в системе координат углы: π6, 2π6 = π3, 3π6 = π2, 4π6 = 2π3, 5π6, 6π6 = π, 7π6, 8π6, = 4π3, 9π6 = 3π2, 10π6 = 5π3, 11π6, 12π6 = 2π; π4, 2π4 = π2, 3π4, 4π4, 5π4, 6π4 = 3π2, 7π4, 8π4 = 2π;
Опустим перпендикуляры из точек пересечения единичной окружности со сторонами углов ( , , ,….) на ось Ох. Получим по три точки справа и слева от нуля. Используя теорему Пифагора, получим значения абсцисс 12; 2; ; -12; — 2; — 2. Это и есть значения косинусов для построенных углов. Построив перпендикуляры из точек на окружности к оси Оу, получим значения синусов построенных углов: 12; 2; ; -12; — 2; — 2.
Через точку А (1; 0) проведем прямую параллельную оси Оу, назовем ее линией тангенсов. Проведем лучи , … Точки пересечения с линией тангенсов и есть значения тангенсов построенных углов. Используя теорему Пифагора, получим числа 1 ; 1; ; -1 ; -1; — . Через точку В(0; 1) проведем прямую параллельную оси Ох. Назовем ее линией котангенсов. Точки пересечения лучей , ….с линией котангенсов есть значения котангенсов построенных углов: 1 ; 1; ; -1 ; -1; — .
Совместим все картинки на одном рисунке, которым удобно пользоваться при решении тригонометрических уравнений и неравенств.
Видео:Что такое векторный базис? Душкин объяснитСкачать
Траектория, длина пути, вектор перемещения
Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.
Видео:Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать
Виды движений тела
Существуют несколько видов движений и траекторий твердого тела:
- поступательное;
- вращательное, то есть движение по окружности;
- плоское, то есть перемещение по плоскости;
- сферическое, характеризующее движение по поверхности сферы;
- свободное, иначе говоря, произвольное.
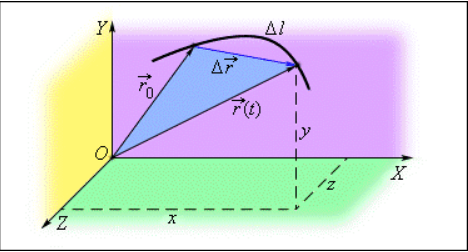
Рисунок 1 . Определение точки при помощи координат x = x ( t ) , y = y ( t ) , z = z ( t ) и радиус-вектора r → ( t ) , r 0 → является радиус-вектором точки в начальный момент времени
Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x = x ( t ) , y = y ( t ) , z = z ( t ) или от времени радиус-вектора r → = r → ( t ) , проведенного из начала координат к заданной точке. Это показано на рисунке 1 .
Видео:Геометрия - 9 класс (Урок№1 - Понятие вектора. Равенство векторов)Скачать
Перемещение тела
Перемещение тела s → = ∆ r 12 → = r 2 → — r 1 → – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t .
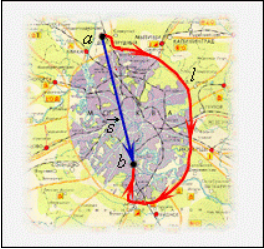
Рисунок 2 . Пройденный путь l и вектор перемещения s → при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике
По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.
Перемещение принято считать векторной величиной. Этот отрезок имеет направление.
Путь – скалярная величина. Считается числом.
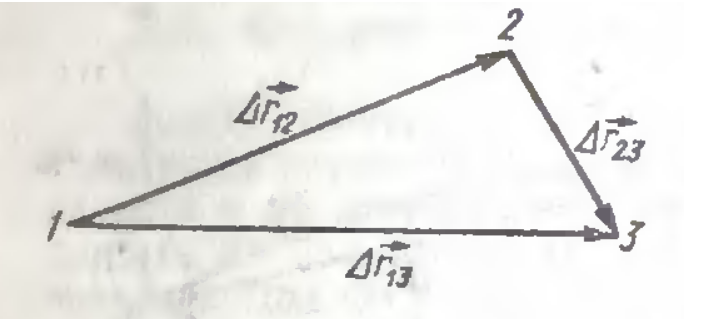
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3 , как показано на рисунке 3 .
Рисунок 3 . Сумма двух последовательных перемещений ∆ r → 13 = ∆ r → 12 + ∆ r → 23 = r → 2 — r → 1 + r → 3 — r → 2 = r → 3 — r → 1
Когда радиус-вектор материальной точки в определенный момент времени t является r → ( t ) , в момент t + ∆ t есть r → ( t + ∆ t ) , тогда ее перемещение ∆ r → за время ∆ t равняется ∆ r → = r → ( t + ∆ t ) — r → ( t ) .
Перемещение ∆ r → считается функцией времени t : ∆ r → = ∆ r → ( t ) .
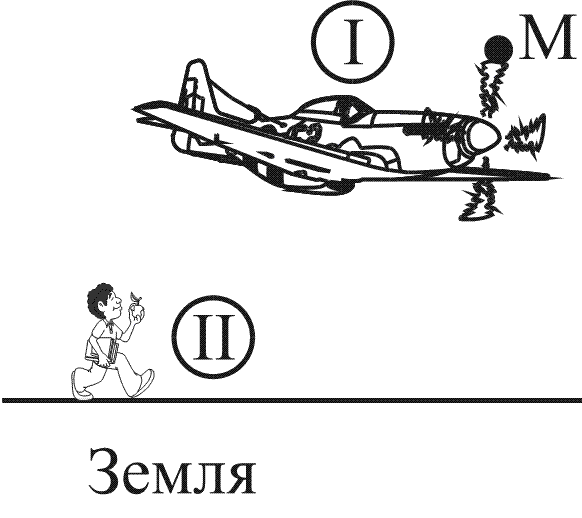
По условию дан движущийся самолет, представленный на рисунке 4 . Определить вид траектории точки М .
Необходимо рассмотреть систему отсчета I , называемую «Самолет» с траекторией движения точки М виде окружности.
Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.
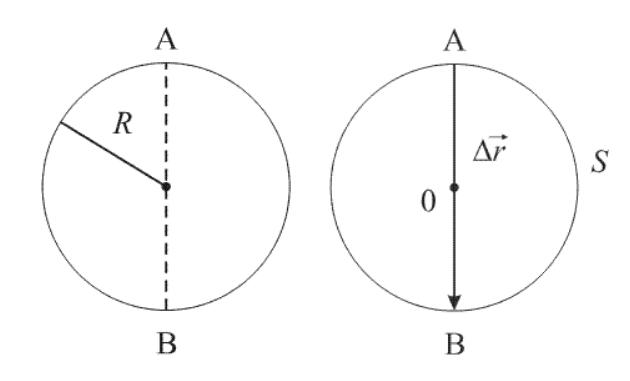
Дана материальная точка, которая совершает движение из А в В . Значение радиуса окружности R = 1 м . Произвести нахождение S , ∆ r → .
Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:
Подставляем числовые значения и получаем:
S = 3 , 14 · 1 м = 3 , 14 м .
Перемещением ∆ r → в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В .
📸 Видео
Как разложить вектор по базису - bezbotvyСкачать
Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать
Построение проекции вектора на осьСкачать
8 класс, 40 урок, Понятие вектораСкачать
Радиус векторСкачать
ПОЧЕМУ KRISS VECTOR НЕ ИМЕЕТ ОТДАЧИСкачать
СКАЛЯРНОЕ УМНОЖЕНИЕ ВЕКТОРОВ ЧАСТЬ I #математика #егэ #огэ #формулы #профильныйегэ #векторыСкачать
ВЫЧИТАНИЕ ВЕКТОРОВ ЧАСТЬ I #егэ #огэ #математика #геометрия #профильныйегэСкачать
Векторы и действия над ними, проекция вектора на координатные оси. 9 класс.Скачать
Коллинеарные векторы.Скачать
Физика | Ликбез по векторамСкачать
ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)Скачать
