Определение 1. Система векторов 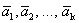
Определение 1´. Система векторов 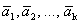
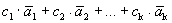
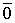
Покажем, что эти определения эквивалентны.
Пусть выполняется определение 1, т.е. один из векторов системы равен линейной комбинации остальных:
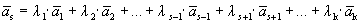
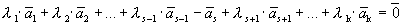
Линейная комбинация системы векторов равна нулевому вектору, причем не все коэффициенты этой комбинации равны нулю, т.е. выполняется определение 1´.
Пусть выполняется определение 1´. Линейная комбинация системы векторов равна 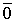
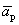
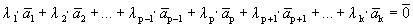
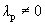
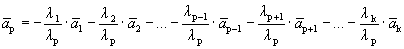
Один из векторов системы мы представили в виде линейной комбинации остальных, т.е. выполняется определение 1.
Определение 2. Единичным вектором, или ортом, 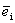
. 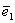
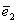
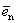
Теорема 1. Различные единичные векторы n -мерного пространства линейно независимы.
Доказательство. Пусть линейная комбинация этих векторов с произвольными коэффициентами равна нулевому вектору.
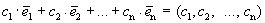
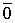
Из этого равенства следует, что все коэффициенты равны нулю. Получили противоречие.
Каждый вектор n -мерного пространства ā(а 1 , а 2 , . а n ) может быть представлен в виде линейной комбинации единичных векторов с коэффициентами, равными координатам вектора
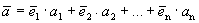
Теорема 2. Если системы векторов содержит нулевой вектор, то она линейно зависима.
Доказательство. Пусть дана система векторов 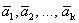
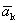
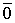
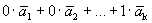
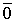
Следовательно, система линейно зависима.
Теорема 3. Если некоторая подсистема системы векторов линейно зависима, то и вся система линейно зависима.
Доказательство. Дана система векторов 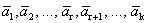
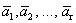
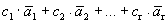
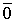
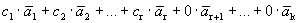
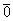
Получилось, что линейная комбинация векторов всей системы равна 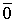
Следствие. Если система векторов линейно независима, то и любая ее подсистема также линейно независима.
Предположим противное, т.е. некоторая подсистема линейно зависима. Из теоремы следует, что вся система линейно зависима. Мы пришли к противоречию.
Теорема 4 (теорема Штейница). Если каждый из векторов 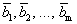
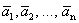
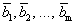
Следствие. В любой системе n -мерных векторов не может быть больше чем n линейно независимых.
Доказательство. Каждый n -мерный вектор выражается в виде линейной комбинации n единичных векторов. Поэтому, если система содержит m векторов и m > n , то, по теореме, данная система линейно зависима.
Видео:Линейная зависимость векторовСкачать

14. Линейная зависимость и независимость векторов
Пусть L – линейное пространство над полем Р. Пусть А1, а2, … , аn (*) конечная система векторов из L. Вектор В = a1×А1 + a2×А2 + … + an×Аn ( 16) называется Линейной комбинацией векторов (*), или говорят, что вектор В линейно выражается через систему векторов (*).
Определение 14. Система векторов (*) называется Линейно зависимой, тогда и только тогда, когда существует такой ненулевой набор коэффициентов a1, a2, … , an, что a1×А1 + a2×А2 + … + an×Аn = 0. Если же a1×А1 + a2×А2 + … + an×Аn = 0 Û a1 = a2 = … = an = 0, то система (*) называется Линейно независимой.
Свойства линейной зависимости и независимости.
10. Если система векторов содержит нулевой вектор, то она линейно зависима.
Действительно, если в системе (*) вектор А1 = 0, То 1×0 + 0×А2 + … + 0×Аn = 0.
20. Если система векторов содержит два пропорциональных вектора, то она линейно зависима.
30. Конечная система векторов (*) при n ³ 2 линейно зависима тогда и только тогда, когда хотя бы один из её векторов является линейной комбинацией остальных векторов этой системы.
Þ Пусть (*) линейно зависима. Тогда найдётся ненулевой набор коэффициентов a1, a2, … , an, при котором a1×А1 + a2×А2 + … + an×Аn = 0 . Не нарушая общности, можно считать, что a1 ¹ 0. Тогда существует 


Ü Пусть один из векторов (*) является линейной комбинацией остальных. Можно считать, что это первый вектор, т. е. А1 = B2А2 + … + bnАN, Отсюда (–1)×А1 + b2А2 + … + bnАN = 0, т. е. (*) линейно зависима.
Замечание. Используя последнее свойство, можно дать определение линейной зависимости и независимости бесконечной системы векторов.
Определение 15. Система векторов А1, а2, … , аn , … (**) называется Линейно зависимой, Если хотя бы один её вектор является линейной комбинацией некоторого конечного числа остальных векторов. В противном случае система (**) называется Линейно независимой.
40. Конечная система векторов линейно независима тогда и только тогда, когда ни один из её векторов нельзя линейно выразить через остальные её векторы.
50. Если система векторов линейно независима, то любая её подсистема тоже линейно независима.
60. Если некоторая подсистема данной системы векторов линейно зависима, то и вся система тоже линейно зависима.
Пусть даны две системы векторов А1, а2, … , аn , … (16) и В1, в2, … , вs, … (17). Если каждый вектор системы (16) можно представить в виде линейной комбинации конечного числа векторов системы (17), то говорят, что система (17) линейно выражается через систему (16).
Определение 16. Две системы векторов называются Эквивалентными, если каждая из них линейно выражается через другую.
Теорема 9 (основная теорема о линейной зависимости).
Пусть 

Доказательство. Предположим, что N > S. По условию теоремы

Так как система 





совместна. Так как число уравнений больше числа неизвестных, то система имеет бесконечно много решений. Следовательно, у неё есть ненулевое решение Х10, х20, …, хN0. При этих значениях равенство (18) будет верно, что противоречит тому, что система векторов 
Следствие. Если две эквивалентные системы векторов конечны и линейно независимы, то они содержат одинаковое число векторов.
Определение 17. Система векторов называется Максимальной линейно независимой системой векторов Линейного пространства L, если она линейно независима, но при добавлении к ней любого вектора из L , не входящего в эту систему, она становится уже линейно зависимой.
Теорема 10. Любые две конечные максимальные линейно независимые системы векторов из L Содержат одинаковое число векторов.
Доказательство следует из того, что любые две максимальные линейно независимые системы векторов эквивалентны.
Легко доказать, что любую линейно независимую систему векторов пространства L можно дополнить до максимальной линейно независимой системы векторов этого пространства.
1. Во множестве всех коллинеарных геометрических векторов любая система, состоящая их одного ненулевого вектора, является максимальной линейно независимой.
2. Во множестве всех компланарных геометрических векторов любые два неколлинеарных вектора составляют максимальную линейно независимую систему.
3. Во множестве всех возможных геометрических векторов трёхмерного евклидова пространства любая система трёх некомпланарных векторов является максимальной линейно независимой.
4. Во множестве всех многочленов степени не выше N С действительными (комплексными) коэффициентами система многочленов 1, х, х2, … , хn Является максимальной линейно независимой.
5. Во множестве всех многочленов с действительными (комплексными) коэффициентами примерами максимальной линейно независимой системы являются
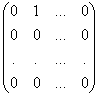
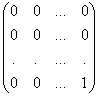
6. Множество матриц размерности M´N является линейным пространством (проверьте это). Примером максимальной линейно независимой системы в этом пространстве является система матриц Е11 = 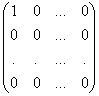
Пусть дана система векторов С1, с2, … , ср (*). Подсистема векторов из (*) называется Максимальной линейно независимой Подсистемой Системы (*), если она линейно независима, но при добавлении к ней любого другого вектора этой система она становится линейно зависимой. Если система (*) конечна, то любая её максимальная линейно независимая подсистема содержит одно и то же число векторов. (Доказательство проведите самостоятельно). Число векторов в максимальной линейно независимой подсистеме системы (*) называется Рангом Этой системы. Очевидно, эквивалентные системы векторов имеют одинаковые ранги.
Видео:Линейно-независимая подсистема системы векторовСкачать

Линейная зависимость и независимость векторов
Набор векторов называется системой векторов .
Система из векторов называется линейно зависимой , если существуют такие числа , не все равные нулю одновременно, что
Система из векторов называется линейно независимой, если равенство (1.1) возможно только при , т.е. когда линейная комбинация в левой части равенства (1.1) тривиальная.
1. Один вектор тоже образует систему: при — линейно зависимую, а при — линейно независимую.
2. Любая часть системы векторов называется подсистемой .
Видео:Линейные комбинации, span и базисные вектора | Сущность Линейной Алгебры, глава 2Скачать

Свойства линейно зависимых и линейно независимых векторов
1. Если в систему векторов входит нулевой вектор, то она линейно зависима
2. Если в системе векторов имеется два равных вектора, то она линейно зависима.
3. Если в системе векторов имеется два пропорциональных вектора , то она линейно зависима.
4. Система из 1″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAC8AAAAQCAMAAACx1dbmAAAAM1BMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAADbQS4qAAAAEHRSTlMAiXFYMbEhAcBBoPDQoeAQ0I3cqgAAALZJREFUKM+VktsSwyAIRDWKiFf+/2uLSZvEhkxaXnTGs7KsGvN3UYrwC+ffa3D8zCMlxo+QlyfcNmg7v7A/t7VBux/jzkOe54lJURw8ZrHvop0UdM8P+3axGc89aqQ7XuxbjzybMkEUqPLAIPP6/u0g1OYUHnMpTQs02KLxq/0p0Y1O0al+RvqOCcv51CeZF1UeJBjhacoT6PJehTd9k/R7gdgPul7ei3itcWeYPp/sqv4fRhnzAuOaBpbDogV3AAAAAElFTkSuQmCC» /> векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов есть линейная комбинация остальных.
5. Любые векторы, входящие в линейно независимую систему, образуют линейно независимую подсистему.
6. Система векторов, содержащая линейно зависимую подсистему, линейно зависима.
7. Если система векторов линейно независима, а после присоединения к ней вектора оказывается линейно зависимой, то вектор можно разложить по векторам , и притом единственным образом, т.е. коэффициенты разложения находятся однозначно.
Докажем, например, последнее свойство. Так как система векторов — линейно зависима, то существуют числа , не все равные 0, что . В этом равенстве . В самом деле, если , то . Значит, нетривиальная линейная комбинация векторов равна нулевому вектору, что противоречит линейной независимости системы . Следовательно, и тогда , т.е. вектор есть линейная комбинация векторов . Осталось показать единственность такого представления. Предположим противное. Пусть имеется два разложения и , причем не все коэффициенты разложений соответственно равны между собой (например, ).
Тогда из равенства получаем .
Следовательно, линейная комбинация векторов равна нулевому вектору. Так как не все ее коэффициенты равны нулю (по крайней мере ), то эта комбинация нетривиальная, что противоречит условию линейной независимости векторов . Полученное противоречие подтверждает единственность разложения.
Пример 1.3. Параллелограмм построен на векторах и ; точки и — середины сторон и соответственно (рис. 1.11). Требуется:
а) найти линейные комбинации векторов
б) доказать, что векторы , , линейно зависимы.
а) Так как , то по правилу треугольника: .
Рассуждая аналогично, получаем: . Построим вектор . Из равенства треугольников и следует, что . Тогда .
б) Учитывая, что и , получаем: .
Перенося векторы в левую часть, приходим к равенству , т.е. нетривиальная линейная комбинация векторов , , равна нулевому вектору. Следовательно, векторы , , линейно зависимы, что и требовалось доказать.
🎬 Видео
Линейная зависимость и линейная независимость векторов.Скачать

Образуют ли данные векторы базисСкачать

Что такое вектора? | Сущность Линейной Алгебры, глава 1Скачать

Высшая математика. Линейные пространства. Векторы. БазисСкачать

Линейная зависимость и линейная независимость. ТемаСкачать

Лекция 16. Понятие вектора и векторного пространства. Базис векторного пространства.Скачать

Линейная зависимость векторов на примерахСкачать

Линейная комбинация. Линейная зависимость (независимость) матриц.Скачать

Что такое векторный базис? Душкин объяснитСкачать

Примеры Линейная зависимость векторов Базис и ранг системы векторовСкачать

Как разложить вектор по базису - bezbotvyСкачать

Что такое вектор системно. ВектораВсем. Проект Вячеслава ЮневаСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Примеры линейной зависимости векторов.Скачать
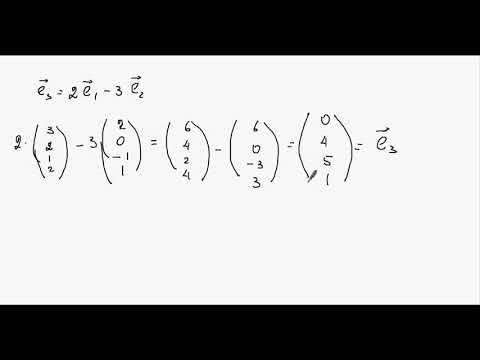
Базис. Разложение вектора по базису.Скачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

Линейная зависимость и независимость систем векторовСкачать

