Как найти координаты вектора xyz

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора

<table data-id="254" data-view-id="254_31110" data-title="Координаты вектора" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value=" AB = <B_x — A_x; B_y — A_y> » data-order=» AB = <B_x — A_x; B_y — A_y> » style=»min-width:55.0847%; width:55.0847%;»> AB = <B_x — A_x; B_y — A_y>Для трехмерных задач

<td data-cell-id="B2" data-x="1" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" AB = <B_x — A_x; B_y — A_y; B_z — A_z> » data-order=» AB = <B_x — A_x; B_y — A_y; B_z — A_z> «> AB = <B_x — A_x; B_y — A_y; B_z — A_z>Для n-мерных векторов

<td data-cell-id="B3" data-x="1" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n> » data-order=» AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n> «> AB = <B₁ — A₁; B₂ — A₂; . B_n — A_n>

Примеры задач

Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .

Задание 2
Определим координаты точки B вектора , если координаты точки .

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB _x + A_x = 6 + 2 = 8.
B_y = AB _y + A_y = 14 + 5 = 19.

Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

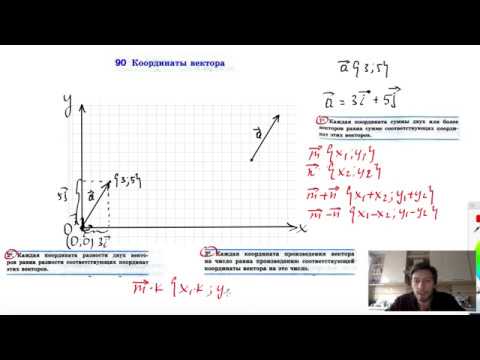
Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Как найти координаты вектора

Формула

Чтобы найти координаты вектора $overline $, если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае если точки заданы на плоскости и имеют соответственно координаты $Aleft(x_ ; y_right)$ и $Bleft(x_ ; y_right)$, то координаты вектора $overline $ вычисляются по формуле:

Примеры нахождения координат вектора

Задание. Даны точки $A(5 ; 1)$ и $B(4 ;-3)$. Найти координаты векторов $overline $ и $overline $

Решение. Точки заданны на плоскости, поэтому координаты вектора $overline $ вычислим по формуле:

Подставляя координаты заданных точек, получим:

Для нахождения вектора $overline $ исходная формула примет вид:

Ответ. $overline=(-1 ;-4), overline=(1 ; 4)$

Задание. Даны точки $A(4 ; 3 ; 2)$, $B(-3 ; 2 ;-1)$ и $C(-1 ; 0 ; 1)$ . Найти координаты вектора $overline $, $overline $ .

Решение. Точки заданны в пространстве, поэтому для нахождения координат искомых векторов будем пользоваться формулой

Подставляя заданные координаты, получим:

Для вектора $overline $ имеем:

Ответ. $overline=(-7 ;-1 ;-3), overline=(-2 ; 2 ;-2)$

🎥 Видео