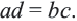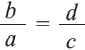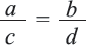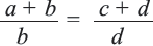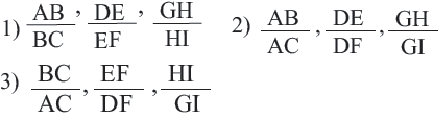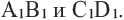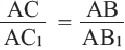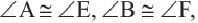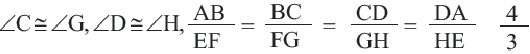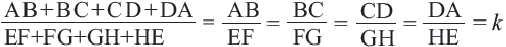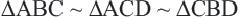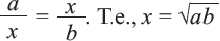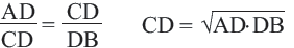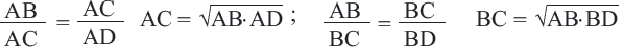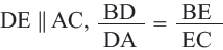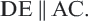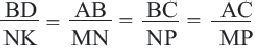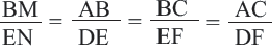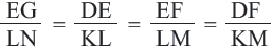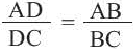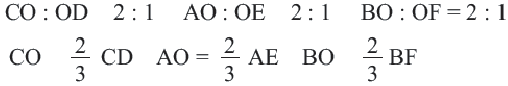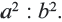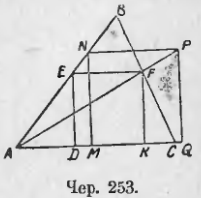Содержание:
Отображение плоскости на себя, которое сохраняет расстояния между точками, называется движением. Примерами движения являются такие преобразования, как центральная симметрия, осевая симметрия, поворот (вращение), скольжение.
Поворот:
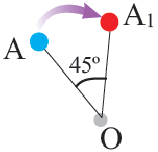
Пусть, заданы точка О и угол
1. Если точка А не совпадает с точкой О, то
2. Если точка А совпадает с точкой О, то точки 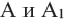
Пример 1. Угол поворота 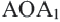
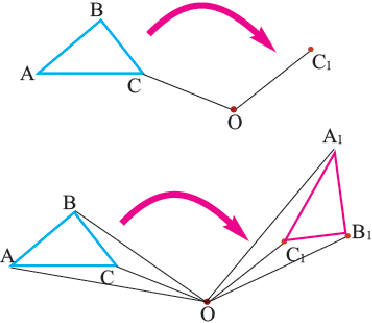
Пример 2. Проанализируйте последовательность шагов, при котором совершается поворот треугольника 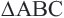
- 1. Соедините точку О и точку С отрезком прямой.
- 2. При помощи транспортира от ОС постройте угол 120° в направлении по часовой стрелке и циркулем отложите отрезок
, конгруэнтный отрезку ОС.
- 3. Потому же правилу соедините точку О с точками А и В. Постройте отрезки
конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки
являются вершинами нового треугольника. Соедините эти точки.
Примечание. Центральная симметрия является поворотом плоскости относительно центра симметрии на 180°.
Исследуйте и начертите в тетради:
На рисунке показана последовательность шагов, которые выполняются при повороте треугольника 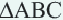
При повороте на угол 90″ в направлении по часовой стрелке координаты вершин изменяются следующим образом.
- Отношения, пропорция
- Пропорциональные отрезки
- Периметр подобных многоугольников
- Признаки подобия треугольников
- Подобие прямоугольных треугольников
- Применение подобия треугольников
- Высоты, медианы и биссектрисы подобных треугольников
- Свойство биссектрисы треугольника
- Теорема. Свойство медиан треугольника
- Преобразование подобия, гомотетия
- Площади подобных фигур
- Математика
- Презентация по геометрии «Подобие четырехугольников»
- «Управление общеобразовательной организацией: новые тенденции и современные технологии»
- Дистанционное обучение как современный формат преподавания
- Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Математика: теория и методика преподавания в образовательной организации
- Оставьте свой комментарий
- Подарочные сертификаты
- 📺 Видео
Видео:Как решить любую задачу с четырёхугольниками? | Математика TutorOnlineСкачать

Отношения, пропорция
Свойства пропорции
Если 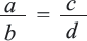
Если 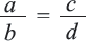
Если 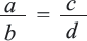
Если 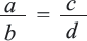
Видео:Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать

Пропорциональные отрезки
Практическая работа. Пропорциональные отрезки.
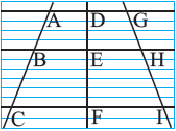
1. Начертите в тетради 3 параллельные прямые.
2. Проведите 3 секущие, которые пересекают эти прямые.
3. Измерьте отрезки АВ, ВС, AC, DE, EF, DF, GH, HI и GI.
4. Запишите и вычислите следующие отношения
5. Можно ли по результатам сказать, что параллельные линии делят секущие на пропорциональные отрезки? Пропорциональные отрезки
Если для отрезков АВ, CD, 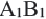
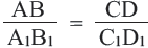
Теорема. Параллельные линии, пересекающие стороны угла, отсекают от них пропорциональные отрезки.
Доказательство. Допустим, что параллельные прямые пересекают стороны угла А в точках В и С, 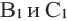
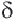
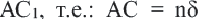
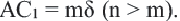
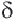
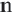
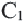
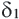
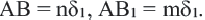
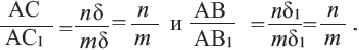
Подобные четырехугольники, подобные треугольники
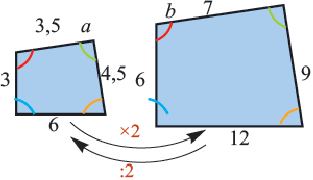
Подобными называются фигуры одинаковые по форме и у которых соответствующие размеры пропорциональны. Например, все квадраты подобны друг другу, так же как и окружности разных радиусов.
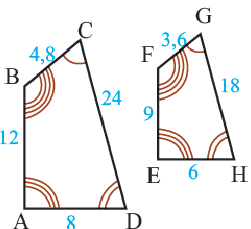
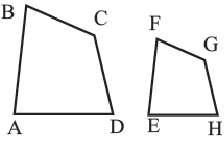
Подобными называются многоугольники, у которых соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Например, на рисунке четырёхугольники ABCD и EFGH являются подобными четырёхугольниками. Так как,
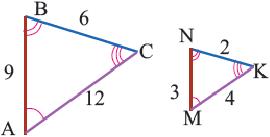
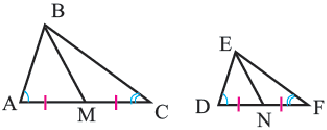
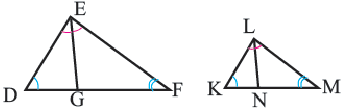
У подобных треугольников соответствующие углы конгруэнтны, а соответствующие стороны являются пропорциональными отрезками. Здесь, говоря о соответствующих сторонах, имеются в виду стороны, которые находятся напротив конгруэнтных углов. На рисунке для 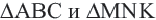
Так как 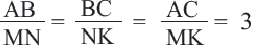
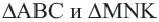
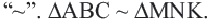
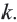
Видео:Подобие треугольников. Признаки подобия треугольников (часть 1) | МатематикаСкачать

Периметр подобных многоугольников
Теорема. Отношение периметров двух подобных многоугольников равно отношению соответствующих сторон (или коэффициенту подобия)
Если 
Запишите доказательство теоремы, приняв коэффициент подобия за 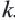
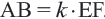
Видео:Как ПОНЯТЬ ГЕОМЕТРИЮ за 5 минут — Подобие ТреугольниковСкачать

Признаки подобия треугольников
Признак подобия УУ (угол угол)
Если два угла одного треугольника конгруэнтны двум углам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как УУ.
Признак подобия ССС
Если три стороны одного треугольника соответственно пропорциональны трём сторонам другого треугольника, то такие треугольники подобны. Этот признак подобия коротко записывается как ССС.
Признак подобия СУС
Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами конгруэнтны, то такие треугольники подобны. Этот признак подобия коротко записывается как СУС.
Видео:Параллелограмм, прямоугольник, ромб,квадрат,трапеция, все свойства и определения!!!Скачать

Подобие прямоугольных треугольников
Высота, проведенная к гипотенузе
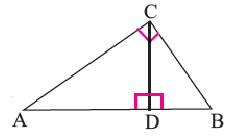
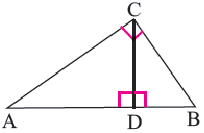
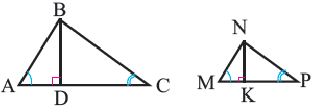
Теорема. Высота, проведённая из вершины прямого угла прямоугольного треугольника, делит его на два подобных треугольника, каждый из которых подобен данному треугольнику.
Доказательство данной теоремы проводится на основании признака подобия УУ Для каждого из трёх треугольников нужно определить два конгруэнтных угла.
Среднее геометрическое
Среднее геометрическое. Для положительных чисел а и b средним геометрическим называется положительное число 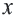
Высота, проведённая из вершины прямого угла на гипотенузу, делит её на два отрезка (на рисунке AD и DB) Здесь отрезки AD и DB являются проекциями катетов АС и ВС на гипотенузу, соответственно.
Следствие 1. Высота прямоугольного треугольника, опущенная из вершины прямого угла есть среднее геометрическое отрезков, на которые она делит гипотенузу.
Следствие 2. Каждый катет прямоугольного треугольника есть среднее геометрическое между гипотенузой и проекцией этого катета на гипотенузу.
Видео:Миникурс по геометрии. ЧетырехугольникиСкачать

Применение подобия треугольников
Пропорциональные отрезки
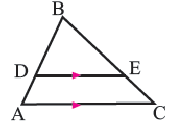
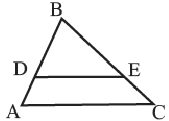
Теорема. Прямая, пересекающая две стороны треугольника, и параллельная третьей стороне делит стороны на пропорциональные отрезки.
Если
Обратная теорема. Если прямая, пересекающая две стороны треугольника делит их на пропорциональные отрезки, то эта прямая параллельна третьей стороне.
Если 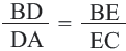
Видео:8 класс, 22 урок, Первый признак подобия треугольниковСкачать

Высоты, медианы и биссектрисы подобных треугольников
Теорема 1. Если два треугольника подобны, то отношение длин соответствующих высот равны отношению длин соответствующих сторон.
Теорема 2. Если два треугольника подобны, то отношение длин соответствующих медиан равны отношению длин д соответствующих сторон.
Теорема 3. Если два треугольника подобны, то отношение длин соответствующих биссектрис равны отношению длин соответствующих сторон.
Свойство биссектрисы треугольника
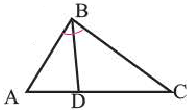
Теорема. Биссектриса треугольника делит противоположную сторону на отрезки пропорциональные двум другим сторонам.
Теорема. Свойство медиан треугольника
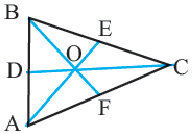
Медианы треугольника пересекаются в одной точке и делятся в точке пересечения в отношении 2:1, начиная от вершины.
Точка пересечения медиан называется центром тяжести треугольника.
Доказательство теоремы представлено в виде двухстолбчатой таблицы.
Дано: 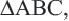
Доказательство: соединим точки O и E.
Видео:Вписанные и описанные четырехугольники. Практическая часть. 9 класс.Скачать

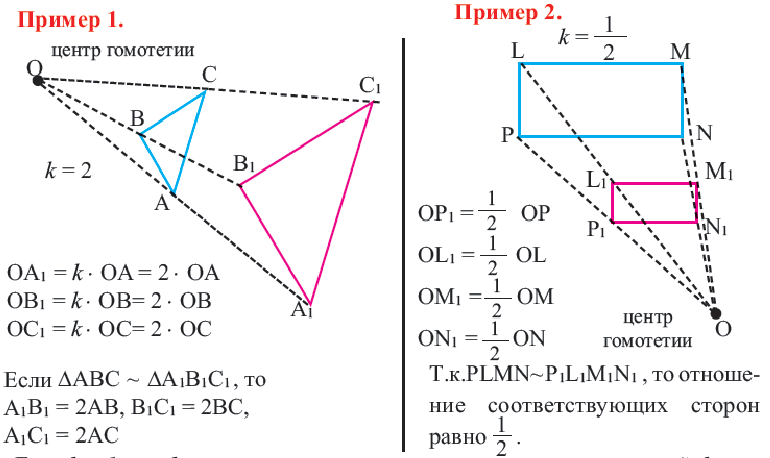
Преобразование подобия, гомотетия
Гомотетия
Преобразование плоскости на себя, при котором расстояние между любыми двумя точками изменяется в одно и то же число раз называется преобразованием подобия. Фигуры называются подобными, если одна фигура переводится в другую преобразованием подобия. Если при преобразовании подобия точки А и В на плоскости соответственно преобразованы в точки 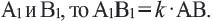
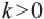
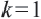
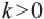
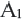
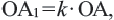
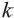
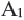
Если 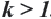
Если 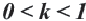
Если 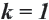
Площади подобных фигур
Теорема. Отношение площадей подобных фигур равно квадрату коэффициента подобия. Например, если отношение соответствующих сторон двух подобных четырёхугольников равно 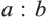
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Многоугольник
- Площадь многоугольника
- Правильные многоугольники
- Вписанные и описанные многоугольники
- Четырехугольник
- Площади фигур в геометрии
- Площади поверхностей геометрических тел
- Вычисление площадей плоских фигур
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:8 класс, 3 урок, ЧетырехугольникСкачать

Математика
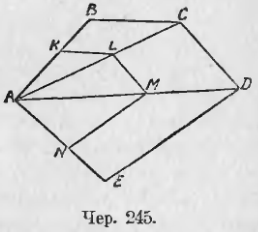
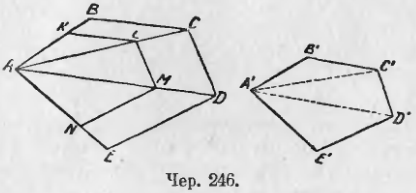
252. Понятие о подобии треугольников распространяется и на многоугольники. Пусть дан многоугольник ABCDE (чер. 245); выполним построение аналогичное п. 206. Построим диагонали AC и AD и, выбрав какую-либо точку K на стороне AB между точками A и B или вне отрезка AB, построим KL || BC до пересечения с диагональю AC, затем LM || CD до пересечения с AD и, наконец, MN || DE до пересечения с AE. Тогда получится многоугольник AKLMN, который связан с ABCD следующими зависимостями:
1) Углы одного многоугольника равны попарно углам другого: угол A у них общий, ∠K = ∠B (как соответственные), ∠KLM = ∠BCD, ибо ∠KLA = ∠BCA и ∠ALM = ∠ACD и т. д.
2) Сходственные стороны этих многоугольников пропорциональны, т. е. отношение одной пары сходственных сторон равно отношению другой пары, равно отношению третьей пары и т. д.
«Сходственные» стороны здесь надо понимать несколько иначе, чем для треугольников: здесь считаем сходственными сторонами те, которые заключены между равными углами, например, BC и KL.
Справедливость указанной пропорциональности видна следующим образом:
∆ABC, следовательно, AK/AB = KL/BC = AL/AC
∆ALM
∆ACD, следовательно, AL/AC = LM/CD = AM/AD
∆AMN
∆ADE, следовательно, AM/AD = MN/DE = AN/AE
Мы видим, что среди первых трех равных отношений и среди вторых трех равных отношений имеется одно одинаковое AL/AC; также и последние три отношения связываются с предыдущими отношением AM/AD. Поэтому, пропуская отношения диагоналей, получим:
AK/AB = KL/BC = LM/CD = MN/DE = AN/AE
Все это остается, как легко видеть, справедливым и для многоугольника с большим, чем у нас, числом сторон.
Если мы многоугольник AKLMN перенесем в другое место плоскости, то найденные выше 2 соотношения этого многоугольника с ABCDE останутся в силе; такие многоугольники называются подобными. Итак, два многоугольника называются подобными, если углы одного равны попарно углам другого и если сходственные стороны их пропорциональны .
Мы, следовательно, умеем строить многоугольник, подобный данному. Мы построили AKLMN
Мы видим еще, что в многоугольниках ABCDE и AKLMN построены диагонали из их соответственных вершин,причем получилось два ряда подобных треугольников: ∆AKL
∆ADE — треугольники эти одинаково расположены в обоих многоугольниках.
Возникает вопрос, останется ли в силе последнее свойство, если мы построим многоугольник, подобный данному, каким-либо еще способом, не тем, которым мы пользовались здесь.
253. Пусть как-либо построен многоугольник A’B’C’D’E’ подобный многоугольнику ABCDE (чер. 246), т. е. так, что
∠A’ = ∠A, ∠B’ = ∠B, ∠C’ = ∠C, ∠D’ = ∠D, ∠E’ = ∠E (1)
A’B’/AB = B’C’/BC = C’D’/CD = D’E’/DE = E’A’/EA (2)
Вопрос конца предыдущего п. равносилен другому: можно ли привести эти два многоугольника в положение, чтобы, например, точка A’ совпала с A, а остальные вершины были бы расположены попарно на прямых, идущих из этой общей точки, и чтобы сходственные стороны их или были параллельны, или сторона одного многоугольника расположилась бы на стороне другого.
Решим этот вопрос. Для этого отложим на стороне AB от точки A отрезок AK = A’B’ и, пользуясь предыдущим п., построим многоугольник AKLMN
Остается выяснить, может ли многоугольник A’B’C’D’E’ совпасть при наложении с AKLMN.
Мы имеем: AK/AB = KL/BC = LM/CD = MN/DE = NA/EA.
Сравнивая эти равенства с равенствами (2) и принимая во внимание, что AK = A’B’, легко получаем KL = B’C’, LM = C’D’ и т. д., т. е. все стороны многоугольников A’B’C’D’E’ и AKLMN попарно равны. Наложим многоугольник A’B’C’D’E’ на AKLMN так, чтобы A’ попала в A и сторона A’B’ совпала бы с AK (мы ведь строили AK = A’B’); тогда, в силу равенства углов B’ и K, сторона B’C’ пойдет по KL, в силу равенства сторон KL и B’C’, точка C’ попадет в L и т. д.
Итак, A’B’C’D’E’ совпадает с AKLMN, а следовательно, если построим диагонали A’C’ и A’D’, получим ряд треугольников, подобных и одинаково расположенных с ∆ABC, ∆ACD и т. д.
Поэтому заключаем: Если построить в подобных многоугольниках диагонали из соответственных вершин, то получим 2 ряда подобных и одинаково расположенных треугольников.
Легко увидать справедливость и обратного заключения: если, ∆A’B’C’
∆ADE, то многоугольник A’B’C’D’E’
многоугольнику ABCDE. Тогда ∆A’B’C’ = ∆AKL, ∆A’C’D’ = ∆ALM и ∆A’D’E’ = ∆AMN, откуда следует равенство многоугольников A’B’C’D’E’ и AKLMN и, следовательно, подобие A’B’C’D’E’ и ABCDE.
254. То положение (две соответственных вершины сливаются в одной точке, остальные вершины попарно лежат на прямых, проходящих чрез эту точку, а сходственные стороны параллельны), в которое нам удалось привести два подобных многоугольника, является частным случаем другого более общего положения двух подобных многоугольников.
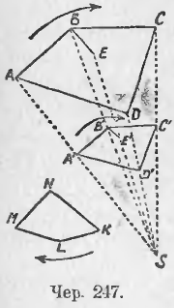
Пусть имеем KLMN
ABCD (чер. 247). Возьмем какую-либо точку S и соединим ее со всеми вершинами A, B, C и D первого многоугольника. Постараемся построить многоугольник, равный многоугольнику KLMN, так, чтобы его вершины лежали на прямых SA, SB, SC и SD и стороны были бы параллельны сторонам многоугольника ABCD.
Для этого отложим на стороне AB отрезок AP = KL (полагаем, что KL и AB сходственные стороны) и построим PB’ || AS (на чертеже точка P и прямая PB’ не даны). Чрез точку B’, где SB пересекается с PB’, построим B’A’ || AB. Тогда A’B’ = AP = KL, затем построим B’C’ || BC, чрез точку C’, где B’C’ пересекается с SC, проведем C’D’ || CD и точку D’, где C’D’ пересекается с SD, соединим с A’. Получим многоугольник A’B’C’D’, который, как это сейчас увидим, подобен многоугольнику ABCD.
Так как A’B’ || AB, то ∆SA’B’
SA’/SA = A’B’/AB = SB’/SB (1)
Так как B’C’ || BC, то ∆SB’C’
SB’/SB = B’C’/BC = SC’/SC (2)
Так как C’D’ || CD, то ∆SC’D’
SC’/SC = C’D’/CD = SD’/SD (3)
Отсюда можно вывести, что SA’/SA = SD’/SD, а следовательно ∆SA’D’
∆SAD, так как две стороны одного пропорциональны двум сторонам другого и углы между ними равны (∠S общий), — A’D’ || AD и
SD’/SD = D’A’/DA = SA’/SA (4)
Из равенств отношений (1), (2), (3) и (4) легко получаем:
A’B’/AB = B’C’/BC = C’D’/CD = D’A’/DA (5)
Кроме того, ∠A’ = ∠A, ∠B’ = ∠B и т. д., как углы с параллельными сторонами. Следовательно, A’B’C’D’
Далее легко увидать, что KLMN = A’B’C’D’. В самом деле, ∠K = ∠A, но ∠A = ∠A’, следовательно, ∠K = ∠A’; также ∠L = ∠B’ и т. д. — углы у наших многоугольников равны. Креме того, из подобия KLMN
KL/AB = LM/BC = MN/CD = NK/DA.
Сравнивая эти равные отношения с равенствами (5) и имея в виду, что A’B’ = KL, находим: B’C’ = LM, C’D’ = MN, D’A’ = NK. Теперь легко, как это делали выше, увидать, что KLMN при наложении совместится с A’B’C’D’. Следовательно, нам удалось поместить данные подобные многоугольники в такое положение, что их вершины расположены попарно на прямых, проходящих чрез точку S и их сходственные стороны параллельны, к чему мы и стремились.
Заметим еще, что соответственные вершины в наших многоугольниках следуют друг за другом в одном направлении (см. стрелки около многоугольников ABCD, KLMN и A’B’C’D’) — по часовой стрелке.
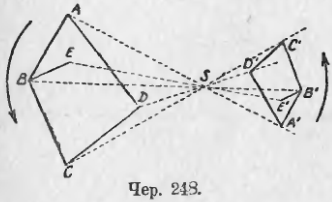
Если бы вершины одного многоугольника, соответствующие последовательным вершинам другого, шли друг за другом в направлении, обратном тому, как они расположены в другом, то удалось бы поместить наши многоугольники так, чтобы соответствующие вершины располагались по разные стороны от точки S (см. чер. 248).
Точка S, где сходятся прямые, соединяющие пары соответственных вершин многоугольников, называется центром подобия; в первом случае (чер. 247), когда обе соответственные вершины (например, A и A’) расположены в одной стороне от S, центр подобия называется внешним , а во втором (чер. 248), когда соответствующие вершины расположены по разные стороны точки S, центр подобия называется внутренним . Если подобные многоугольники расположены так, что они имеют центр подобия, то говорят, что они подобно расположены .
255. Если нам дан многоугольник ABCD (чер. 247 или 248), — будем данный многоугольник называть оригиналом , — мы можем, выбрав произвольную точку S, получать его изображения, подобные ему в каком угодно масштабе , — этим именем называют отношение какого-либо отрезка изображения к соответствующему отрезку в оригинале (в данном многоугольнике). Это отношение называют еще коэффициентом подобия — обозначим его через k. Пока еще для нас коэффициентом подобия является отношение стороны изображения к стороне оригинала, т. е.
A’B/AB = B’C/BC = … = k.
В дальнейшем мы распространим это понятие на отношение всяких двух отрезков изображения и оригинала, сходственных между собою.
Из равенства (1), (2), (3) и (4) предыдущего п., имеем:
SA’/SA = SB’/SB = SC’/SC = SD’/SD = A’B’/AB = k,
т. е. отношение расстояний от центра подобия соответственных вершин изображения и оригинала = коэффициенту подобия.
Под именем фигура (плоская) мы понимаем совокупность точек и линий плоскостей. Многоугольники ABCD — есть фигура. Присоединим еще одну точку (выбранную по произволу) E — получим новую фигуру состоящую из многоугольника ABCD и точки E, — найдем изображение точки E. Для этого построим прямую SE и на ней отложим отрезок SE так, чтобы SE’/SE = k (такой отрезок легко построить, пользуясь п. 214); этот отрезок мы можем отложить по направлению SE (чер. 247); или в обратном направлении (чер. 248). Полученная точка E’ и есть изображение точки E — другими словами точки E’ и E суть соответственные точки в наших двух подобных и подобно расположенных фигурах.
Соединив точку E, например, с B и точку E’ с B’ (B и B’ суть тоже соответственные точки), получим два соответствующих друг другу отрезка BE и B’E’.
Легко увидать, что ∆SBE
∆SB’E’ (так как ∠BSE = ∠B’SE и стороны, составляющие эти углы, пропорциональны: SB’/SB = k и SE’/SE = k, — следовательно, SB’/SB = SE’/SE), отсюда вытекает:
1) B’E’ || BE и 2) B’E’/BE = SB’/SB = k
т. е. соответствующие друг другу отрезки в изображении и оригинале 1) параллельны между собою и 2) их отношение равно коэффициенту подобия .
Отсюда вытекает возможность следующего построения для нахождения точки, соответствующей данной в оригинале точке, если уже имеем одну пару соответствующих точек и известен центр подобия: пусть имеем пару соответствующих точек B и B’ и требуется найти точку, соответствующую точке E, — строим прямые SE и BE и чрез B’ строим прямую, параллельную BE, ее точка пересечения E’ с SE и даст искомую точку.
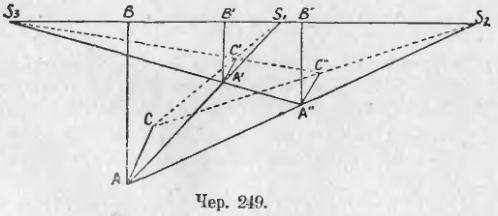
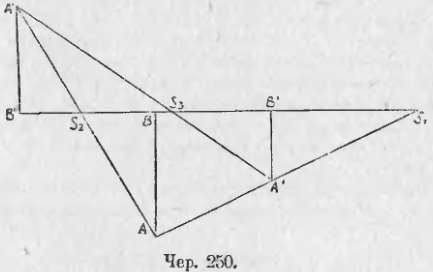
256. Построим для какой-либо фигуры, одна точка которой есть A (чер. 249), ее изображения, принимая две произвольных точки S1 и S2 за внешние центры подобия и числа k1 и k2 за коэффициенты подобия. Пусть в первом изображении точке A соответствует точка A’ и во втором изображении этой же точке соответствует точка A».
Присоединим еще к данной фигуре какую-либо точку B, лежащую на прямой S1S2; тогда этой точке B соответствуют в первом изображении точка B’ и во втором точка B», причем точки B’ и B» должны лежать на той же прямой S1S2 и прямые AB, A’B’ и A»B» должны быть параллельны и одинаково направлены.
Соединим точки A’ и A», найдем точку пересечения S3 прямых A»A’ и S2S1. Тогда из подобия треугольников S3A’B’ и S2A»B» находим:
Соединив точки A’ и A», найдем точку пересечения S3 прямых A»A’ и S2S1. Тогда из подобия треугольников S3A’B’ и S2A»B» находим:
т. е. точка S2 должна делить отрезок B’B» внешним образом в отношении, равном данному числу k1/k2. Мы знаем (п. 217), что существует только одна точка, которая делит данный отрезок B’B» в данном отношении внешним образом. Если мы возьмем какую-либо еще точку C данной фигуры и построим ее изображения C’ и C», то, соединив точки C’ и C» и взяв точку пересечения, назовем ее опять S3, прямой C’C» с прямой S1S2, получим, что ∆S3B’C’
∆S3B»C» (B»C» || BC и B’C’ || BC, следовательно, B»C» || B’C’), откуда опять найдем, что S3B’/S3B» = k1/k2, т. е. новая точка S3 совпадает с прежнею. Следовательно, S3 есть центр подобия фигур (A’B’C’. ) и (A»B»C». ) и притом внешний, ибо направления, в котором следуют друг за другом соответствующие точки в обеих фигурах, одинаковы. Из этого заключаем, что фигуры (A’B’C’. ) и (A»B»C». ) также имеют внешний центр подобия и он расположен на одной прямой с центрами S1 и S2.
Если одни из центров подобия S1 взять внешний, а другой S2 внутренний (чер. 250), то направления соответствующих отрезков таковы: A’B’ одинаково с направлением AB, но A»B» обратно направлению AB, — следовательно, направление A»B» обратно A’B’ и S3 является внутренним центром подобия фигур (A’B’. ) и (A»B». ).
Если взять оба центра подобия внутренними (например, S2 и S3 на чер. 250), то легко увидать, что третий центр подобия окажется внешним. Итак, вообще:
Если три фигуры попарно подобно расположены, то три центра подобия расположены на одной прямой, причем или все три они внешние, или два из них внутренних, а один внешний.
257. Отношение периметров и площадей подобных многоугольников.
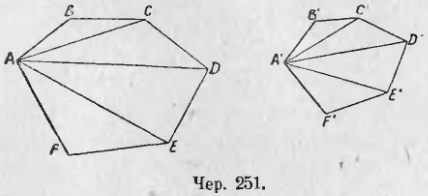
Пусть имеем два подобных многоугольника ABCDEF и A’B’C’D’E’F’ (чер. 251). Назовем коэффициент подобия чрез k.
A’B’/AB = k, B’C’/BC = k и т. д.,
A’B’ = k · AB, B’C’ = k · BC, C’D’ = k · CD, …
Сложив эти равенства по частям и вынеся множитель k во второй части за скобку, получим:
A’B’ + B’C’ + C’D’ + … = k(AB + BC + CD + …),
(A’B’ + B’C’ + C’D’ …) / (AB + BC + CD + …) = k = A’B’/AB,
т. е. отношение периметров подобных треугольников равно отношению сходственных сторон (или равно коэффициенту подобия).
Выберем две соответственных вершины, напр., A и A’, и построим проходящие чрез них диагонали. Тогда мы знаем: 1) (из п. 253) ∆ABC
∆A’C’D’ и т. д. 2) (из п. 212). Отношение площадей подобных треугольников равно квадрату отношения их сходственных сторон, следовательно,
пл. ∆A’B’C’ / пл. ∆ABC = (A’B’/AB) 2 = k 2 ; пл. ∆A’C’D’ / пл. ∆ACD = (C’D’/CD) 2 = k 2 и т. д.,
пл. ∆A’B’C’ = k 2 · пл. ∆ABC; пл. ∆A’C’D’ = k 2 · пл. ∆ACD;
пл. ∆A’D’E’ = k 2 · пл. ∆ADE .
Сложив эти равенства по частям и вынеся общего множителя k 2 во второй части за скобку получим:
пл. ∆A’B’C’ + пл. ∆A’C’D’ + ∆A’D’E’ + … = k 2 (пл. ∆ABC + пл. ∆ACD + пл. ∆ADE + …),
пл. A’B’C’D’E’F’ / пл. ABCDEF = k 2 = (A’B’/AB) 2 ,
т. е. отношение площадей подобных многоугольников равно квадрату отношения их сходственных сторон (или равно квадрату коэффициента подобия).
258. Два правильных одноименных многоугольника всегда подобны. В самом деле, углы у одноименных многоугольников одинаковы (п. 248), а так как все стороны каждого равны между собою, то, очевидно, отношение любой стороны одного к любой стороне другого есть число постоянное.
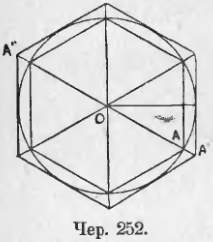
Если в круг впишем какой-либо правильный многоугольник (чер. 252) и чрез середины дуг, стягиваемых его сторонами, построим касательные к кругу, то получим правильный одноименный многоугольник, описанный около этого круга. Не трудно выяснить (предоставляем это желающим), что полученные два правильные многоугольника подобно расположены, и центр круга служит их внешним центром подобия, – внешним потому, что каждая пара соответствующих точек (напр., A и A’) расположена в одном направлении от центра (если многоугольник имеет четное число сторон, то центр круга можно считать и внутренним центром подобия, надо лишь считать, что, например, точке A соответствует точка A»).
259. Упражнения.
1. Стороны одного пятиугольника равны соответственно 12, 14, 10, 8 и 16 дм. Найти стороны другого пятиугольника, подобного первому, если его периметр = 80 дм.
2. Сумма площадей двух подобных многоугольников равна 250 кв. дм., а отношение двух сходственных сторон = ¾. Вычислить площадь каждого из них.
3. Показать, что если в круг вписан правильный многоугольник с нечетным числом сторон и в его вершинах построены касательные к кругу, то получится описанный многоугольник, подобно расположенный с вписанным, – центр круга служит их внутренним центром подобия.
4. Дан треугольник; построить другой треугольник, подобно расположенный с первым так, чтобы центр тяжести первого служил внутренним центом подобия и чтобы коэффициент подобия = ½. Выяснить при помощи этого, как расположены точки высот, центр тяжести и центр описанного круга данного треугольника.
5. В данный треугольник вписан квадрат.
Пусть ABC данный треугольник (чер. 253) и DEFK искомый квадрат. Построим еще квадрат MNPQ, чтобы одна сторона MQ лежала на стороне AC треугольника и точка N на стороне AB. Легко видеть, что квадрат MNPQ подобно расположен с искомым квадратом DEFK и внешним их центром подобия является точка A; следовательно, точка F лежит на прямой AP. После нахождения точки F искомый квадрат легко построить.
6. Дан угол и точка внутри его. Найти на одной стороне угла точку, равноудаленную от данной точки и от другой стороны.
Задача решается тем же приемом.
7. Построить треугольник по его высотам.
Легко получить, называя стороны треугольника чрез a, b и c и соответствующие высоты чрез ha, hb и hc, следующую зависимость:
Легко построить отрезок x = (hbha)/hc (x/ha = hb/hc — построение 4-го пропорционального), после чего построим треугольник со сторонами hb, ha и x. Этот треугольник подобен искомому, так как a : h : c = hb : ha : x; остается построить треугольник подобный только что построенному так, чтобы одна его высота была равна данной.
Видео:Классификация четырёхугольников (видео 58) | Подобие. Геометрия | МатематикаСкачать

Презентация по геометрии «Подобие четырехугольников»
Видео:Свойство и признак вписанного четырехугольникаСкачать

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Описание презентации по отдельным слайдам:
Признаки подобия четырехугольников средством математического эксперимента МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «Средняя школа №6 имени Героя Советского Союза А.С.Степина» г. Рославля Смоленской области Работу выполнили учащиеся 8 класса: Няйкина Евгения, Доронкина Екатерина Руководитель: Тихонова Людмила Георгиевна, учитель математики высшей категории Исследовательский проект по геометрии
Корбюзье французский архитектор “Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг – геометрия”
Содержание Введение Глава 1. Четырехугольники Из истории четырехугольников Четырехугольники в нашей жизни Глава 2. Преобразование подобия Глава 3. Признаки подобия четырехугольников Глава 4. Признак подобия четырехугольников по средствам математического эксперимента Заключение Список используемой литературы
Гипотеза Метод подобия широко применяется при решении геометрических задач. Однако в школьном курсе геометрии рассматриваются только три признака подобия треугольников, а признаки подобия четырехугольников и других выпуклых многоугольников не рассматриваются. А существуют ли таковы?
Цель проекта Вывести доказательства признаков подобия четырехугольников встречающихся в нашей жизни.
Задачи проекта Рассмотреть виды четырехугольников и рассмотреть где мы с ними сталкиваемся в жизни. Изучить преобразование подобия и метод математической индукции. Вывести признаки подобия четырехугольников. Применить признаки подобия четырехугольников по средствам математического эксперимента.
Методы и средства исследования При выведении признаков подобия различных видов четырехугольников использовала ранее изученные три признака подобия треугольников. При выведении признаков подобия четырехугольников использовала определение подобия; метод сведения задачи к рассмотрению треугольников и применение их признаков подобия. При доказательстве признака подобия произвольных выпуклых многоугольников, применяла метод математической индукции.
Признаки подобия четырехугольников 1. Все квадраты подобны. 2. Если угол одного ромба равен углу другого ромба, то такие ромбы подобны. 3. Если две соседние стороны одного прямоугольника пропорциональны двум сторонам другого прямоугольника, то такие прямоугольники подобны. В C1 B1 D А С D1 А1
5. Если угол одной трапеции равен углу другой трапеции, а стороны, образующие этот угол, и диагональ, выходящая из этого угла, соответственно пропорциональны двум сторонам другой трапеции, образующим угол, равный первому, и диагонали, выходящей из этого угла, то такие трапеции подобны. 4. Если соответственные стороны двух трапеций пропорциональны, то трапеции подобны. В С D А B1 C1 D1 А1 М1 М
Установление подобия граней спичечного коробка Измерения 50х35х12,5(мм)
Грани симметрии: 1)50х35 2)50х12,5 3) 35х12,5 1) 35 2) 12,5 3) 35 50 50 12,5 Будут ли подобны прямоугольники, образующие грани коробка? Первая и вторая грани подобны не будут т.к имеются одинаковые размеры сторон. Вторая и третья грани аналогично. Рассмотрим 1 и 3 грани . Установим пропорциональность сторон: 50*12,5=35*35 625=1225
Из неравенства следует, что данные грани не подобны. Вывод: Грани спичечного коробка не подобны
Исследование на подобие диагональных сечений двух этажей Эйфелевой башни
Нижний этаж представляет собой усеченную пирамиду (124,9м каждая сторона в основании). Образующая 4 колоннами, соединяющимися на высоте 57,63м. На своде покоится первая платформа Эйфелевой башни. Платформа представлена квадратом (65м в поперечнике).
Диагональное сечение первого этажа равнобедренная трапеция АВСD, где ВС — диагональ квадрата 1 платформы(ВС=65м). 1. АD- диагональ квадрата основания первого этажа. Найдем ее: Т D АD2=АО2+DО2 АD2=(124,9*124,9)+ +(124,9*124,9) АD2=√2124,9=124,9√2 АD= 176,64м
Сечение: 1)ВС=65 В С ВН=57,63м АD=2*(124,9*124,9) AD=176,63м АН=(176,63-65)/2= =55,8м А D Н М 2)АН=МD=(АD-НМ)/2 3)tg A=ВН/АН tg А=57,63/55,8=1,03 На платформу поднимается вторая пирамида – башня , образуется также 4 колонии, которые соединяются сводом, на котором находятся (на высоте 115,73м ) вторая платформа (квадрат в 35 м в поперечнике)
Сечение N K NК=35м МЕ=65м 1)NО=115,73-57,63=58,1м M E O F 2) МО=(МЕ-ОF)/2 МО=15м 3) tg β=NO/MO tg β=3,87 tg α≠ tg β
Вывод: Равнобедренные трапеции полученные в сечениях усеченных пирамид, являются двумя этажами Эйфелевой башни не являются подобными трапециями, так как не выполняется одно из условий подобия равнобедренных трапеций (равенство углов). Дальнейшие исследования по трапециям бесполезны.
Литература Александров А.Д., Вернер А.Л., Рыжик. Геометрия 8-9. Учебное пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1991. Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г. Планиметрия. Пособие для углубленного обучения математики. – М.: ФИЗМАТЛИТ, 2005. Мордкович А.Г., Семенов П.В. Алгебра и начала анализа. Учебник для общеобразовательных учреждений (профильный уровень). – М: Мнемозина, 2011. Прасолов В.В. Задачи по планиметрии. – М.: Наука, 1991; Шарыгин И.Ф.Геометрия 8 класс. Методическое пособие к учебнику. – М: Дрофа, 2000. Шарыгин И.Ф. Геометрия 7-9. Учебник по геометрии для общеобразовательных учебных заведений. – М.: Дрофа, 2001. Цукарь А.Я. Дидактические материалы по геометрии с элементами исследования. – М.: Просвещение, 1999.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 958 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 334 человека из 70 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 683 человека из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Тихонова Людмила ГеоргиевнаНаписать 1854 08.11.2020
Номер материала: ДБ-1471925
- 08.11.2020 0
- 08.11.2020 0
- 07.11.2020 0
- 07.11.2020 0
- 07.11.2020 0
- 07.11.2020 0
- 06.11.2020 0
- 06.11.2020 0
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор разрешил провести ВПР по некоторым предметам на компьютерах
Время чтения: 0 минут
Учительница из Киргизии победила в конкурсе Минпросвещения РФ «Учитель-международник»
Время чтения: 2 минуты
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Правительство направит регионам почти 92 миллиарда рублей на ремонт и оснащение школ
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
📺 Видео
Все про РОМБ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия 8 классСкачать

Описанные четырехугольники. 9 класс.Скачать
Четырехугольники, вписанные в окружность. 9 класс.Скачать

Четырехугольники. Вебинар | МатематикаСкачать

ЧЕТЫРЕХУГОЛЬНИКИ и их свойства+доказательство теорем/8 класс.Скачать

Свойства и признаки вписанного четырехугольникаСкачать

Вписанные четырехугольники. 9 класс.Скачать

Многоугольники. Математика 8 класс | TutorOnlineСкачать

Геометрия 8. Урок 4 - Прямоугольник, ромб, квадрат - свойства и признаки.Скачать

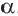
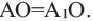
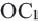 , конгруэнтный отрезку ОС.
, конгруэнтный отрезку ОС.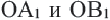 конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки
конгруэнтные полученным отрезкам OA и ОВ и составляющие с ними угол 120°. Точки 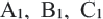 являются вершинами нового треугольника. Соедините эти точки.
являются вершинами нового треугольника. Соедините эти точки.